Complete Solutions to Integer Type Questions of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | Integer Type Questions |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
A ring and a disc having the same mass, roll without slipping with the same linear velocity. If the kinetic energy of the ring is 8 j , Find the kinetic energy of disc (in J)
View SolutionA wheel starting from rest is uniformly acceleration with angular acceleration of `4 "rad"//s^(2)` for 10 seconds . It is then allowed to rotate uniformly for next 10 seconds and finally brought to rest in next 10 seconds by uniform angular retardation. Total angle rotated is (100 n) radian. Find value of n.
View SolutionRadius of gyration of a body about an axis at a distance 6 cm from it COM is 10 cm . Its radius of gyration about a parallel axis passing through its COM is (n) cm . find value of n.
View SolutionA uniform rod of mass `2 kg` and length `1 m` lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of `2ms^-1` perpendicular to the length of the rod strikes it at a distance `(1)/(4)` m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
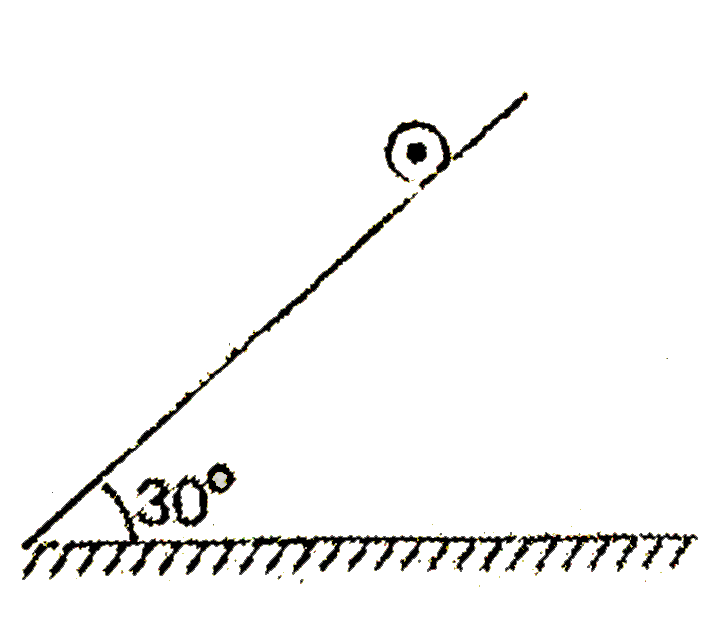
View SolutionAn uniform spherical shell of mass m and radius R starts from rest with pure rolling on long inclined plane as shown in figure. The angular momentum of shell about point of contact after 1 s of its starting is KmR. Determine the value of `k(g=10m//s^(2))`.
View SolutionA small pulley of radius 20 cm and moment of inertia `0.32 kg-m^(2)` is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition find the acceleration of the block ( in `m//s^(2)`).
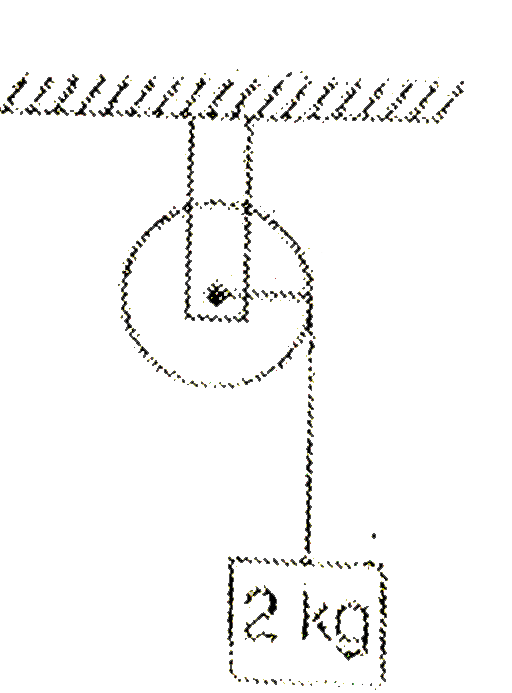
View SolutionIf a disc of mass m and radius r is reshaped into a ring a radius 2r,the mass remaining the same, the radius of gyration about centroidal axis perpendicular to plane goes up by a factor of `sqrt(x)` . Find the value of x.
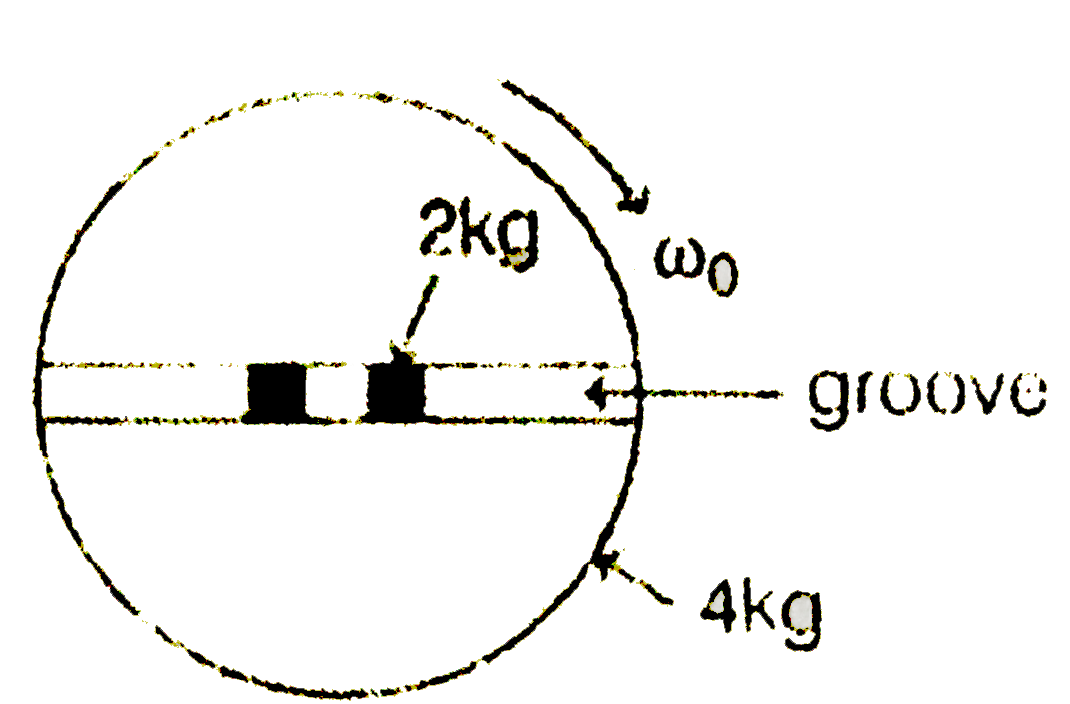
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity `omega_(0)` =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionFind the acceleration of slid right circular roller `A`, weighing `12kg` when it is being pulley by another weight `B (6 kg)` along the horizontal plane as in figure `(` pulley in massless `)`. The weight `B` is attached to the end of a string wound around the circularference of roller. Assume there is no slipping of the roller and the string is inextensible.

View SolutionTwo thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder

View SolutionA wheel of radius R=1 m rolls on ground with uniform velocity v=2 m/s . Calculate the relative acceleration of topmost point of wheel with respect to bottom most point (in `m//s^(2)`).
View SolutionA cylinder rolls down on an inclined plane of inclination `37^(@)` from rest. Coefficient of friction between plane and cylinder is 0.5. Calculate the time ( in s) of travelling down the incline 8 m as shown in figure .`(g=10 m//s^(2))`

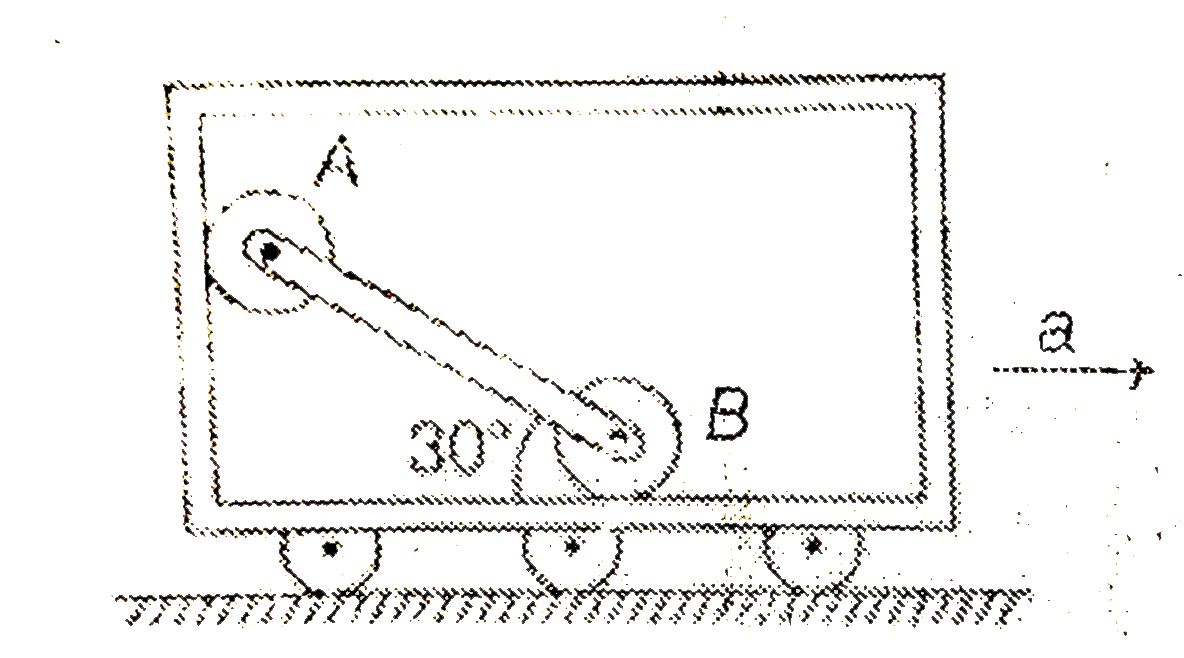
View SolutionA car is moving rightward with acceleration `a=gsqrt(k)m//s^(2)` . Find the value of k so that , rod maintains its orientation as shown in the figure. Neglect the friction and mass of the small rollers at A and B.
View SolutionA uniform thin rod has mass m and length l. One end of the rod lies over rough horizontal surface and the other end is connected to a light vertical string as shown in the figure. When string is cut, there is no slipping between rod and surface.Calculate the friction force (in N) on the rod immediately after the string is cut .(Given ` mg=(16)/(sqrt(3))N`)

View SolutionA wheel of radius R=2m performs pure rolling on a rough horizontal surface with speed v=10 m/s . In the figure shown, angle `theta` is angular position of point P on wheel reaches the maximum height from ground. Find the value of `"sec"theta` (take `g=10 m//s^(2)`).
View SolutionA uniform rod of length l and mass m is suspended from one end by inextensible string and other end less lies on smooth ground. The angle made by the rod with vertical is `theta="sin"^(-1)(1//sqrt(3))`. If `N_(1)` and `N_(2)` represent the contact force from ground on rod just before and just after cutting the string then the ratio of `N_(1)//N_(2)` is 0.25 x. Find the value of x.

View Solution
Integer Type Questions questions and complete solutions for chapter ROTATIONAL MOTION of DC PANDEY ENGLISH of Class 11