Complete Solutions to Example of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| DC PANDEY | Example |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Relative density of an oil is `0.8`.Find the absolute density of oil in CGS and SI units.
View SolutionFor the arrangement shown in the figure, what is the density of oil?
 .
.
View SolutionA U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury. Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with `h_(2)=1.0cm`, determine the value of `h_(1)`
 .
.
View SolutionA U-shaped tube open to the air at both ends contains some mercury. A quantity of water is carefully poured into the left arm of the U-shaped tube until the vertical height of the water column is `15.0 cm`.
(a) What is the gauge pressure at the water mercury interface ?
(b) Calculate the vertical distance h from the top of the mercury in the right hand arm of the tube to the top of the water in the left-hand arm.
 .
.
View SolutionFor the system shown in figure, the cylinder on the left, at L, has a mass of 600 kg and a cross-sectional area of `800 cm^(2)`. The piston on the right, at S, has cross-sectional area `25 cm^(2)` and negligible weight. If the apparatus is filled with oil `(rho=0.78 g//cm^(3))`, what is the force F required to hold the system is equilibrium?
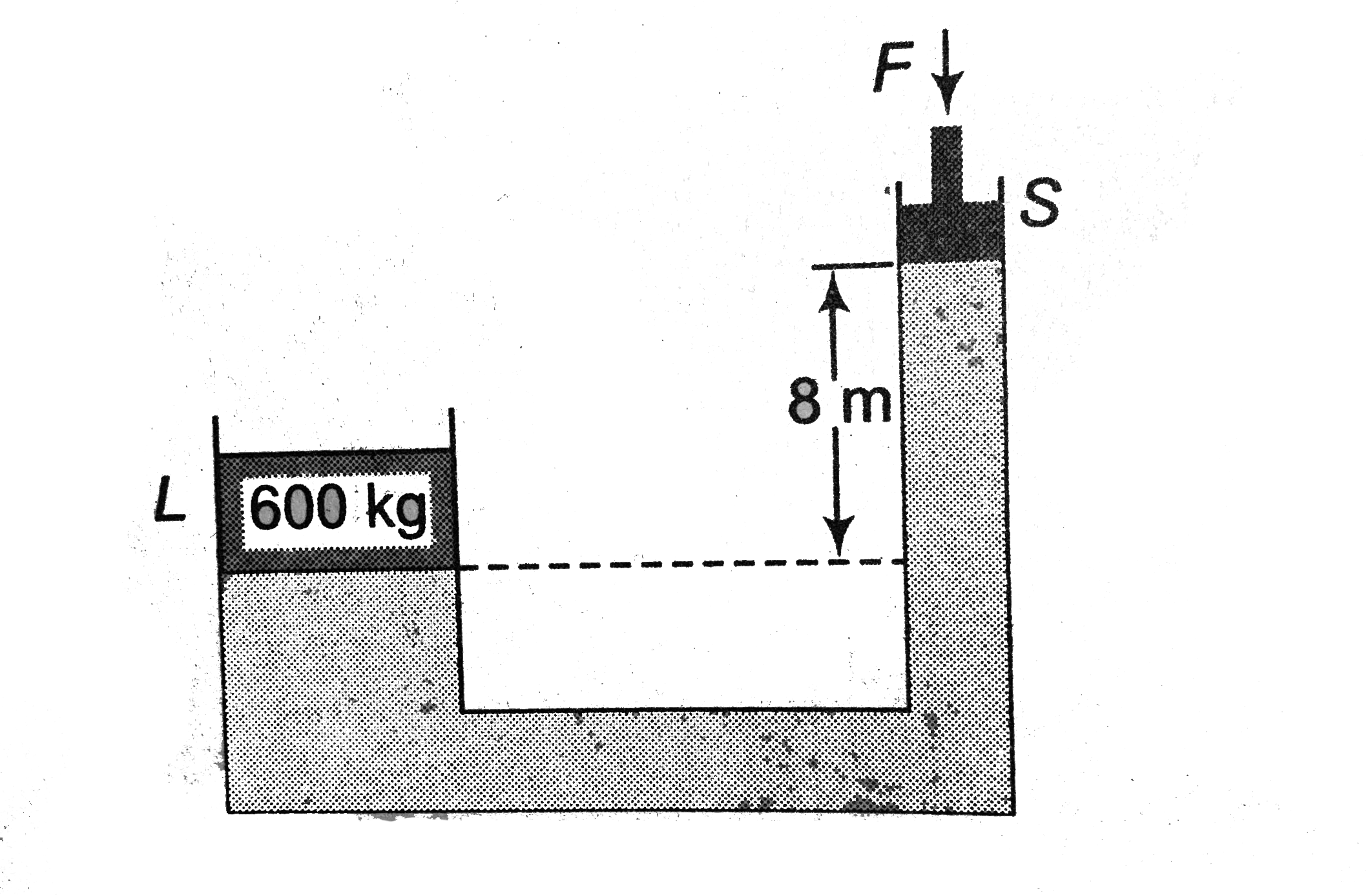 .
.
View SolutionA closed container shown in figure is filled with water `(rho=10^(3) kg//M^(3))`

This is accelerated in horizonal direction with an acceleration, `a=2m//s^(2)`.Find (a)`p_(C)-p_(D)` and (b) `p_(A)-p_(D)`.
View SolutionA closed tube is filled with

`AB=2m`
`BC=4cm`
water `(rho=10^(3)kg//m^(3))`. It rotating about an axis shown in figure with an angular velocity `omega=2 rad//s`. Find, `p_(A)-p_(C)`.
View SolutionA liquid of density `rho` is in a bucket that spins with angular velocity `'omega'` as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
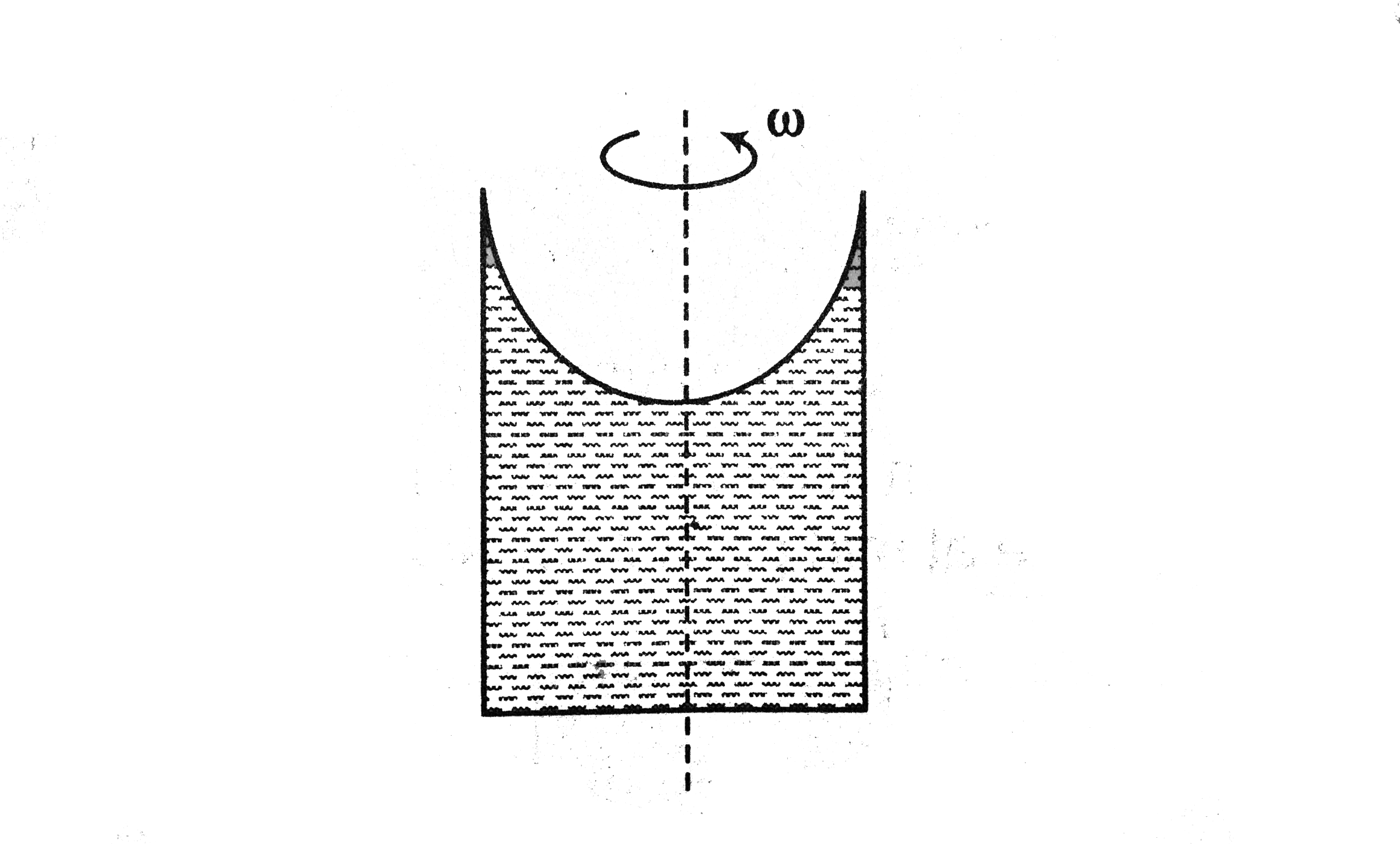 .
.
View SolutionDensity of ice is `900 kg//m^(3)`. A piece of ice is floating in water of density `1000kg//m^(3)`. Find the fraction of volume of the picec of ice outside the water.
View SolutionA metallic sphere floats in an immiscible mixture of water `(rho_(w)=10^(3)kg//m^(3))` and a liquid `(rho_(L)=13.5xx10^(3)kg//m^(3))` such that its `(4)/(5)th` volume is in water and `(1)/(5)th` volume in the liquid. Find the density of metal.
View SolutionA block of mass 1 kg and density `0.8g//cm^(3)` is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a `=1.0m//s^(2)`. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take `g=10m//s^(2)` and density of water `=10^(3)kg//m^(3))`.
View SolutionThe tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in figure is `T_(0)` when the system is at rest. What will be the tension in the string if the system has an upward acceleration a?
 .
.
View SolutionWater is flowing through a horizontal tube of non-uniform cross-section. At a place the radius of the tube is 1.0 cm and the velocity of water is `2 ms^(-1)`. What will be the velocity of water where the radius of the pipe is 2.0 cm ?
View SolutionCalculate the rate of flow of glycerine of density `1.25xx10^(3) kgm^(-3)` through the conical section of a horizontal pipe, if the radii of its ends are 0.1 m and 0.04 m and the pressure drop across its length is `10 Nm^(-2)`.
View SolutionWater is flowing smoothly through a closed-pipe system. At one point the speed of the water is `3.0m//s`. While at another point `1.0m` higher the speed is `4.0m//s`. If the pressure is `20 Kpa` at the lower point, what is the pressure at the upper point? What would the pressure at the upper point be if the water were to stop flowing and the pressure at the lower point were `18 kpa`?
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of height of water column in the vertical tubes in `2cm` and the areas of corss-section at A and B are `4 cm^(2)` and `2 cm^(2)` respectively. Find the rate of flow of water across any section.
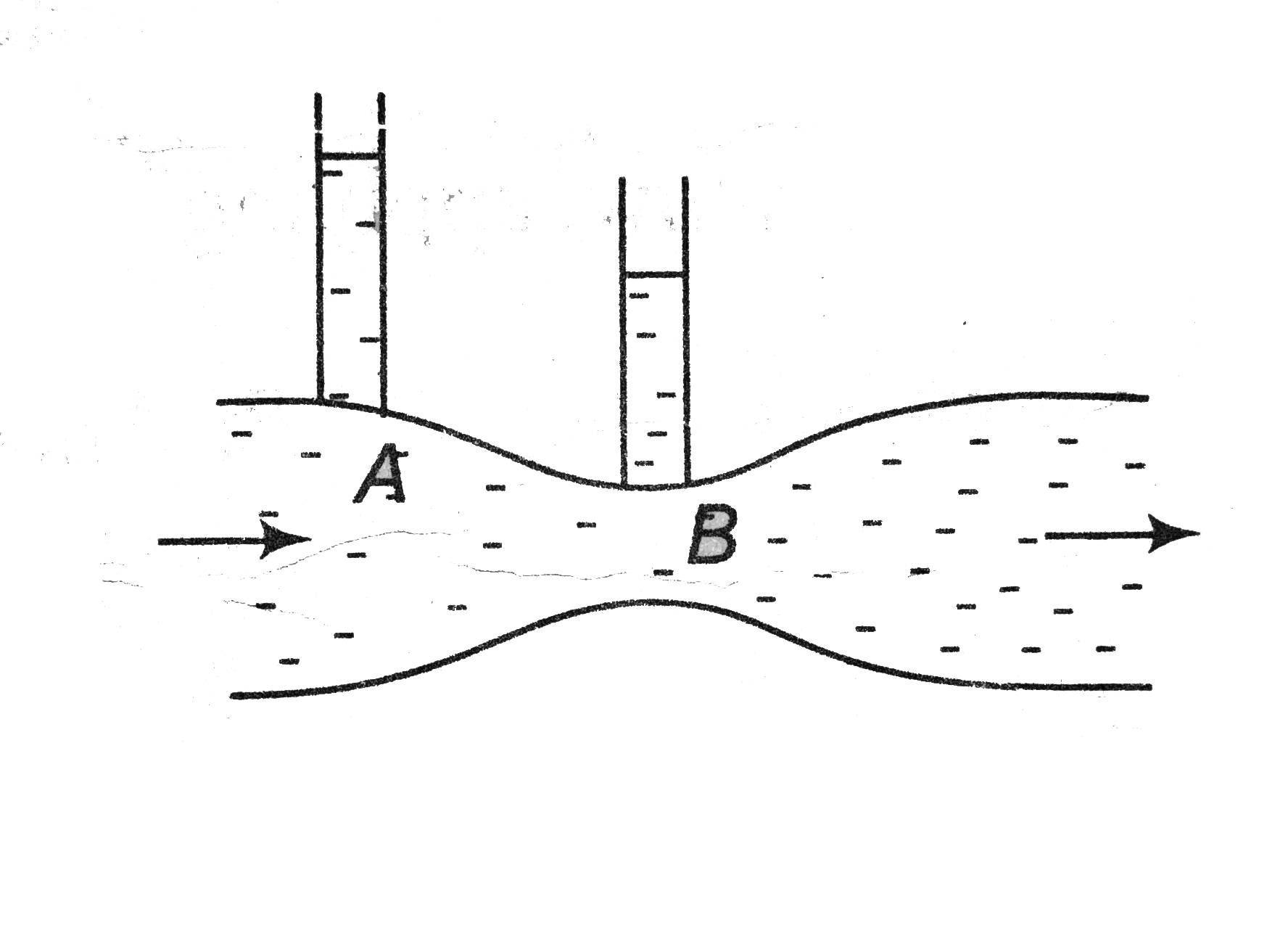 .
.
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are `5cm^2 and 2cm^2` respectively. The rate of flow of water through the tube is `500 cm^3s^-1` . Find the difference of mercury levels in the U-tube.

View SolutionA tank is filled with a liquid upto a height H, A small hole is made at the bottom of this tank Let `t_(1)` be the time taken to empty first half of the tank and `t_(2)` time taken to empty rest half of the tank then find `(t_(1))/(t_(2))`
View SolutionA plate of area `2m^(2)` is made to move horizontally with a speed of `2m//s` by applying a horizontal tangential force over the free surface of a liquid. If the depth of the liquid is 1m and the liquid in contact with the bed is stationary. Coefficient of viscosity of liquid is `0.01` poise. Find the tangential force needed to move the plate.
View SolutionTwo spherical raindrops of equal size are falling vertically through air with a velocity of `1 m//s`. What would be the terminal speed if these two drops were to coalesce to form a large spherical drop?
View SolutionWith what terminal velocity will an air bubble `0.8 mm` in diameter rise in a liquid of viscosity `0.15 N-s//m^(2)` and specific gravity `0.9`? Density of air is `1.293 kg//m^(3)`.
View SolutionA spherical ball of radius `3.0xx10^(-4) m` and density `10^(4) kg//m^(3)` falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h. Viscosity of water is `9.8xx10^(6) N-s//m^(2)`.
View SolutionA small sphere falls from rest in a viscous liquid. Due to friction, heat is produced. Find the relation between the rate of produced heat and the radius of the sphere at terminal velocity.
View SolutionHow much work will be done in increasing the diameter of a soap bubble from 2cm to 5cm? Surface tension solution is `3.0xx10^(-2)N//m.`
View SolutionCalculate the energy released when 1000 small water drops each of same radius `10^(-7)m` coalesce to form one large drop. The surface tension of water is `7.0xx10^(-2)N//m`.
View SolutionWhat should be the pressure inside a small air bubble of `0.1mm` radius situated just below the water surface. Surface tension of water `=7.2xx10^(-2)N//m` and atmosphere pressure`=1.013xx10^(5)N//m^(2)`.
View SolutionTwo separate air bubbles (radii `0.002 cm` and `0.004`) formed of the same liquid (surface tension `0.07 N//m`) come together to form a double bubble. Find the radius and the sense of curvature of the internal film surface common to both the bubbles.
View SolutionUnder isothermal condition two soap bubbles of radii `r_(1)` and `r_(2)` coalesce to form a single bubble of radius r. The external pressure is `p_(0)`. Find the surface tension of the soap in terms of the given parameters.
View SolutionAssume that a drop of liquid evaporates by decreases in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is `rho` and L is its latent heat of vaporization.
View SolutionA capillary tube whose inside radius is `0.5mm` is dipped in water having surface tension `7.0xx10^(-2) N//m`. To what height is the water raised above the normal water level? Angle of contact of water with glass is `0^(@)`. Density of water is `10^(3)kg//m^(3) and g=9.8 m//s^(2)`.
View SolutionA glass tube of radius `0.4mm` is dipped vertically in water. Find upto what height the water will rise in the capillary? If the tube in inclined at an angle of `60^(@)` with the vertical, how much length of the capillary is occupied by water? Suface of water`=7.0xx10^(-2)N//m`,density of water `=10^(3)kg//m^(3)`.
View SolutionMercury has an angle of contact of `120^(@)` with glass. A narrow tube of radius `1.0mm` made of the glass is dipped in a through containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside. Surface tension of mercury at the temperature of the experiment os `0.5 N//m` and density of mercury is `13.6xx10^(3) kg//m^(3)`.
(Take `g = 9.8 m//s^(2))`.
View SolutionIf a `5 cm` long capillary tube with `0.1 mm` internal diameter, open at both ends, is slightly dipped in water having surface tension `75 dyn//cm`, state whether:
(i) water will rise halfway in the capillary,
(ii) water will rise up to the upper end of capillary,
(iii) water will overflow out of the upper end of capillary.
Explain your answer.
View Solution
Example questions and complete solutions for chapter FLUID MECHANICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS FLUID MECHANICS
- Assertion and Reason
- B) Medical entrance special format question
- Check point 13.1
- Check point 13.2
- Check point 13.3
- Check point 13.4
- Example
- Example 13.1
- Example 13.10
- Example 13.11
- Example 13.12
- Example 13.13
- Example 13.14
- Example 13.15
- Example 13.16
- Example 13.17
- Example 13.18
- Example 13.19
- Example 13.2
- Example 13.20
- Example 13.21
- Example 13.22
- Example 13.23
- Example 13.24
- Example 13.25
- Example 13.26
- Example 13.27
- Example 13.28
- Example 13.29
- Example 13.3
- Example 13.30
- Example 13.31
- Example 13.32
- Example 13.33
- Example 13.34
- Example 13.35
- Example 13.4
- Example 13.5
- Example 13.6
- Example 13.7
- Example 13.8
- Example 13.9
- Exercise16.1
- Exercise16.2
- Exercise16.3
- Exercise16.4
- Exercise16.5
- Exercise16.6
- Exercise16.7
- Exercise16.8
- Introductory Exercise
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Single Correct
- Match the columns
- Medical entranes gallery
- Miscellaneous Examples
- Solved Examples
- Subjective
- Subjective Question
- Taking it together