Complete Solutions to Level 1 Subjective of chapter CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
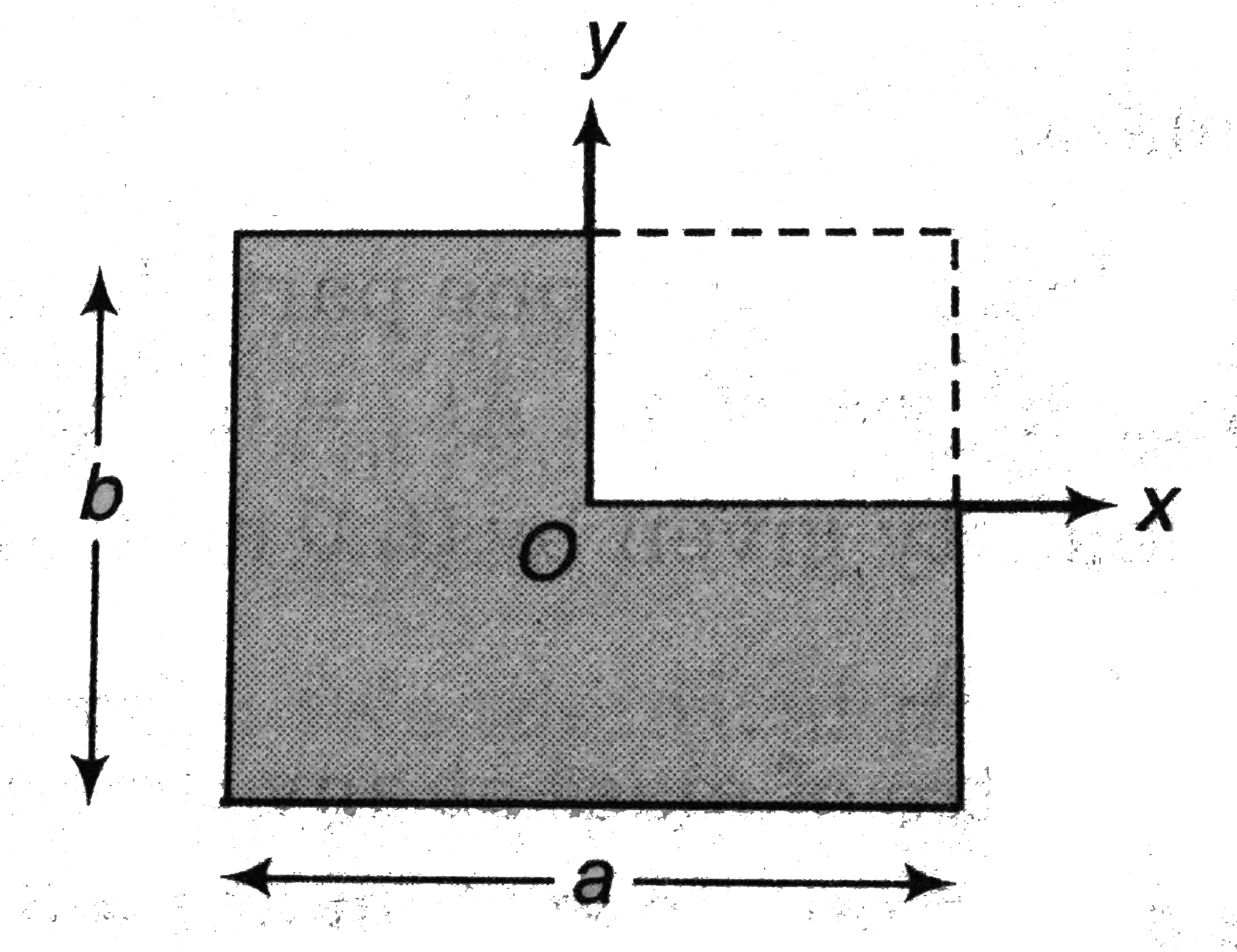
Consider a rectangular plate of dimensions `axxb`. If this plate is considered to be made up of four rectangles of dimensions `a/2xxb/2` and we now remove one out of four rectangles. Find the position where the centre of mass of the remaining system will lie?
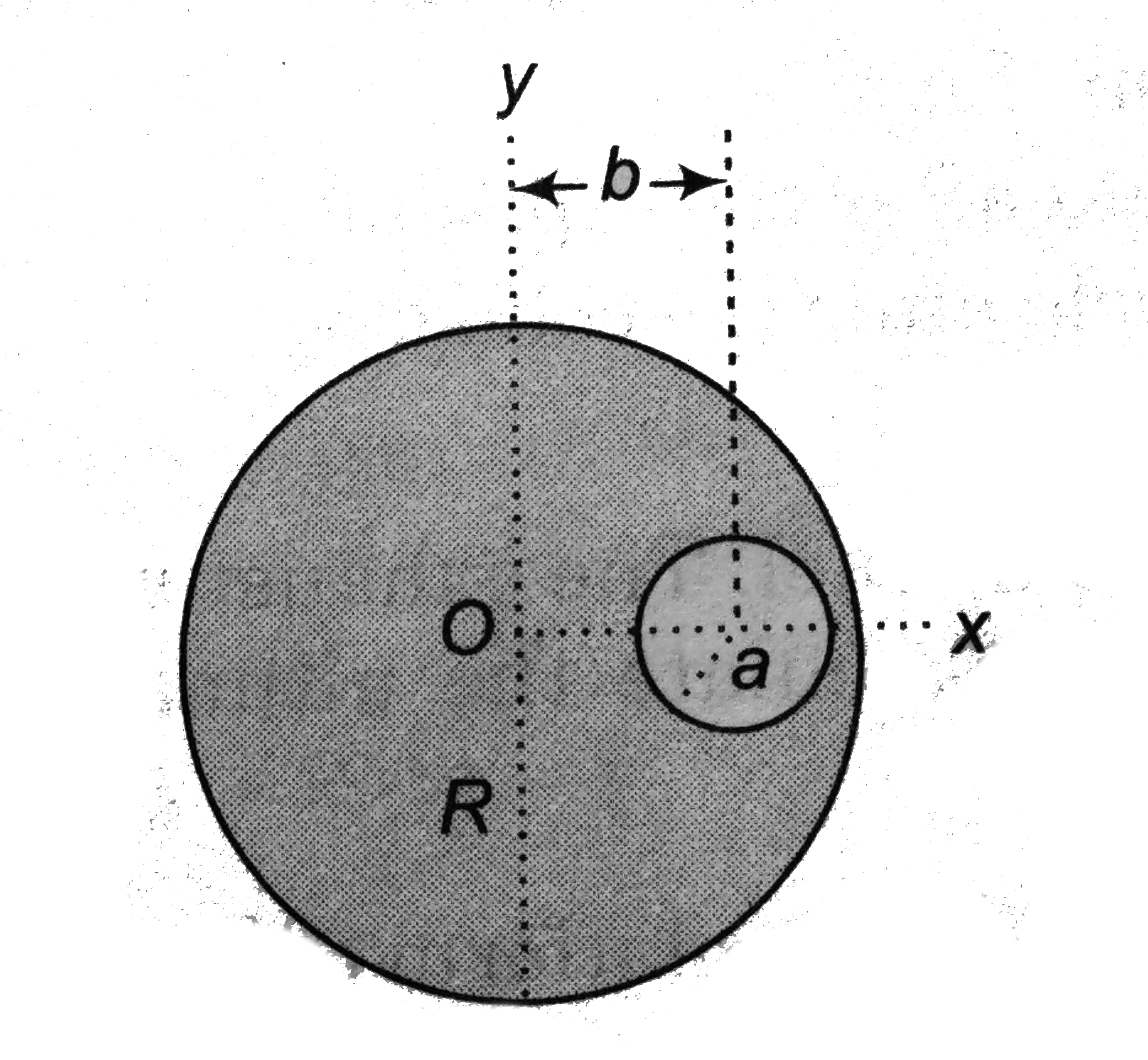
View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
View SolutionA gun fires a bullet. The barrel of the gun is inclined at an angle of `45^@` with horizontal. When the bullet leaves the barrel it will be travelling at an angle greater than `45^@` with the horizontal. Is this statement true or false?
View SolutionTwo blocks A and B of masses `m_A` and `m_B` are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionShow that in a head on elastic collision between two particles, the transference of energy is maximum when their mass ratio is unity.
View SolutionA particle moving with kinetic energy K makes a head on elastic collision with an identical particle at rest. Find the maximum elastic potential energy of the system during collision.
View SolutionA ball is projected from the ground at some angle with horizontal. Coefficient of restitution between the ball and the ground is e. Let a, b and c be the ratio of times of flight, horizontal range and maximum height in two successive paths. Find a, b and c in terms of e.

View Solution`x-y` is the vertical plane as shown in figure. A particle of mass `1kg` is at `(10m, 20m)` at time `t=0`. It is released from rest. Another particles of mass `2kg` is at `(20m, 40m)` at the same instant. It is projected with velocity `(10hati+10hatj)m//s`. After `1s`. Find (a) acceleration (b)velocity (c) position of the center of mass
View SolutionA system consists of two particles. At `t=0`, one particle is at the origin, the other, which has a mass of `0.60kg`, is on the y-axis at `y=80m`. At `t=0`, the centre of mass of the system is on the y-axis at `y=24m` and has a velocity given by `(6.0m//s)t^2hatj`.
(a) Find the total mass of the system.
(b) Find the acceleration of the centre of mass at any time t.
(c) Find the net external force acting on the system at `t=3.0s`.
View SolutionA particle of mass `2kg` moving with a velocity `5hatim//s` collides head-on with another particle of mass `3kg` moving with a velocity `-2hatim//s`. After the collision the first particle has speed of `1.6m//s` in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionA rocket of mass `40kg` has `160kg` fuel. The exhaust velocity of the fuel is `2.0km//s`. The rate of consumption of fuel is `4kg//s`. Calculate the ultimate vertical speed gained by the rocket. `(g=10m//s^2)`
View SolutionA boy of mass `60kg` is standing over a platform of mass `40kg` placed over a smooth horizontal surface. He throws a stone of mass `1kg` with velocity `v=10m//s` at an angle of `45^@` with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take `g=10m//s^2`.
View SolutionA man of mass `m` climbs to a rope ladder suspended below a balloon of mass `M`. The balloon is stationary with respect to the ground.
(a) If the man begins to climb the ladder at speed `v` (with respect to the ladder), in what direction and with what speed (with respect to the ground) will the balloon move?
(b) What is the state of the motion after the man stops climbing?
View SolutionFind the mass of the rocket as a function of time, if it moves with a constant acceleration `a`, in absence of external forces. The gas escapes with a constant velocity `u` relative to the rocket and its mass initially was `m_0`.
View SolutionA particle of mass `2m` is projected at an angle of `45^@` with horizontal with a velocity of `20sqrt2m//s`. After `1s` explosion takes place and the particle is broken into two equal pieces. As a result of explosion one part comes to rest. Find the maximum height attained by the other part. Take `g=10m//s^2`.
View SolutionA ball of mass `1kg` is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take `g=10m//s^2`)

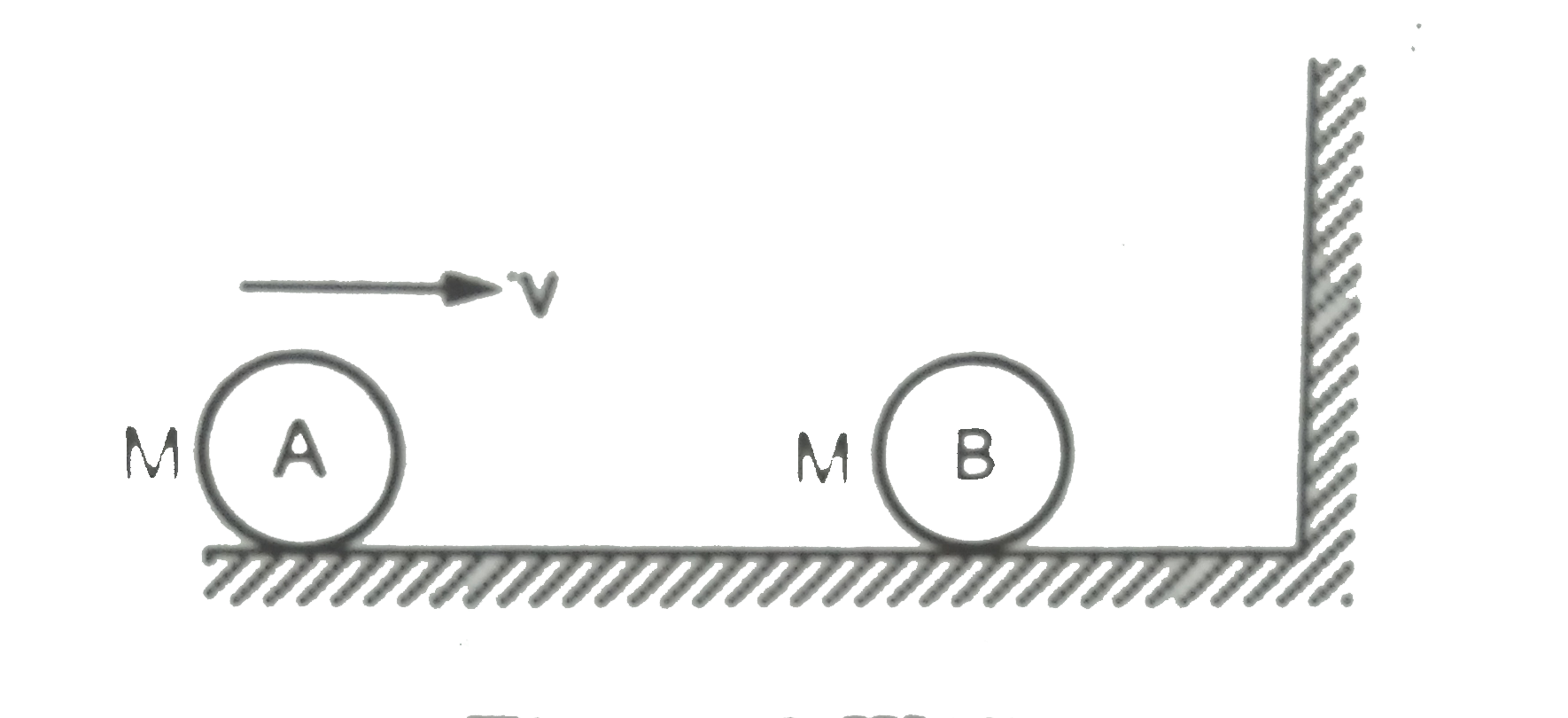
View SolutionThe two balls shwon in figure are indentical the first moving at a speed v towards right and the second staying at rest. The wall at the extreme right is fixed. Assume all collisions to be elastic. Show that the speeds of the balls remain unchanged after all the collisions have taken place.
View SolutionA particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
View SolutionA particle of mass `m` moving with a speed `v` hits elastically another staionary particle of mass `2m` on a smooth horizontal circular tube of radius `r`. Find the time when the next collision will take place?
View SolutionIn a one-dimensional collision between two identical particles. A and B, B is stationary and A has momentum `p` before impact. During impact, B gives an impulse J to A. Find the coefficient of restitution between A and B?
View SolutionTwo billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View SolutionTwo identical blocks each of mass `M=9kg` are placed on a rough horizontal surface of frictional coefficient `mu=0.1`. The two blocks are joined by a light spring and block B is in contact with a vertical fixed wall as shown in figure. A bullet of mass `m=1kg` and `v_0=10m//s` hits block A and gets embedded in it. Find the maximum compression of spring. (Spring constant `=240N//m, g=10m//s^2`)

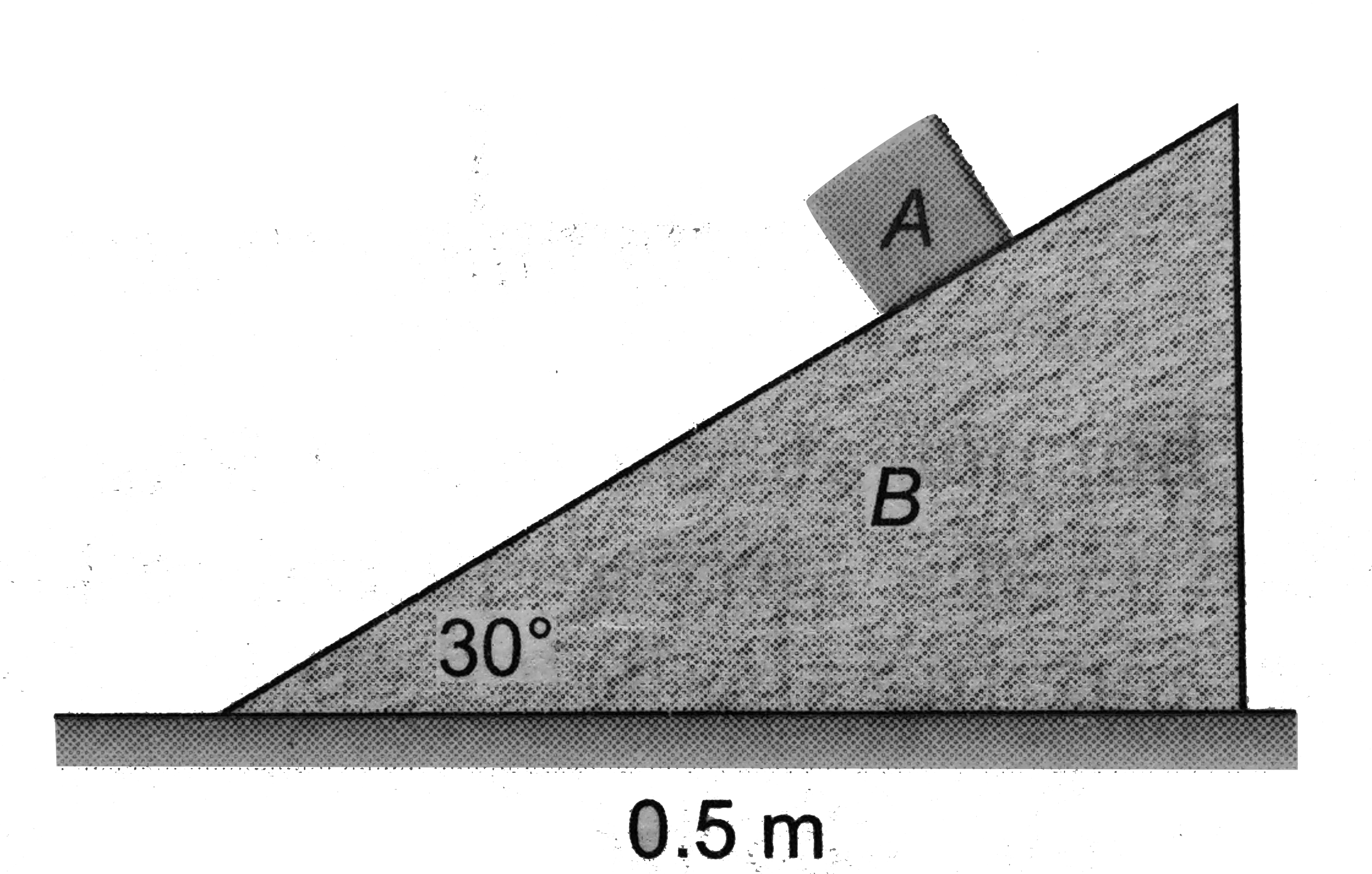
View SolutionBlock A has a mass of `5kg` and is placed on top of a smooth triangular block, B having a mass of `30kg`. If the system is released from rest, determine the distance, B moves when A reaches the bottom. Neglect the size of block A.
View SolutionA trolley was moving horizontally on a smooth ground with velocity `v` with respect to the earth. Suddenly a man starts running from rear end of the trolley with a velocity `(3//2)v` with respect to the trolley. After reaching the other end, the man turns back and continues running with a velocity `(3//2)v` with respect to trolley in opposite direction. If the length of the trolley is L, find the displacement of the man with respect to earth when he reaches the starting point on the trolley. Mass of the trolley is equal to the mass of the man.
View SolutionA `4.00g` bullet travelling horizontally with a velocity of magnitude `500m//s` is fired into a wooden block with a mass of `1.00kg`, initially at rest on a level surface. The bullet passes through the block and emerges with speed `100m//s`. The block slides a distance of `0.30m` along the surface from its initial position.
(a) What is the coefficient of kinetic friction between block and surface?
(b) What is the decrease in kinetic energy of the bullet?
(c) What is the kinetic energy of the block at the instant after the bullet has passed through it? Neglect friction during collision of bullet with the block.
View SolutionA wagon of mass `M` can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass `m` is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle `alpha` from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
View SolutionA block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

View SolutionA ball of mass 50 g moving at a speed of 2.0 m/s strikes a plane surface at an angle of incidence `45^0`. The ball is reflected by the plane at an equal angle of reflection with the same speed. Calculate (a). the magnitude of the change in momentum of the ball (b). the change in the magnitude of the mometum of the ball.
View SolutionA uniform rope of mass `m` per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length `y` of the rope has fallen, the force on the table is equivalent to the weight of the length `3y` of the rope.

View SolutionSand drops from a stationary hopper at the rate of `5kg//s` on to a conveyor belt moving with a constant speed of `2m//s`. What is the force required to keep the belt moving and what is the power delivered by the motor, moving the belt?
View SolutionA `3.0kg` block slides on a frictionless horizontal surface, first moving to the left at `50m//s`. It collides with a spring as it moves left, compresses the spring and is brought to rest momentarily. The body continues to be accelerated to the right by the force of compressed spring. Finally, the body moves to the right at `40m//s`. The block remains in contact with the spring for `0.020s`. What were the magnitude and direction of the impulse of the spring on the block? What was the spring's average force on the block?
View SolutionBlock A has a mass `3kg` and is sliding on a rough horizontal surface with a velocity `u_A=2m//s` when it makes a direct collision with block B, which has a mass of `2kg` and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is `mu_k=0.3` ( Take `g=10m//s^2`)
View Solution
Level 1 Subjective questions and complete solutions for chapter CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- Example
- Exercise 11.1
- Exercise 11.2
- Exercise 11.3
- Exercise 11.4
- Exercise 11.5
- Exercise 11.6
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 1 Subjective Questions
- Level 2 Comprehension Based
- Level 2 Comprehension Based Questions
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Single Correct Option
- Level 2 Subjective
- MiscellaneousExamples
- Solved Examples
- Type 1