Complete Solutions to Example of chapter CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION |
| DC PANDEY | Example |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
Two particles of masses 1kg and 2kg are located at `x=0` and `x=3m`. Find the position of their centre of mass.
View SolutionThe position vector of three particles of masses `m_1=1kg`.
`m_2=2kg` and `m_3=3kg` are `r_1=(hati+4hatj+hatk)m`, `r_2=(hati+hatj+hatk)m` and `r_3=(2hati-hatj-2hatk)m` respectively. Find the position vector of their centre of mass.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionA rod of length L is placed along the x-axis between `x=0` and `x=L`. The linear mass density (mass/length) `rho` of the rod varies with the distance x from the origin as `rho=a+bx`. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
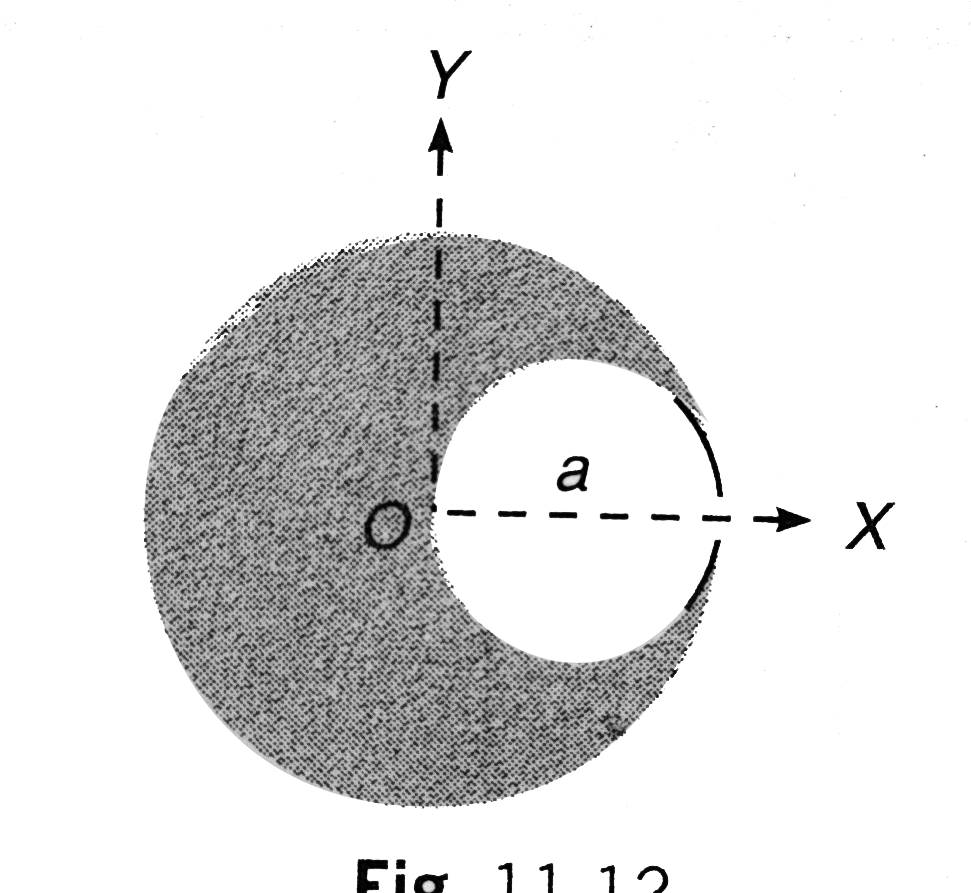
View SolutionTwo particles A and B of masses 1kg and 2kg respectively are projected in the directions shown in figure with speeds `u_A=200m//s` and `u_B=50m//s`. Initially they were `90m` apart. They collide in mid air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant.
`(g=10m//s^2)`

View SolutionIn the arrangement shown in Figure, `m_A=2kg` and `m_B=1kg`. String is light and inextensible. Find the acceleration of centre of mass of both the blocks. Neglect friction everywhere.

View SolutionTwo blocks A and B of equal masses are released on two sides of a fixed wedge C as shown in figure. Find the acceleration of centre of mass of blocks A and B. Neglect friction.
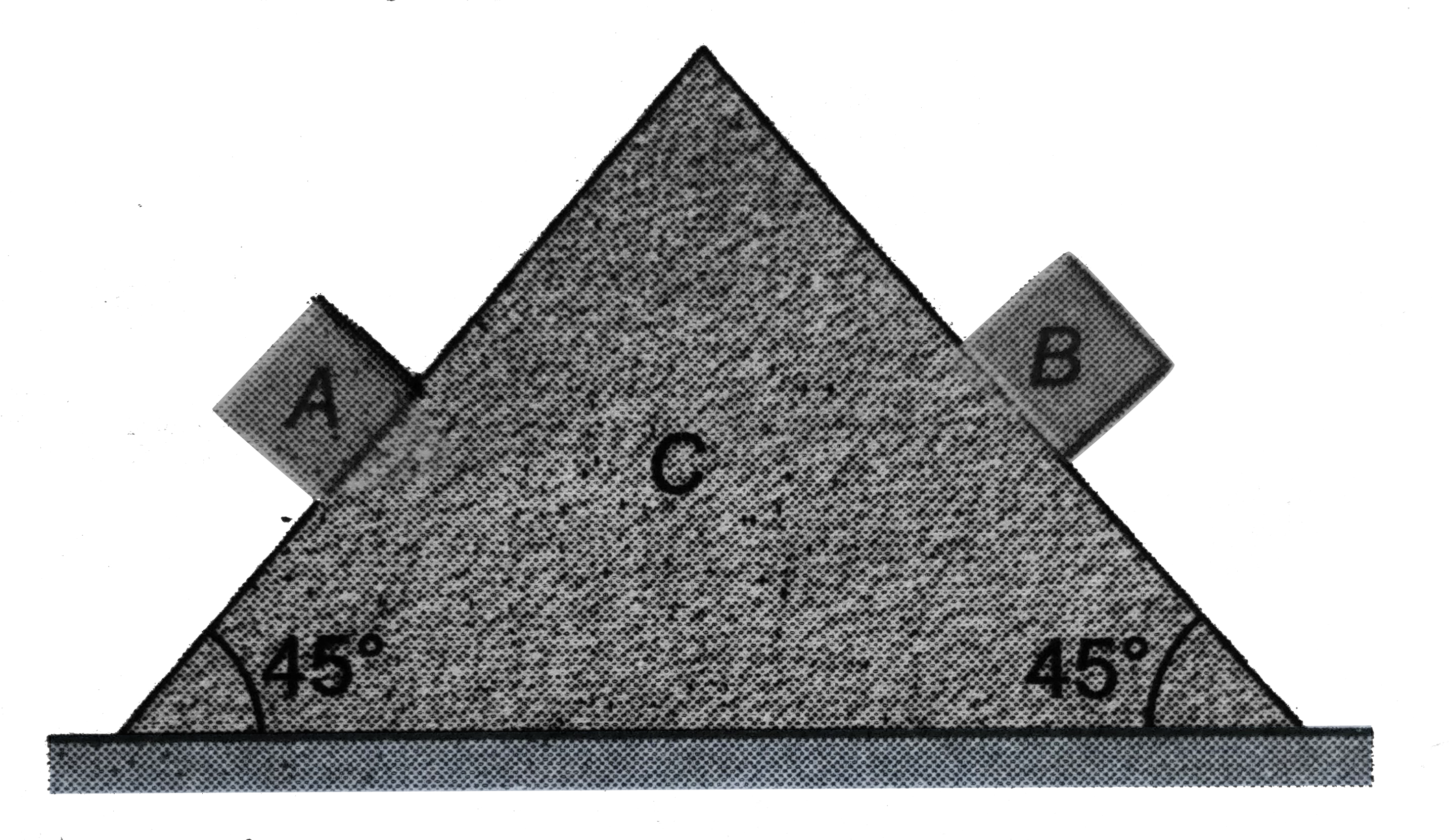
View SolutionLinear momentum of particle is increased by
(a) 100% (b) 1%
without changing its mass. Find percentage increase in its kinetic energy in both cases.
View SolutionKinetic energy of a particle is increased by
(a) 50% (b) 1%
Find percentage change in linear momentum.
View SolutionTwo blocks A and B of masses 1kg and 2kg are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Find the ratio of their,
(a) speed
(b) magnitude of momentum and
(c) kinetic energy at any instant.
View SolutionA gum (mass=M) fires a bullet (mass=m) with speed `v_r` relative to barrel of the gum which is inclined at an anlge of `60^@` with horizontal. The gun is placed over a smooth horizontal surface. Find the recoil speed of gun.
View SolutionA projectile of mass 3m is projected from ground with velocity `20sqrt2 m//s` at `45^@`. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of `100m` from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
`(g=10m//s^2)`
View Solution(a) A rocket set for vertical firing weighs `50kg` and contains `450kg` of fuel. It can have a maximum exhaust velocity of `2km//s`. What should be its minimum rate of fuel consumption
(i) to just lift off the launching pad?
(ii) to give it an initial acceleration of `20m//s^2`?
(b) What will be the speed of the rocket when the rate of consumption of fuel is `10kg//s` after whole of the fuel is consumed? (Take `g=9.8m//s^2`)
View SolutionA ball of mass 200g is projected with a density of `30m//s` at `30^@` from horizontal. Using the concept of impulse, find change in velocity in 2s. Take `g=10m//s^2`.
View SolutionA time varying force, `F=2t` is acting on a particle of mass `2kg` moving along x-axis. velocity of the particle is `4m//s` along negative x-axis at time `t=0`. Find the velocity of the particle at the end of 4s.
View SolutionA particle of mass `2kg` is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of `10s`.

View SolutionA bullet of mass `10^-3kg` strikes an obstacle and moves at `60^@` to its original direction. If its speed also changes from `20m//s` to `10m//s`. Find the magnitude of impulse acting on the bullet.
View SolutionTwo blocks A and B of equal mass `m=1.0kg` are lying on a smooth horizontal surface as shown in figure. A spring of force constant `k=200N//m` is fixed at one end of block A. Block B collides with block A with velocity `v_0=2.0m//s`. Find the maximum compression of the spring.

View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and `2v`. Find their velocities after collision.
View SolutionTwo pendulum bobs of masses m and `2m` collide head on elastically at the lowest point in their motion. If both the balls are released from a height H above the lowest point, to what heights do they rise for the first time after collision?
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is `3/4th` of the original. Find the coefficient of restitution.


View SolutionA ball is moving with velocity `2m//s` towards a heavy wall moving towards the ball with speed `1m//s` as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball of mass m hits a floor with a speed `v_0` making an angle of incidence `alpha` with the normal. The coefficient of restitution is `e`. Find the speed of the reflected ball and the angle of reflection of the ball.
View SolutionAfter a completely inelastic collision two objects of the same mass and same initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.
View SolutionThe coefficient of restitution between a snooker ball and the side cushion is `1/3`. If the ball hits the cushion and then rebounds at right angles to its original direction, show that the angles made with the side cushion by the direction of motion before and after impact are `60^@` and `30^@` respectively.
View Solution
Example questions and complete solutions for chapter CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- Example
- Exercise 11.1
- Exercise 11.2
- Exercise 11.3
- Exercise 11.4
- Exercise 11.5
- Exercise 11.6
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 1 Subjective Questions
- Level 2 Comprehension Based
- Level 2 Comprehension Based Questions
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Single Correct Option
- Level 2 Subjective
- MiscellaneousExamples
- Solved Examples
- Type 1