Complete Solutions to Exercise 14.2 of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY | Exercise 14.2 |
| Number Of Questions | 5 |
| Academic Year | 2023-24 |
Given that the equation of motion of a mass is `x = 0.20 sin (3,0 t) m` . Find the velocity and acceleration of the mass when the object is `5 cm` from its equilibrium position. Repeat for `x = 0`.
View SolutionA particle executes simple harmonic motion of amplitude `A` along the x - axis. At `t = 0`, the position of the particle is `x = (A)/(2)` and it moves along the positive x - direction. Find the phase contant `delta`, if of the equation is written as `x = Asin (omega t + delta)`.
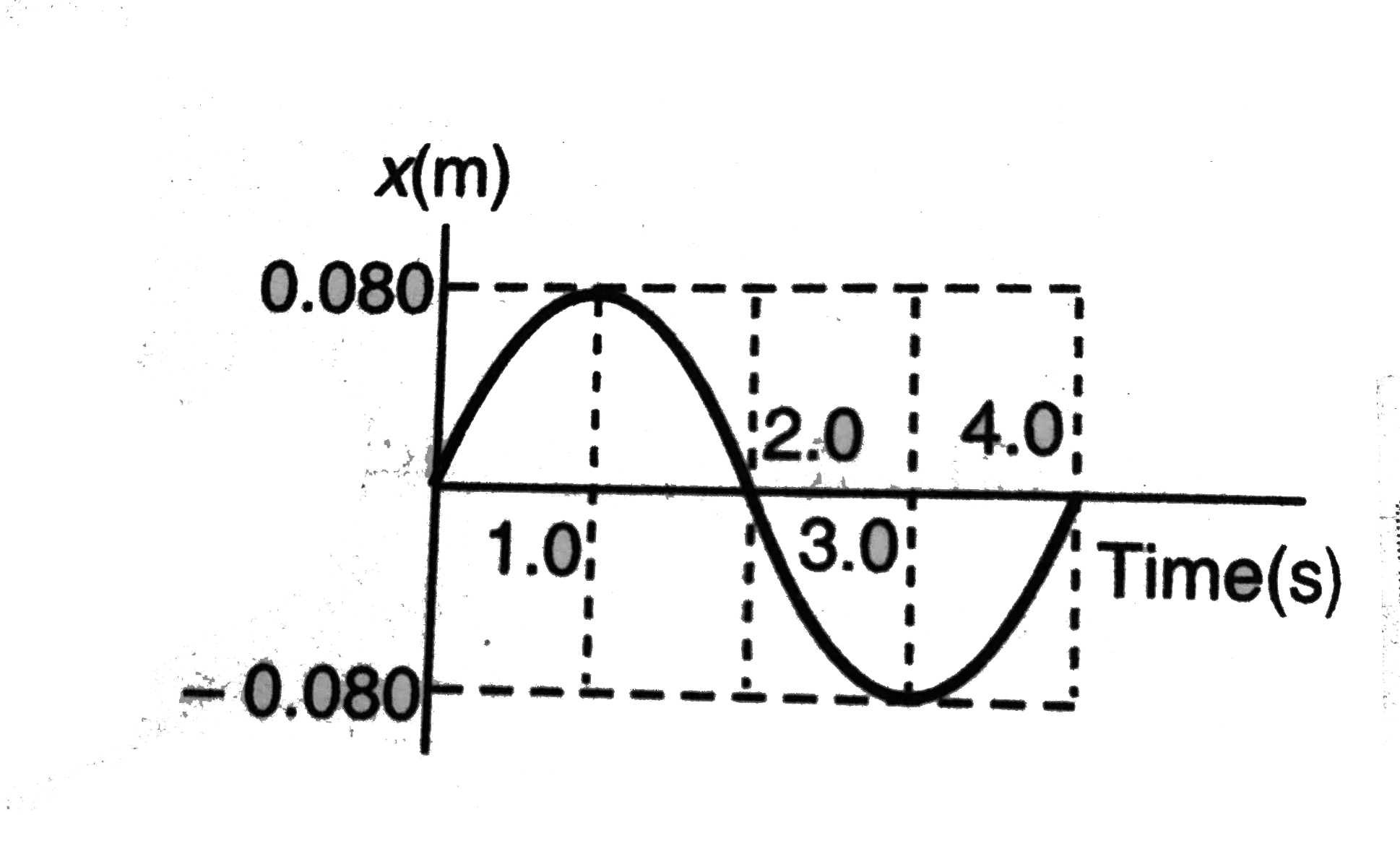
View SolutionAn object of mass `0.8kg` is attached to one end of a spring and the system is set into simple harmonic motion. The displacement `x` of the object as a fuction of time is shown in the figure. With the aid of the data, determine
(a) the amplitude `A` of the motion,
(b) the angular frequency `omega`,
( c) the spring constant `K`,
(d) the speed of the object at `t = 1.0 s` and
(e) the magnitude of the object's acceleration at `t = 1.0 s`.
View SolutionThe equation of motion of a particle started at t=0 is given by `x=5sn(20t+pi/3)`, where x is in centimetre and t in second. When does the particle
a. first come rest
b. first have zero acceleration
c. first have maximum speed?
View SolutionDescribe the motion corresponding to `x - t` equation, `x = 10 - 4cos omega t`.
View Solution
Exercise 14.2 questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct