Complete Solutions to Level 2 Subjective of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY | Level 2 Subjective |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
A `1kg` block is executing simple harmonic motion of amplitude `0.1m` on a smooth horizontal surface under the restoring force of a spring of spring constant `100 N//m`. A block of mass `3 kg` is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together. Find the frequency and the amplitude of the motion.
View SolutionTwo particles are in SHM along same line. Time period of each is `T` and amplitude is `A`. After how much time will they collide if at time `t = 0`. (a) first particle is at `x_(1) = + (A)/(2)` and moving towards positive x - axis and second particle is at `x_(2) = - (A)/(sqrt2)` and moving towards negative x - axis, (b) rest information are same as mentioned in part (a) except that particle first is also moving towards negative x - axis.
View SolutionA particle that hangs from a spring oscillates with an angular frequency of `2 rad//s`. The spring particle system is suspended from the celling of an elevator car and hangs motionless (relative to the elevator car) as the car descends at a constant speed of `1.5 m//s`. The car then stops suddenly. (a) With what amplitude does the particle oscillate ? (b) What is the equation of motion for the particle ? (Choose upward as the position diriction)
View SolutionA `2kg ` mass is attached to a spring of force constant `600 N//m` and rests on a smooth horizontal surface. A second mass of `1kg` slides along the surface toward the first at `6m//s`.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position `x` as a function of time `t` for the mass attached to the spring, assuming that the collision occurs at time `t = 0`. What is the impulse given to the `2kg mass in each case ?
View SolutionA block of mass `4kg` hangs from a spring of force constant `k = 400 N//m`. The block is pulled down `15 cm` below equilibrium and relesed. How long does it take block to go from `12 cm` below equilibrium (on the way up) to `9cm` above equilibrium ?
View SolutionA plank with a body of mass `m` placed on it starts moving straight up according to the law `y = a(1 - cos omega t)`, where `y` is the displacement from the initial position, `omega = 11 rad//s`. Find
(a) The time independence of the force that the body exerts on the plank.
(b) The minimum amplitude of oscillations of the plank at which the body starts falling behind the plank.
View SolutionA particle of mass `m` free to move in the `x - y` plane is subjected to a force whose components are `F_(x) = - kx` and `F_(y) = - ky`, where `k` is a constant. The particle is released when `t = 0` at the point `(2, 3)`. Prove that the subsequent motion is simple harmonic along the straight line `2y - 3x = 0`.
View SolutionDetermine the natural frequency of vibration of the `100N` disk. Assume the disk does not slip on the inclined surface.

View SolutionThe disk has a weight of `100 N`and rolls without slipping on the horizontal surface as it oscillates about its equilibrium position. If the disk is displaced, by rolling it counterclockwise `0.4rad`, determine the equation which describes its oscillatory motion when it is released.
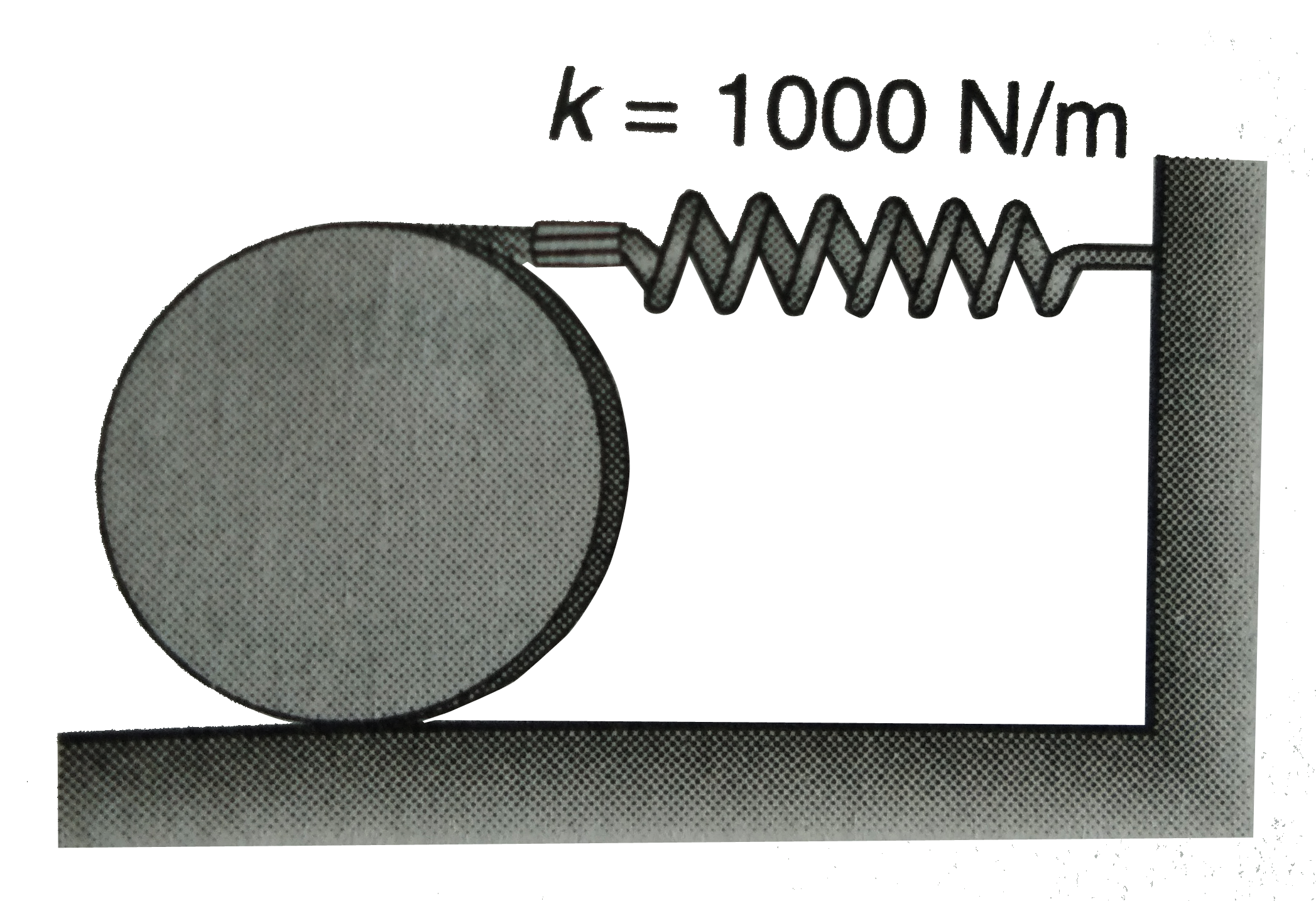
View SolutionA solid uniform cylinder of mass `m` performs small oscillations due to the action of two springs of stiffness `k` each (figure). Find the period of these oscillation in the absendce of sliding.
`x`
View SolutionA block of mass `m` is attached to one end of a light inextensible string passing over a smooth light pulley `B` and under another smooth light pulley `A` as shown in the figure. The other end of the string is fixed to a ceiling. `A` and `B` are held by spring of spring constants `k_(1)` and `k_(2)`. Find angular frequency of small oscillations of small oscillations of the system.

View SolutionIn the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between `m_(2)` and `m_(1)` is `mu`. There is no friction between `m_(1)` and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock `m_(2)` is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?
View SolutionTwo block `A` and `B` of masses `m_(1) = 3kg` and `m_(2) = 6kg` respectively are connected with each other by a spring of force constant `k = 200 N//m` as shown in figure. Blocks are pulled away from each other by `x_(0) = 3cm` and then released. When spring is in its natural length and block are moving towards each other, another block `C` of mass `m = 3kg` moving with velocity `v_(0) = 0.4m//s` (towards right) collides with `A` and gets stuck to it. Neglecting friction, calculate
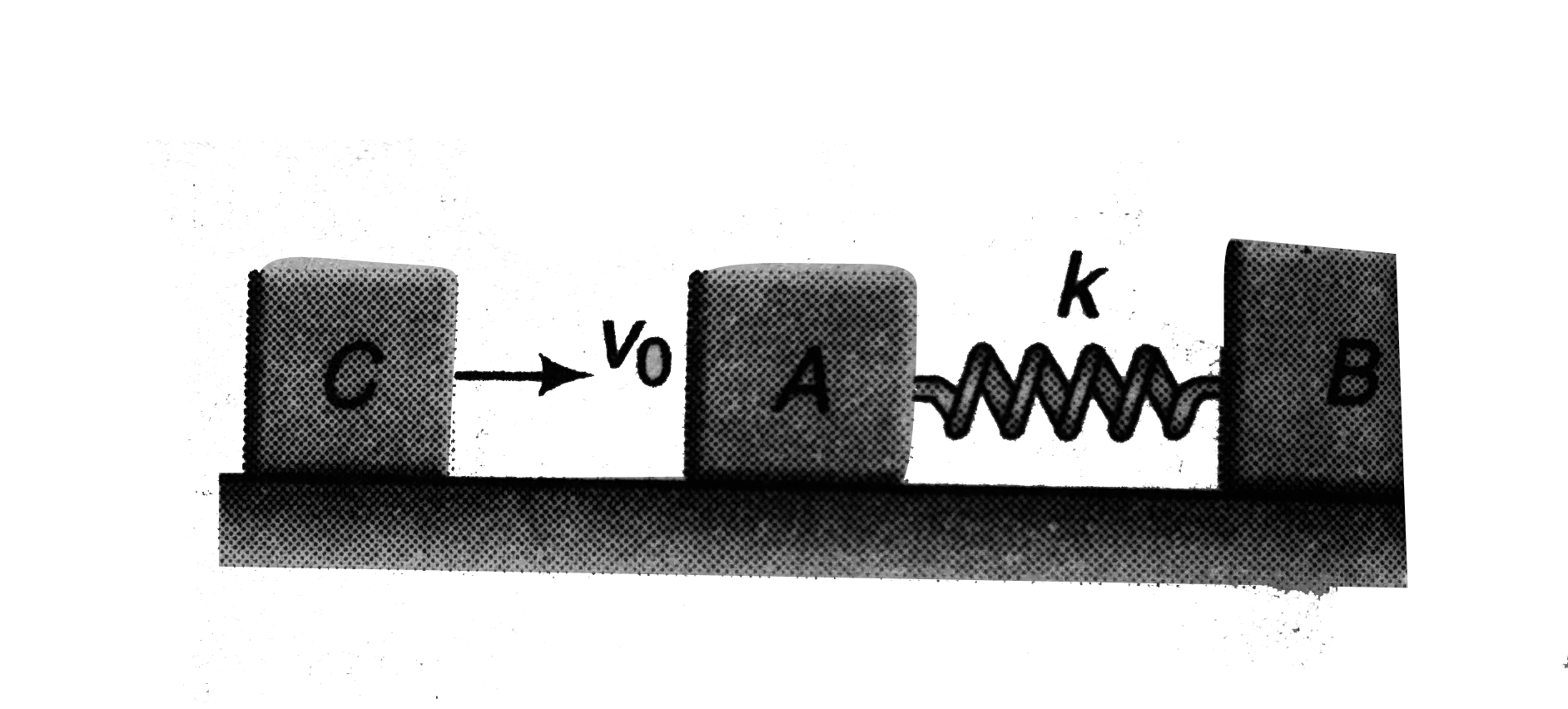
(a) velocity `v_(1)` and `v_(2)` of the blocks `A` and `B` respectively just before collision and their angular frequency .
(b) velocity of centre of mass of the system, after collision,
( c) amplitude of oscillation of combined body,
(d) loss of energy during collision.
View SolutionA rod of length `l` and mass `m`, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant `k`. Find the frequency of small oscillations about the equilibrium position.
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. `K_(1)`, `k_(2)`, `k_(3)`and `k_(4)` are force constant of the spring. Calculate period of small vertical oscillations of block of mass `m`.

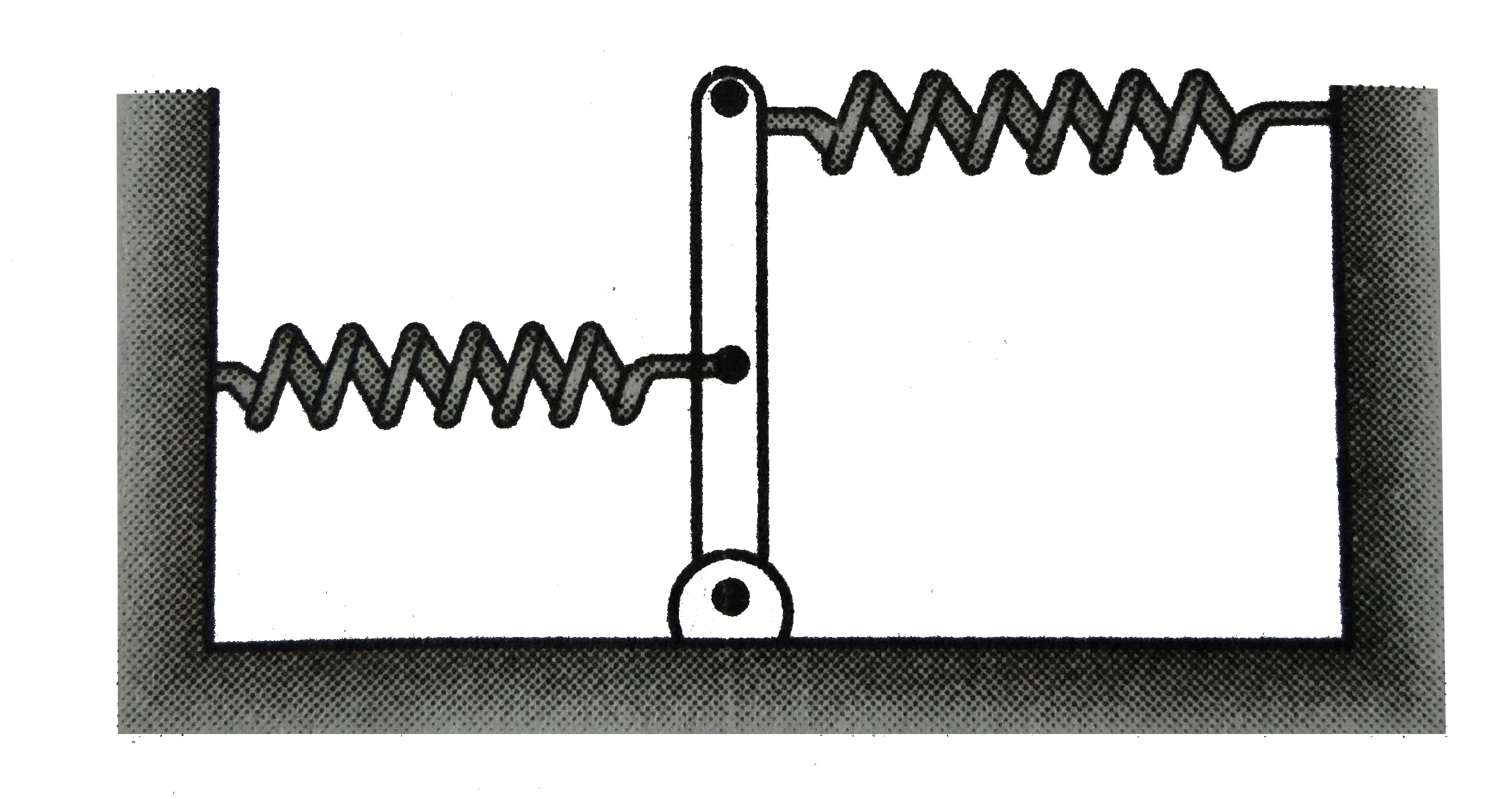
View SolutionA light pulley is suspended at the lower end of a spring of constant `k_(1)`, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass `m` is suspended, the other end of the string is attached to another spring of constant `k_(2)`. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass `m` about equilibrium position.

View SolutionFigure shows a solid uniform cylinder of radius `R` and mass `M`, which is free to rotate about a fixed horizontal axis `O` and passes through centre of the cylinder. One end of an ideal spring of force constant `k` is fixed and the other end is higed to the cylinder at `A`. Distance `OA` is equal to `(R)/(2)`. An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass `M` and having cross sectional area `A` is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density `rho`.
If in equilibrium, spring is horizontal and line `OA` is vertical, calculate frequency of small oscillations of the system.
`
View SolutionFind the natural frequency of the system shown in figure. The pulleys are smooth and massless.

View Solution
Level 2 Subjective questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct