Complete Solutions to JEE Advanced of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | JEE Advanced |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
A particle moves such that its acceleration is given by `a = -Beta(x-2)`
Here, `Beta` is a positive constnt and x the x-coordinate with respect to the origin. Time period of oscillation is
View SolutionA particle starts oscillating simple harmoniclaly from its equilibrium postion. Then the ratio fo kinetic and potential energy of the principle at time `T/12` is (`U_(mean)`=0, T= Time period)
View SolutionA mass `m = 8kg` is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is `200 N//m`. The mass `m` is then released and begins to undergo small oscillations. The maximum velocity of the mass will be `(g=10m//s^(2))`
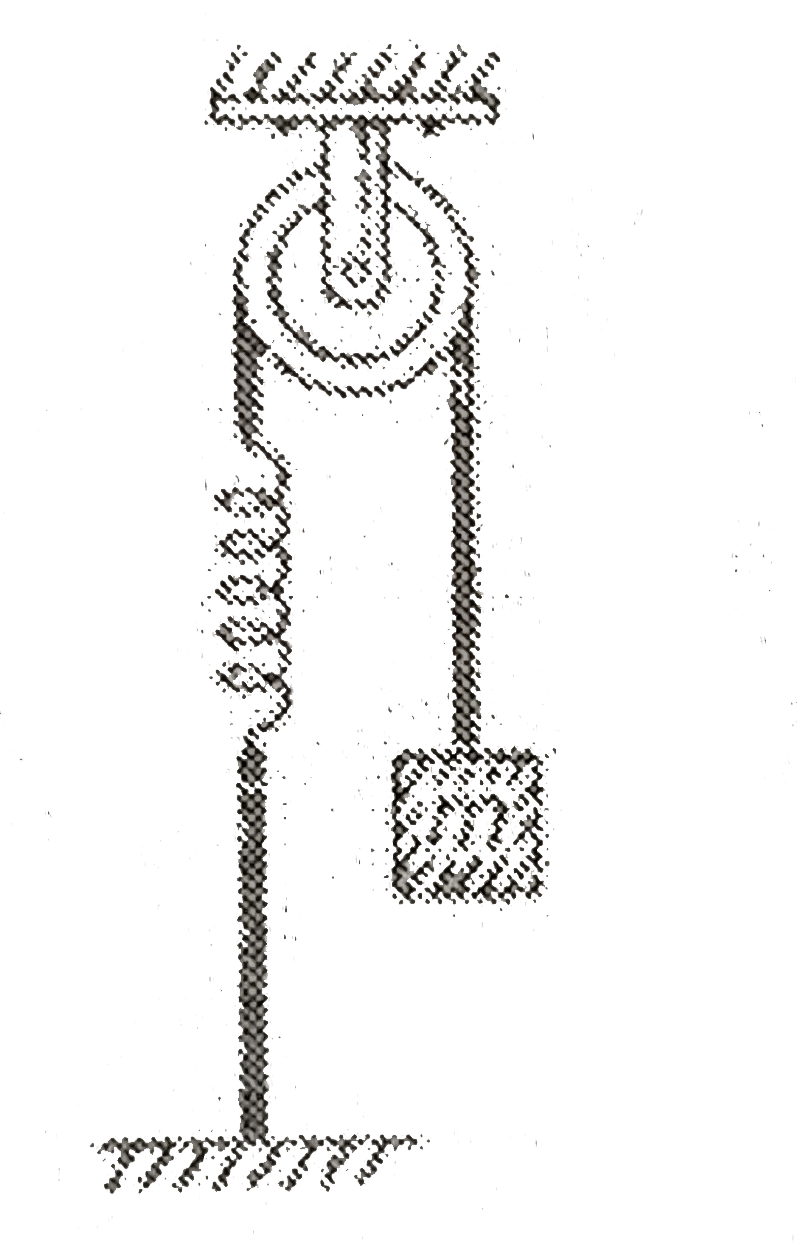
View SolutionAn block rides on position that is moving vertically with simple harmonic motion. The maximum speed of the piston is 2m/s. At what minimum amplitude of motion will the block and piston separate? (g=10m/`s^(2)`)
View SolutionAn accurate pendulum clock is mounted on ground floor of a high building. How much time will it lose or gain in one day if its is transferred to top storey of a building which is h = 200m higher than the ground floor? Radius of earth is `6.4 xx 10^(6)`
View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View SolutionVertical displacement of a plank with a body of mass m on it is varying according to the law `y=sinomegat+sqrt(3)cosomegat`. The minimum value of `omega` for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).
View SolutionThe displacement-time equation of a particle executing SHM is `A-Asin(omegat+phi)`. At tme t=0 position of the particle is x=`A/2` and it is moving along negative x-direction. Then the angle `phi` can be
View SolutionThe maximum tension in the string of a pendulum is two times the minimum tension. Let `theta_(0)` is
View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are kept on a smooth horizontal table as shown in figure. Block of mass `m_(1)` (but not `m_(2)` is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass `m_(1)` after the system is released is
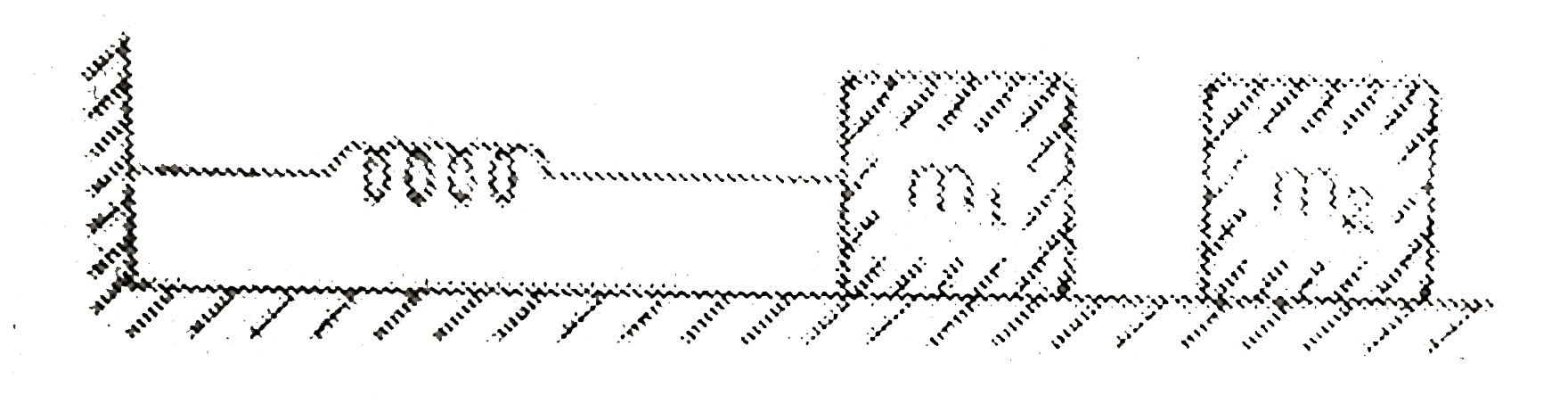
View SolutionTime period of a simple pendulum of length L is `T_(1)` and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is `T_(2)`. Amplitude of osciallations in both the cases is small. Then `T_(1)/T_(2)` is
View SolutionThe potential energy of a particle of mass 1 kg in motin along the x-axis is given by
U = 4(1-cos2x)J
Here, x is in meter. The period of small osciallationis (in second) is
View SolutionA particle executing SHM while moving from one extremity is found at distance `x_(1),x_(2)` and `x_(3)` from the center at the end of three successive seconds. The time period of oscillatin is
Here `theta=cos^(-1)((x_(1)+x_(3))/(2x_(2))`
View SolutionTwo particles are executing SHM in a straight line. Amplitude A and the time period T of both the particles are equal. At time t=0, one particle is at displacement `x_(1)=+A` and the other `x_(2)=(-A/2)` and they are approaching towards each other. After what time they across each other? `T/4`
View SolutionMaximum speed of a particle in simple harmonic motion is `v_(max)`. Then average speed of this particle in one time period is equal to
View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is `1/2`. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/`s^(2)`)
View SolutionA particle of mass m is executing osciallations about the origin on the x-axis with amplitude A. its potential energy is given as `U(x)=alphax^(4)`, where `alpha` is a positive constant. The x-coordinate of mass where potential energy is one-third the kinetic energy of particle is
View SolutionA ball of mass m when dropped from certain height as shown in diagram, strikes a wedge kept on smooth horizontal surface and move horizontally just after impact. If the ball strikes the ground at a distance d from its initial line of fall, thenthe amplitude of oscillation of wedge after being hit by the ball will be
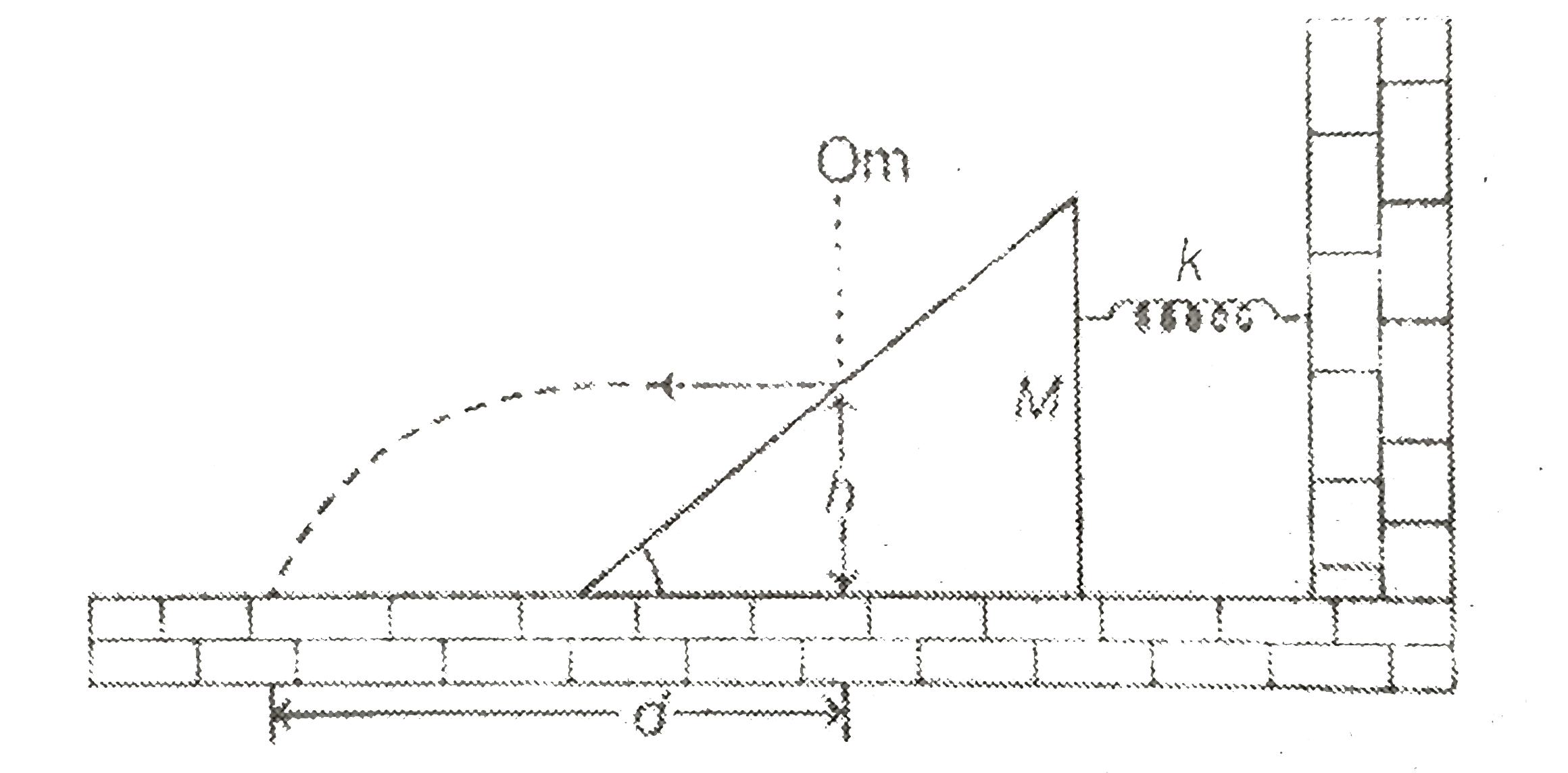
View SolutionA particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the SHM is
View SolutionThe angular frequency of a spring block system is `omega_(0)`. This system is suspended from the ceiling of an elevator moving downwards with a constant speed `v_(0)`. The block is at rest relative to the elevator. Lift is suddenly stopped. Assuming the downward as a positive direction. Then
View SolutionA small ball of density `rho` id released from rest from the surface of a liquid whose density varies with depth `h` as `rho=(rho_(0))/2(alpha+betah)`. Mass of the ball is `m`. Select the most appropriate option.
View SolutionA constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is

View SolutionTwo blocks of masses `m_(1)`=1kg and `m_(2)` = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block `m_(1)` is imparted an initial velocity `v_(0)` = 12cm/s to the right. The amplitude of osciallation is
View SolutionU.r graph of a particle performing SHM is as shown in figure. What conclusion cannot be drawn from the graph?
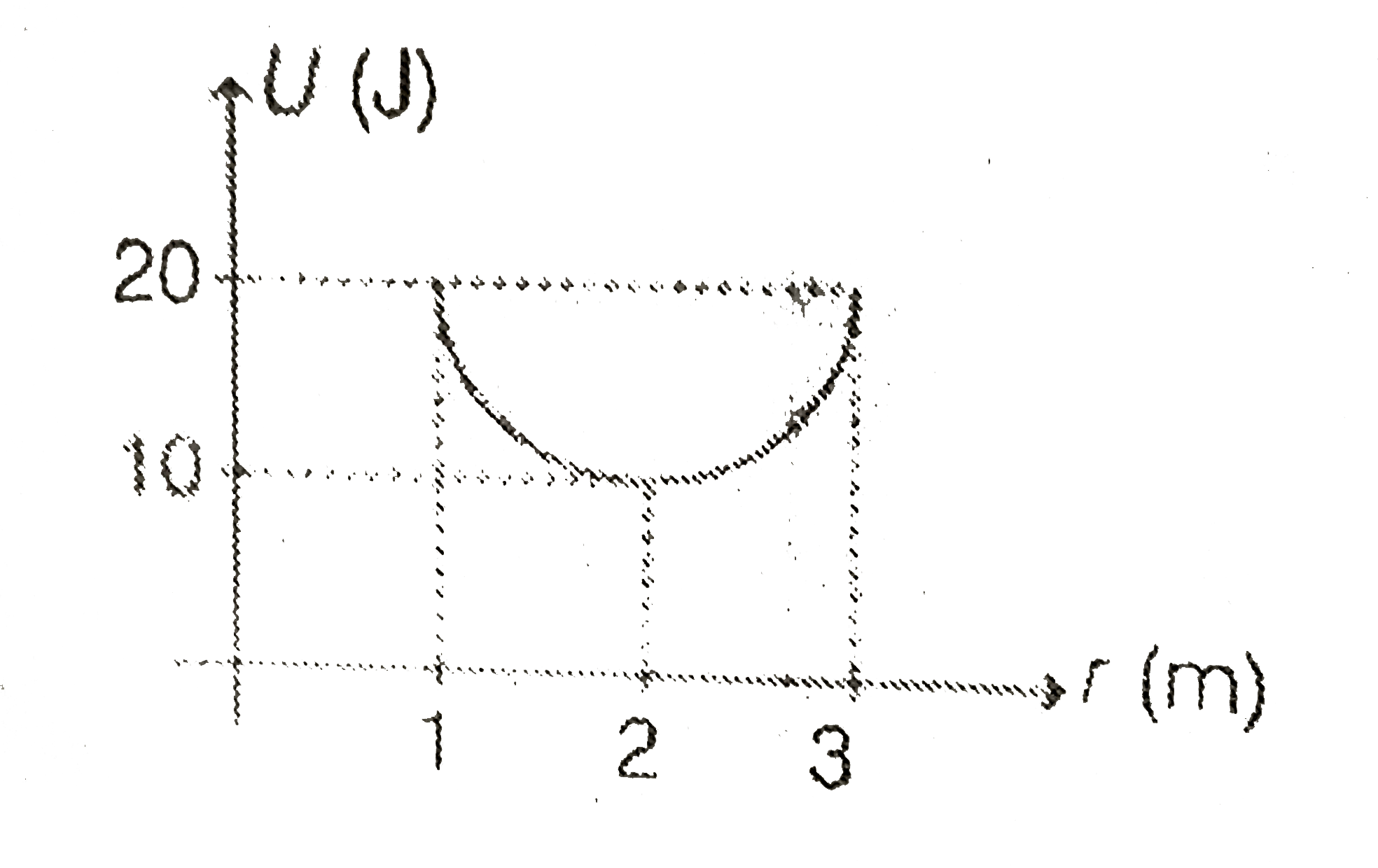
View SolutionTwo particles are in SHM along same line with same amplitude A and same time period T. At time t=0, particle 1 is at + `A/2` and moving towards positive x-axis. At the same time particle 2 is at `-A/2` and moving towards negative x-axis. Find the timewhen they will collide.
View SolutionA plank of area of cross-section A is half immersed in liquid 1 of density `rho` and half in liquid 2 of density `2rho`. What is period of osciallation of the plank if it is slightly depressed downwards?

View SolutionA mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionA test tube of length l and area of cross-section A has some iron fillings of mass M. The test tube floats normally in a liquid of density `rho` with length x dipped in the liquid. A distribuing force makes the tube oscillate in the liquid. The time period of osciallation is given by (neglect the mass of the test tube)
View SolutionA particle is executing SHM according to the equation x`=A cosomegat`. Average speed of the particle during the interval `0larrtlarrpi/(6omega)`
View SolutionA particle performs `SHM` of amplitude `A` along a straight line .When it is at a distance of `sqrt(3)/(2)`A from mean position its kinetic energy gets increased by an amount of `(1)/(2) m omega^(2)A^(2)` due to an impulsive force. Then its new amplitude becomes
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
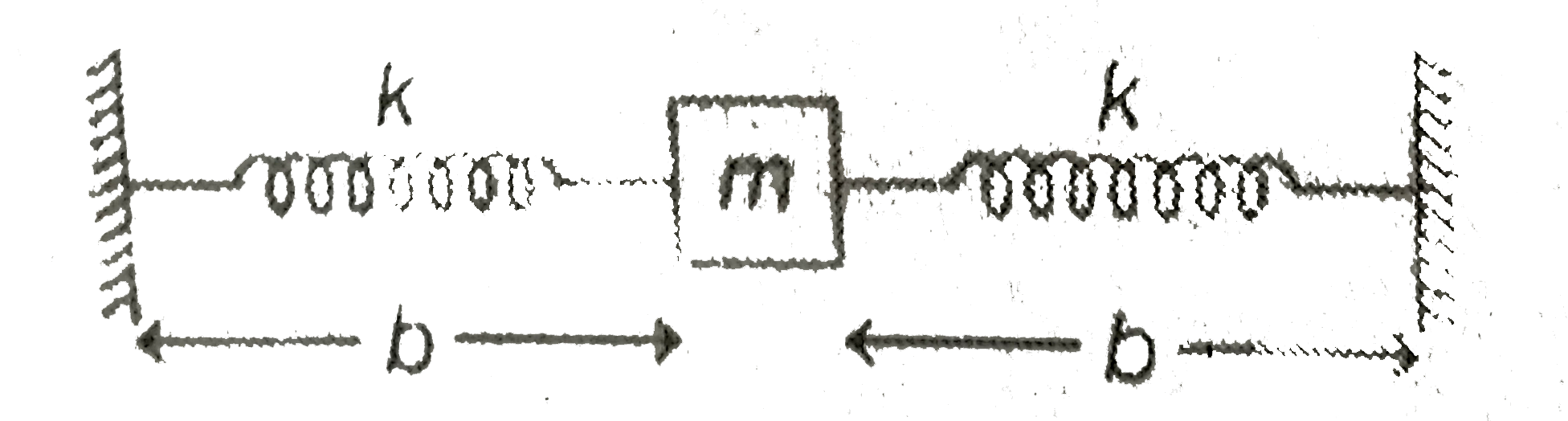
View SolutionA particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin `x^(2)`=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/`s^(2))`
View SolutionTwo springs, each of spring constant k = 100N/m are attached to a block of mass 2kg as shown in figure. The block can slide smoothly along horizontal platform clamped to the opposite walls of a trolley of mass 5kg. The block is slightly displace dand then released. The period of oscillation is (in seconds). (all surfaces are smooth)

View Solution
JEE Advanced questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct