Complete Solutions to Only one question is correct of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY MASTER PROBLEM PACKAGE | Only one question is correct |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
A student says that he had applied a force `F=-ksqrt(x)` on a particle and the particle performs in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle.
View SolutionEquation of SHM is x=10sin10`pit`. Find the distance between the two points where speed is `50pi`cm/s. x is in cm and t is in seconds.
View SolutionAcceleration versus time graph of a body in SHM is given by a curve shown below. T is the time period. Then corresponding graph between kinetic energy KE and time t is correctly represented by

View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is

View SolutionA scientist measures the time period of a simple pendulum as T in a lift at rest. If the lift moves up with accelerationi as one fourth of the acceleratioin of gravity, the new time period is

View SolutionThe osciallations represented by curve 1 in the graph are expressed by equation `x=A sinepsilont`. The equation for the oscillations represented by curve 2 is expressed as

View SolutionA cuboidal piece of wood has dimensions `a, b` and `c`. its relatively density is `d`. it is floating in a large body of water such that side `a` is vertical. It is pushed down a bit and released. The time period of SHM executed by it is
View SolutionThe time taken by a particle performing SHM to pass from point A and B where it is velocities are same is `2:3`. After another 2 s it returns to B. The time period oscillation is (in seconds)
View SolutionTwo particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At particular instant, one particle is at its extreme position while the other is at its mean position. The move in the same direction. They will cross each other after a further time.
View SolutionA particle performing SHM is found at its equilibrium position at t = 1s and it is found to have a speed 0.25 = m//s at t=2s. If the period of oscillation is 6. Calculate amplitude of oscillation.
View SolutionA particle is subjected to two mutually perpendicualr simple harmonic motions such that its x and y-coordinates are given by
`x=sinomegat`, `y=2cosomegat`
The path of the particle will be :
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
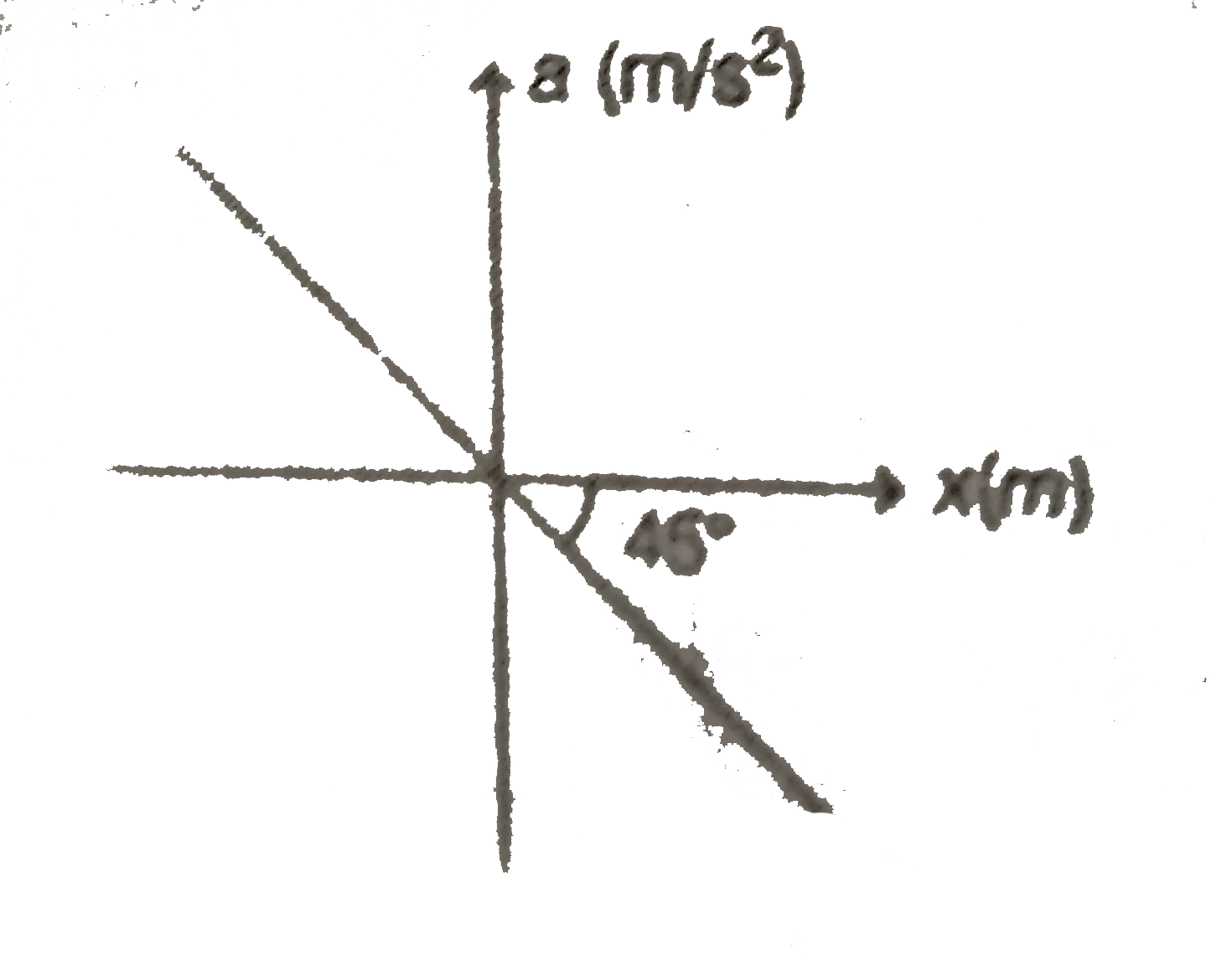
View SolutionA particle of mass 0.1 kg executes SHM under a for `F=(-10x)` N. Speed of particle at mean position `6m//s`. Then amplitude of oscillations is
View SolutionDisplacement-time equation of a particle execution SHM is x=A sin(`omegat+pi/6)`
Time taken by the particle to go directly from
`x = -A/2 to x = + A/2 is `
View SolutionDisplacement-time graph of a particle executing SHM is as shown

The corresponding force-time graph of the particle can be
View SolutionA uniform disc of radius R is pivoted at point O on its circumstances. The time period of small oscillations about an axis passing through O and perpendicular to plane of disc will be
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is `pi/2`. The resultant path followed by the particle is
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
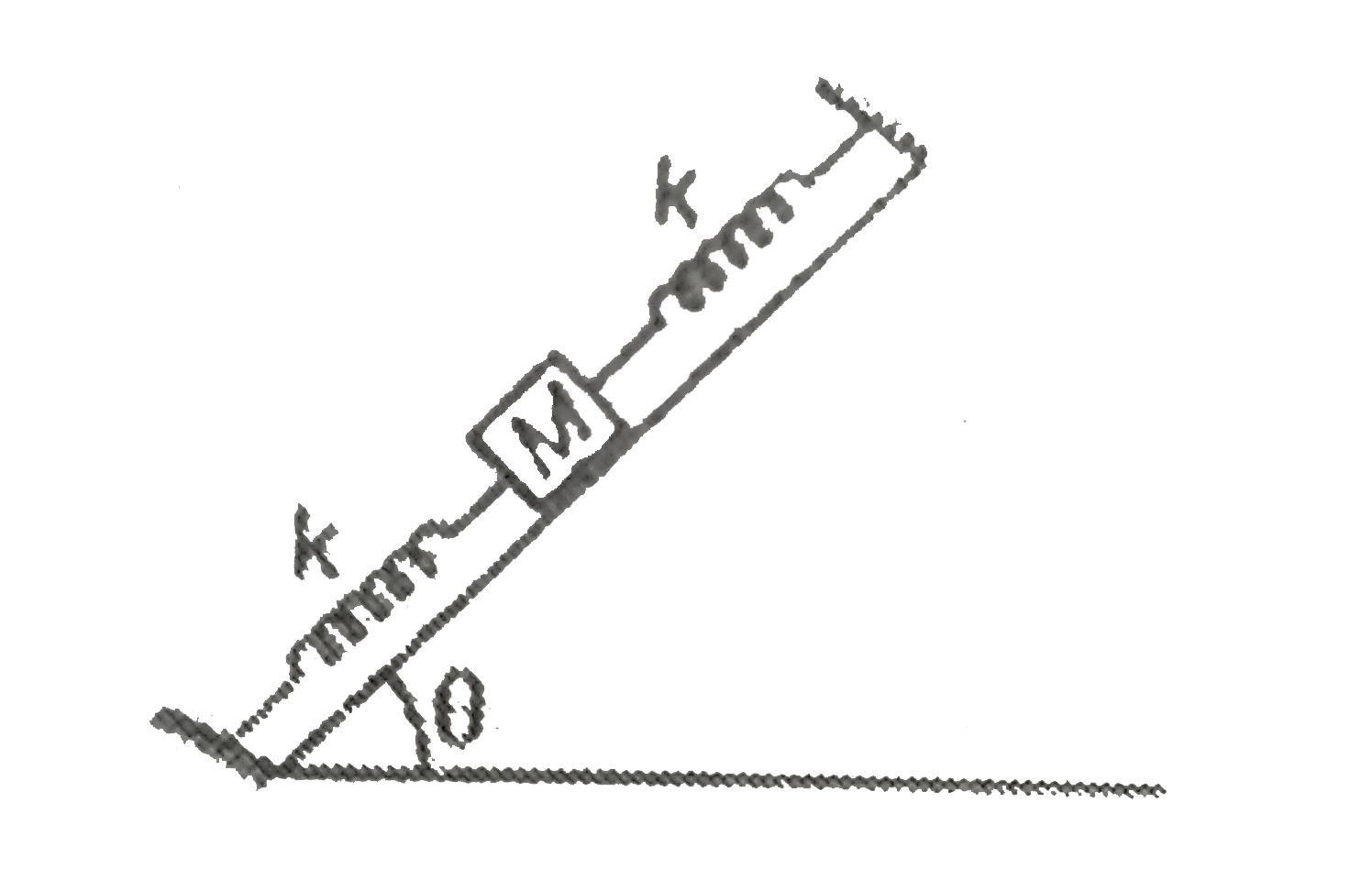
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionAn object suspended from a spring exhibits oscillations of period `T`. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
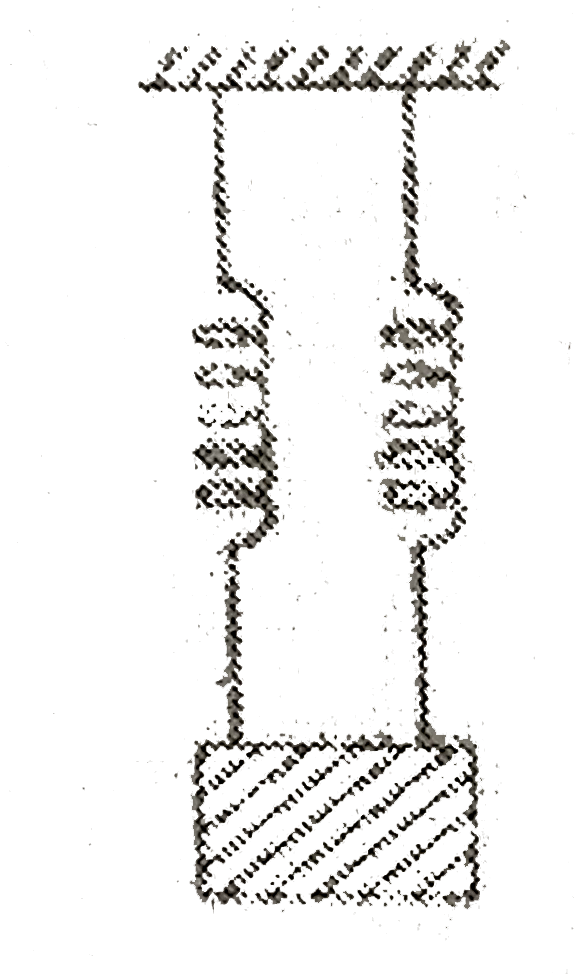
View SolutionA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be

View SolutionThe potential energy of a harmonic oscillator of mass 2 kg in its mean positioin is 5J. If its total energy is 9J and its amplitude is 0.01m, its period will be
View SolutionLet `T_(1)` and `T_(2)` be the time periods of two springs A and B when a mass m is suspended from them separately. Now both the springs are connected in parallel and same mass m is suspended with them. Now let T be the time period in this position. Then
View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resulting amplitude is equal to the amplitude of individual motions, the phase difference between them is
View SolutionA ball of mass 2kg hanging from a spring oscillates with a time period `2pi` seconds. Ball is removed when it is in equilibrium position, then spring shortens by
View SolutionA simple pendulum 4 m long swings with an amplitude of 0.2 m. What is its acceleration at the ends of its path? (g = `10m//s^(2)`)
View SolutionTwo simple harmonic motions `y_(1) = Asinomegat` and `y_(2)` = Acos`omega`t are superimposed on a particle of mass m. The total mechanical energy of the particle is
View SolutionThe maximum acceleratioin of a particle in SHM is made two times keeping the maximum speed to be constant. It is possible when
View SolutionDisplacement-time equation of a particle executing SHM is x=4sin`omega`t+3tsin(omegat+pi//3)`
Here, x is in cm and t ini sec. The amplitude of oscillation of the particle is approximately.
View SolutionFrequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/`s^(2)`
View SolutionA pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance `(3l)/4`. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
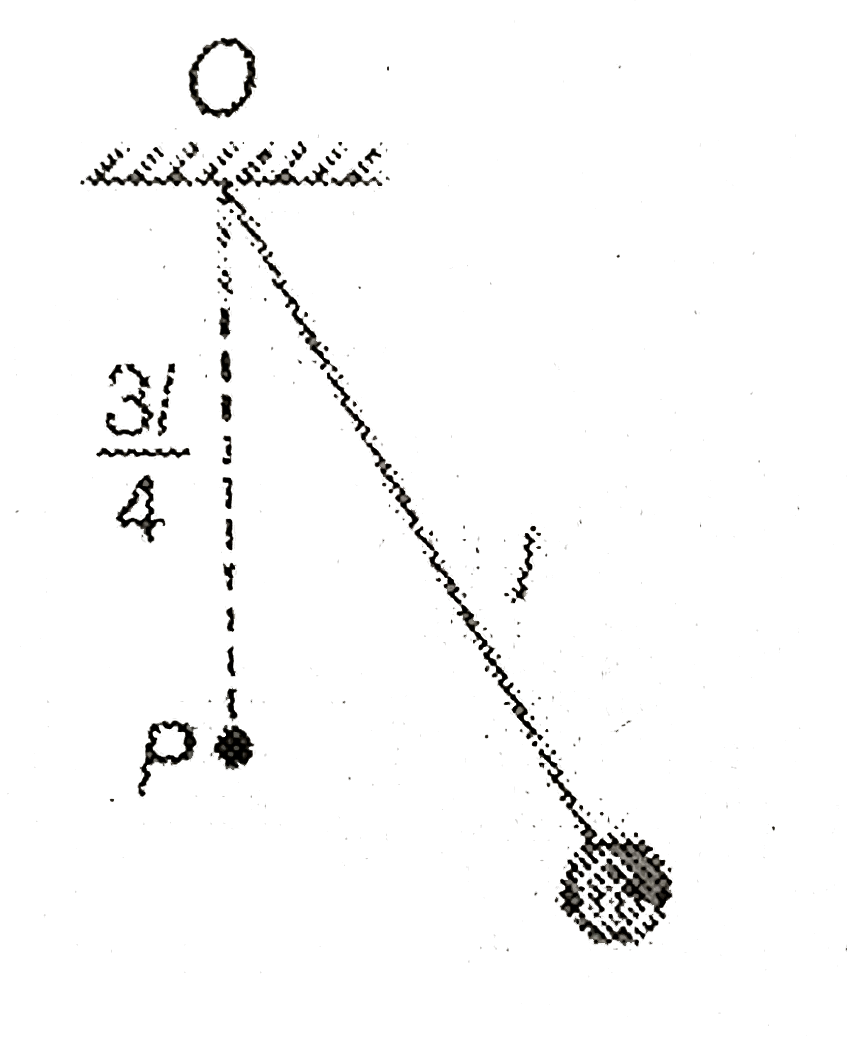
View SolutionA particle moves according to the law, `x=acos(pit//2).` . What is the distance covered by it in time interval `t=0` to `t=3` second.
View SolutionTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
View SolutionMaximum velocity in SHM is `v_(m)`. The average velocity during motion from one extreme point to the other extreme point will be
View SolutionAn object of mass `0.2 kg` executes simple harmonic oscillation along the `x`-axis with a frequency `(25)/pi`. At the position `x = 0.04m`, the object has kinetic energy of `0.5 J` and potential energy of `0.4 J`. The amplitude of oscillation is (potential energy is zero at mean position)
View SolutionThe potential energy of a particle of mass 1 kg `U = 10 + (x-2)^(2)`. Herer, U is in joule and x in met. On the positive x=axis particle travels up to x=+6cm. Choose the wrong statement.
View SolutionA cylinderical block of wood of mass m and area cross-section A is floating in water (density = `rho`) when its axis vertical. When dressed a little and the released the block starts oscillating. The period oscillations is
View SolutionThe displacement of two identical particles executing SHM are represented by equations.
`x_(1) = 4sin(10t+pi/6)` and `x_(2)=5cosepsilont`
For what value of epsilon of both the particles is same?
View SolutionA simple pendulum has time period T = 2s in air. If the whole arrangement is placed in a non viscous liquid whose density is 1/2 times the density of bob. The time period in the liquid will be
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density `rho`. If it is givan a small vertical displacement from equilibrium, it undergoes oscillation with a time period T, then select the wrong alternative.
View SolutionFour simple harmonic vibrations `x_(1) = 8sinomegat`, `x_(2) = 6sin(omegat+pi/2)`, `x_(3)=4sin(omegat+pi)` and `x_(4) = 2sin(omegat+(3pi)/2)` are superimposed on each other. The resulting amplitude and its phase difference with `x_(1)` are respectively
View SolutionAn assembly of identicl spring mass system is placed on a smooth horizontal surface as shown. Initially the springs are relaxed. The left mass is displaced to the left while the right mass is displaced to the right and released. The resulting collision is elastic. The time period of the oscillatins of the system is.
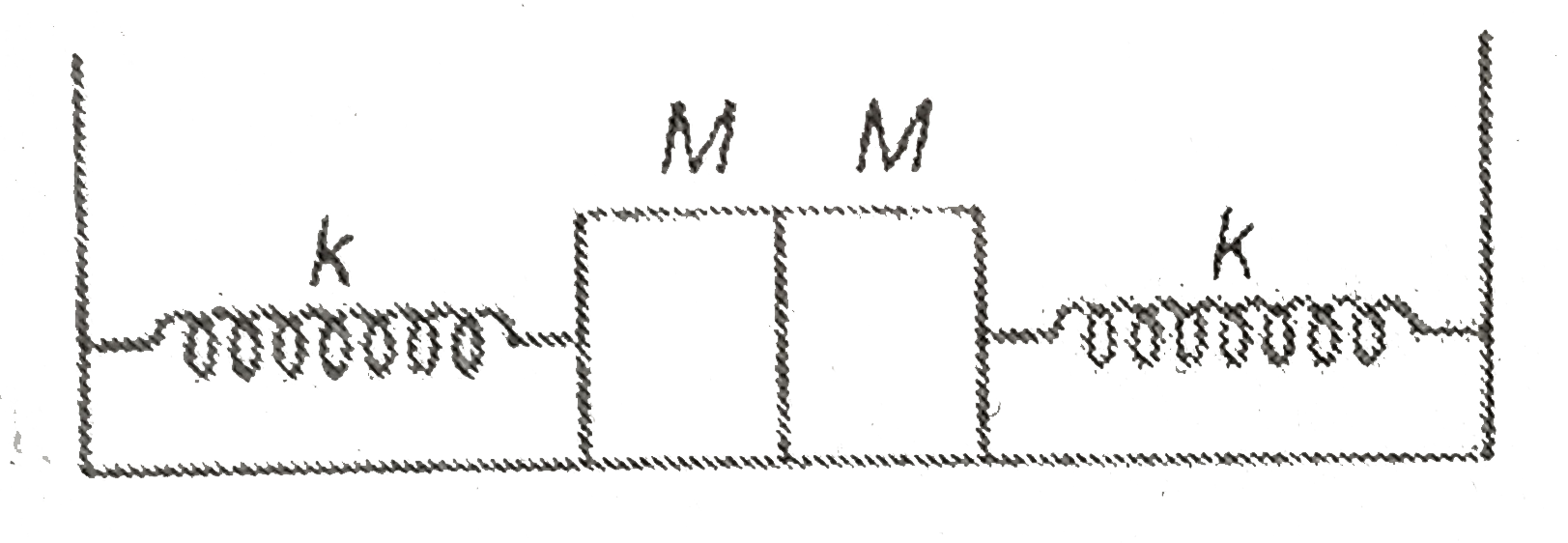
View SolutionA body is executing simple harmonic motion. At a displacement x (from its mean position) its potential energy is `E_(1)` and at a displacement y its potential energy is `E_(2)`. The potential energy is E at displacement (x+y) . Then:
View SolutionTwo springs with negligible massess and force constant of `k_(1)= 200 Nm^(-1)` and `k_(2)=160Nm^(-1)` are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position ir. Which both springs are neither stretched nor compressed. At time t = 0, sharp impulse of 50 N-s is given to the block in horizontal direction.
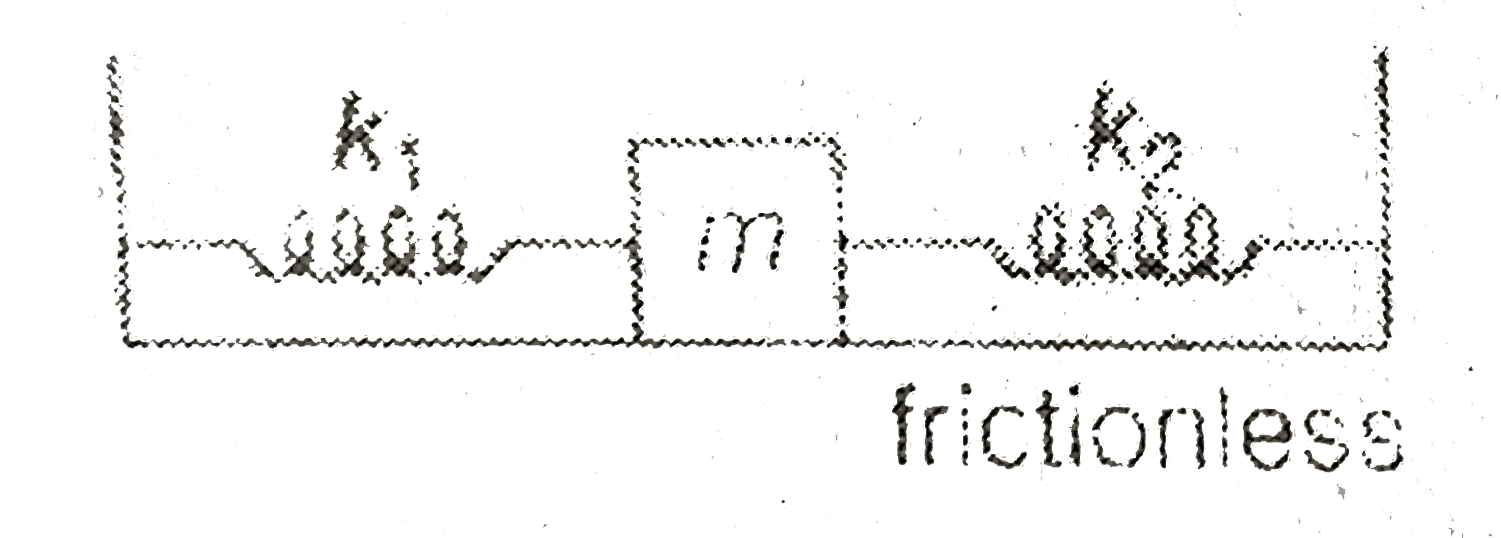
View SolutionThe potential energy of a harmonic oscillator of mass 2kg in its equilibrium position is 5 joules. Its total energy is 9 joules and its amplitude is 1cm. Its time period will be
View SolutionA vehicle is moving on a circular path of radius R with constant speed `sqrt(gR)`. A simple pendulum of length l hangs from the ceilling of the vehicle. The time period of oscillations of the pendulum is
View SolutionTwo simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
View SolutionA horizontal spring mass system is executing SHM with time period of 4s. At time t=0, it is at mean position. Find the minimum time after which its potential energy becomes three times of kinetic energy.
View Solution
Only one question is correct questions and complete solutions for chapter SIMPLE HARMONIC MOTION of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY MASTER PROBLEM PACKAGE Class 11 PHYSICS SIMPLE HARMONIC MOTION
- Comprehension types
- Example Type 1
- Example Type 10
- Example Type 11
- Example Type 12
- Example Type 13
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Example Type 7
- Example Type 8
- Example Type 9
- Examples
- Exercise 14.1
- Exercise 14.2
- Exercise 14.3
- Exercise 14.4
- Integer type questions
- Intro. Exer.
- JEE Advanced
- Level 1 Assertion And Reason
- Level 1 Single Correct
- Level 1 Subjective
- Level 2 Comprehension
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Matrix matching type questions
- Miscellaneous Examples
- More than one option is correct
- Only one question is correct