Complete Solutions to Exercises of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| HC VERMA | Exercises |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
The surface of water in a water tank on the top of a house is 4 m above the tap level. Find the pressure of water at the tap, above atmospheric pressure, when the tap is closed. Is it necessary to specify that the tap is closed? Take `g=10ms^-2`
View SolutionThe heights of mercury surfaces in the tow arms of the manometer shown in figure are 2 cm and 8cm. Atmospheric pressure `=1.01xx10^5Nm^-2` . Find a. the pressure of the gas in the cylinder and b. the pressure of mercury at the bottom of the U tube.

View SolutionThe area of cross section of the wider tube shown in figure is `900 cm^2`. If the boy standing on the piston weights 45 kg, find the difference in the levels of water in the two tubes.

View SolutionA glass full of water has a bottom of area `20 cm^(2)`, top of area `20cm^(2)`, height `20 cm` and volume half a litre.
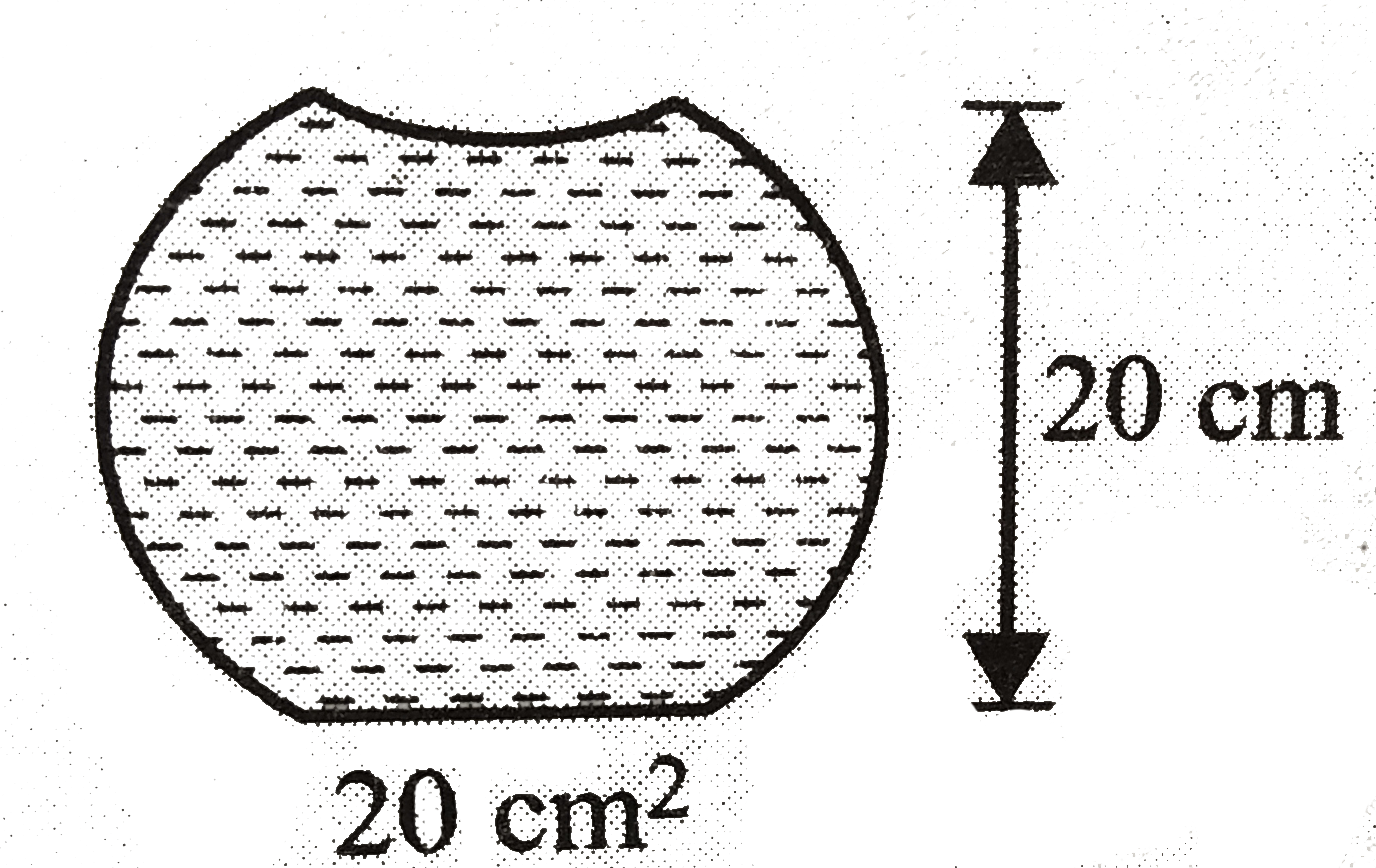
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the water. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure `= 1.0 xx 10^(5) N//m^(2)`. Density of water `= 1000 kg//m^(-3)` and `g = 10 m//s^(2)`
View SolutionSuppose the glass of the previous problem is covered by a jar and air inside the jar is completely pumped out a. What will be the answer to the problem? b.Show that the answers do not change if a glass of different shape is used provided the height, the bottom area and the volume are unchanged.
View SolutionIf water be used to construct a barometer, what would be the height of water column at a standard atmospheric presure (76cm of mercury)?
View SolutionFind the force exerted by the water on a `2m^2` plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface? Neglect the size of the stone in comparison to the depth of the sea.
View SolutionWater is filled in a rectangular tank of size `3mxx2mxx1m`. a. Find the total force exerted by the water on the bottom surface of the tank. b. cosider a vertical side of area `2mxx1m`. Take a horizontal strip of wide `deltax` metre in this side, situated at a depth of x metre from the surface of water. Find the torque of the force calculate in part b. about the bottom edge of this side. e. Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take `=10ms^-2`.
View SolutionAn ornament weighting 36 gin air, weighs ony 34 g in water. Assuming that some copper is mixed wilth godl to prepare the ornament, find the amount of coper in it. Specific gravity of godl is 19.3 and that of copper is 8.9.
View SolutionRefer to the previous problem. Suppose, the goldsmith argues that he has not mixed copper or any other material with gold, rather some cavities might have been left inside the ornament. Calcuate the weighs given in that problem.
View SolutionA metal piece of mass 160 g lies iln equilibrium inside a glass of water figure. The ppece touches the bottom of the glass at a small number of points. If the density of the metl is 8000 kg `m^-3`, find the normal fore exerted by the bottom of the glass on the metal piece.

View SolutionA ferry boat has internal volume `1m^3` and weight 50 kg. a. Neglecting the thickness of te wood, find the fraction of the volume of the boat immersed in water. b.If a leak develpops n the bottom and water starts coming in, what fraction of the boat's volume will be filled with water before water starts coming in from the sides?
View SolutionA cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
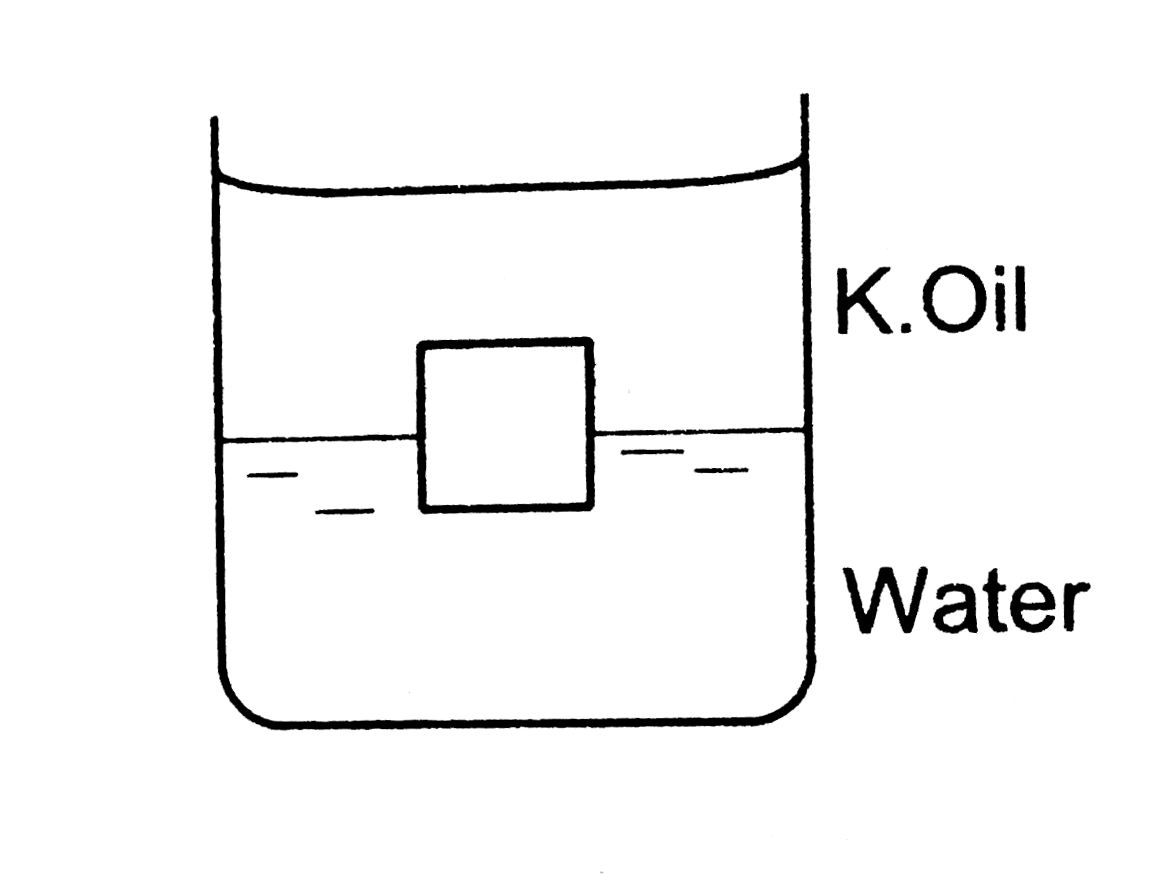
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 nd that of ice is 0.9.
View SolutionA cubical box is to be constructed with irogn sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron `=8000kg m^-3`and density of water `=1000 kgm^-3`.
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just alow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View SolutionSolve the prievious problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
View SolutionA solid sphere of radius 5 cm floats in water. If a maximum load of 0. kg can be put on it withot wetting the load find the specific gravityof the material of the sphere.
View SolutionFind the ratio of the weights as measured by a spring balance, of a 1 kg block of iron nd a 1kg block of wood. Density of iron `=7800 kg m^-3` density of wood `=800 kg m^-3 and density of air =1.293 kgm^-3`.
View SolutionA cylindrical object of outer diameter 20 cm and mass 2 kg flots in wter with its axis vertical. If it si lightly depressed and then released, find the time peiod of the resulting simple harmonic motion of the object.
View SolutionA cylindrical object of outer diameter 20 cm height 20 cm and density 8000 `kgm^-3` is supported by a vertical spring and is half dipped in water as shown in figue. a. Figure the elongation of the spring in equilibrium condition. b. If the object is sllightlly depressed and relation, find the time period of resulting oscillations of the objcet. The spring constant `=500 Nm^-1`.

View SolutionA wooden block of mass 0.5 kg and density 800 `kgm^-3` is fastened to the free end of a vetical spring of spring cosntant 50 N`m^-1` fixed at the bottom. If the entire system is completely immersed in water, find a. the elongation (or compresion) of the spring in equilibrium and b. the time period of vertical oscillations of het block when it is slightly depressed and released.
View SolutionAn ice cube of edge a is placed in an empty cylindrical vessel of radius 2a. Find the edge (in cm) of ice cube when it just leaves the contact with the bottom assuming that ice melts uniformly maintaining its cubical shape. Take a = 12 `pi` cm (Ice is lighter than water)
View SolutionA U-tube containing a liquid is accelerated horizontally with a constant acceleration `a_0`. If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.
View SolutionAt Deoprayag (Garhwal, UP) river Alaknanda mixes with the river Bhagirathi and becomes river Ganga. Suppose Alaknand has a width of 12 m, Bhagirathi has a width of 8m and Ganga ha sa width of 16m. Assume that the depth of water is same in the three rivers. Let the average speed of water in Alaknanda be `20 kmh^-1` and in Bhagirathi be `16 kmh^-1`. Find the average speed of water in the river Ganga.
View SolutionWaster flows throgh a horizontal tube of variable cross section.The area of cross section at A and B are 4 `mm^2 and 2mm^2` respectively. If 1 cc of water enters per seconds through. A find a. The speed of water at A, b. the speed of river at B and c. the pressure difference `P_A-P_B`.

View SolutionSuppose the tube in the previous problem is kep vertical with A upward but the other conditions remain the same. The separation between the cross sections at A and B is 15/16 cm. Repeat parts a., b, and c of the previous problem. `take g=10ms^-2`.
View SolutionSuppose the tube in the previous problem is kept verticla with B upward. Water enters through B at the rate of `1cm^3s^-1`. Repeat parts a, b, and c. Note that the speed decreases as the water falls down.
View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are `1cm^2 and 0.5 cm^2` respectively. The height difference between A and B is 5m. If the speed of water at A is 10 `cms^-1` find a the speed at B and b the difference in pressures at A and B.

View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are `4cm^2 and 2cm^2` respectively, find the rate of flow of water across any section.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are `5cm^2 and 2cm^2` respectively. The rate of flow of water through the tube is `500 cm^3s^-1` . Find the difference of mercury levels in the U-tube.

View SolutionWater leaks out from an open tank through a hole of area `2mm^2` in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tankis `0.4 m^2`. The pressure at the open surface and the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. a. Find the initial speed of water coming out of the hole. b. Findteh speed of water coming out when half of water has leaked out. c. Find the volume of water leaked out during a time interval dt after the height remained is h. Thus find the decrease in height dh in term of h and dt.
d. From the result of part c. find the time required for half of the water to leak out.
View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.

View Solution
Exercises questions and complete solutions for chapter FLUID MECHANICS of HC VERMA PHYSICS (HINGLISH) of Class 11