A glass full of water has a bottom of area , top of area , height and volume half a litre.
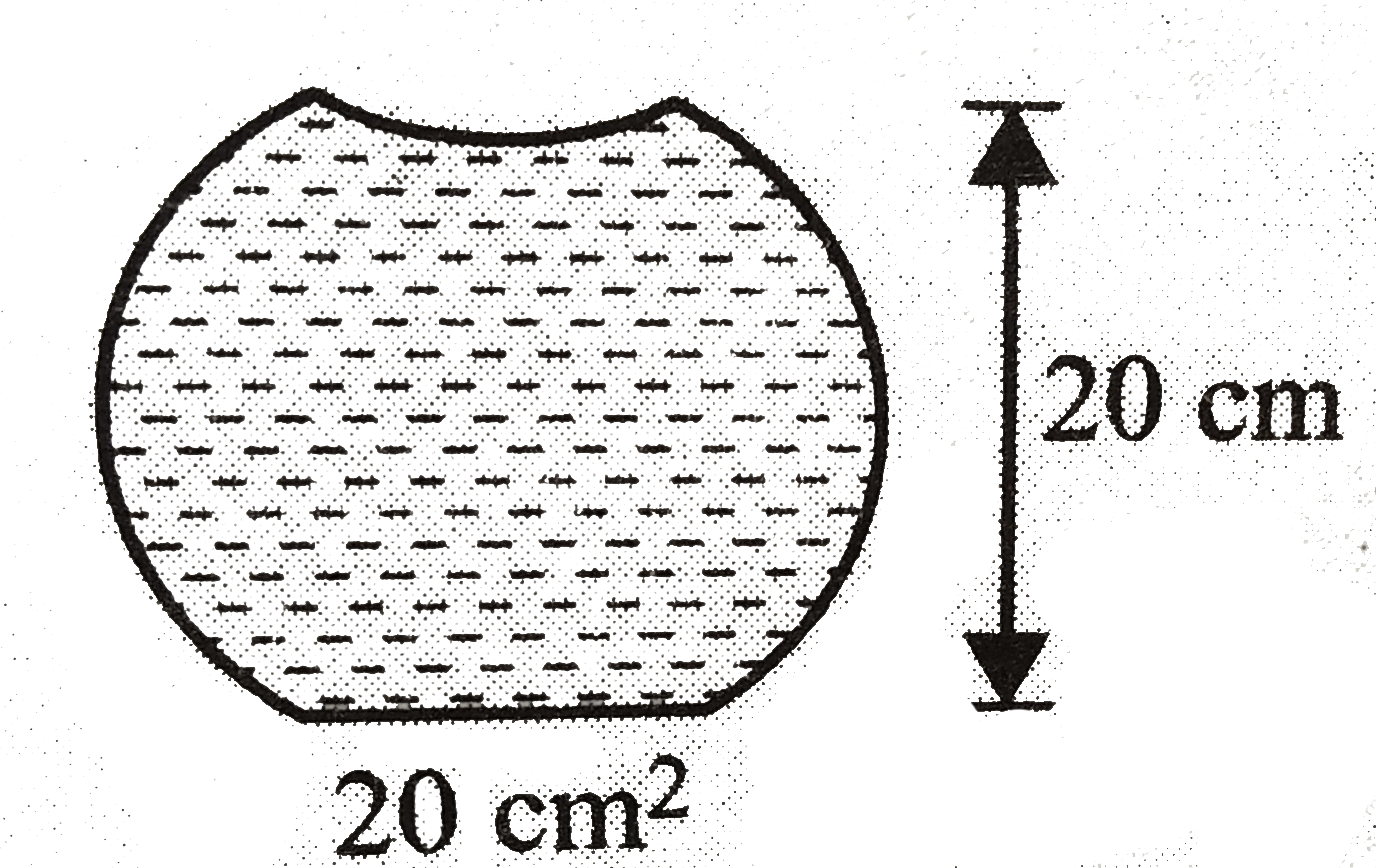
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the water. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure . Density of water and
The correct Answer is:A, B, D
,
g=10m/s^2v=500m/=500g=0.5kg=AxxhxxP_wxxg+P_axxA=A(hrho_wg+P_a)=204NP_axxA+mg=Axxhxxrho_2xxg+F_s+P_axxArarr mg=Axxhxxp_wxg+F_srarr 0.5xx1=20xx10^-4xx20x10^-2xx10^-3xx10+F_srarr F_s=5-4=1N (upward)
This force 1N is provided by the sides of the glass.
Topper's Solved these Questions
Similar Questions
A glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
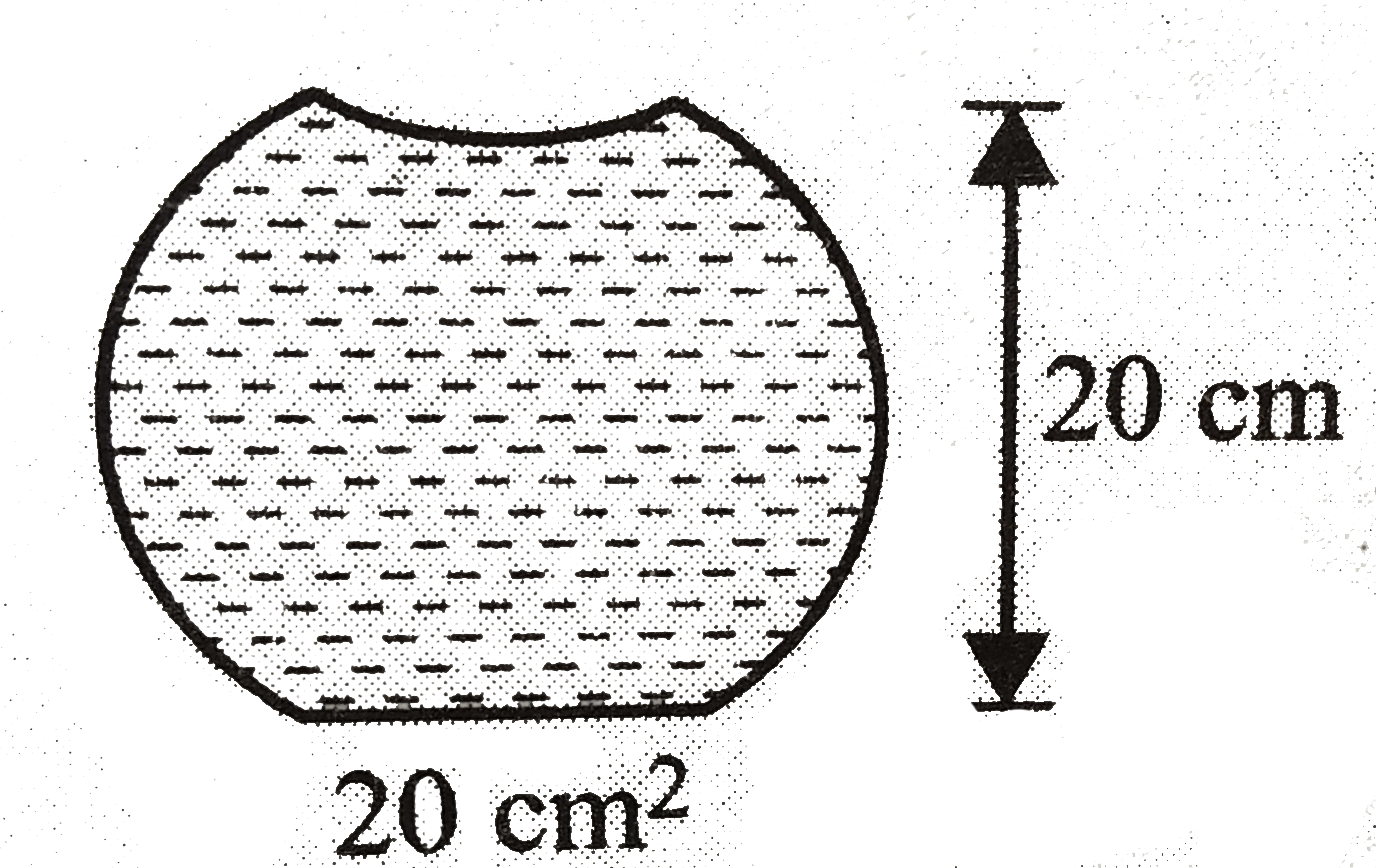
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View Solution
Knowledge Check
In the above question, the resultant upward force exerted by the sides of the glass on the water is
A100 NB102 NC303 ND211 NA glass of water upto a height of 10 cm has a bottom of area 10cm2 , top of area 30cm2 and volume 1 litre. The downward force exerted by water on the bottom is…(Taking g=10m/s2 ,density of water =103kg/m3 , atmosphereic pressure =1.01×105N/m2)
A100 NB102 NC110 ND120 NFind the force acting on the pistion of 3cm2 at point 2 due to the water coluum of height 10m.
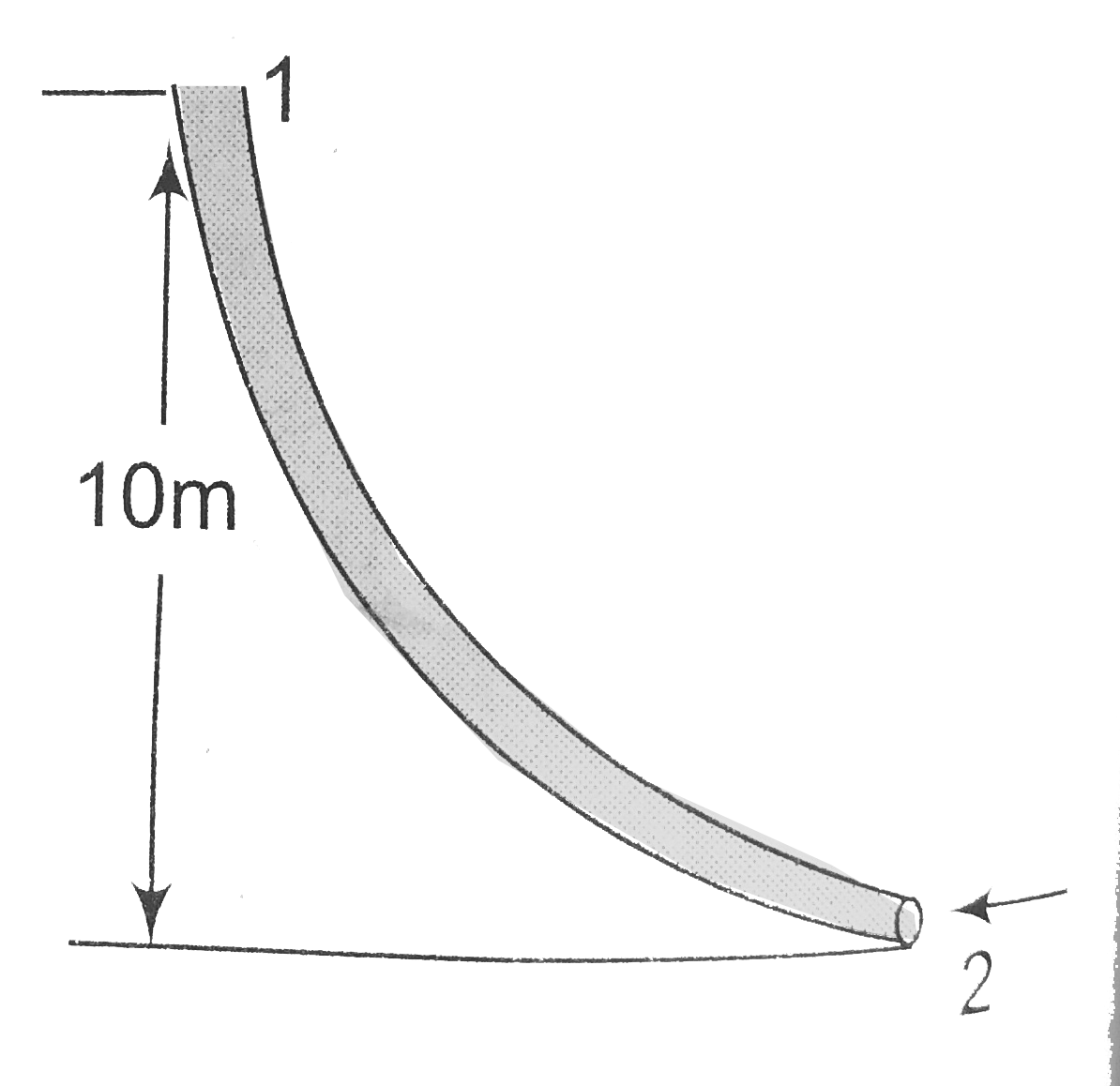 A10 NB20 NC30 ND40 N
A10 NB20 NC30 ND40 N
A glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View SolutionA beaker of circular ceross sectionof radius 4 cm is filled with mercury up to a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmospheric pressure =105Nm−2. Density of mercury =13600kgm−3.Takeg10ms−2
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View Solution
