Complete Solutions to SELECTED PROBLEMS of chapter DYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DYNAMICS |
| S CHAND | SELECTED PROBLEMS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
What is the distance in km of quasar from whigh light takes 3 billion years to reach us? `c=3xx10^(5)` km/s.
View SolutionA train 100m long is moving with a speed of `72 kmh^(-1)`. Calculate the time taken by the train to cross a bridge `0.5 km` long?
View SolutionA man walks on a straight road from his home to market 2.5 km away with speed of 5 km/h Finding the market closed, he instantly turns and walks back with a speed of 7.5 km/h. What is the magnitude of average velocity and average speed of the man over the interval of time (i) 0 to 30 min (ii) 0 to 50 min (iii) 0 to 40 min ?
View SolutionA man walks on a straight road from his home to market 2.5 km away with speed of 5 km/h Finding the market closed, he instantly turns and walks back with a speed of 7.5 km/h. What is the magnitude of average velocity and average speed of the man over the interval of time (i) 0 to 30 min (ii) 0 to 50 min (iii) 0 to 40 min ?
View SolutionTwo straight lines drawn on the same displacement time graph make angles `30^(@)" and "60^(@)` with time axis respectively. Which line represents greater velocity? What is the ratio of the two velocities?

View SolutionA body travels a distance `x_1` with velocity `v_1` and distance `x_2` with velocity `v_2` in the same direction. What is the average velocity of the body?
View SolutionThe north American and European continents are drifting apart at an average speed of about 3cm per year. At this speed how long (in years) will it take for them to drift apart by another 1500m?
View SolutionWhen a person sneezes his eyes remain shut for about `0.5s`. If the person is driving a race car at 108 km/hr how far does it move during that time?
View SolutionThe velocity of a bullet is reduced from `150 ms^(-1)" to "100 ms^(-1)` while travelling through a wooden plank of thickness 50 min. Find the retardation assuming it to be unifrom.
View SolutionA particle starts with a velocity of `200 cm"/"s` and moves in a straight line with a retardation of `10 cm"/"s^(2)`. Find the time it takes to describe 1500 cm and explain the double answer.
View SolutionA car A is travelling on a straight level road with a uniform speed of a 60 km/h. It is followed by another car B which is moving with a speed of 70 km/h. When the distance between them is `2.5 km`, the car B is given a decceleration of `20 km"/"h^(2)`. After what distance and time will B catch up with A?
View SolutionThe speed of a train is reduced from 60km/h to 15 km/h, while it travels a distance of 450m. If the retardation is uniform, find how much further it will travel before coming to rest?
View SolutionA rocket is fired vertically up from the ground with a resultant vertical acceleration of `10 m//s^2.` The fuel is finished in 1 min and it continues to move up. (a) What is the maximum height reached? (b) Afte2r how much time from then will the maximum height be reached?(Take `g= 10 m//s^2`)
View SolutionA body starting from rest was observed to cover 20m in one second and 40m during the next second. How far the body travelled before the first observation was taken?
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute the maximum velocity aquired by the car is
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionBrakes are applied to a train travelling at 72 km/h. After passing 200m its velocity is reduced to 36 km/h. At the same rate of retardation how much further will it go before it is brought to rest?
View SolutionStarting from rest a car moves with uniform acceleration and attains a velocity of 72 km/h in 15s. It then moves with uniform speed for 20 s and is then brought to rest in 10 s under uniform retardation. Find the total distance travelled using velocity time graph.
View SolutionA motor car starts from rest and accelerates uniformly for 10s to a velocity of `8 m"/"s`. It, then runs at a constant velocity and is finally brought to rest in 53 m with a constant retardation. The total distance passed over is 584 m. Find the value of acceleration, retardation and the total time taken.
View SolutionA ball rolls down an inclined track 2 m long in 4s. Find
Acceleration.
View SolutionA ball rolls down an inclined track 2 m long in 4s. Find
The time taken to cover the second metre of the track.
View SolutionA ball rolls down an inclined track 2 m long in 4s. Find
Speed of the ball at the bottom of track.
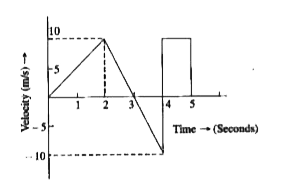
View SolutionThe velocity-time graph of a particle moving along a straight line is shown in Fig. 4.1.32. Calculate the distance travelled by the particle in the interval between t = 0 and t = 5s?
View SolutionThe velocity-time graph of a particle moving along the x-axis is as shown in Fig. 4.1.33. Calculate
The acceleration.
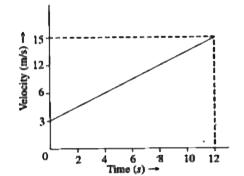
View SolutionThe velocity-time graph of a particle moving along the x-axis is as shown in Fig. 4.1.33. Calculate
The distance travelled and the displacement of the particle in 10 s.

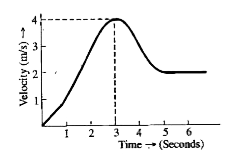
View SolutionThe velocity-time graph of a particle starting from rest and moving along a straight line is as shown in Fig. 4.1.34
What is the average acceleration for the interval t = 0 to t = 3-0 s ?
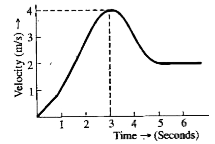
View SolutionThe velocity-time graph of a particle starting from rest and moving along a straight line is as shown in Fig. 4.1.34
When is the acceleration zero ?
View SolutionThe velocity-time graph of a body projected vertically upwards is as shown in Fig. 4.1.35 Calculate
The displacement of the body in the interval 0 to 3 s.
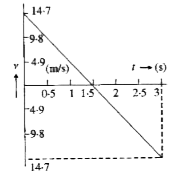
View SolutionThe velocity-time graph of a body projected vertically upwards is as shown in Fig. 4.1.35 Calculate
The distance travelled during the same interval.
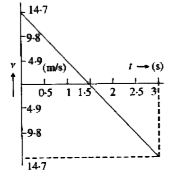
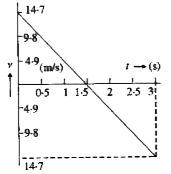
View SolutionThe velocity-time graph of a body projected vertically upwards is as shown in Fig. 4.1.35 Calculate
The acceleration of the body.
View SolutionA particle moves along a straight line such that its displacement at any time t is given by `s = (t^(3)-6t^(2)+3t +4)m`
The velocity when the acceleration is zero, is
View SolutionThe acceleration a in `ms^-2` of a particle is given by `a=3t^2+2t+2`, where t is the time. If the particle starts out with a velocity `v=2ms^-1` at `t=0`, then find the velocity at the end of `2s`.
View SolutionThe deceleration exerienced by a moving motor blat, after its engine is cut-off is given by `dv//dt=-kv^(3)`, where `k` is constant. If `v_(0)` is the magnitude of the velocity at cut-off, the magnitude of the velocity at a time `t` after the cut-off is.
View SolutionA stone is projected vertically upwards with a velocity of `19.6 m"/"s`. Find
The maximum height attained.
View SolutionA stone is projected vertically upwards with a velocity of `19.6 m"/"s`. Find
The time of ascent.
View SolutionFrom the top of a tower of height of 44.1 m, a stone is dropped. How long does it take and what is its velocity when it reaches the ground ?
View SolutionA ball thrown up is caught back by the thrower after 4 seconds. How high did it go and with what velocity was it thrown ? How far below its highest point was it 3 s after start ?
View SolutionA stone is projected vertically upwards with a velocity of `19.6 m"/"s` from the top of a tower 20.4 m height. Find
The greatest elevation.
View SolutionA stone is projected vertically upwards with a velocity of `19.6 m"/"s` from the top of a tower 20.4 m height. Find
Its velocity at the moment it strikes the ground.
View SolutionA stone is allowed to fall from the top of a tower 300 m high and at the same time another is projected vertically upward with a velocity of `75 m"/"s`. Find when and where the two will meet ?
View SolutionFor stone freely falling from rest, the distance covered by it in the last second is equal to the distance covered by it in the first three seconds. Calculate the time taken by the stone to reach the ground.
View SolutionStones are thrown upwards one after the other with the same speed at an interval of 1 s. The next stone is thrown when the velocity of the previous stone is zero. Calculate the maximum height attained by the stone.
View SolutionA man in a balloon rising vertically with an acceleration of `4.9 m "/" s^(2)`, releases a ball 2 s after the balloon is let go from the ground. Calculate the greatest height above the ground reached by the ball.
View SolutionA packet is dropped from a balloon rising up with uniform velocity `9.8 "ms"^(-1)`. If the balloon is at a height of 39.2 m from the ground at the time of dropping the stone, the stone reaches the ground after
View SolutionA parachutist, after bailing out falls a distance of 19.6 m after which the parachute opens and he decelerates at `1.1 m"/"s^(2)`. He reaches the ground with a speed of `2 m"/"s^(2)`. Find
How long the parachute was in air ?
View SolutionA parachutist, after bailing out falls a distance of 19.6 m after which the parachute opens and he decelerates at `1.1 m"/"s^(2)`. He reaches the ground with a speed of `2 m"/"s^(2)`. Find
At what height did he bail out ?
View SolutionA bomb is dropped from an aircraft when it is directly above a target at a height of 1000 m. The aircraft is moving with a velocity of 500 km/hr. Will the bomb hit the target, if not, by how much distance it will miss the target ?
View SolutionAn elevator in which a man is standing is moving upwards with a constant speed of `10 m"/"s`. If the man drops a ball from a height 2.45 m, find the time taken by it to reach the floor of the elevator.
View SolutionA ball dropped from a cliff travel 34.3 m in the last second before it reaches the ground at the foot of the cliff. Find the height of the cliff?
View SolutionTwo balls are thrown simultaneously, A vertically upwards with a speed of 20 m/s from the ground, and B vertically downwards from a height of 40 m with the same speed along the same line of motion. At what point do the two balls collide? Take `g = 9.8 m//s^(2)`.
View SolutionA stone is dropped from the top of a tower. One second later another stone is dropped from a point 25 m below the top. The stones reach the ground simultaeously. Calculate the height of the tower.
View SolutionA jet airplane travelling at the speed of `500 km h^(-1)` ejects its products of combustion at the speed of `1500 km h^(-1)` relative to the jet plane. What is the speed of the latter with respecct to an observer on the ground ?
View SolutionTow railway tracks are parallel to west-east direction. Along one track train A moves with a speed of `30 ms^(-1)` from west to east, while along the second track, train B moves with a speed of `48 ms^(-1)` from east to west. Calculate
Relative speed of B w.r.t. A .
View SolutionTow railway tracks are parallel to west-east direction. Along one track train A moves with a speed of `30 ms^(-1)` from west to east, while along the second track, train B moves with a speed of `48 ms^(-1)` from east to west. Calculate
Relative speed of ground w.r.t. B.
View SolutionTwo parallel rail tracks run noth-south. Train A moves north with a speed of `54 kmh^(-1)` and train B moves south with a speed of `90 kmh^(-1)`. What is
Relative velocity of B respect to A.
View SolutionTwo parallel rail tracks run noth-south. Train A moves north with a speed of `54 kmh^(-1)` and train B moves south with a speed of ` 90 kmh^(-1)`. What is
Relative velocity of ground with respect to B.
View SolutionTwo parallel rail tracks run noth-south. Train A moves north with a speed of `54 kmh^(-1)` and train B moves south with a speed of `90 kmh^(-1)`. What is
Velocity of a monkey running the roof of the train A against its motion (with a velocity of `18 kmh^(-1)` with respecct to the train A) as observed by a man standing on the ground?
View SolutionTwo towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man ccling with a speed of `20 km h^(-)` in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the oppsite direction. What is the period T of the bus service and with what speed (assi,ed cpmstant) do the buses ply on the rod?
View SolutionA scooter is travelling on a straight road with a speed of ` 30 kmh^(-1)` behind the scooter, there is a car travelling at a speed of `45 kmh^(-1)`. When the distance between them is 7.5 km the car is given an acceleration of `15 kmh^(-2)`. After what distance and time with the car catch the scooter?
View SolutionAt the sight of green signal, a car starts with a uniform acceleration of `4 ms^(-1)` overtakes and passes the car
At what distance from the starting point will the car overtake the bus.
View SolutionAt the sight of green signal, a car starts with a uniform acceleration of `4 ms^(-1)` overtakes and passes the car
How fast will the car be travelling at that instant ?
View SolutionA bomb is dropped from an acroplane flying horizontally with a velocity of `720 km "/"h` at an altitude of 980 m. After what time, the bomb well it the ground.
View SolutionA body is thrown horizontally from the top of a tower `44.1 m` high strikes the ground at an angle of `45^(@)` with the hoizontal. Find the speed with which it was thrown from the top?
View SolutionA ball is projected horizontally with a velocity of `3 ms^(-1)`. What is the velocity of the ball after `0.4 ms^(-1)` ? [`g = 10 ms^(-2)`].
View SolutionA projectile is fired horizontally with a velocity of `98 ms^(-1)` from the top of a hill 490 m high. Find
The time taken to reach the ground.
View SolutionA projectile is fired horizontally with a velocity of `98 ms^(-1)` from the top of a hill 490 m high. Find
The distance of the target from the hill.
View SolutionA projectile is fired horizontally with a velocity of `98 ms^(-1)` from the top of a hill 490 m high. Find
The velocity with which the body will strike the ground.
View SolutionAn aeroplane moving horizontally with a speed of `180 km "/"hr` drops a food packet while flying at a height of 490 m. Find the horizontal range.
View SolutionFrom the top of a tower `29.4 m` high a body is projected downwards at an angle of `30^(@)` to the horizontal, with a velocity of `9.8 m "/"s`. How long will it take before striking the ground ?
View SolutionAn aeroplane moving horizontally at `20 ms^(-1)` drops a bag. What is the displacement of the bag after 5 second ? `[g = 10 ms^(-2)]`.
View SolutionThe height y and the distance x along the hoizontal plane of the projectile on certain planet (with no surrouding atmosphere) are given by `y = (8t - 5 t^(2))m " and "x = 6t m`, where t is second. Calculate the velocity with which the projectile is projected.
View SolutionA plane is flying horizontally at `98 m"/"s` and releases an object which reaches the ground in 10 s. Find the angle made by it while hitting the ground.
View SolutionTwo tall buildings are 45 m apart. With what velocity must a ball be thrown vertically from a window 50 m above the ground in one building so that it enters a window `5.9 m` above the ground in the other building.
View SolutionAn aeroplane is flying at a height of 3000 m above the ground level. If the angle subtended at ground observation point by the aeroplane position 12 s apart is `30^(@)`, what is the speed of the aeroplane ?
View SolutionA ball rolls off the top of a stairway with a horizontal velocity `v_(0) m"/"s`. If the steps are h metre high and b metre wide, show that the ball will hit the edge if `n = 2hv_(0)^(2)"/"gb^(2)`.
View SolutionA man throws a shot at an angle of `45^(@)` with the horizontal plane from a height of `1.5 m`. If the shot strikes the ground at a horizontal distance of 30 m, find the velocity of throw. `(g = 10 m "/"s^(2))`.
View SolutionA shell is fired at an angle of `30^(@)` to the horizontal with a velocity of `392 ms^(-1)`. Find the time of flight, horizontal range and the maximum height attained.
View SolutionA bullet fired at an angle `60^(@)` with the vertical the ground at a distance of 2 hm. Calculate the distance at which the bullet will hit the ground when fired at an angle of `45^(@)`, assuming the speed to be same.
View SolutionThe maximum range of a gun on a horizontal terrain is 16 km. If is `10 m"/"s^(2)`, find the muzzle velocity of the shell.
View SolutionA football is kicked off with an initial velocity of `9.8 m"/"s` at a angle `45^(@)` with the horizontal. The goalkeeper at a distance 38 m away in the direction of kick starts running to catch the ball at that instant. What must be his speed, if he is to catch the ball before it hits the ground ?
View SolutionA ball is thrown at an angle `theta` with the horizontal. Its time of flight is 2 second. Its horizontal range is 100 m. What is the horizontal component of the velocity of projection. `[g = 10 ms^(-2)]`
View SolutionA bullet is fired at an angle of `15^(@)` with the horizontal and hits the groun 6 km away. Is it possible to hit a target 10 km away by adjusting the angle of projection assuming the initial speed to be the same.
View SolutionIf 4 seconds be the time in which a projectile reaches a poit P of its path and 5 seconds the time from P till it reaches the horizontal plane through the point of projection, show that the height of P above the horizontal plane is 98 m.
View SolutionA ball is projected horizontally from the top of a building `19.6 m` high. If the line joining the point of projection to the point where it hits the ground makes an angle of `45^(@)` to the horizontal, what is the initial velocity of the ball?
View SolutionA ball is projected at an angle of `45^(@)`, above the horizontal, the horizontal range is 10 m.
What is the maximum height to which the ball rises ?
View SolutionA ball is projected at an angle of `45^(@)`, above the horizontal, the horizontal range is 10 m.
For the same intial speed what are the two angles of departure for which the range is 6 m ?
View SolutionA boy is able to throw a ball to a mazimum height of 30 m. What maximum distance can he throw the ball in a horizontal direction.
View SolutionA child throws a waterfilled bellon at an angle of `53.1^(@)` with a speed f `10 ms^(-1)`. A car is advancing towards the child with a constant speed of `5 ms^(-1)`, If the ballon is to hit the car, how far away should the car be when the ballon is thrown ?
View SolutionA particle is projected with a certain velocity so as to pass through a point at a horizontal distance R from the point of projection. Show that if `t_(1)` and `t_(2)` are the time taken to reach this point intwo possible ways in which the particle can be projected with the gicen veloity then `t_(1) t_(2) = R "/" g`.
View SolutionWind is blowing from the south at `10 m "/"s`, but to a cyclist it appears to be blwoing from the east at `10 m "/"s`. Determine the velocity of the cyclist in vector form.
View SolutionA eat is climbing a vertical pole with a speed of `4 m "/"s` and a dog is running towards the pole with a speed of `8 m "/"s`. What is the velocity of the dog relative to the eat ?
View SolutionA boat is moving with a velocity `3hati+4hatj` with respect to ground. The water in the river is moving with a velocity `-3hati-4hatj` with respect to the ground. Calculate the relative velocity of the boat with respect to water.
View SolutionTo a man walking at the rate of `2 km"/"h`, rain appears to fall verticall. When he doubles his speed, it appears to fall at `30^(@)` to the vertical. Find real speed and direction of rain.
View SolutionA ship is steaming north at `8sqrt 3 km"/"h` and a man walks across its deck in a direction due west at `8 km"/"h`. Find his resultant velocity in the ship.
View SolutionA train is accelerating towards noth at the rate of `4.9 m"/"s^(2)`. Find the acceleration of bolt which falls from the ceilling relative to
The train.
View SolutionA train is accelerating towards noth at the rate of `4.9 m "/"s^(2)`. Find the acceleration of bolt which falls from the ceilling relative to
To the Earth ?
View SolutionA person travelling eastwards finds the wind to blow from north. On doubling his speed, he finds it to come from north-east. Show that if he trebles his speed, the wind would appear to him to come from a direction making an angle `tan^(-1) (1/2)` north of east.
View SolutionOn a rainy day, the rain was falling vertically with a speed of `15 ms^(-1)`. A wind started blowing, with a speed of `5 m"/"s^(-1)` from north to south. In which direction should a girl waiting at a bus stop hold her umbrella ?
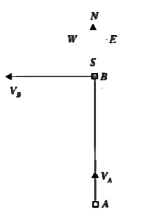
View SolutionFigure 4.2.30 shows two cars A and B, each running at a speed of `50 km"/"hr`. Initially they are along a straight line AB separated by a distance of 200 m, B is running towards west and A towards north. After how much time the separation between the cars will be the least and calculate by what distance they are separated. diromg tjeor closest approach ?
View SolutionA constant force acting on a body of mass 6kg changes its speed from `4 ms^(-1)" to "7ms^(-1)` in 50s. The direction of motion of the body remains unchanged. What is the magnitude and direction of force?
View Solution
SELECTED PROBLEMS questions and complete solutions for chapter DYNAMICS of S CHAND PHYSICS (ENGLISH) of Class 11