Complete Solutions to INTEGER TYPE QUESTIONS of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| NARAYANA | INTEGER TYPE QUESTIONS |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Under to action of constant force `F =10` N, a body moves in a straight line so that the relation between the distance `S` moved by the body and the time t is described by the equation `S =A -Bt +Ct^(2)` Find the mass of the body if `C =1 m//s^(2)` .
View SolutionBy what acceleration the boy must go up so that `100kg` block remains stationary on the wedge. The wedge is fixed and is smooth `(g =10m//s^(2))`
 .
.
View SolutionTwo blocks of mass 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 meter, see fig. The upper wire has negligible mass and the lower wire has a uniform mass of `0.2kg//m`. The whole system of blocks wires and support have an upward acceleration of `0.2m//s^2`. Acceleration due to gravity is `9.8m//s^2`.
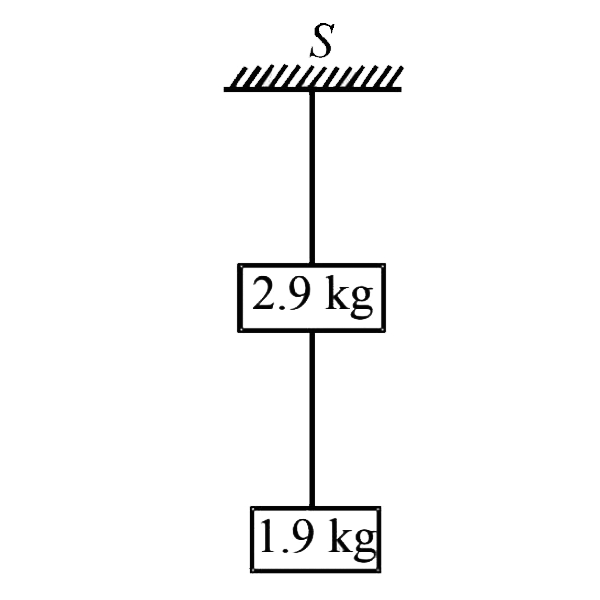
(i) Find the tension at the mid-point of the lower wire.
(ii) Find the tension at the mid-point of the upper wire.
View SolutionIf the tension `T` needed to hold the cart equilibrium is `(sqrt3W)/(x)` there is no friction. Find value of x
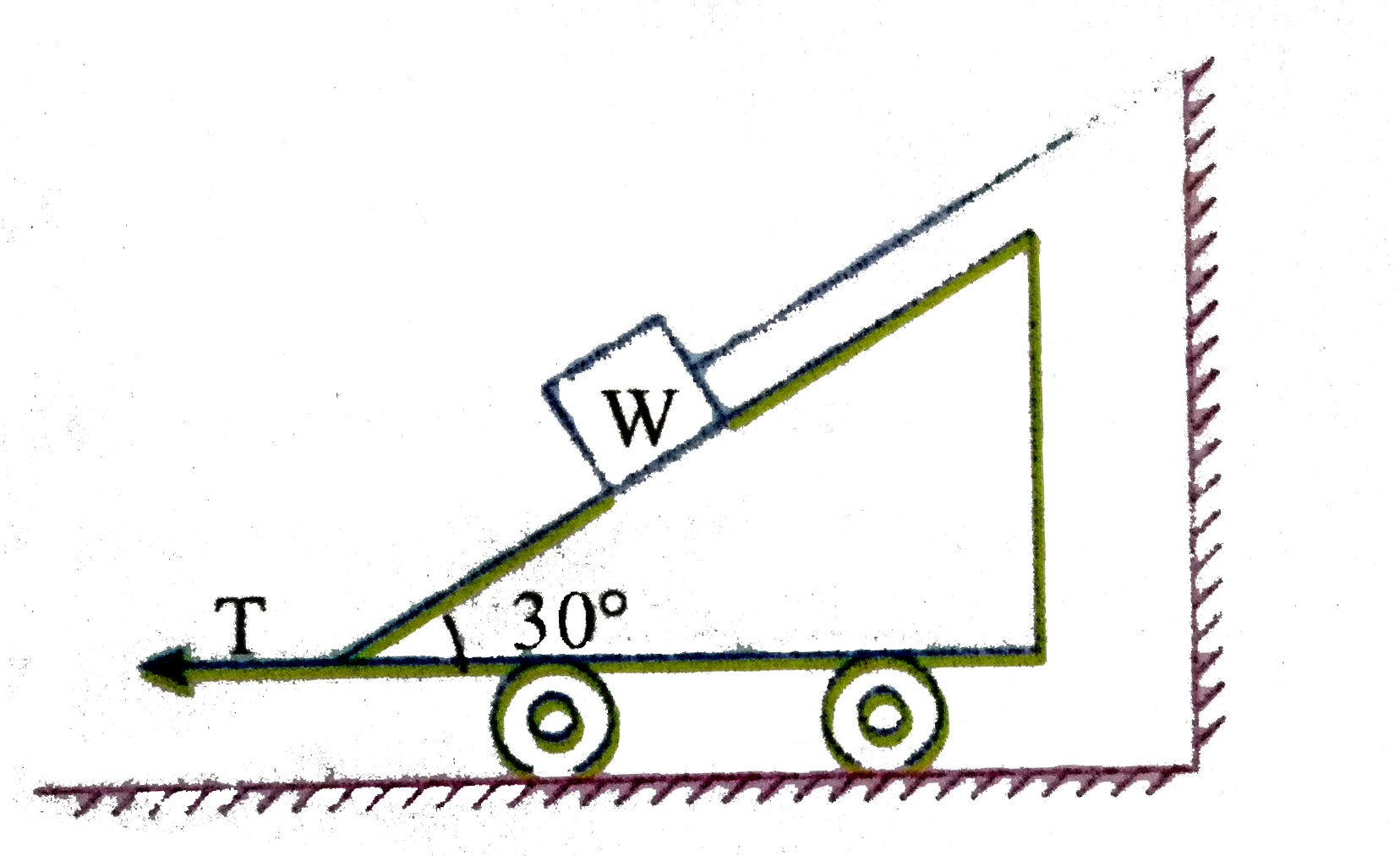 .
.
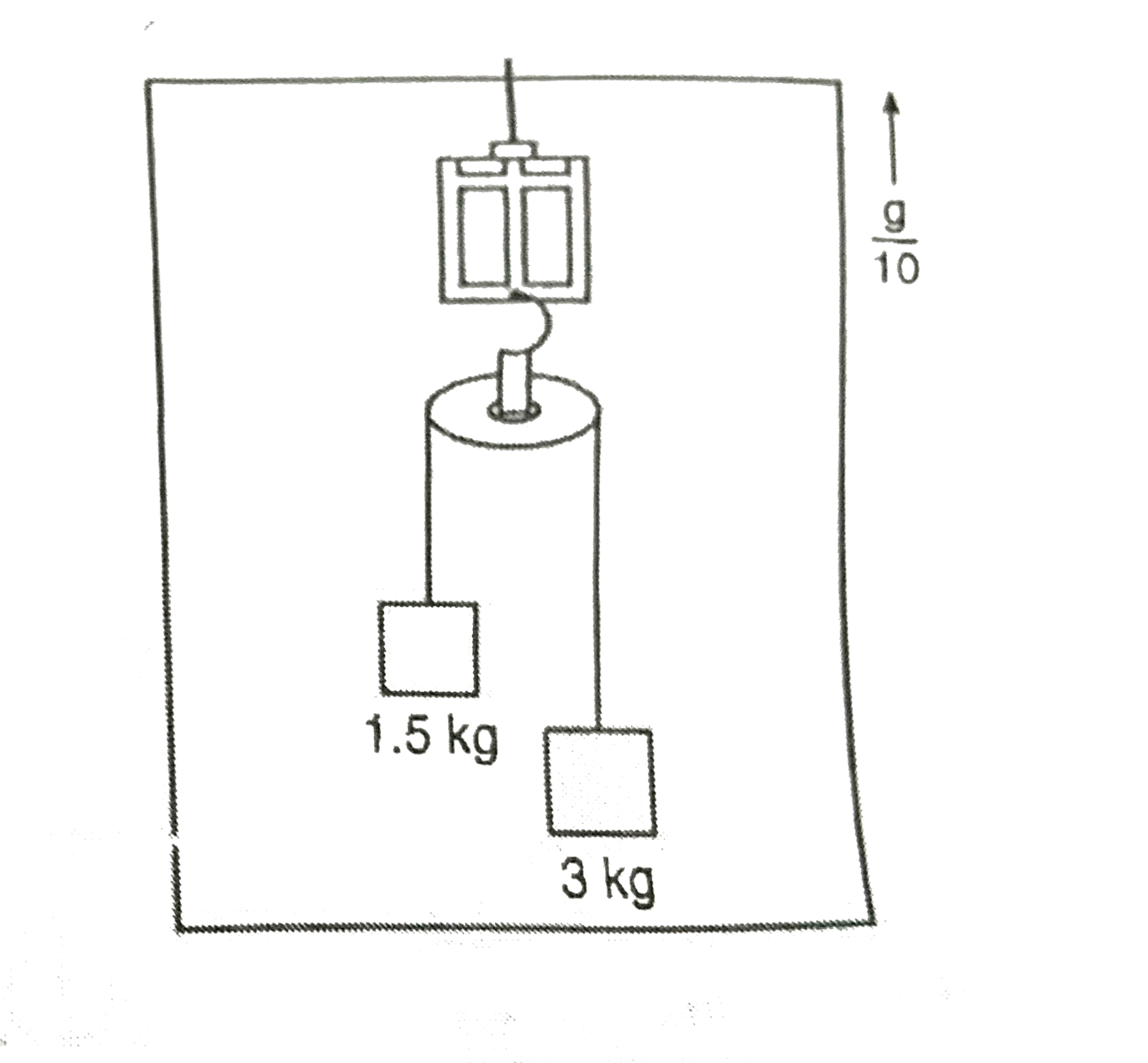
View SolutionThe elevator is going up with an acceleration of `g//10` the pulley and the string are light and the pulley is smooth. If reading of spring balance shown is `1.1x` Calculate x. (Take `g=10m//s^(2))`
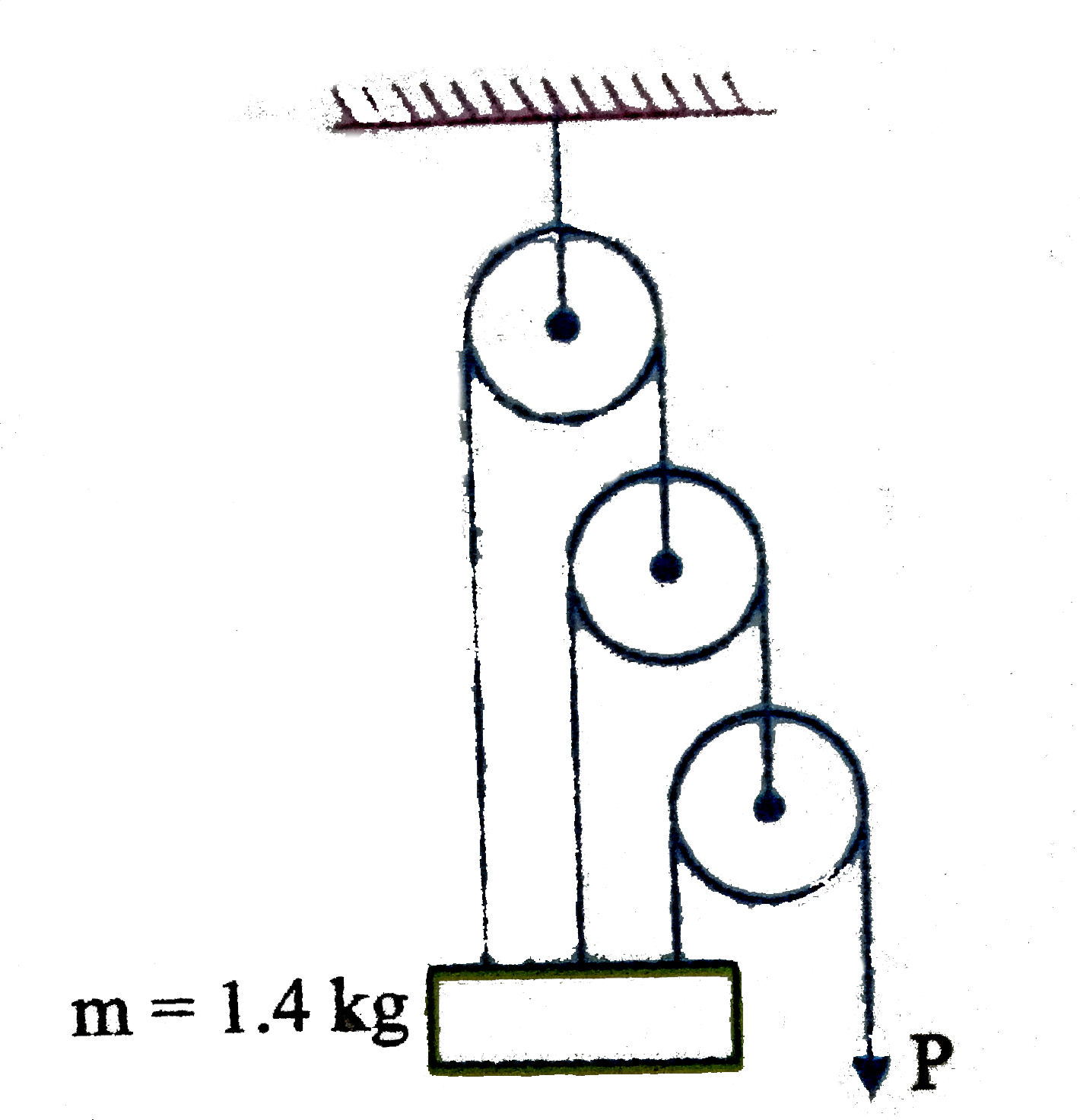
View SolutionThe pull `P` is just suffiient to keep the `14 N` block in equilibrium as shown Pulleys are ideal Find the tension (in N) in the cable connected with ceiling
 .
.
View SolutionIn the given find the and acceleration of `B` if instantaneous velocity and acceleration of `A` are as shown in the
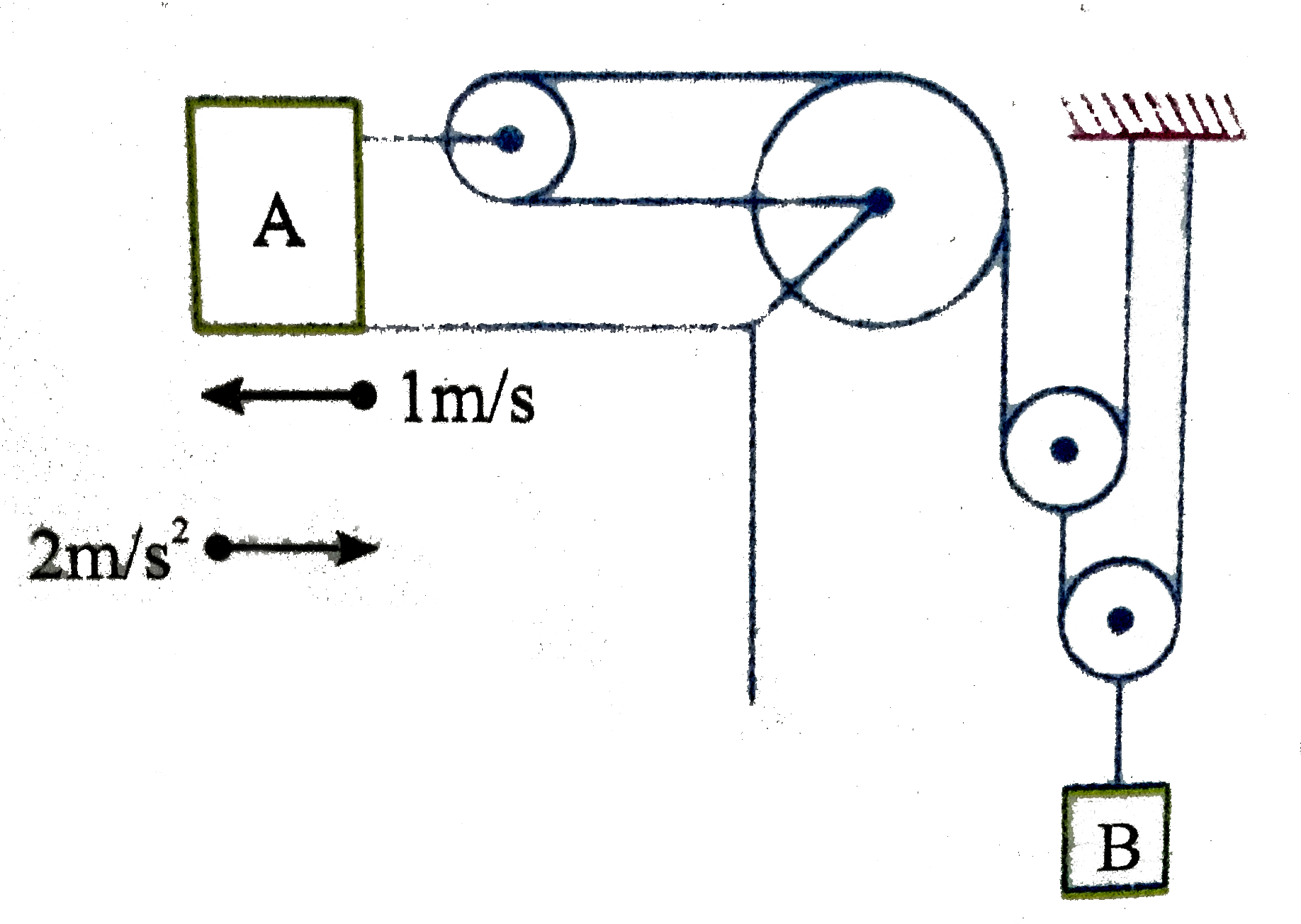 .
.
View Solutionshown, both blocks are released room rest. Length of `4kg` block is `2m` and of `1kg` is `4m`. Find the time they take to cross each other Assume pulley to be light and string to be light and inelastic
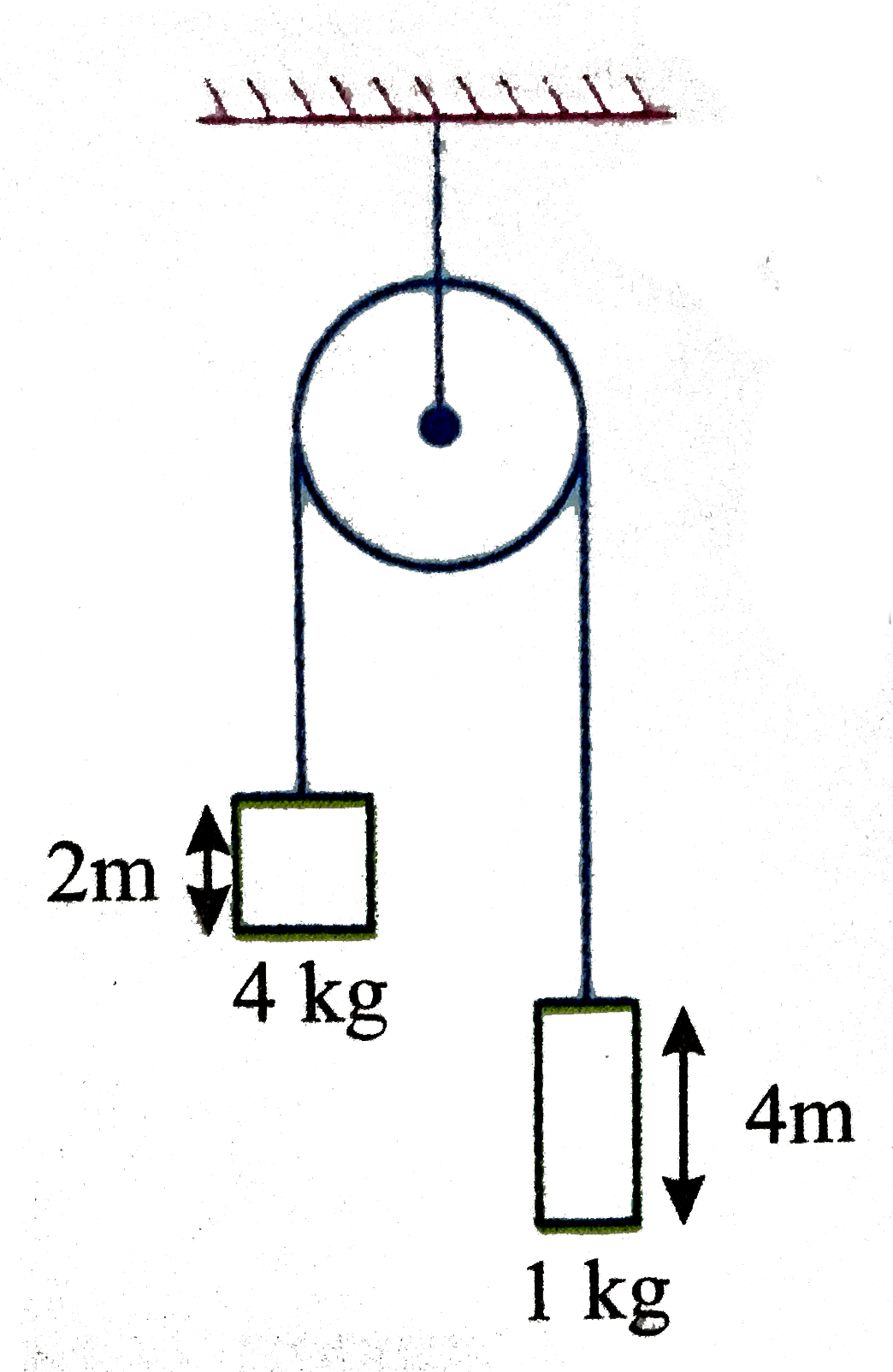 .
.
View SolutionTwo smooth blocks of same mass are connected by an inextensible and massless string which is passing over a smooth pulley are kept in a lift is going down with
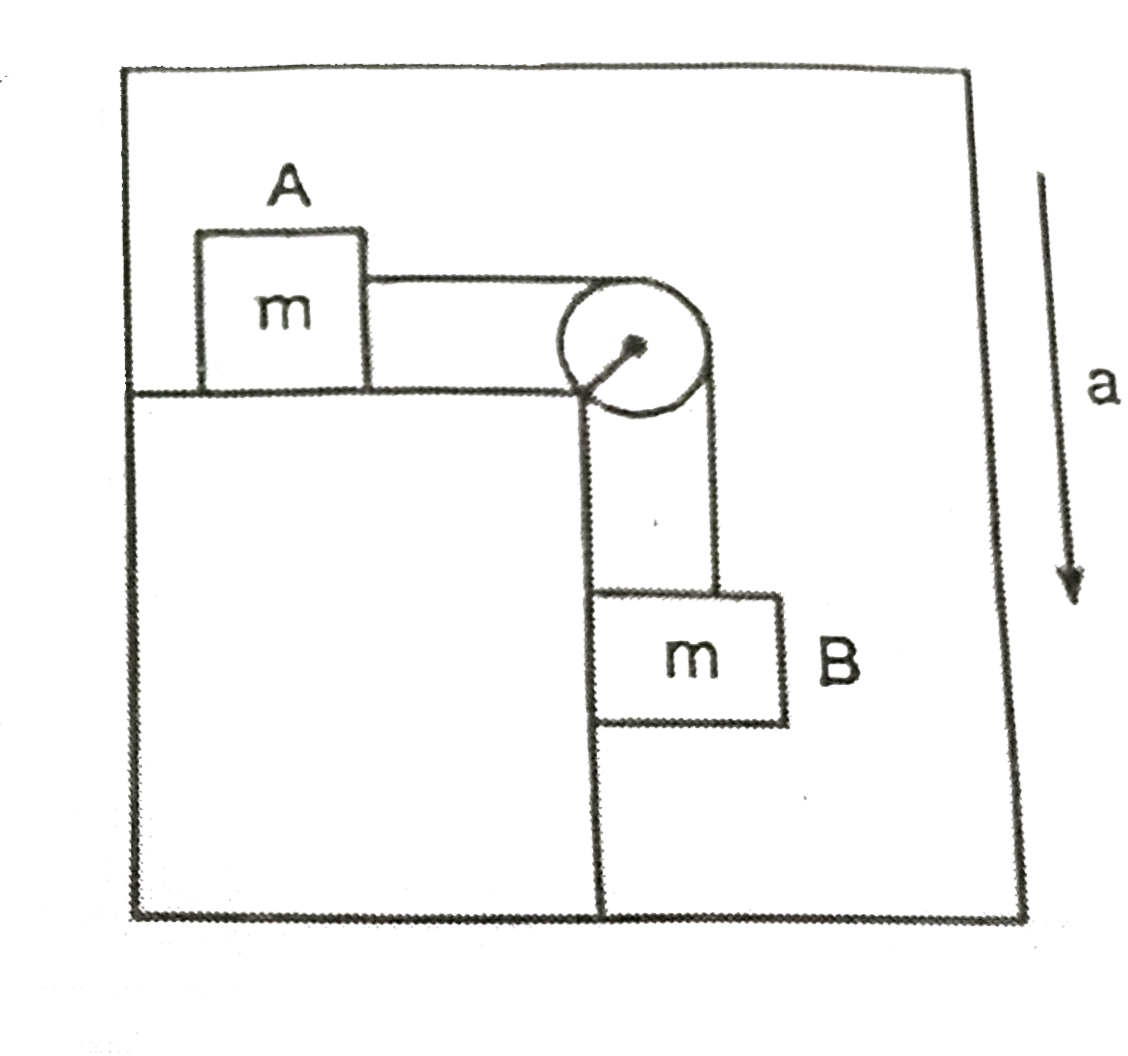
acceleration 'a' as shown in the fig What should be the value of a (in `m//s^(2))` so that acceleration of block A w.r.t. ground will be minimum? `(g=10m//s^(2))`
View SolutionFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration `10ms^(-2)`
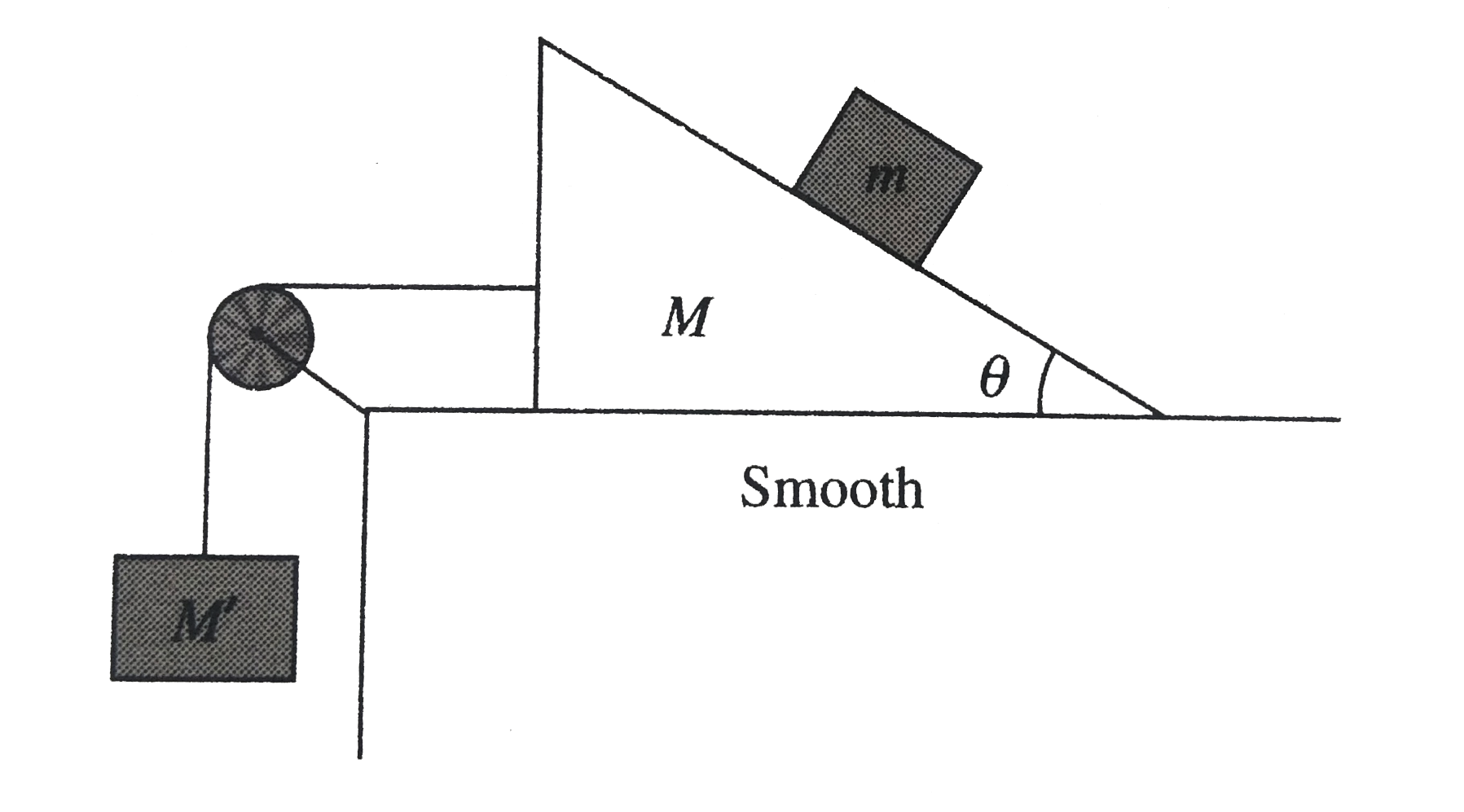
View SolutionThe masses of `10kig` and `20kg` respectively are connected by a massless spring as shown in figure. A force of `200N` acts on the `20kg` mass. At the instant shown, the `10kg` mass has acceleration `12m//sec^(2)` . What is the acceleration of `20kg` mass?

View SolutionTwo blocks A and B having masses `m_(1)=1 kg m_(2)=4 kg` are arranged as shown in the figure The pulleys P and Q are light and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that strings remains just taut. At moment t=0 a force F=30 t (N) starts acting on the pulley P along vertically upward direction as shown in the figure The time when the blocks A and B loose contact with ground is `4//x` sec then x is:
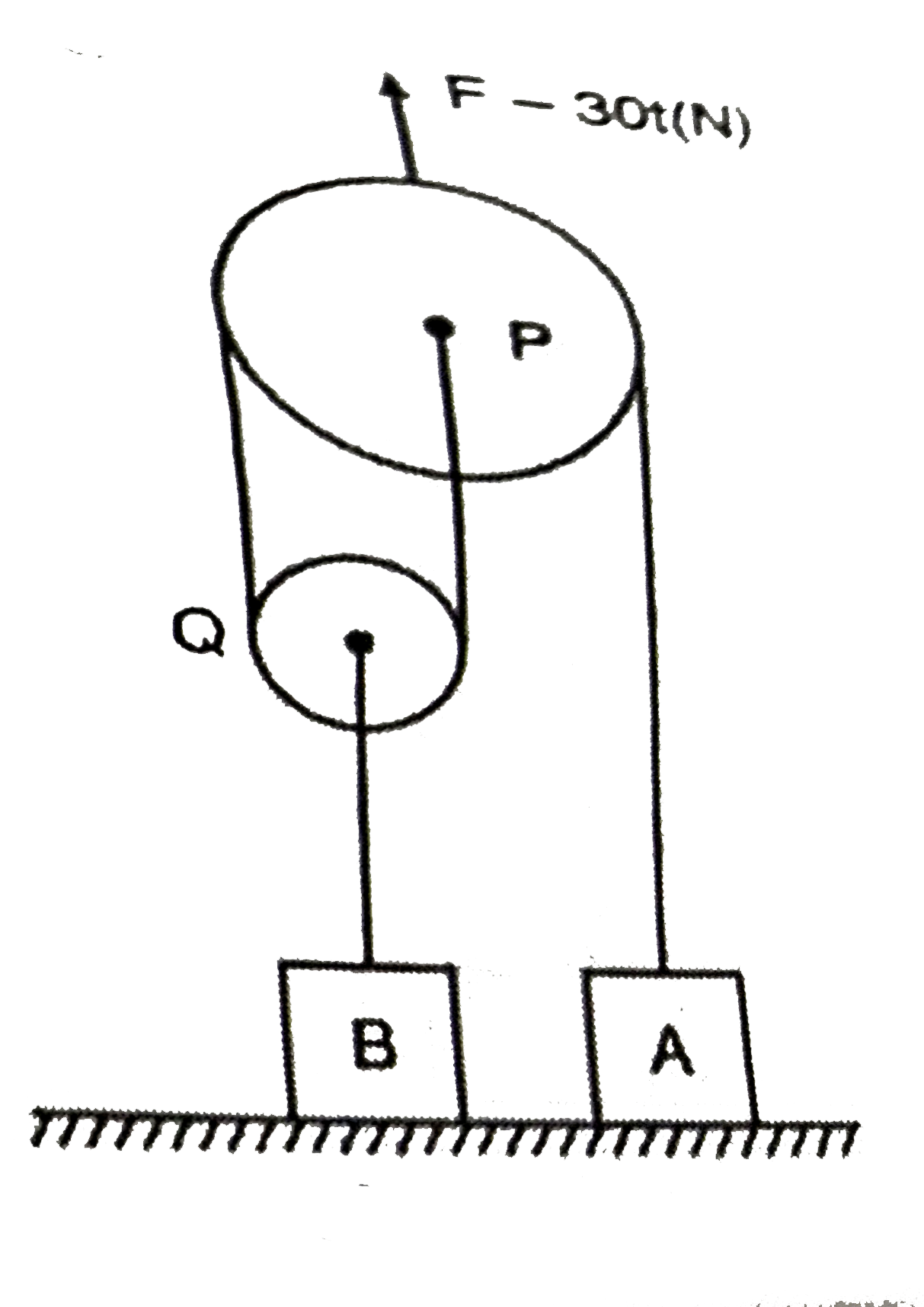
View SolutionIn the fig shown below, friction force between the bead and the light string is `(mg)/4` if `t=sqrt((nl)/(7g))` where t is the time in which the bead loose contact with the string after the system is released from rest, find n

View SolutionA bead `C` can move freely on a horizontal rod. The bead is connected by blocks `B` and `D` by a string as shown in the figure. If the velcoity of `B` is `v` The velcoity of block `D` is `4v//x` find the value of x
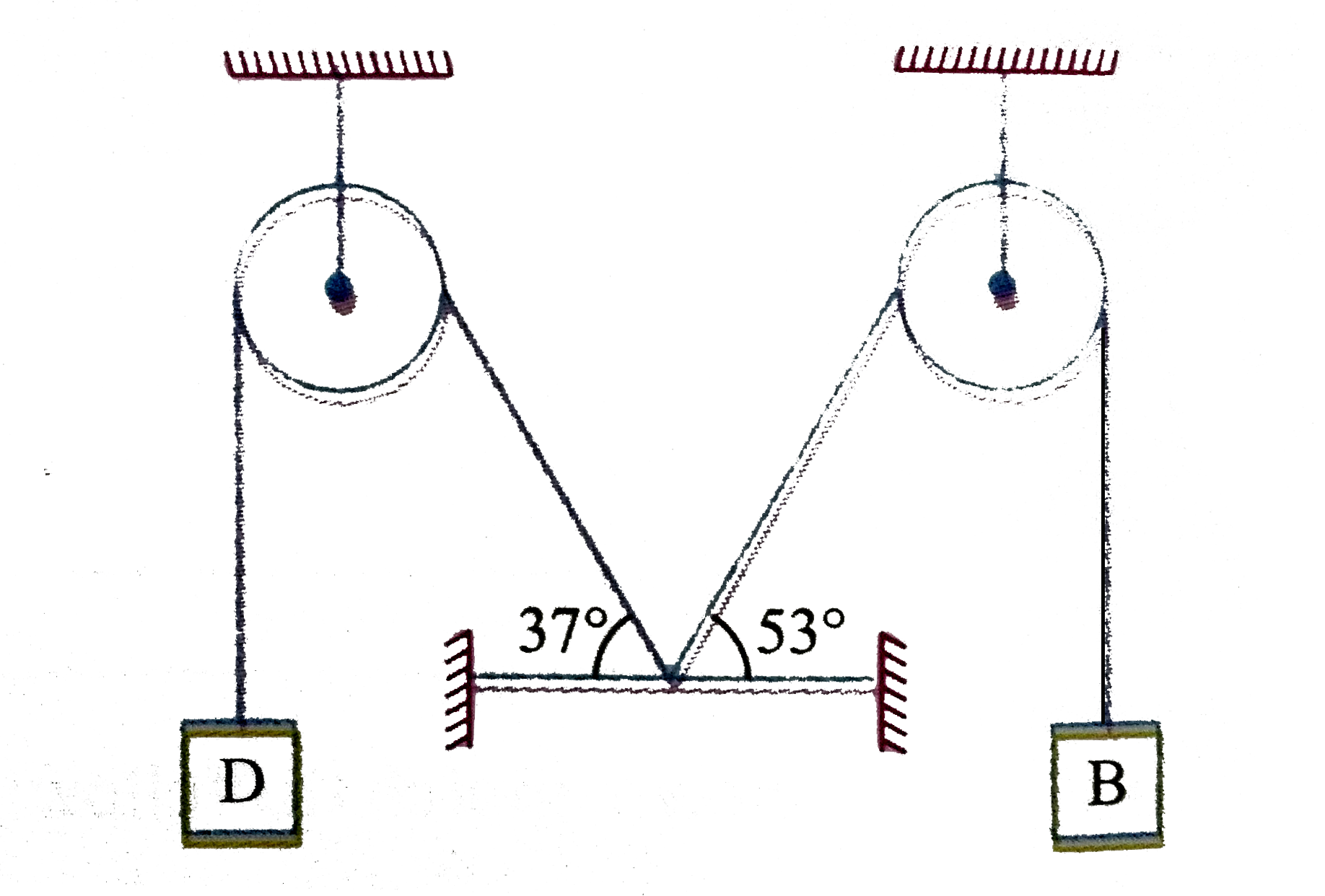 .
.
View SolutionA lift goes up with 10 m/s. a pulley P is fixed to the ceiling of the lift. To this pulley other two pulley `P_(1)` and `P_(2)` are attached. `P_(1)` moves up with velocity 30 m/s. A moves up with velocity 10 m/s. D is moving downwards with velocity 10 m/s at same instant of time. Find the velocity of B and that of C at that instant. Assume that all velocities are relative to the ground.

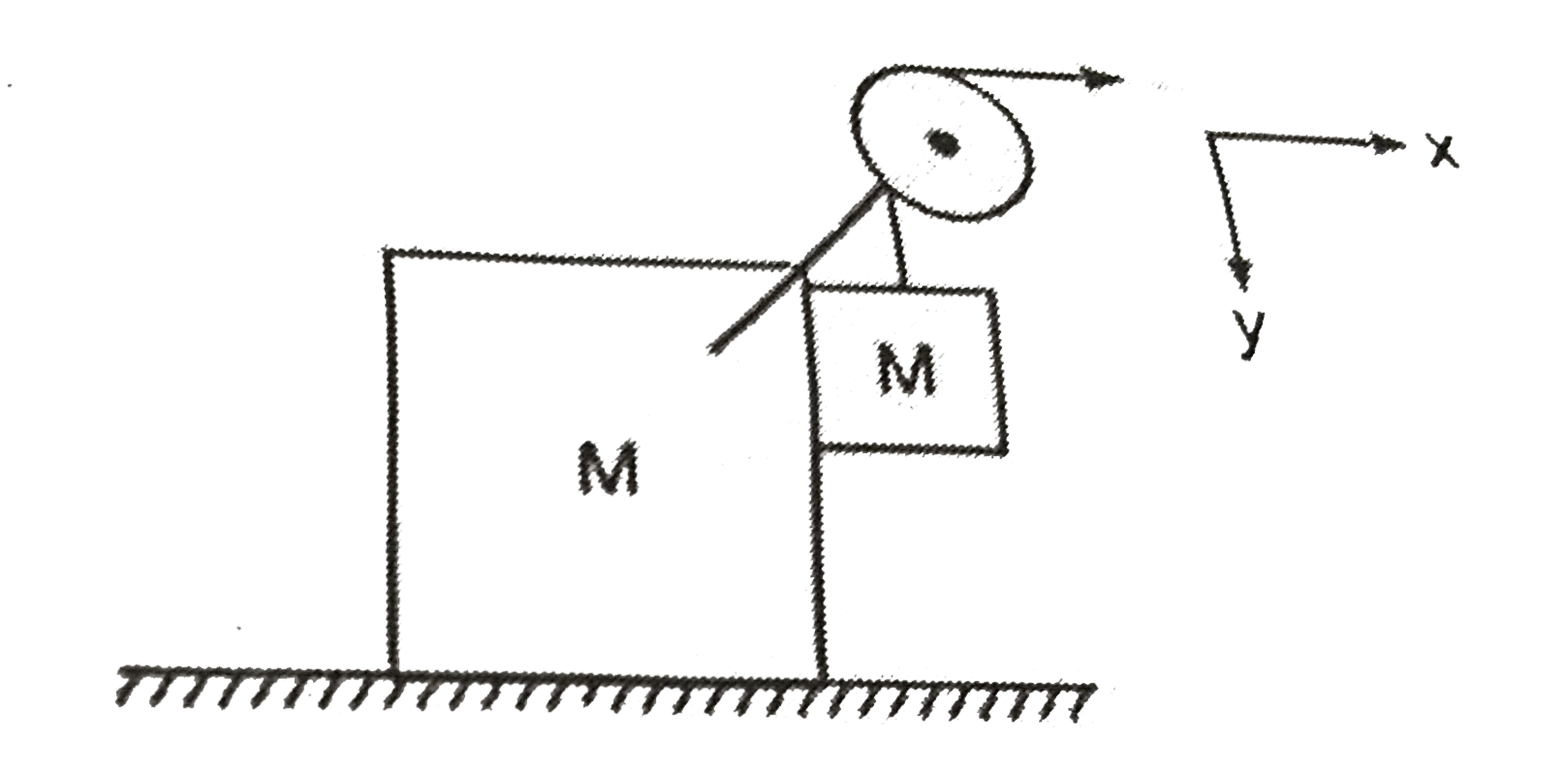
View SolutionIn the situation given, all surfaces are frictionless. Pulley is ideal and string is light if `F=mg//2` the acceleration of the big block is `g//x` then x is:
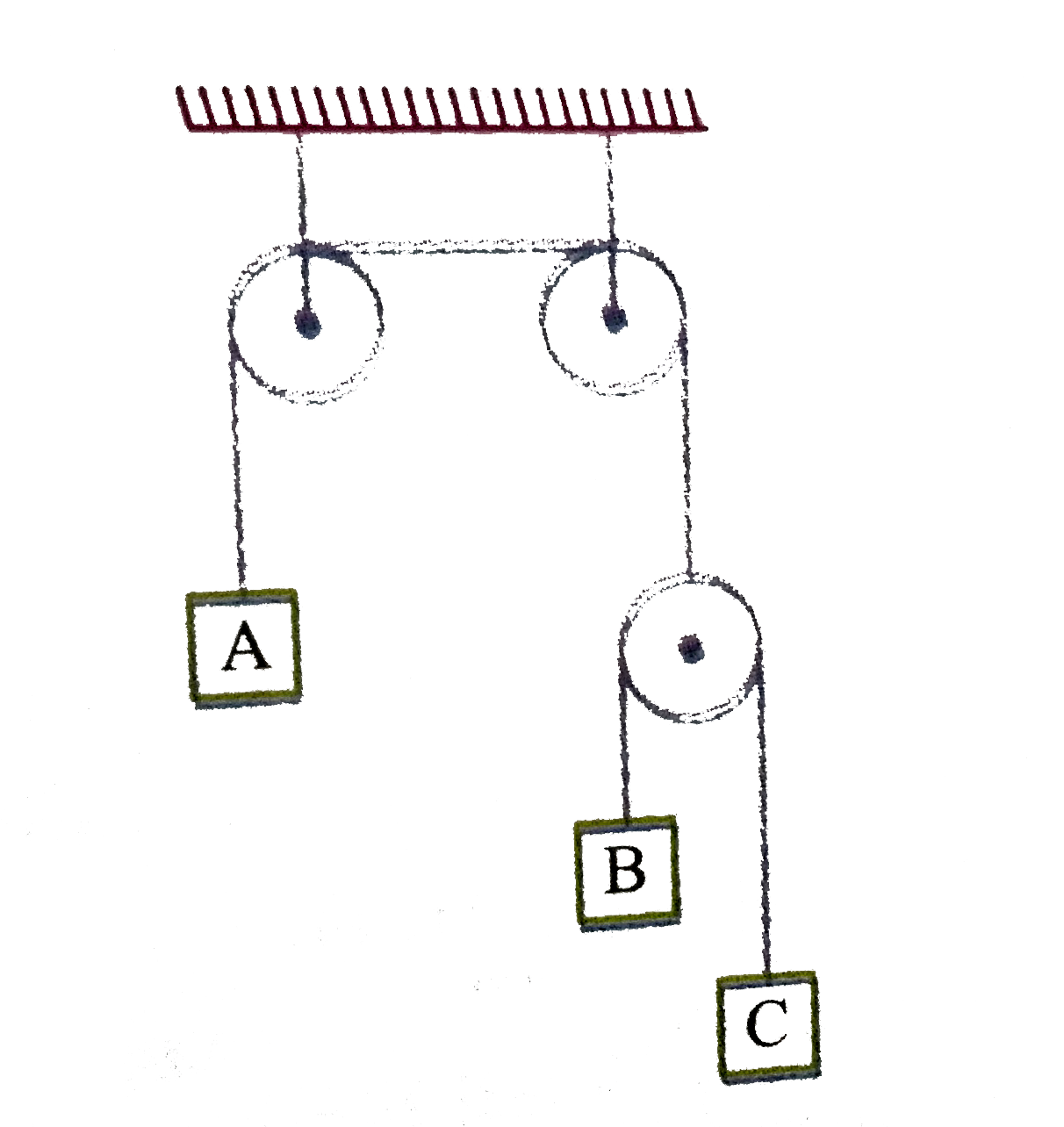
View SolutionThree blocks shown in move vertically with constant velocities The relative velocity of w.r.t `C` is `100m//s` upward and the relative velocity of `B` w.r.t A is `50m//s` downward. All the string are ideal The velocity of `C` with respect to ground is `125//x` calculate x
 .
.
View SolutionBlock A of mass m is placed over a wedge of same mass m. Both the block and wedge are placed on a fixed inclined plane. Assuming all surfaces to be smooth, the displacement of the block A in ground frame in 1s is `(gsin^(2)theta)/(x+sin^(2)theta)` then the value of x is:
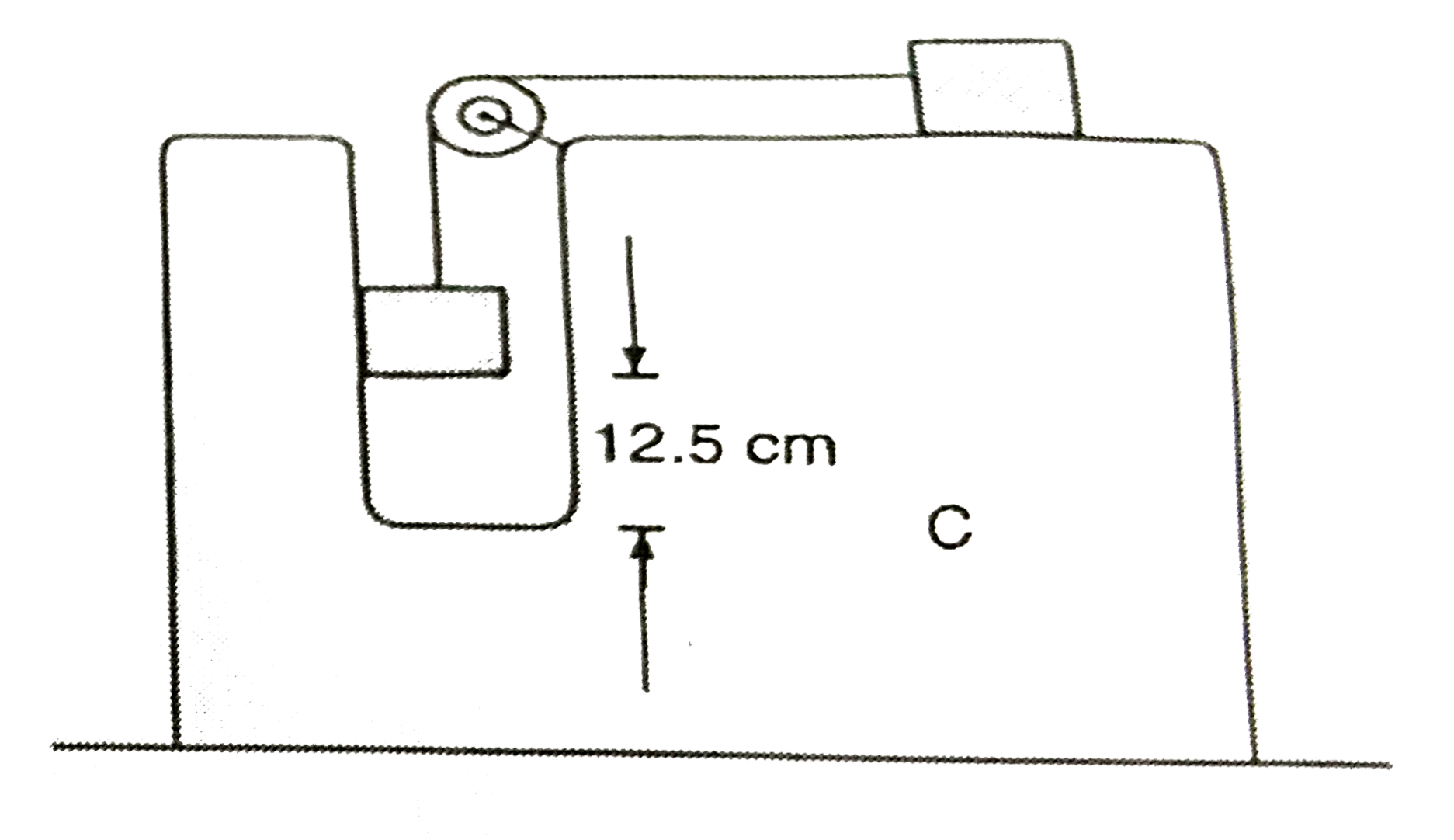
View SolutionA small, light pulley is attached with a block C of mass 4 kg as shown in fig A block B of mass `1.5kg` is placed on the top horizontal surface of C. Another block A of mass 2 kg is hanging from a string, attached with B and passing over the pulley. Taking `g=10 ms^(-2)` and neglecting friction, acceleration of block C when the system is released from rest is `x//4` calculate x.
View SolutionA system is shown in the End `B` of string is moving upwards with `sqrt3 m//s` Pulley is moving with speed `2 sqrt3 m//s` in direction shown in the figure. The velocity of the block A is `x + 2sqrt3 (m//s)` find x
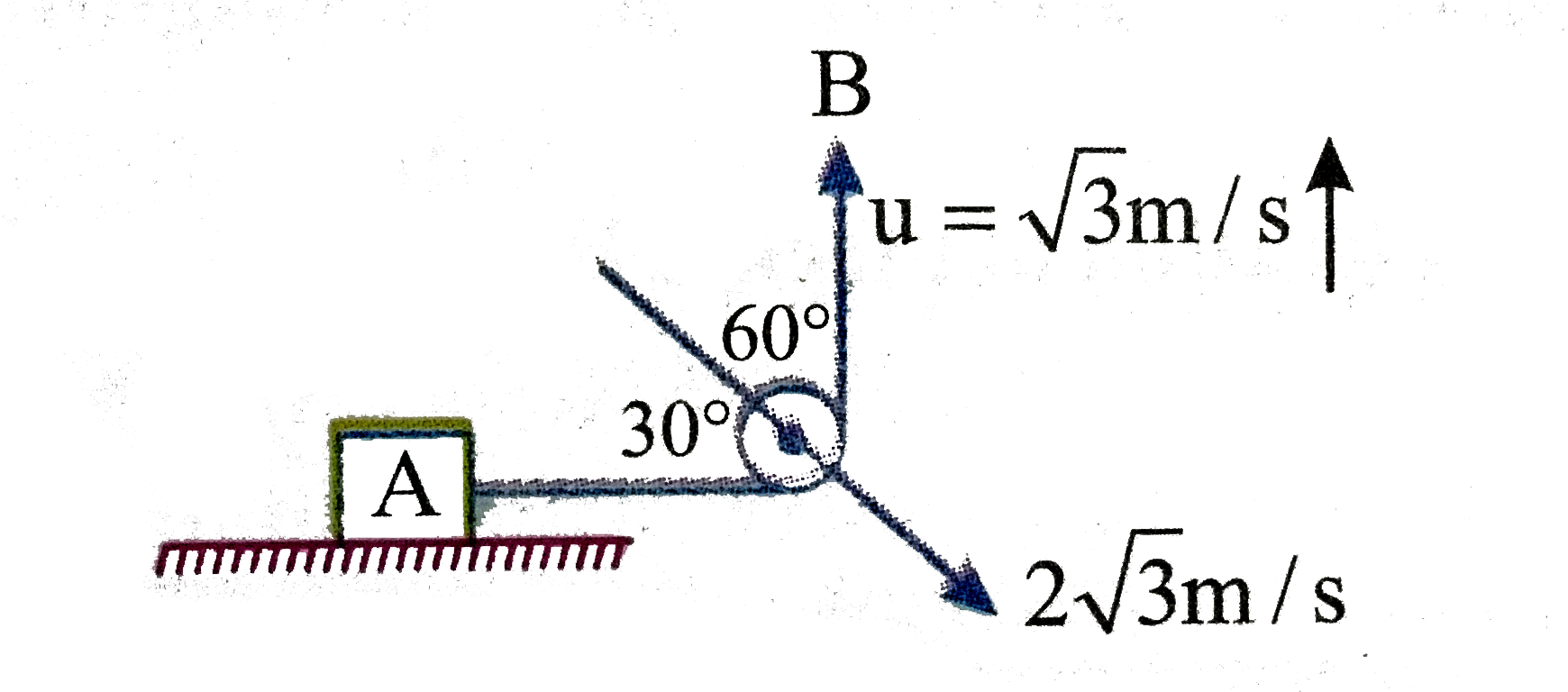 .
.
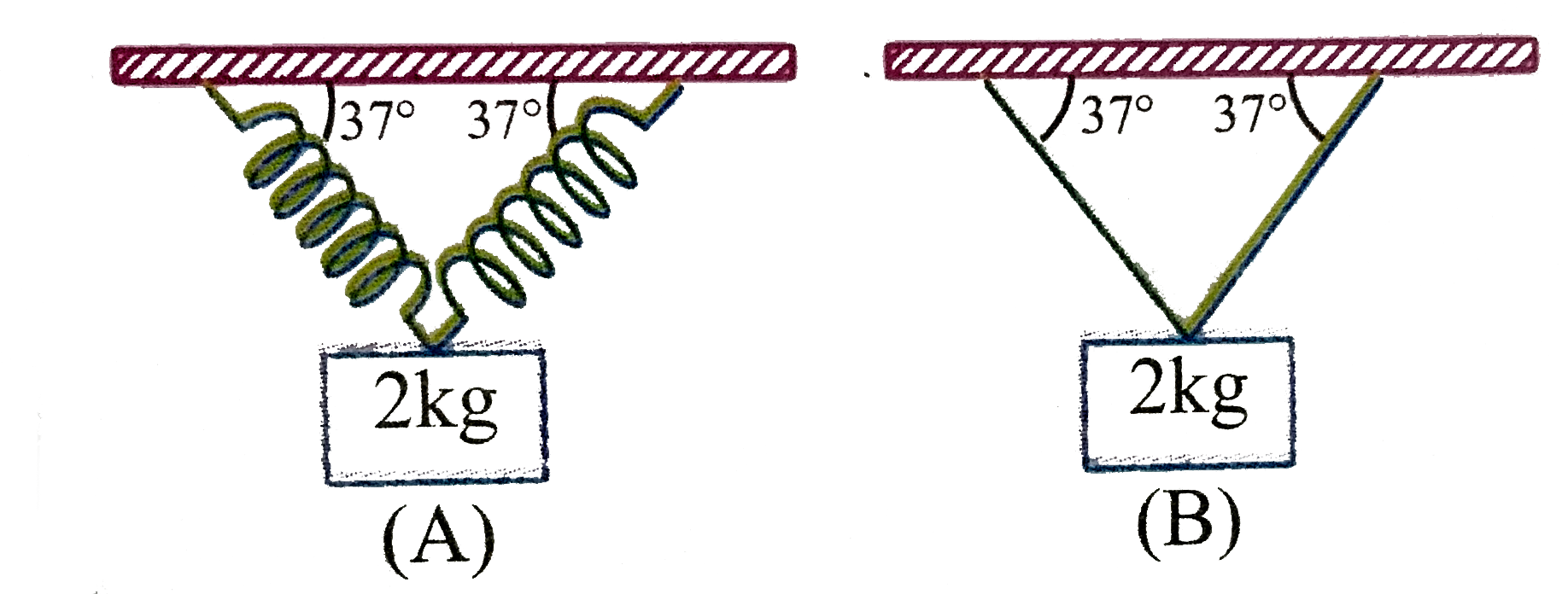
View SolutionIf at `t =0` right spring in (A) and right string in (B) breaks The ratio of magnitudes of instantaneous acceleration of blocks `A` & `B` is ` (5x)/(24)` calculate x
 .
.
View SolutionIn the shown `P_(1)` and `P_(2)` are massless pulleys `P_(1)` is fixed and `P_(2)` can move Masses of `A,B` and `C` are `(9m)/(64) 2m` amd m respectively All contacts are smooth and the string is massless `theta = tan^(-1)((3)/(4))` (Take `g = 10m//s^(2)`)
The tension in string connecting pulley `P_(2)` and block `C` is `(13)/(x)` Calculate x (Take `m =1 kg`)
 .
.
View SolutionIn the arrangement shown in the figure, pulleys are light, small and smooth. Mass of blocks `A,B` and `C` is `m_(1) =14 kg, m_ (2) =11kg` and `M =52kg` respectively. The block A can slide freely along a vertical rail fixed to left vertical face of block `C` Assuming all the surface to be smooth magntitude of acceleration of block A is `sqrt((10)/(A)` Calculate x
 .
.
View Solution
INTEGER TYPE QUESTIONS questions and complete solutions for chapter NEWTONS LAWS OF MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11