Complete Solutions to Solved Example of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| NARAYANA | Solved Example |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
A force produces an acceleration `16m^(-2)` in a mass `0.5 kg` and an acceleration `4ms^(-2)` in an unknown mass when appied separately If both the masses are tied together what will be the acceleration under same force ? .
View SolutionWhen forces `F_(1)` , `F_(2)` , `F_(3)` are acting on a particle of mass m such that `F_(2)` and `F_(3)` are mutually prependicular, then the particle remains stationary. If the force `F_(1)` is now rejmoved then the acceleration of the particle is
View SolutionA body of mass `m = 3.513 kg` is moving along the x-axis with a speed of `5.00ms^(-1)`. The magnetude of its momentum is recorded as
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
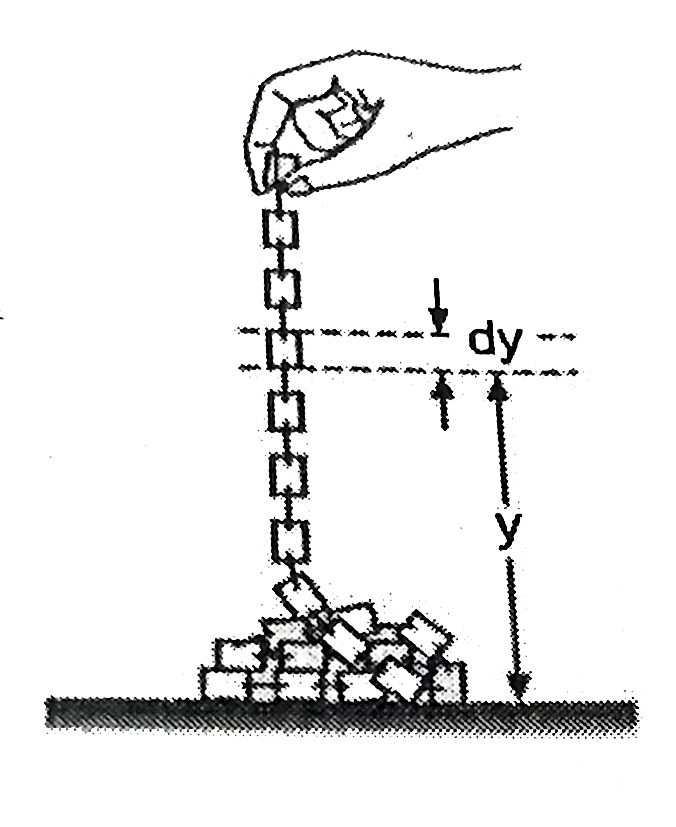
View SolutionA body of mass `8kg` is moved by a force `F = (3x)N`, where x is the disatance covered Initial position is `x =2m` and final position is `x =10m` If initially the body is at rest find the final speed .
View SolutionSum of magnitudes of the two forces acting at a point is `16 N` if their resultant is normal to the smaller forces and has a magnitude `8N` then the forces are .
View SolutionA particle is at rest at `x=a`. A force `vecF=(b)/(x^(2))veci`
begins to act on the particle. The particle starts its motion, towards the origin, along X-axis. Find the velocity of the particle, when it reaches a distance x from the origin .
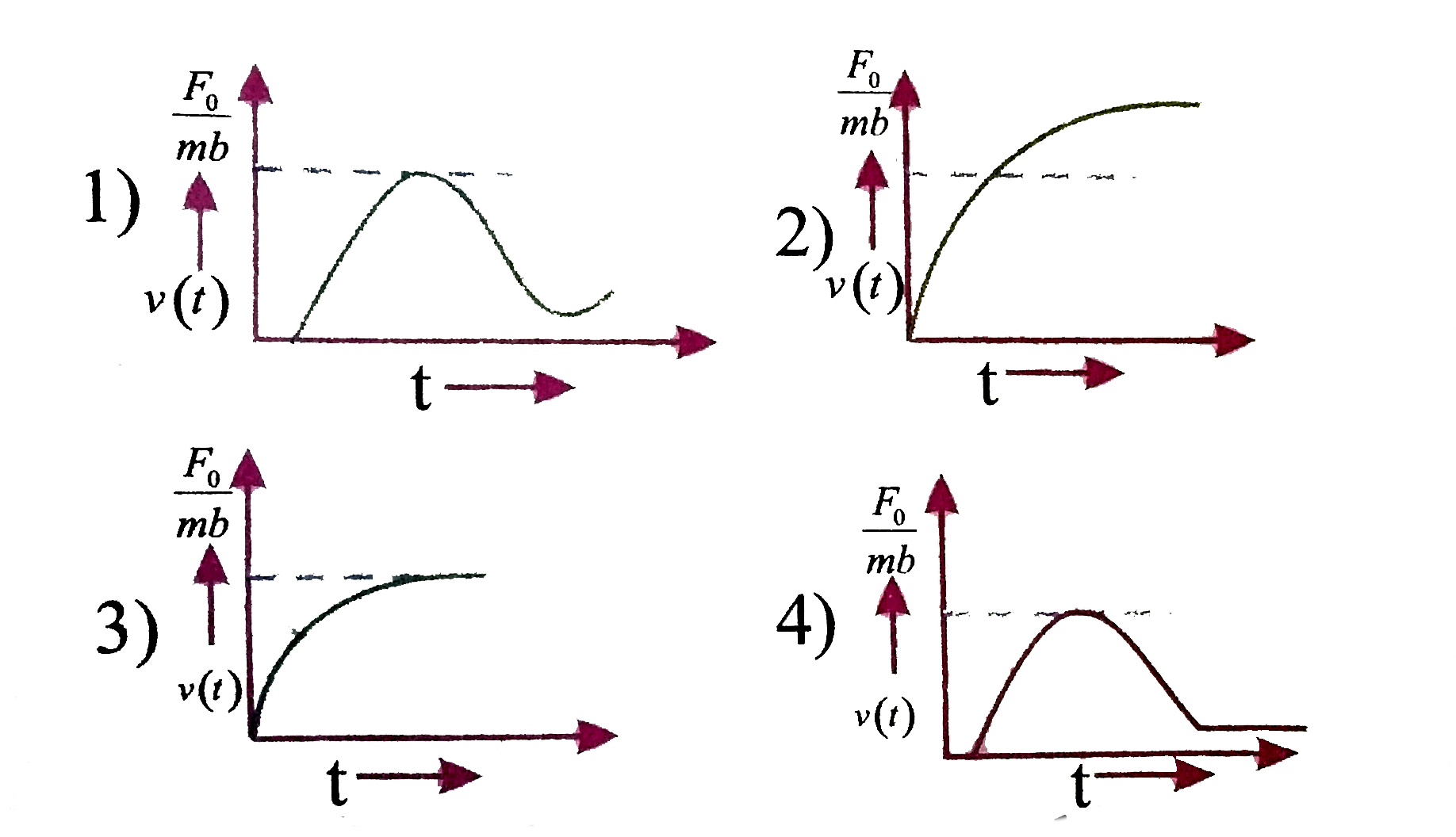
View SolutionA particle of mass m is at rest at the origin at time `t=0` It is subjected to a force `F(t)=F_(0)e^(-bt)` in the X-direction. Its speed `V(t)` is depicted by which of the following curves
View SolutionA bus moving on a level road with a velocity v can be stopped at a distance of x by the application of a retarding force `F` The load on the bus is increased by `25%` by boarding the passengers. Now if the bus is moving with the same speed and if the same retarding force is applied the distance travelled by the bus before it stops is .
View SolutionA gardener is watering plants at the rate `0.litre//sec` using a pipe of cross-sectional area `1cm^(2)` What additional force he has to exert if he desires to increase the rate of watering two times ? .
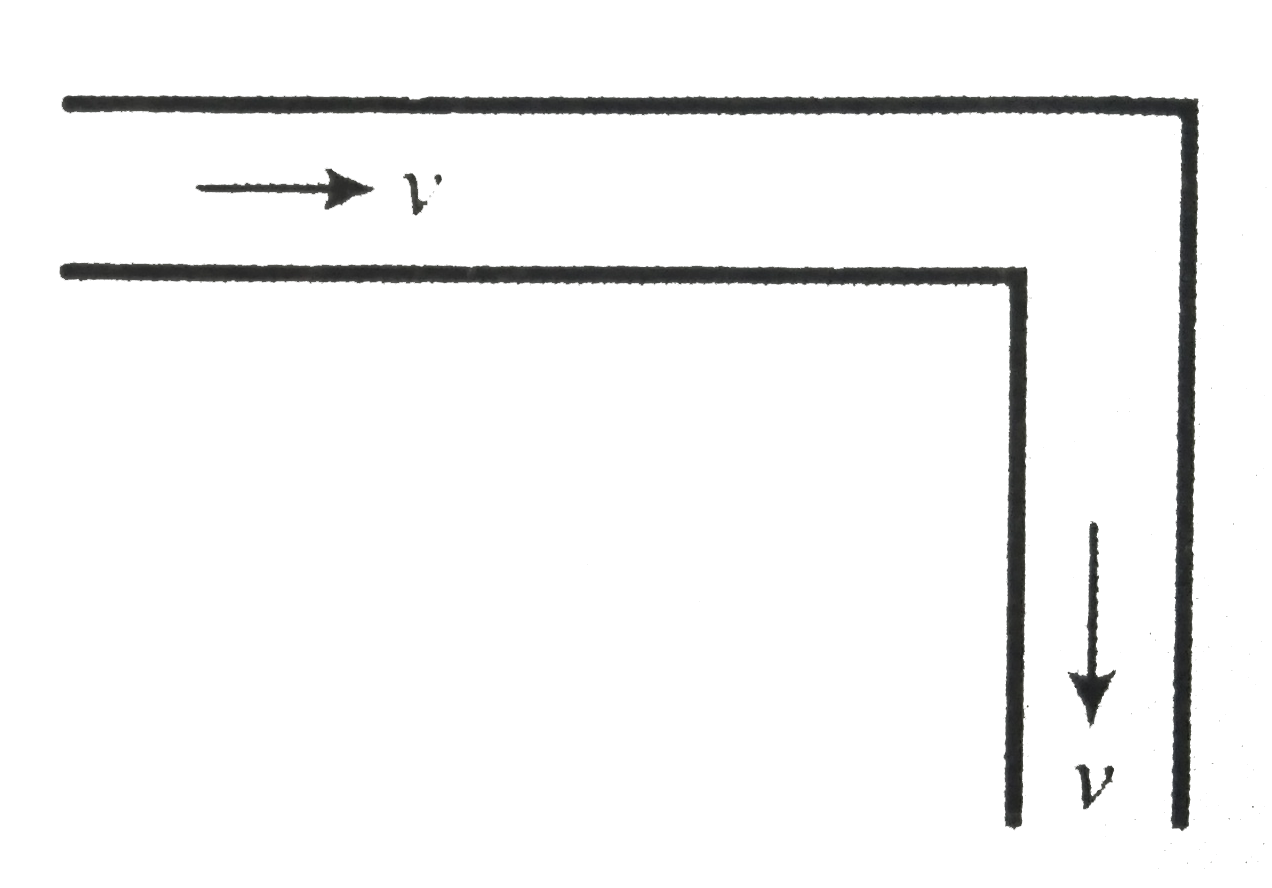
View SolutionA liquid of density `rho` is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
View SolutionA plate moves normally with the speed `v_(1)` towads a horizontal jet of uniform area of cross-section. The jet discharge water at the rate of volume `V` per second at a speed of `v_(2)`. The density of water is `rho`. Assume that water splashes along the surface of the plate ar right angles to the original motion. The magnitude of the force action on the plate due to the jet of water is
View SolutionFind the impulse due to the force
`vecF=ahati+bthatj`,where `a =2N` and `b=4Ns^(-1)` if this force acts from `t_(i) =0` to `t_(f) =0.3s` .
View SolutionA ball falling with velocity `vecv_(i)=(-0.65hati-0.35hatj)ms^(-1)` is subjected to a net impulse `vecI=(0.6hati+0.18hatj)` Ns. If the ball has a mass of `0.275kg` calculate its velocity immediately following the impulse .
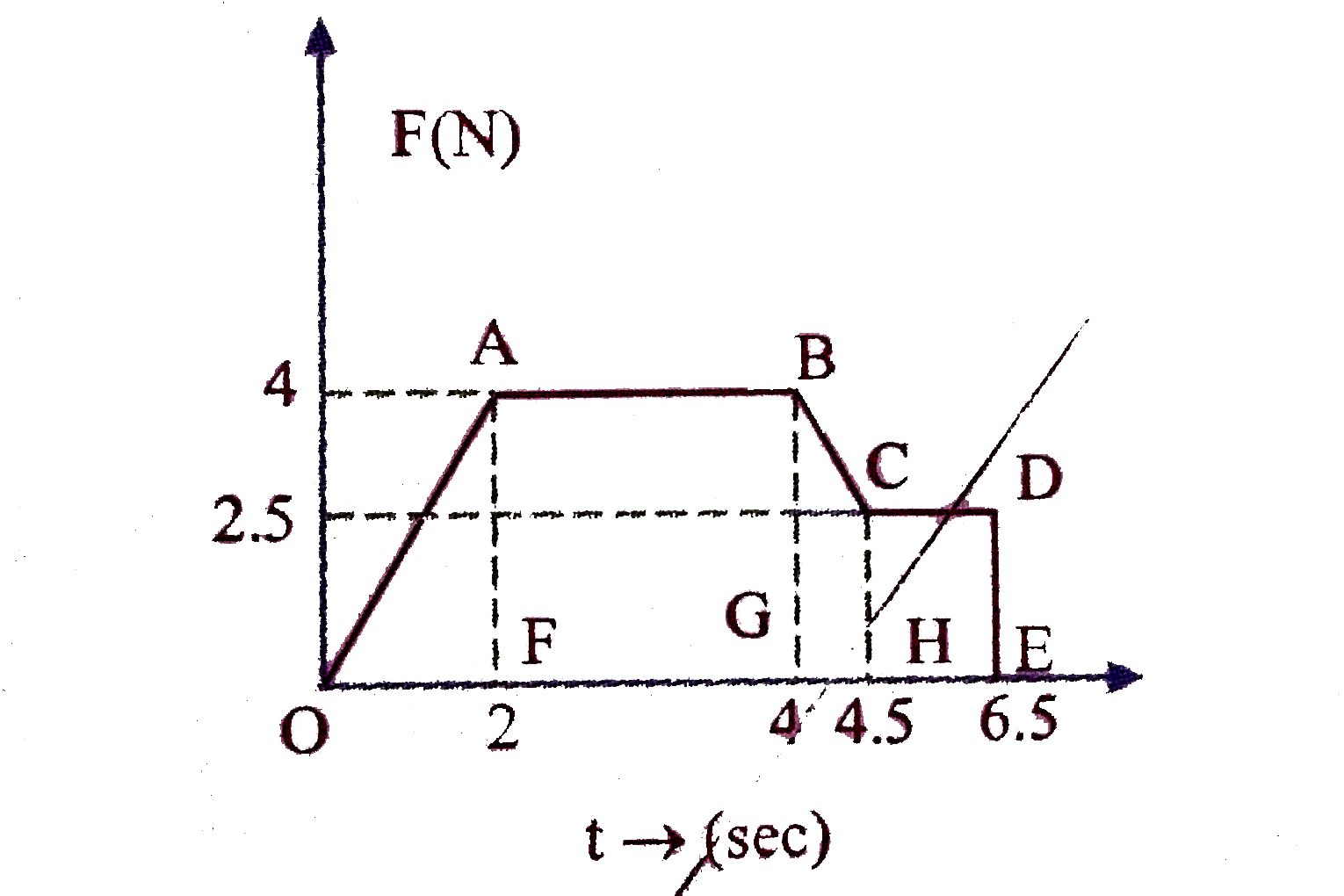
View SolutionA body of mas `2kg` has an initial speed `5ms^(-1)` A force acts on it for some time in the direction of motion The force-time graph is shown. Find the final speed of the body
 .
.
View SolutionA bullet is fired from a gun The force on a bullet is `F =600 -2 xx 10^(5) t` newton. The force reduces to zero just when the bullet leaves barrel Find the impulse imparted to the bullet .
View SolutionA mass of `3kg` is suspended by a rope of length `2m` from the ceilling A force of `40N` in the horizontal direction is applied atmidpoint `P` of the rope the as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, `g =10m//s^(2))` .
View SolutionA mass `M` is suspended by a weightless string The horizontal force required to hold the mass `60^(@)` with the vertical is .
View SolutionA chain of mass 'm' is attached at two points `A` and `B` of two fixed walls as shown in the Find the tension in the chain near the walls at point `A` and at the mid point `C`
 .
.
View SolutionA mass of `1kg` attached to one end of a string is first lifted up with an acceleration `4.9m//s^(2)` and then lowered with same acceleration What is the ratio of tension in string in two cases .
View SolutionThe apparent weight of a man in a lift is `W_(1)` when lift moves upwards with some acceleration and is `W_(2)` when it is accerating down with same acceleration. Find the true weight of the man and acceleration of lift .
View SolutionThree blocks connected together by strings are pulled along a horizontal surface by applying a force `F. If F =36N` What is the tension `T_(2)` ?.
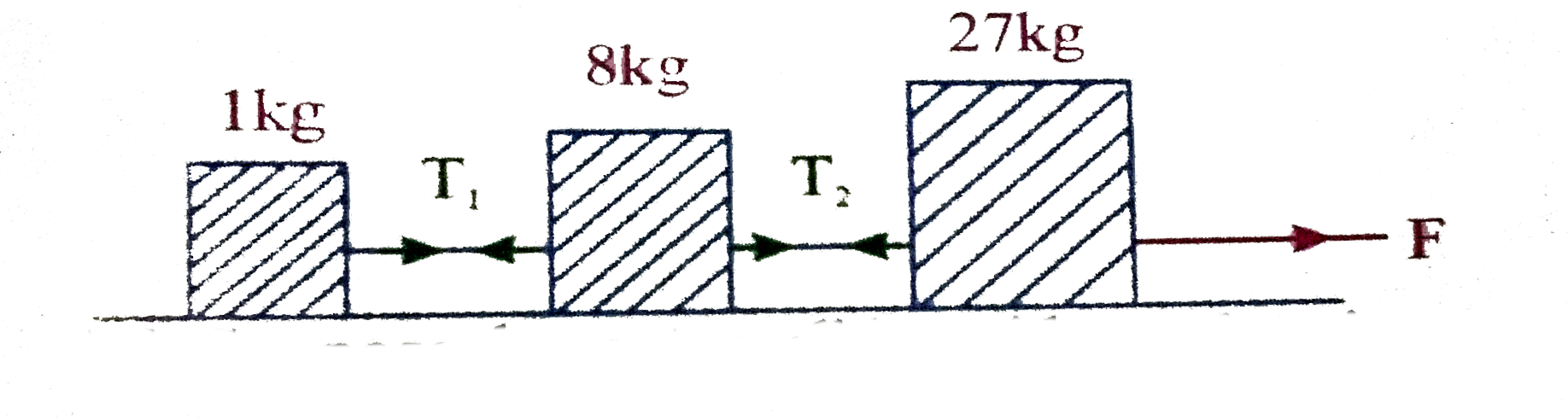 .
.
View SolutionThe maximum tension a rope can withstand is `60 kg-wt` The ratio of maximum accelertion with which two boys of masses `20kg` and `3kg` can climb up the rope at the same time is .
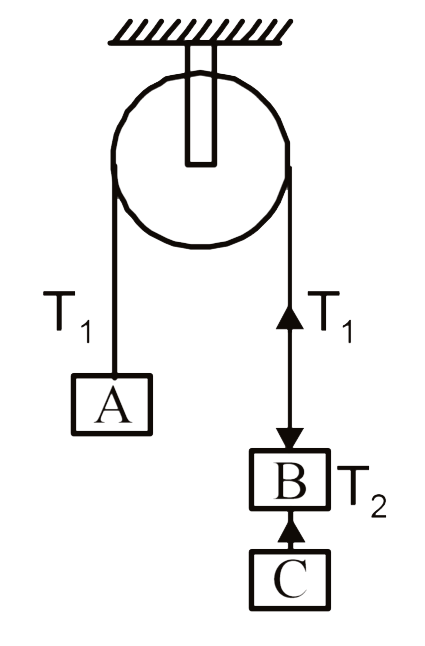
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in fig. The tensions in the string connecting weights A to B and B to C will respectively be -
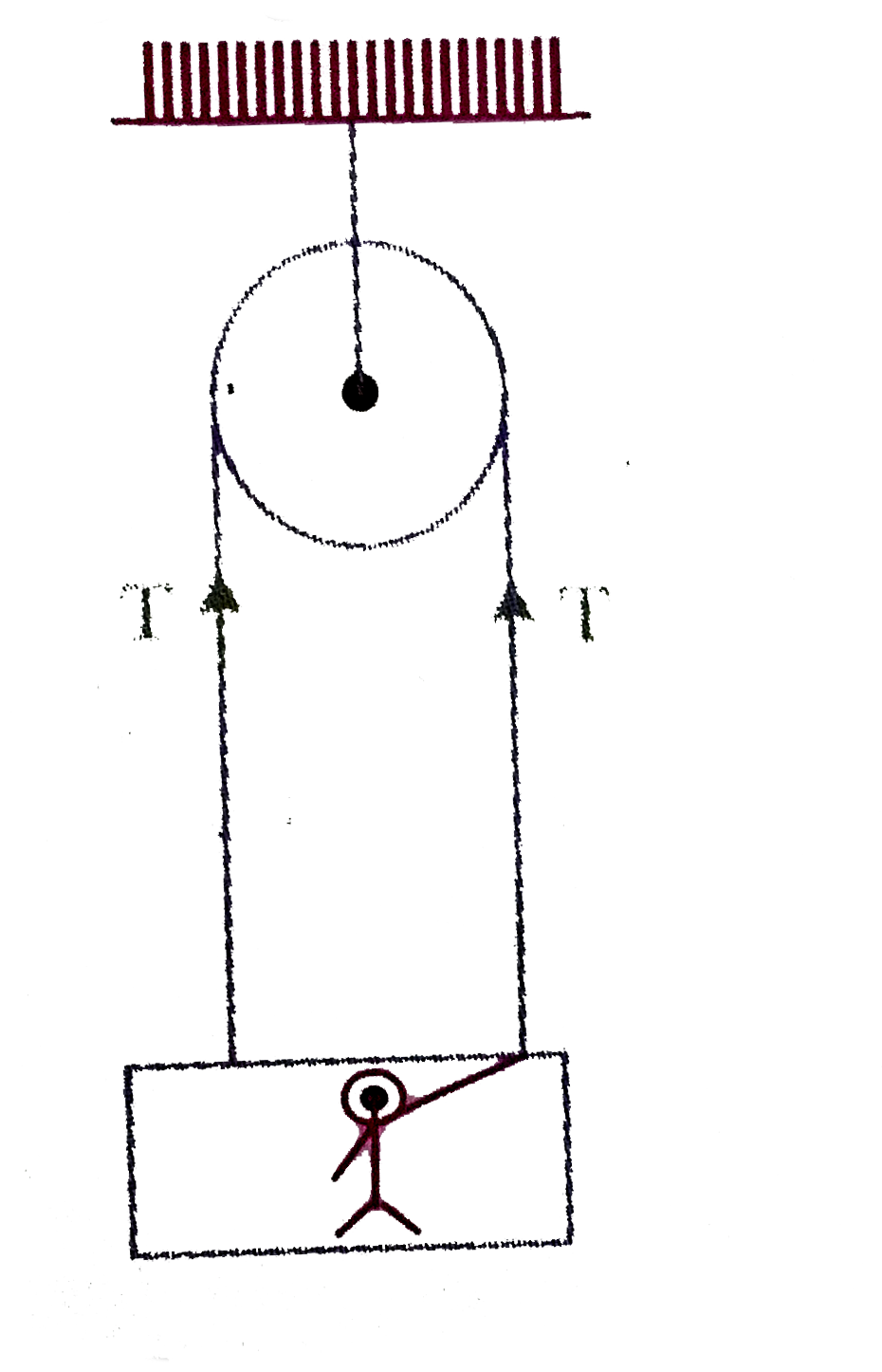
View SolutionA man of mass `60kg` is standing on a weighing machine kept in a box of mass `30kg` as shown in the diagram If the man man ages to keep the box stationary, find the read ing of the weighing machine
 .
.
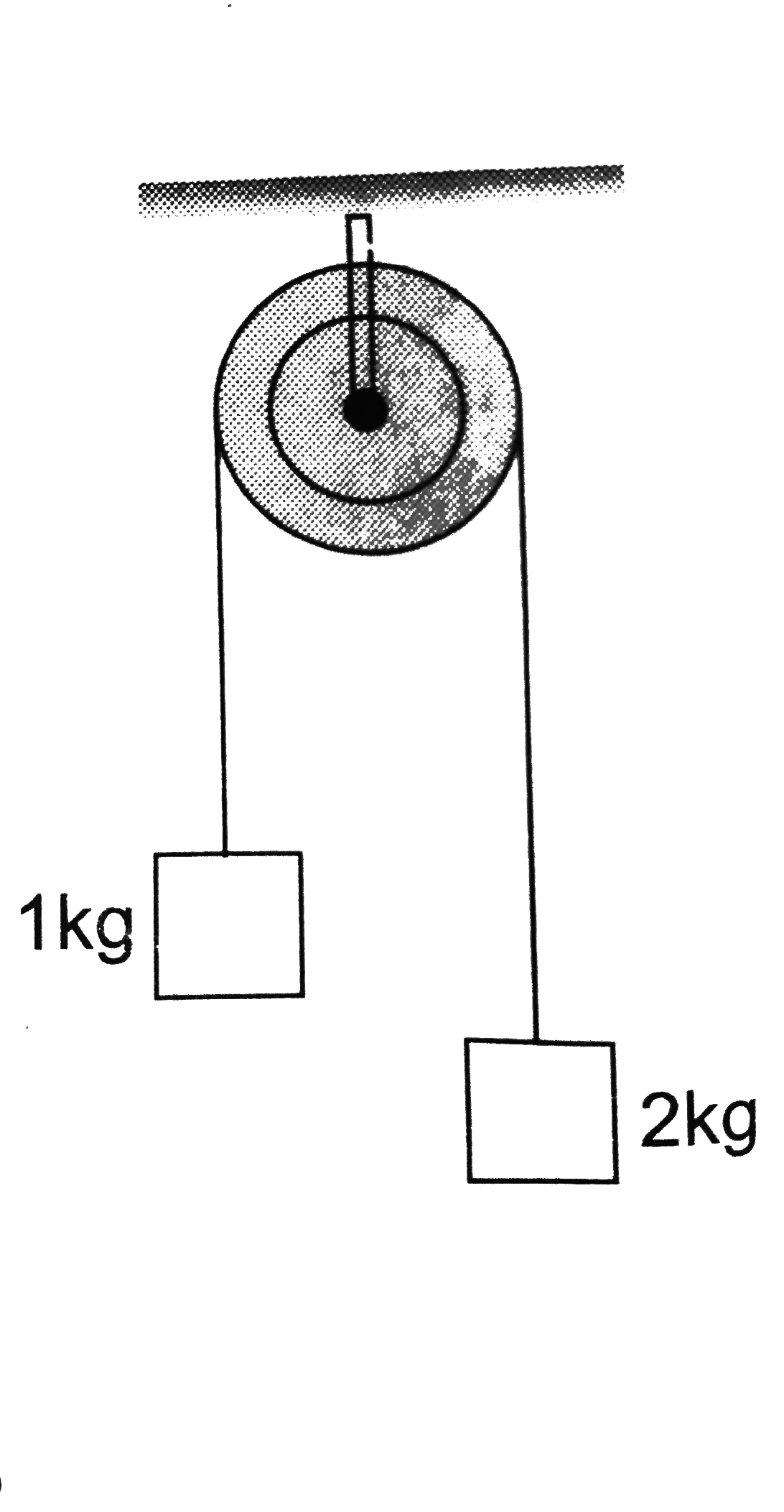
View SolutionTwo unequal masses are connected on two sides of a light and smooth pulley as shown in figure. The system is released from rest. The larger mass is stopped `1.0` second after the system is set into motion and then released immediately. The time elapsed before the string is tight again is: Take `g=10m//s^(2)`
View SolutionIn the figure, `m_(1)` is at rest, find the relation among `m_(1),m_(2)` and `m_(3)` ? .
View SolutionBy what acceleration the boy must go up so that `100kg` block remains stationary on the wedge. The wedge is fixed and is smooth `(g =10m//s^(2))`
 .
.
View SolutionThe system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.

View SolutionIn the adjacent figure, masses of `A,B` and `C` are `1kg ,3kg` and `2kg` respectively.Find
(a) the acceleration of the system and
(b) tension in the strings.
Neglect friction.`(g=10m//s^(2))`

View SolutionFind the relation between velocity of rod and that of wedge at any instant
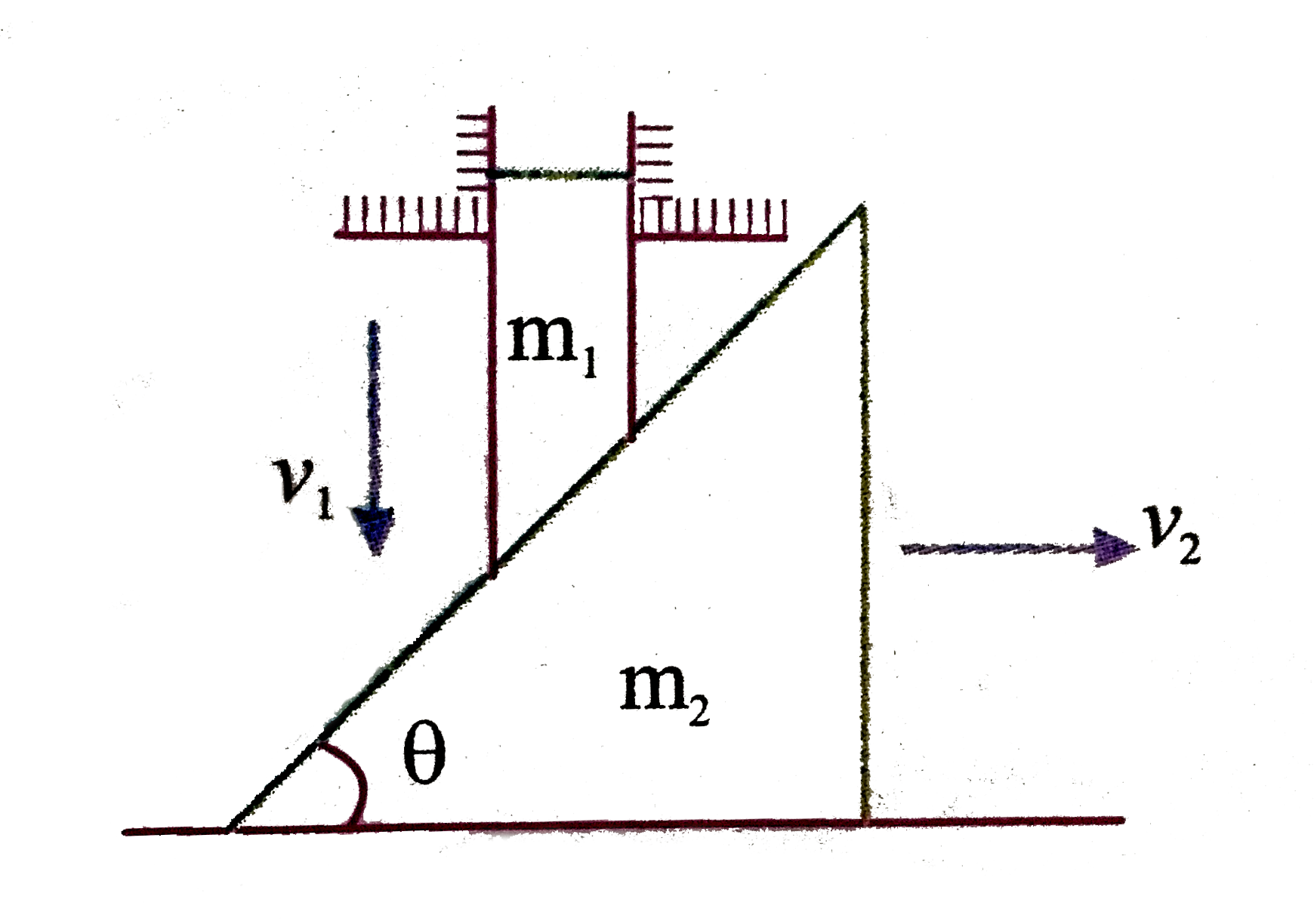 .
.
View SolutionFind the relation between `a_(1)` and `a_(2)`
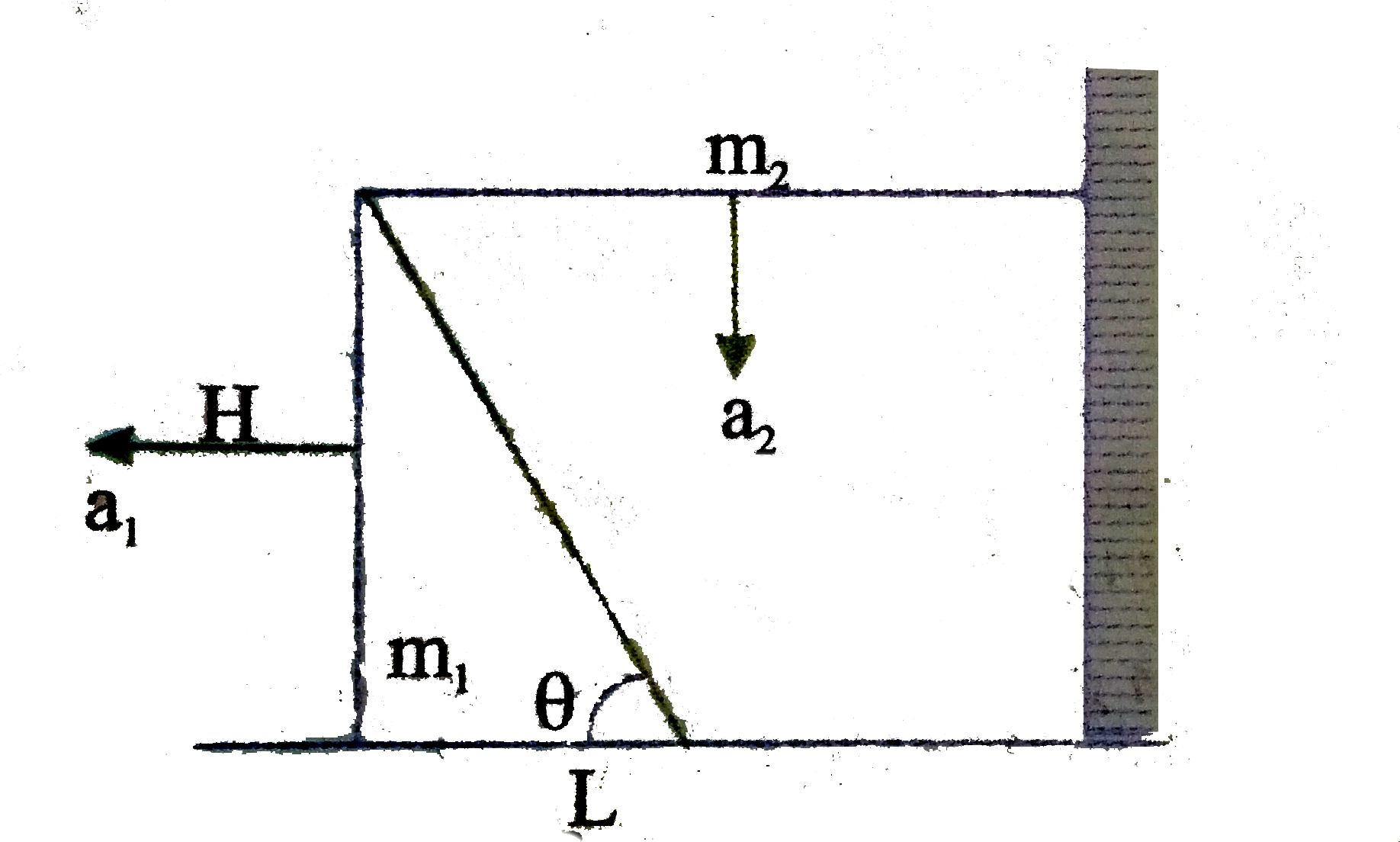 .
.
View SolutionA rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity `v_(1)` what is the velocity of end `B` at the instant when rod makes 'theta' angle with the horizontal .
View SolutionIn the fig, find the acceleration of mass `m_(2)` .
View SolutionIn the fig, find the acceleration of `m_(1)` and `m_(2)`
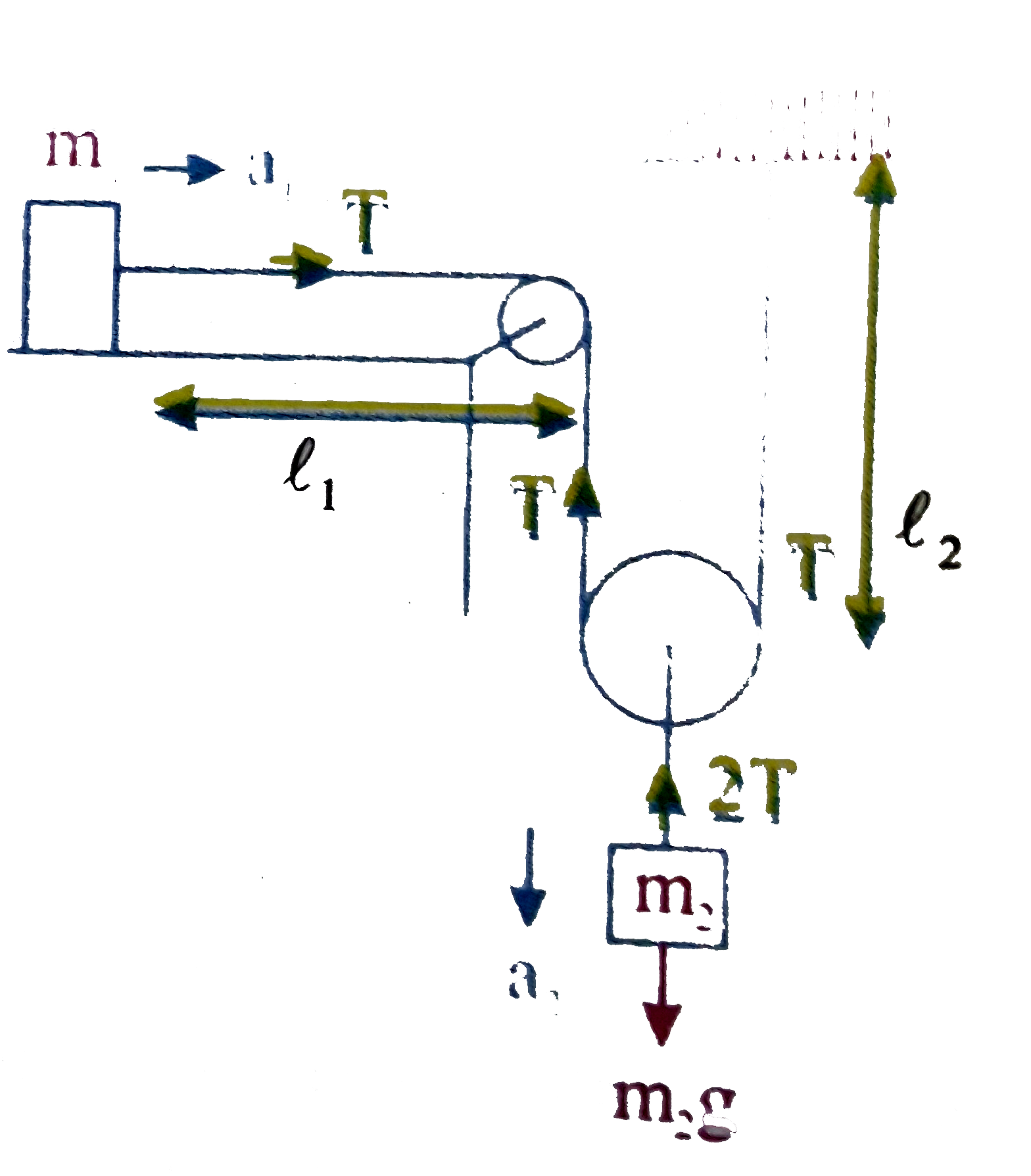 .
.
View SolutionA pedulum is hanging from the ceiling of a car having an acceleration `a_(0)` with respect to the road Find the angle made by the string with vertical at equilibrium Also find the tension in the string in this position
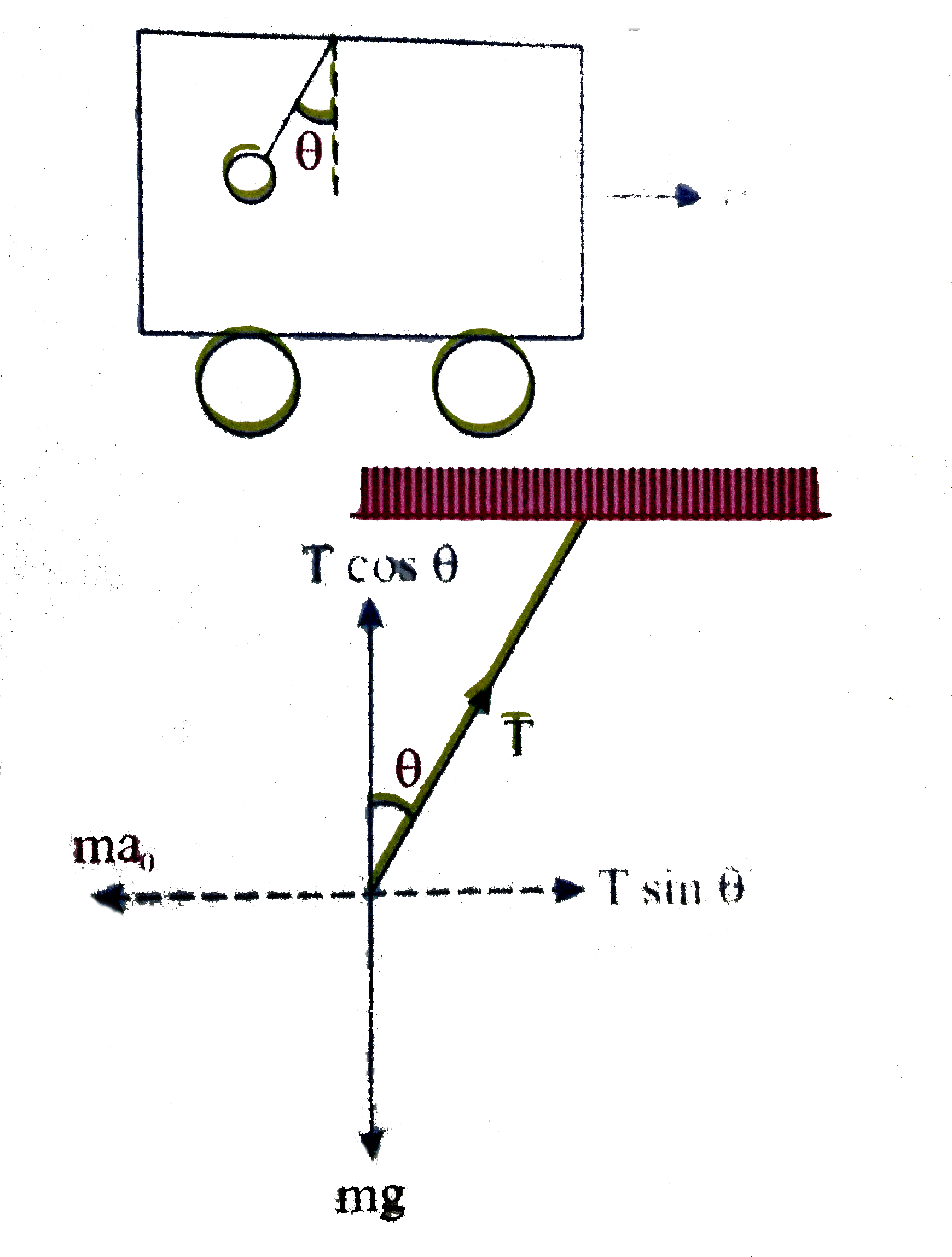 .
.
View SolutionFor what value of 'a' the block falls freely ?
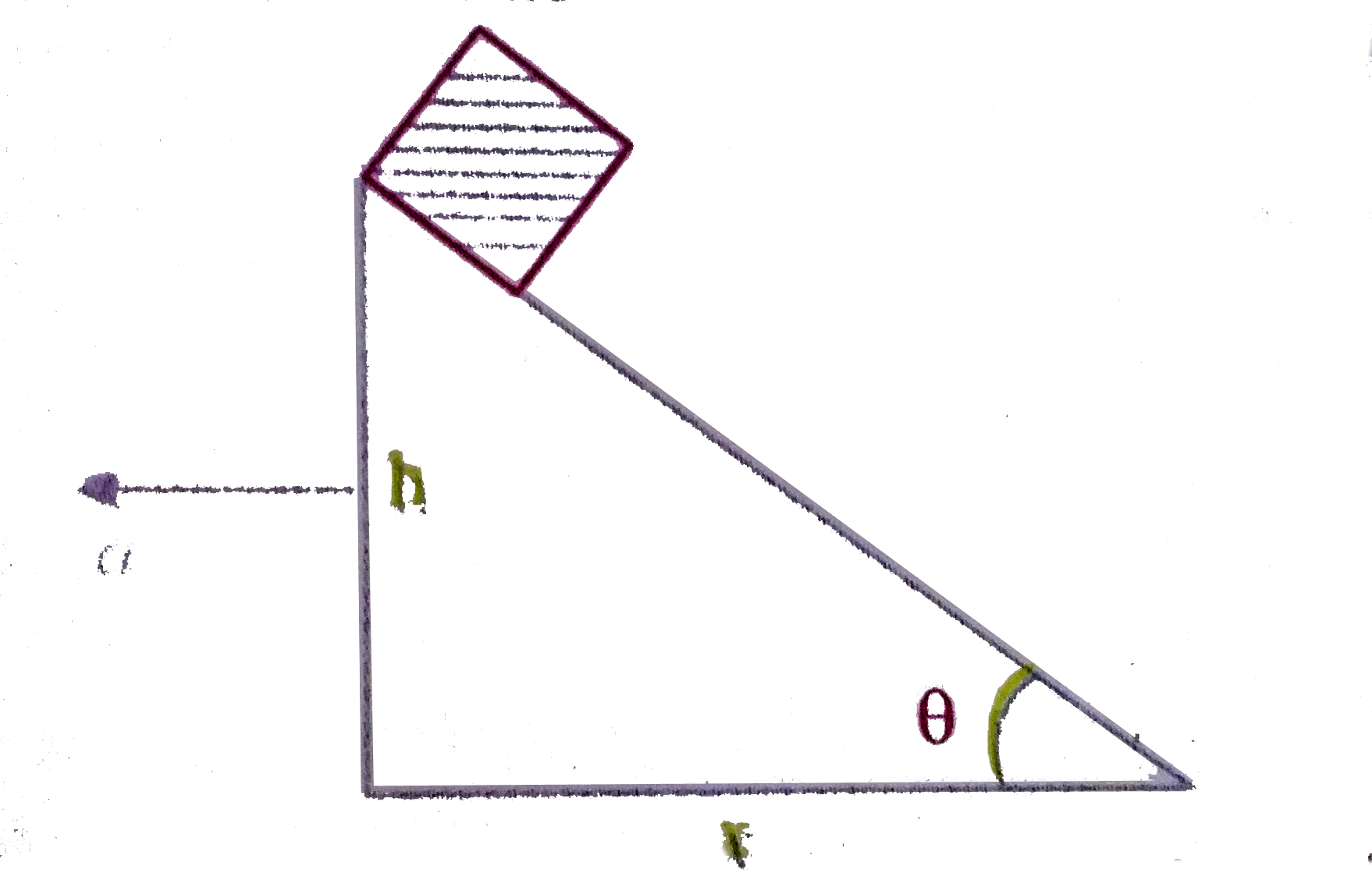 .
.
View SolutionA block of mass m is placed on a smooth wedge of inclination. The whole system is accelerated horizontally so that block does not slip on the wedge Find the i) Acceleration of the wedge Force to be applied on the wedge Force exerted by the wedge on the block .
View SolutionTwo fixed frictionless inclined plane making angles `30^(@)` and `60^(@)` with the vertical are shown in the figure. Two blocks A and B are placed on the two planes What is the relative vertical acceleration of A with respect to B ?

View SolutionFor what value of 'a' block slides up the plane with an acceleration 'g' relative to the inclined plane
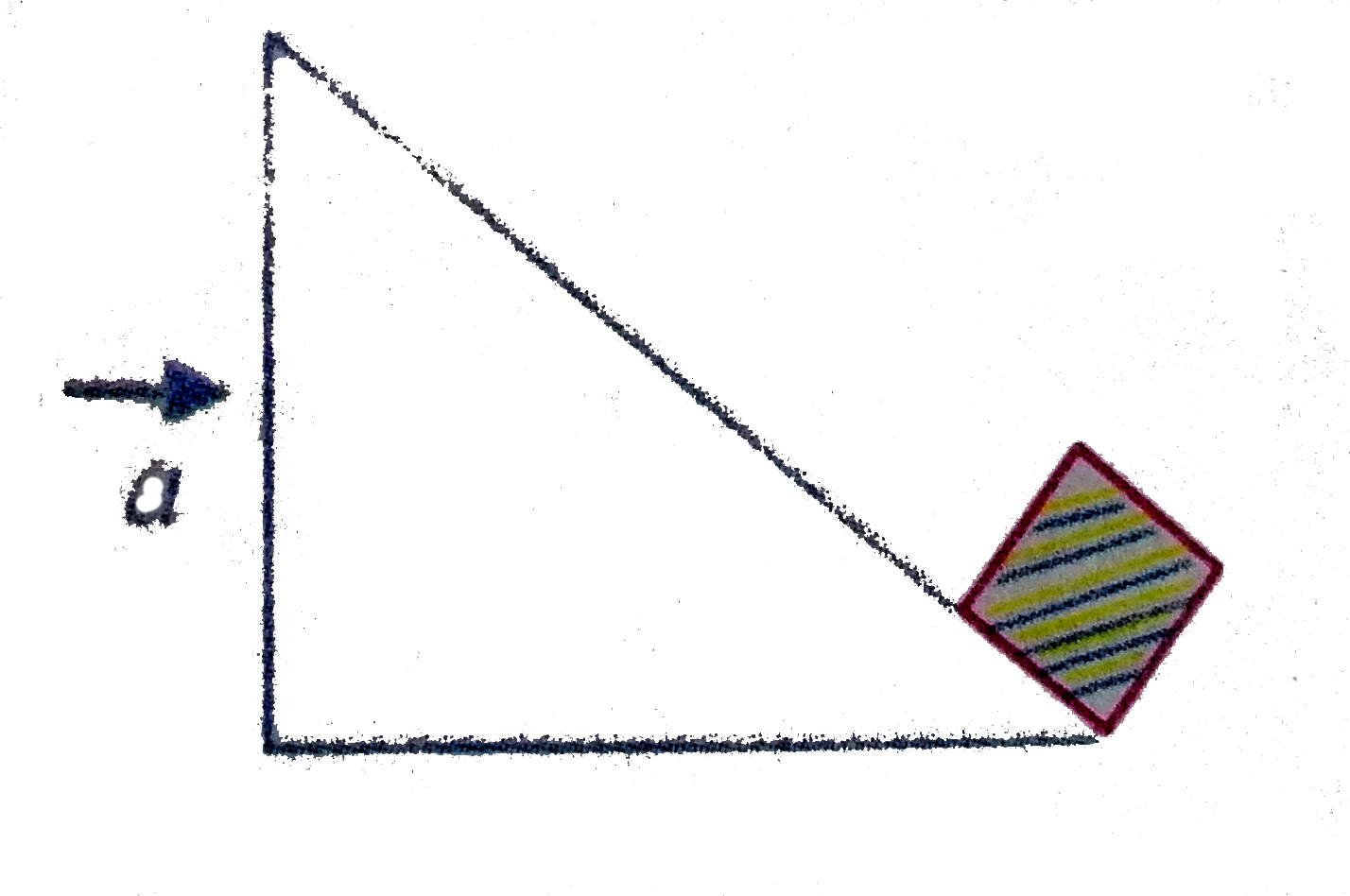 .
.
View SolutionA solid sphere of mass of `2kg` rests inside a cube as shown The cube is moving with ve-locity `vecv = (5thati+2thatj)ms^(-1)` where 't' is in sec and 'v' is in m/s What force does sphere exert on cube
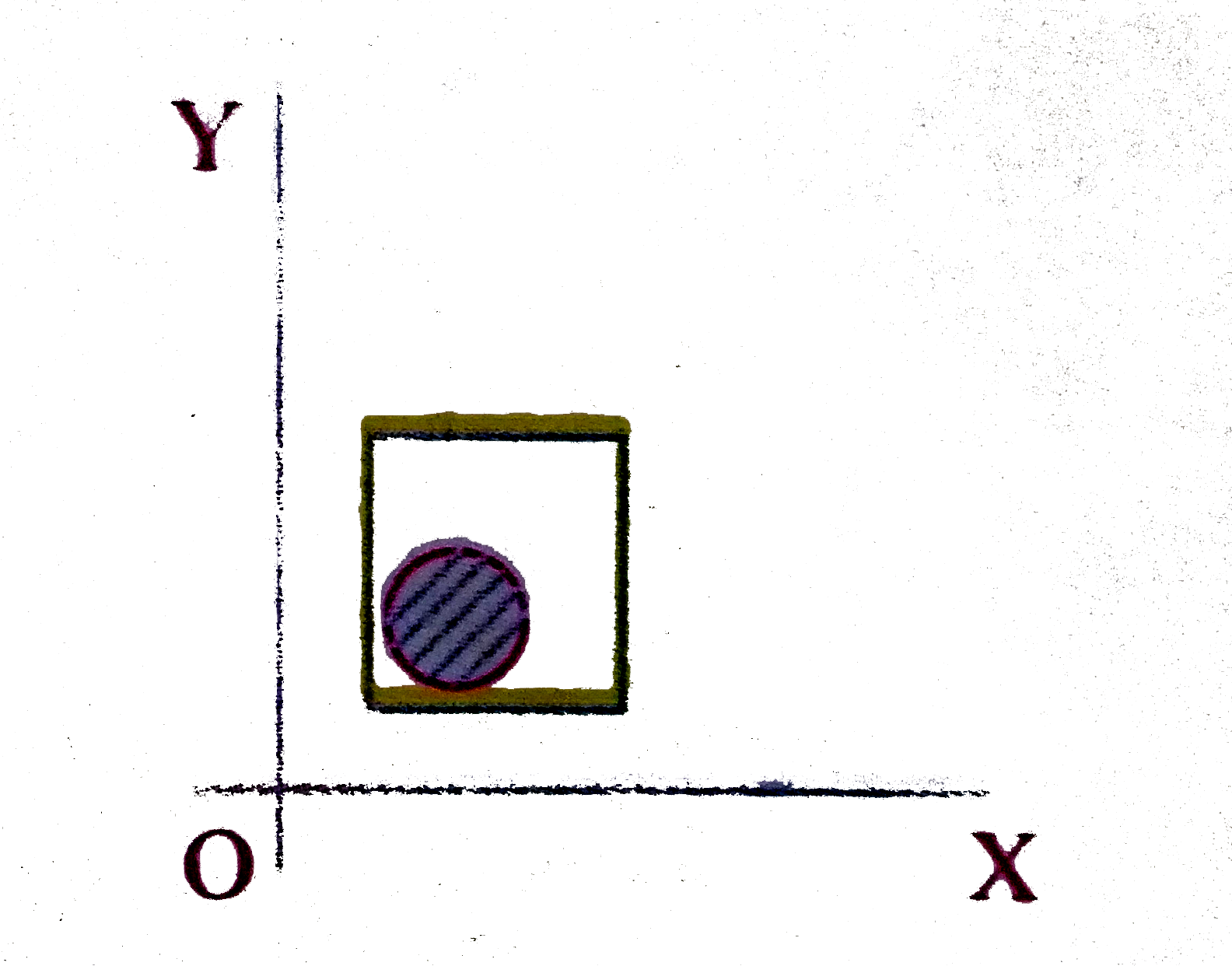 .
.
View SolutionA block is placed on an inclined plane moving towards right with an acceleration `a_(0) =g` The length of the inclined plane is `l_(0)`. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
 .
.
View SolutionA pendulum of mass m hangs from a support fixed to a trolley. The direction of the string when the trolley rolls up a plane of inclination `alpha` with acceleration `a_(0)` is

View SolutionA block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration `a_(0)` The base of incline hs length `L` Find the time taken by the block to reach the bottom
 .
.
View SolutionA bomb moving with velocity `(40i+50j-25k)m//s` explodes into two pieces of mass ratio 1:4. After explosion the smaller piece moves away with velocity `(200i +70j +15k)m//s`. The velocity of larger piece after explosion is .
View SolutionA particle of mass `4m` explodes into three pieces of masses m,m and `2m` The equal masses move along X-axis and Y-axis with velocities `4ms^(-1)` and `6ms^(-1)` respectively. The magnitude of the velocity of the heavier mass is
View SolutionA rifle of `20kg` mass can fire 4 "bullets"//"s". The mass of each bullet is `35 xx 10^(-3) kg` and its final velocity is `400ms^(-1)`., Then what force must be applied on the rifle so that it does not move backwards while firing the bullets ? .
View SolutionAll surfaces are smooth Find the horizontal displacements of the block and the wedge when the block slides down from top to bottom
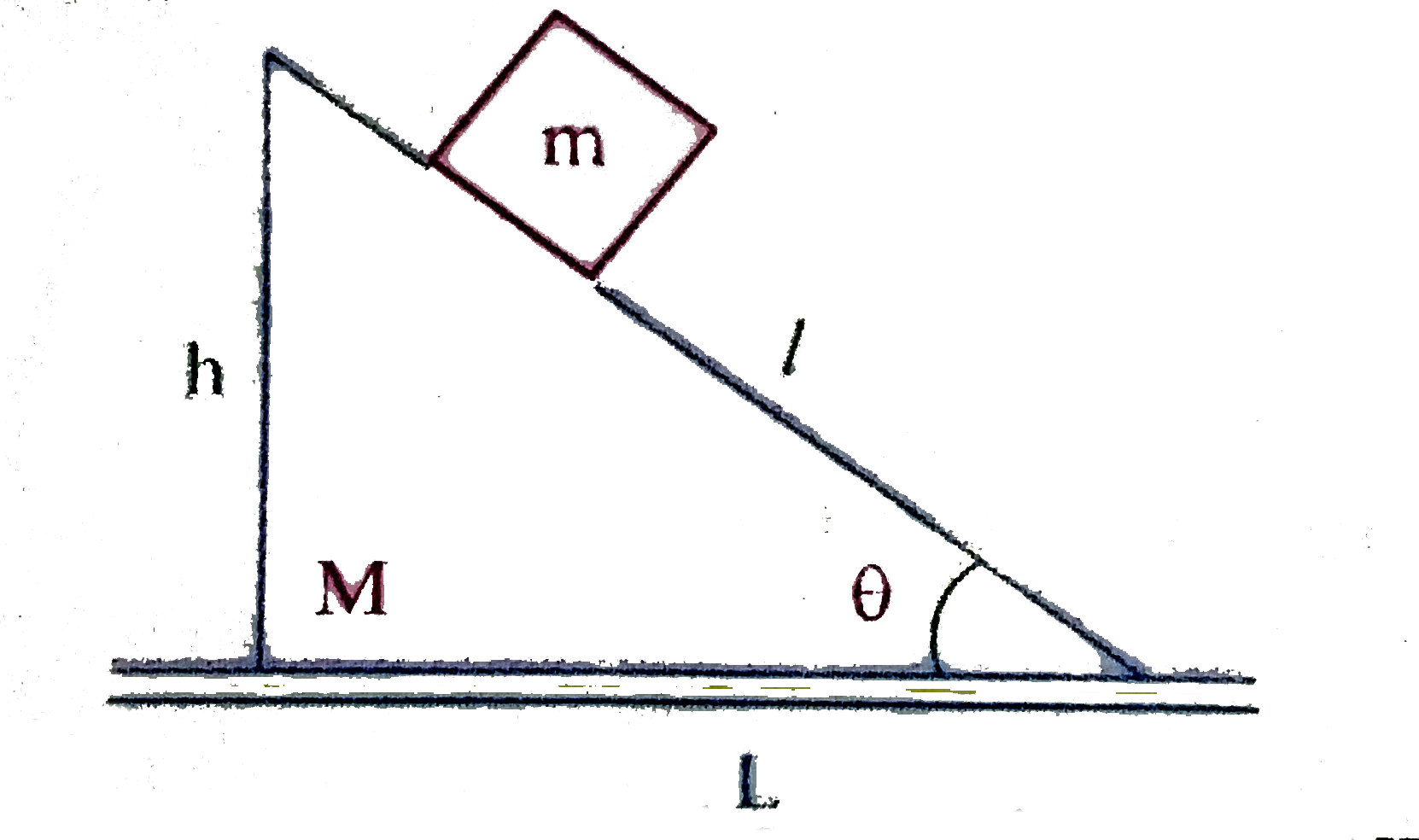 .
.
View SolutionA bomb of mass `1 kg` is thrown vertically upwards with a speed of `100m//s`. After 5 seconds, it explodes into two fragments. One fragment of mass `400 gm` is found to go down with a speed of `25m//s`. What will happen to the second fragment just after the explosion ? `(g=10ms^(-1))`
View SolutionA particle of mass `2m` is projected at an angle of `45^@` with horizontal with a velocity of `20sqrt2m//s`. After `1s` explosion takes place and the particle is broken into two equal pieces. As a result of explosion one part comes to rest. Find the maximum height attained by the other part. Take `g=10m//s^2`.
View SolutionA man of mass `40kg` is at rest between the walls as shown in the If `'●'` between the man and the walls is `0.8` find the normal reactions exerted by the walls on the man .
View SolutionA `2kg` block is in contact with a vertical wall having coefficient of friction `0.5` between the surfaces. A horizontal force of `40N` is applied on the block at right angles to the wall. Another force of `15N` is applied on the plane of the wall and at right angles to `40N` force. Find the acclecration of the block .
View SolutionA block of mass `4kg` is placed on a rough horizontal plane A time dependent horizontal force `F =kt` acts on the block `(k =2N//s)`. Find the frictional force between the block and the plane at `t =2` seconds and `t =5` seconds `(mu =0.2)` .
View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .
.
View SolutionWhen a car of mass `1000kg` is moving with a veocity of `20ms^(-1)` on a rough horizontal road its engine is switched off. Hwo for does the car move before it comes to rest if the coefficient of kintic friction between the road and tyres of the car is `0.75` ? .
View SolutionA horizontal conveyor belt moves with a constant velocity `V.A` small block is projected with a velocity of `6m//s` on it in a direction opposite to the direction of motion of the belt The block comes to rest relative to the belt in a time `4s. mu =0.3, g =10 .m//s^(2)` Find `V` .
View SolutionThe rear side of a truck is open. A box of `40kg` mass is placed `5m` away from the open end as shown in figure. The coefficient of friction between the box and the surface is `0.15`. On a straight road, the truck starts from rest and accel erating with `2m//s^(2)`. At what distance from the starting point does the box fall off the truck? Ignore the size of the box
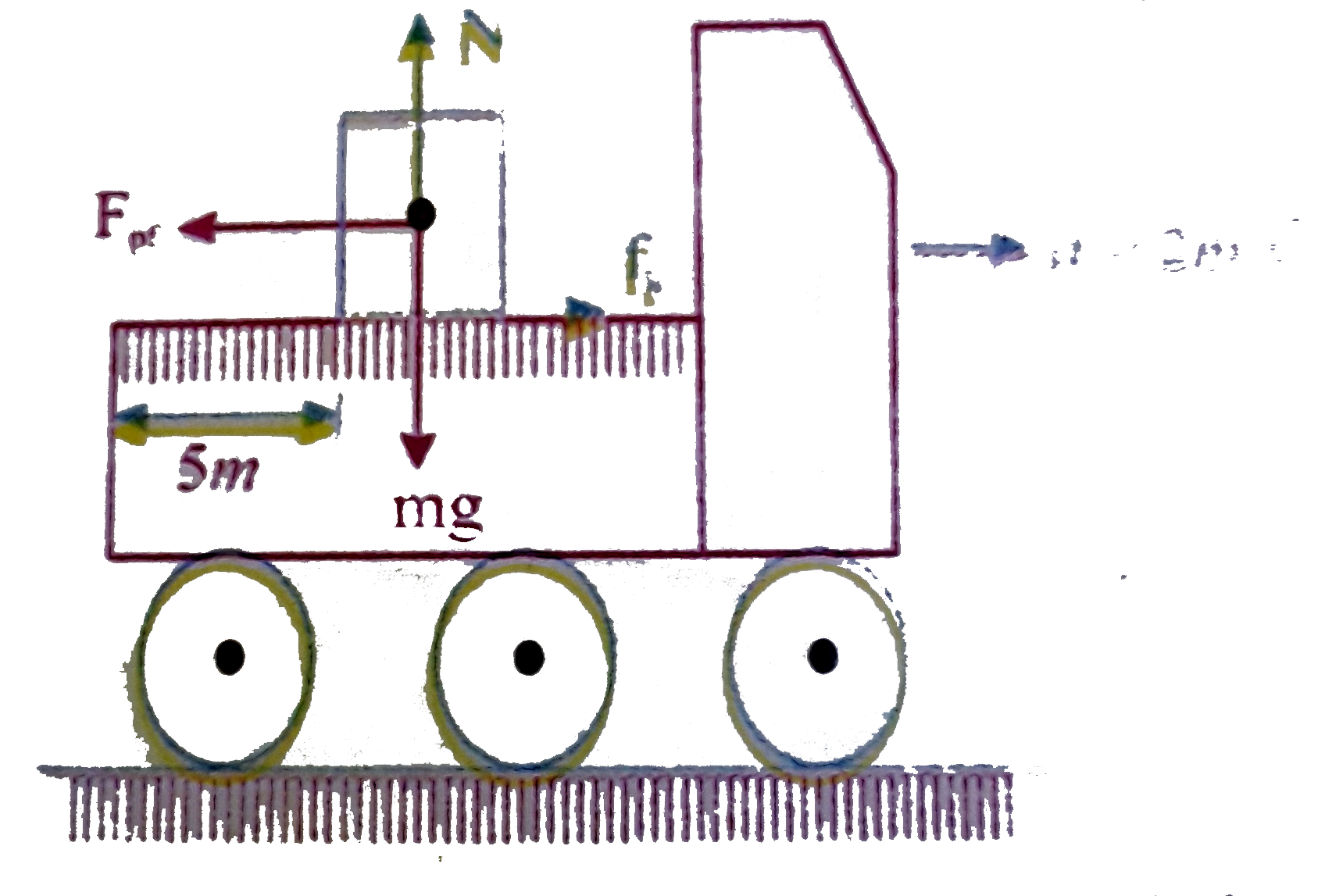
View SolutionA block of mass `10kg` is pushed by a force `F` on a horizontal rough plane is moving with acceleration `5ms^(-2)` When force is doubled its acceleration becomes `18ms^(-2)` Find the coefficient of friction between the block and rough horizontal plane `(g =10ms^(-2))` .
View SolutionA block of mass `'m'` is placed on a rough surface with a vertical cross section of `y =(x^(3))/(6)`. If the coefficient of friction is `0.5`, the maximum height above the ground at which the block can be placed without slipping is .
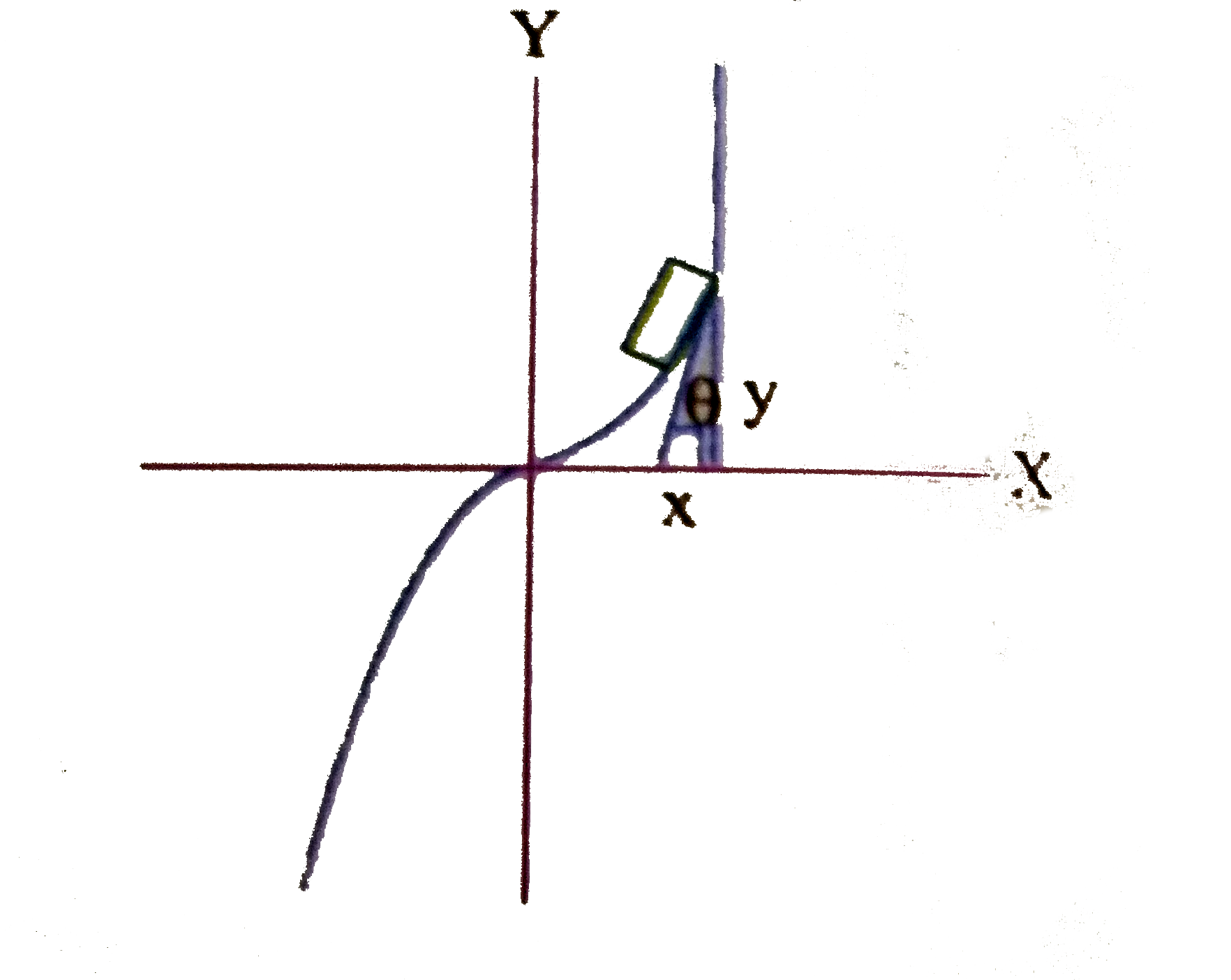
View SolutionA body is moving down a long inclined plane of angle of inclination `'theta`' for which the coefficient of friction varies with distance x as `mu`(x) = kx , where k is a constant . Here x is the distance moved by the body down the plane . The net force on the body will be zero at a distance `x_(0)` is given by ..........
View SolutionA body of mass 'm' slides down a smooth inclined plane having an inclination of `45^(@)` with the horizontal . It takes 2 s to reach the bottom . If the body is placed on a similar plane having coefficient of friction `0.5` , then what is the time taken for it to reach the bottom ?
View SolutionTwo blocks of masses 4 kg and 2 kg are in contact with each other on an inclined plane of inclination `30^(@)` as shown in the figure . The coefficient of friction between 4 kg mass and the inclined plane is `0.3` , whereas between 2 kg mass and the plane is `0.2` . find the contact force between the blocks .

View SolutionA `30kg` box has to move up an inclined plane of slope `30^(@)` the horizontal with a unform velocity of `5 ms^(-1)`. If the frictional force retarding the motion is `150N`, the horizontal force required to move the box up is `(g =ms^(-2))` .
View SolutionA body is sliding down an inclined plane having coefficient of friction 0.5. If the normal reaction is twice that of resultant downward force along the inclined plane, then find the angle between the inclined plane and the horizontal .
View SolutionIn the given the wedge is acted upon by a constant horizontal force 'F'. The wedge is moving on a smooth horizontal surface A ball of mas 'm' is at rest relative to the wedge The ratio of forces exerted on 'm' by the wedge when 'F' is acting and 'F' is withdrawn assuming no friction between the edge and the ball is equal to .
View SolutionA block of mass m kg is pushed up against a wall by a force `P` That makes an angle 'theta' with the horizontal as shown in The coefficient of static friction between the block and the wall is `mu` The minimum value of `P` that allows the block to remain stationary is .
View SolutionA block the of mass `4kg` is placed on another block of mass `5kg` and the block `B` rests on a smooth horizontal table for sliding the block `A` on `B` a horizontal force `12N` is required to be applied force on it How much maximum horizontal force can be applied on 'B' s that both `A` and `B` move together? Also find out the accleration proudced by this force
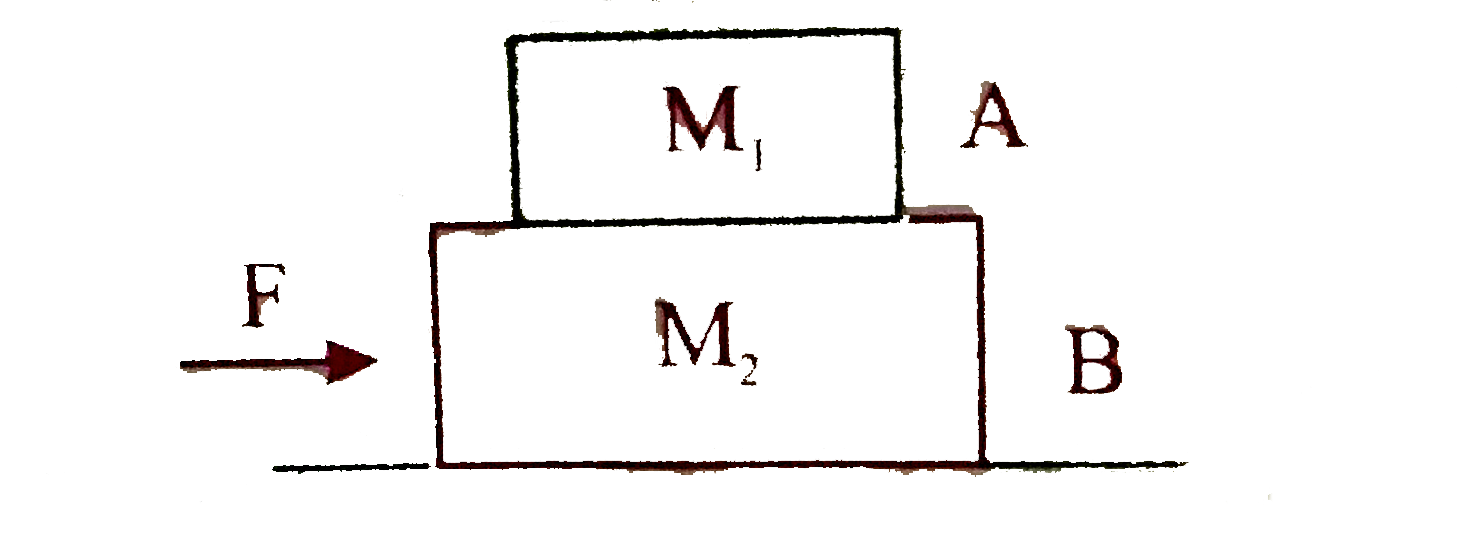 .
.
View SolutionTwo blocks of masses 'm' and and 'M' are arranged as shown in the The coefficient of friction between the two blocks is `'mu'`, where as between the lower block and the horizontal surface is zero. Find the force 'F' to be applied on the upper block for the system to be under equilibrium ? .

View SolutionBlock A weighs `4 N` and block weigh `8 N` The coefficient of kinetic friction is `0.25` for all surface find the force `F` to slide `B` at a constant speed when (a)`A` rest on `B` and moves with it (b) `A` is held at rest and (c )`A and B` are connected by a light cord passing over a smooth putting as shown in fig 7.31 (a - c) restively.

View SolutionTwo cars of masses `m_(1)` and `m_(2)` are moving in circles of raddii `r_(1)` and `r_(2)` respectively. Their speeds are such that they make complete circle in the same time t The ratio of their centripetal acceleration is .
View SolutionA car is driven round a curved path of radius `18m` without the danger of skidding The coefficeient of friction between the tyres of the car and the surface of the curved path is 0.2 What is the maximum speed in kmph of the car for safe driving ? `(g =10 ms^(-2))` .
View SolutionA point P moves in counter-clockwise direction on figure. The movement of P is such that it sweeps out a length `s=t^(3)+5`, where s is in metre and t is in second. The radius of the pathh is 20 m. the acceleration of P when t=2s is nearly
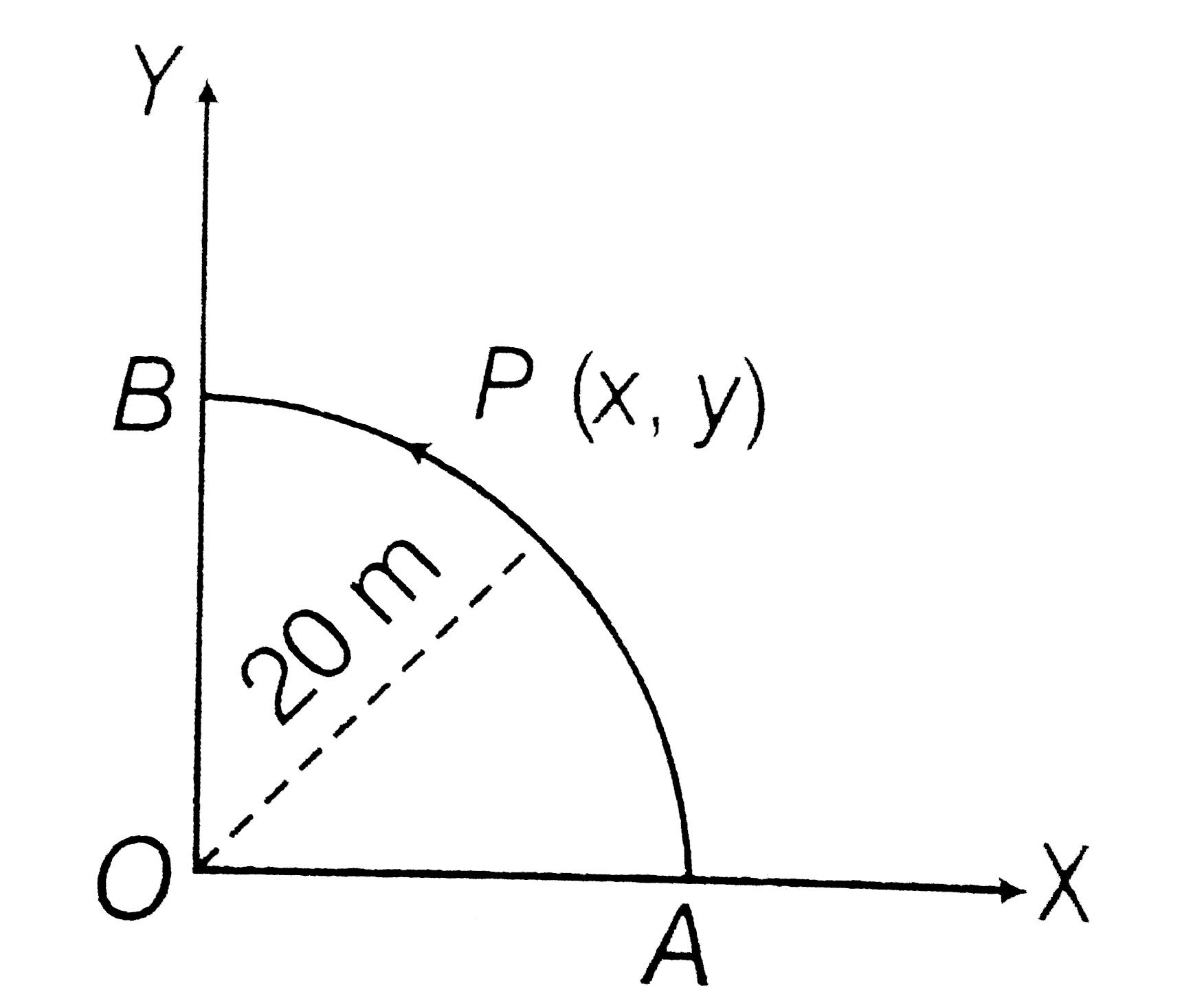
View SolutionA turn of radius `20 m` is banked for the vehicle of mass `200 kg` going at a speed of `10 m//s`. Find the direction and magnitude of frictional force (a) `5 m//s`
(b) `15 m//s`
Assume that friction is sufficient to prevent slipping. `(g=10 m//s^(2))`
View Solution
Solved Example questions and complete solutions for chapter NEWTONS LAWS OF MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11