Complete Solutions to LEVEL -II (C.W) of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| NARAYANA | LEVEL -II (C.W) |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
The momenta of a body in two perpendicular directions at any time 't' are given by `P_(x)=2t^(2) +6` and `P_(y)=(3t^(2))/(2)+3`. The force acting on the body at `t =2` sec is .
View SolutionWhen a force F acs on a body of mass m the acceleration product in the body is a . If htree equal forces `F_(1)=F_(2)=F_(3)=F` act on the same body as shown in figure the accleration produced is
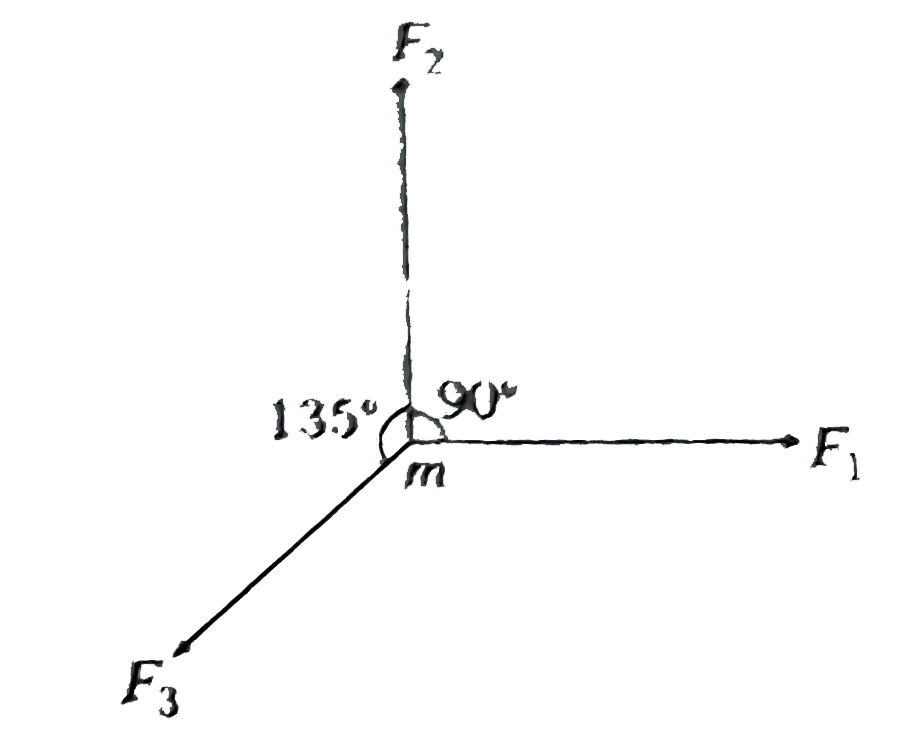
View SolutionTwo blocks of masses m and `M` are placed on a horizontal frictionless table connected by light spring as shown in figure. The Mass M is pulled to the right with a force `F` It the acceleration of mass m is a then the acceleration of `M` will be .

View SolutionThe displacement of a body moving along a straight line is givne by `S =bt^(n)` where 'b' is a constant and 't' is time. For what value of 'n' the body moves under the action of constant force ? .
View SolutionIf `F =F_(0) (1-e^(-1//lambda))` the F-t graph is .`
View SolutionThree forces `20 sqrt(2)N,20 sqrt(2) N` and `40N` are acting along `X,Y` and `Z-`axes respectively on a `5sqrt2 kg` mass at rest at the origin. The magnitude of its displacement after `5s` is .
View SolutionA horizontal jet of water coming out of a pipe of area of cross-section `20cm^(2)` hits a vertical wall with a velocity of `10ms^(-1)` and rebounds with the same speed. The force exerted by water on the wall is .
View SolutionA rocket of mass `40kg` has `160kg` fuel. The exhaust velocity of the fuel is `2.0km//s`. The rate of consumption of fuel is `4kg//s`. Calculate the ultimate vertical speed gained by the rocket. `(g=10m//s^2)`
View SolutionA body of mass 5 kg starts from the origin with an initial velocity `vecu=30hati+40hatjms^(-1)`. If a constant force `vecF=-(hati+5hatj)N` acts on the body, the time in which the y-component of the velocity becomes zero is
View SolutionA professional diver of mass `60kg` performs a dive from a platform `10m` above the water surface. Find the magnitude of the average impact force experienced by him if the impact time is `1s` on collision with water surface. Assume that the velocity of the diver just after enering the water surface is `4ms^(-1)(g =10 ms^(-2))` .
View SolutionAn open knife edge of mass 200g is dropped from height 5m on a cardboar. If the knife edge penetrates a distance 2 m into the cardboard. Find the average resistance offered by the cardboar to the knife edge (in N). `(g = 10 m//s^(2))`

View SolutionSix forces lying in a plane and forming angles of `60^(@)` relative to one another are applied to the centre of a homogeneous sphere with a mass `m =6kg`. These forces are radially outward and consecutively `1N,2N,3N,4N,5N` and `6N` The acceleration of the sphere is .
View SolutionA particle of mass `m` , initially at rest , is acted upon by a variable force `F` for a brief interval of time `T`. It begins to move with a velocity `u` after the force stops acting . `F` is shown in the graph as a function of time. The curve is a semicircle.

View SolutionA ball of mass `0.2kg` strikes an obstacle and moves at `60^(@)` to its original direction If its speed also changes from `20m//s` to `10m//s`, the magnitude of the impulse received by the ball is .
View SolutionThe block is placed on a frictionless surface in gravity free space. A heavy string of a mass m is conncected and force `F` is applied on the string then the tension at the middle of rope is
 .
.
View SolutionA ball is suspended by a thread from the ceiling of a tram car. The brakes are applied and the speed of the car changes uniformly from `36 kmh^(-1)` to zero is `5s`. The angle by which the ball deviates from the vertical is `(g =10ms^(-2))` .
View SolutionA block is kept on a frictionless inclined surface with angle of inclination `alpha`. The incline is given an acceeration 'a' to keep the block stationary Then 'a' is equal to
 .
.
View SolutionA man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs `1,000N` exerts a force of `450N` on the chair downwards while pulling the rope on the other side. If the chair weighs `250N` then the acceleration of the chair is .
View SolutionA balloon of mass `M` is descending at a constant acceleration `alpha`. When a mass m is released from the balloon it starts rising with the same acceleration `alpha` Assuming that its volume does not change what is the value of m. ?
View SolutionA monkey of mass `40kg` climbs on a massless rope of breaking strenght `600N`. The rope will break if the monkey (Take `g =10 m//s^(2)`) .
View SolutionTwo persons are holding a rope of negligible weight tightly at its ends so that it is horizontal. A `15kg` weight is attached to rope at the midpoint which now no more remains horizontal The minimum tension required to completely straighten the rope is .
View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View SolutionConsider three blocks of masses `m_(1),m_(2),m_(3)` interconnected by strings which are pulled by a common force `F` on a frictionless horizontal tabel as in the figure. The tension `T_(1)` and `T_(2)` are also indicated
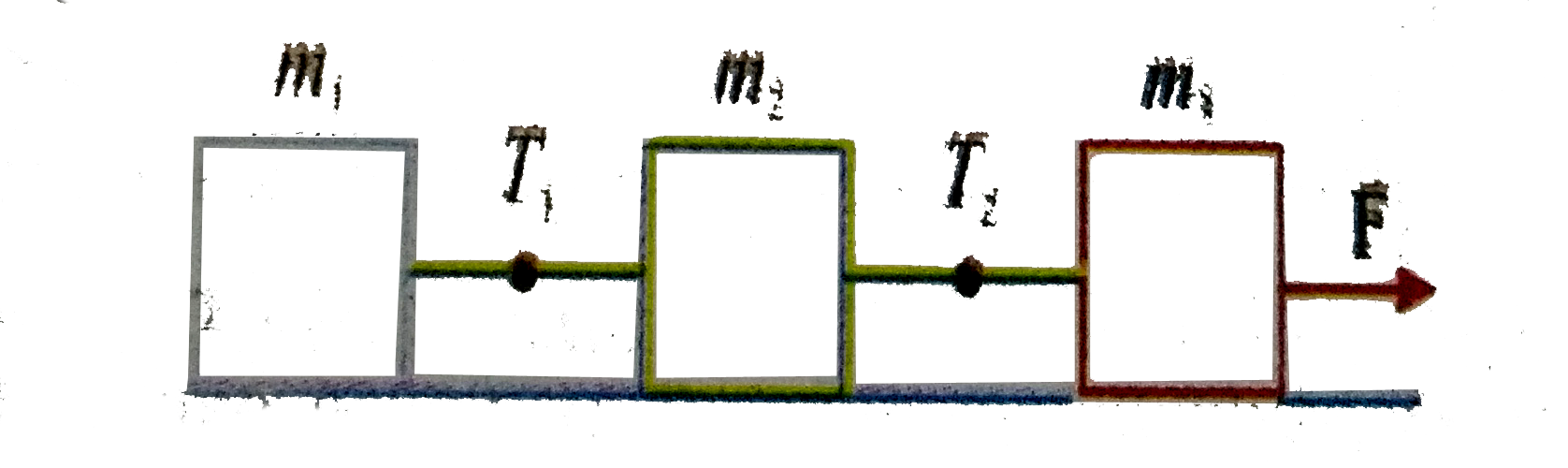 .
.
a) `T_(2)gtT_(1)` if `m_(2)gtm_(1)`
b)`T_(2)=T_(1)` if `m_(2)=m_(1)` , c) `T_(2) gt T_(1)` always
d) acceleration of the system `(F)/(m_(1)+m_(2)+m_(3))` .
View SolutionA railway engine of mass 50 tons is pulling a wagon of mass 40 tons with a force of `4500N`. The resistance force acting is `1N` per ton The tension in the coupling between the engine and the wagon is .
View SolutionIn the following figure, the pulley is massless and frictionless. There is no friction between the body and the floor. The acceleration produced in the body when it is displaced through a certain disatnace with force 'P' will be
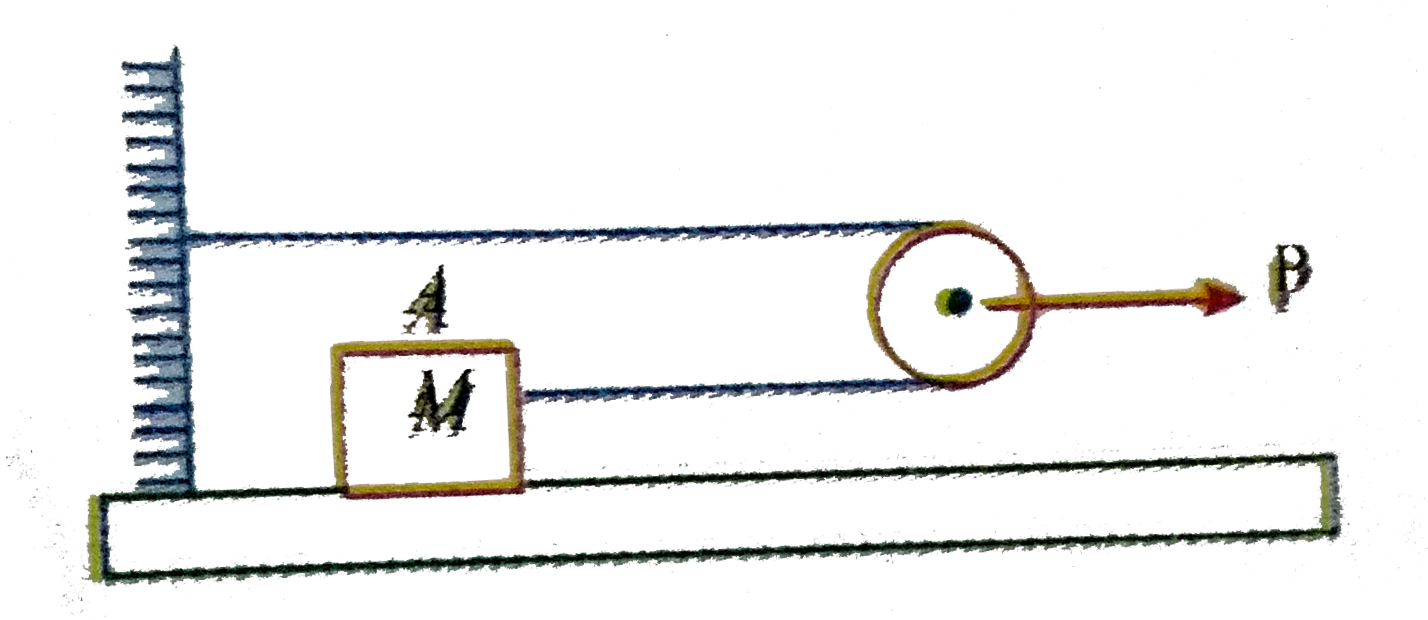 .
.
View SolutionTwo identical blocks each of mass ''M'' are tied to the ends of a string and the string is laid over a smooth fixed pulley. Initially the masses are held at rest at the same level. What fraction of mass must be removed from one block and added to the other, so that is has an acceleration of `1//5^(th)` of the acceleration due to gravity ? .
View SolutionIn the given arrangement, n number of equal masses are connected by stings of negligible masses. The tension in the string connected to `n^(th)` mass is
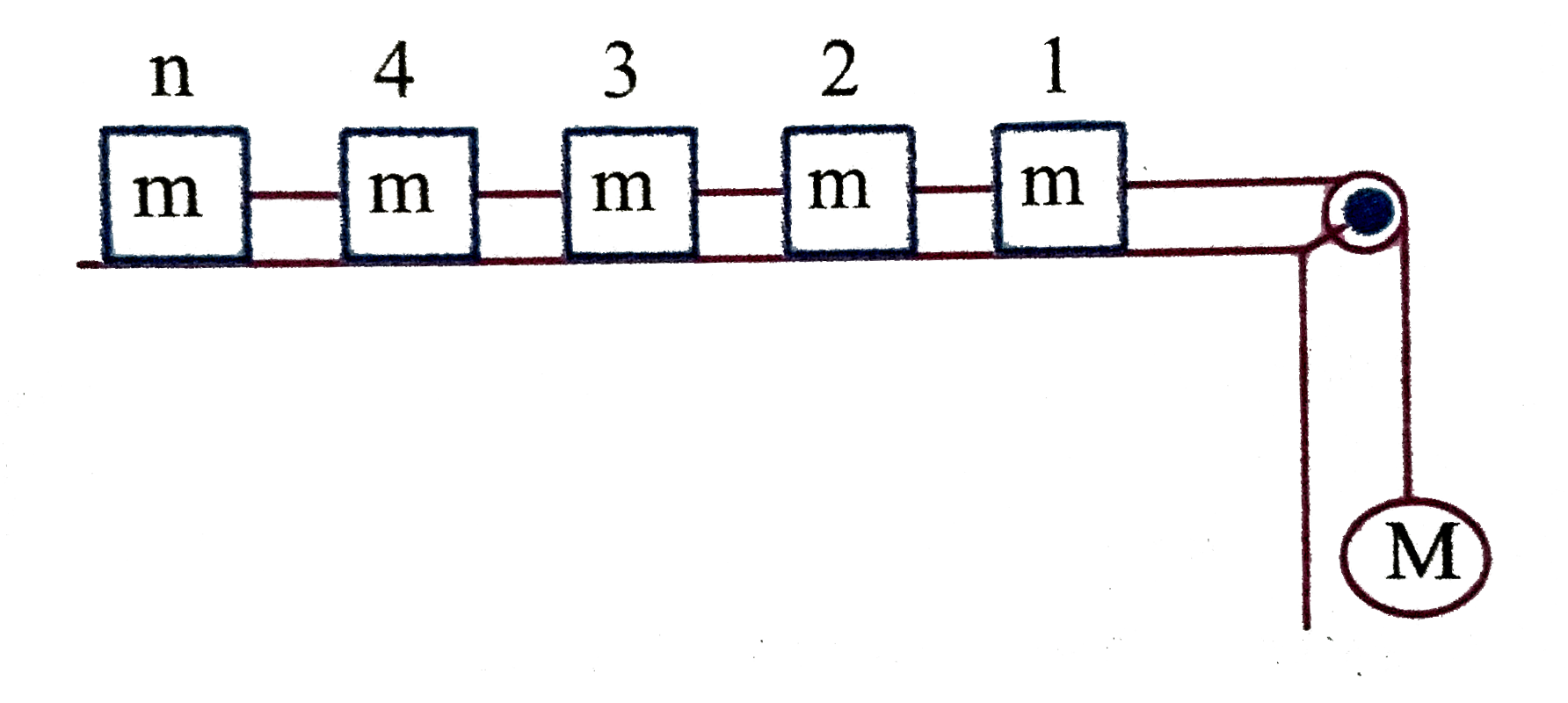 .
.
View SolutionA block weighing `4N` is supported by two ropes Once rope is horizontal and the other makes an angle of `30^(@)` with the ceilling The tension (in newton) in the rope attached to the ceilling is .
View SolutionThe pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case I the mass m is lifted by attaching a mass `2m` to the other end of rope with a constant downward force `F =2mg`, where g is acceleration due to gravity The acceleration of mass m in case I is
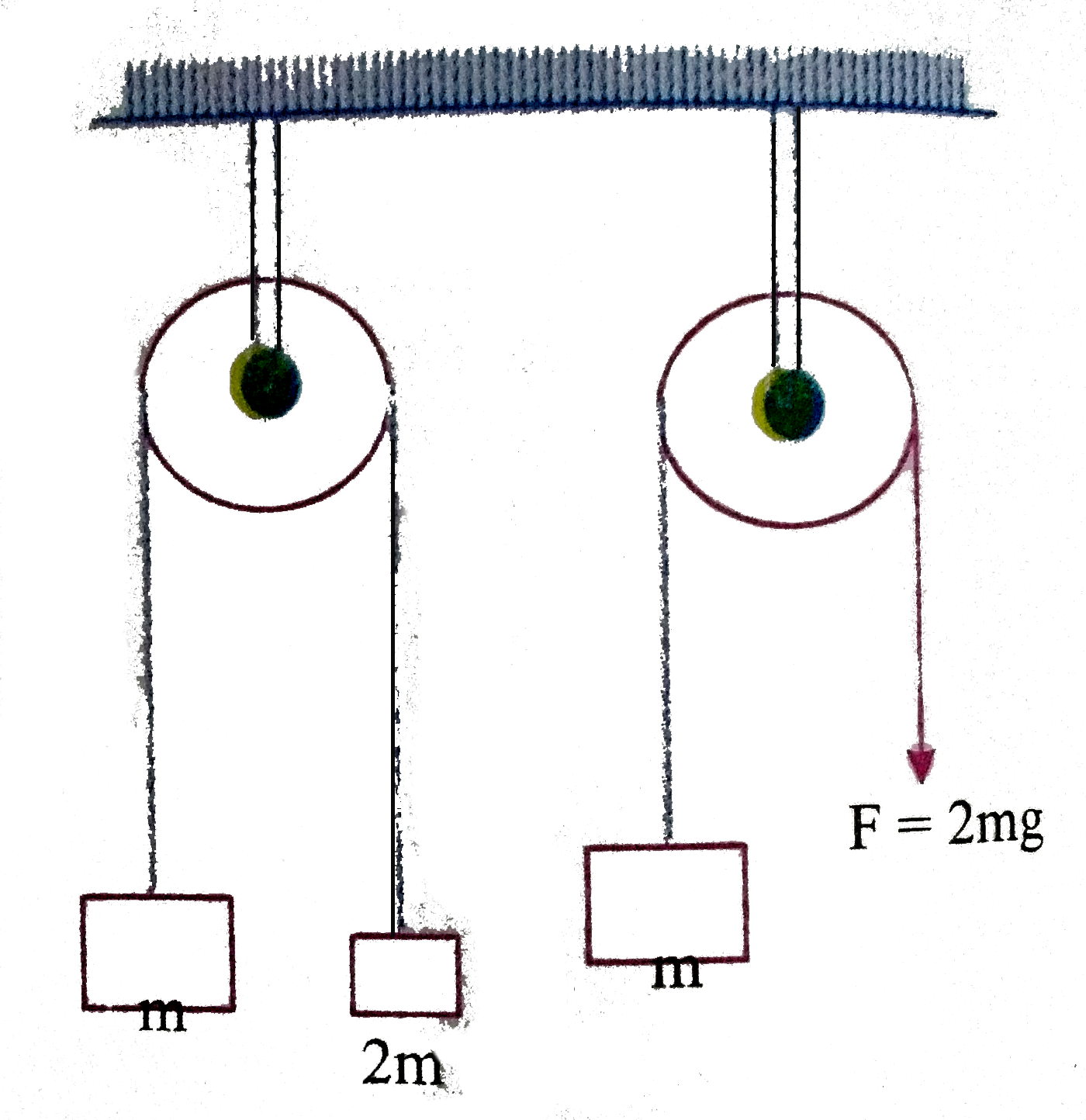 .
.
View SolutionTwo masses of `10kg` and `5kg` are suspended from a rigid support as shown in figure. The system is pulled down with a force of `150N` attached to the lower mass. The string attached to the support breaks and the system accelerates downwards
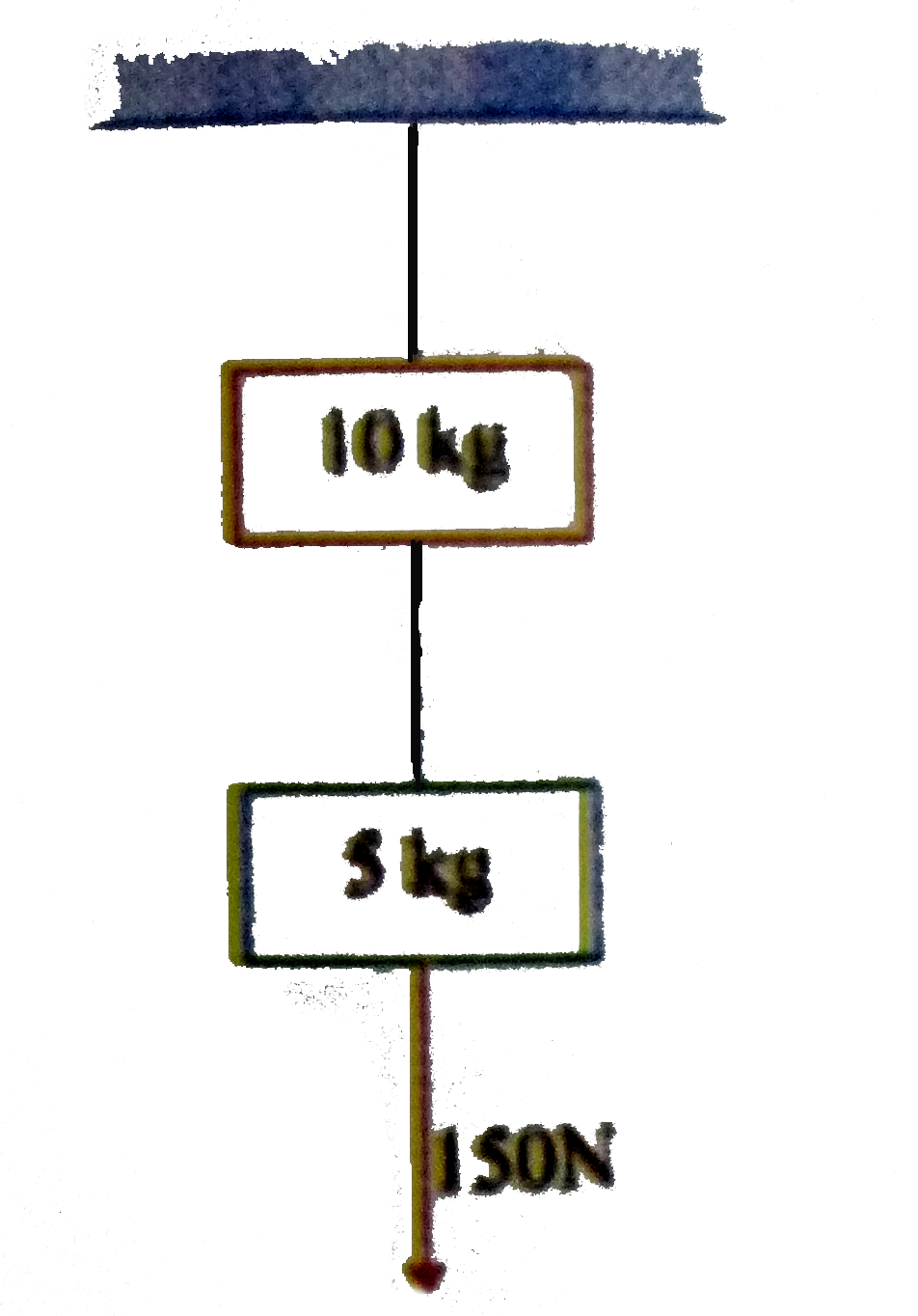
In case the force continues to act. what will be the tension acting between the two masses ? .
View SolutionTwo bodies of masses `3kg` and `2kg` are connected by a along string and the string is made to pass over a smooth fixed pulley Initially the bodies are held at the saem level and released from rest. The velocity of the `3kg` body after one second is `(g =10m//s^(2))` .
View SolutionA block of mass `3kg` which is on a smooth inclined plane making angie of `30^(@)` to the horizontal is connected by cord passing over light frictionless pulley to second block of mass `2kg` hanging vertically. What is the acceleration of each block and waht is the tension of the cord ? .
View SolutionIf `m_(1) =10kg,m_(2)=4kg,m_(3) =2kg`, the acceleration of system is
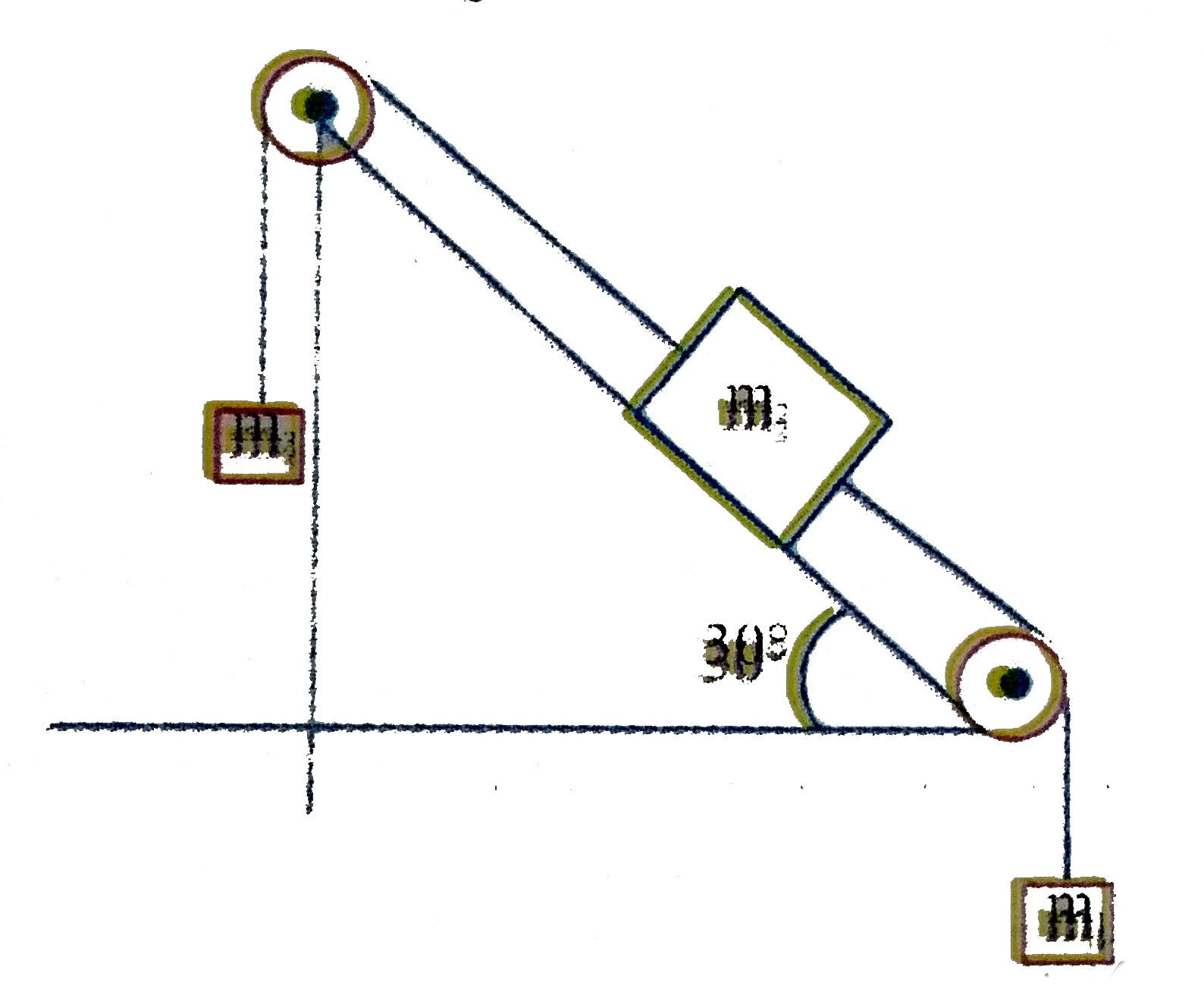 .
.
View SolutionThe string between blocks of mass m and 2m is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass 2m and m (immediately after cutting)

View SolutionAll surfaces are smooth The acceleration of mass m relative to the wedge is
 .
.
View SolutionA bullet of mass `10gm` moving with a horizontal velocity `100m//s` passes through a wooden block of mass `100gm`. The block is resting on a smooth horizontal floor. After passing through the block the velocity of the bullet is `10m//s` the velocity of the emerging bullet with respect to the block is .
View SolutionA shell is fired from the ground at an angle `theta` with horizontal with a velocity 'v'. At its highest point it breaks into two equal fragments. if one fragment comes back through its initial line of motion with same speed then the speed of the second fragment will be .
View SolutionTwo trolleys of mass `m` and `3 m` are attached by a spring. The spring was compressed and then released , they move off in opposite direction and comes to rest after covering distances `s_(1)` and `s_(2)` respectively. Assuming the coefficient of friction to be uniform , the ratio of distances `s_(1) : s_(2)` is
View SolutionTwo particles of masses `m_(1)` and `m_(2)` in projectile motion have velocities `vec(v)_(1)` and `vec(v)_(2)` , respectively , at time `t = 0`. They collide at time `t_(0)`. Their velocities become `vec(v')_(1)` and `vec(v')_(2)` at time ` 2 t_(0)` while still moving in air. The value of `|(m_(1) vec(v')_(1) + m_(2) vec(v')_(2)) - (m_(1) vec(v)_(1) + m_(2) vec(v)_(2))|`
View SolutionTwo masses `M_(1)` and `M_(2)` connected by means of a string which is made to pass over light, smooth pulley are in equilibrium on a fixed smooth wedge as shown in figure. If `theta =60^(@)` and `alpha =30^(@)` then the ratio of `M_(1)` to `M_(2)` is
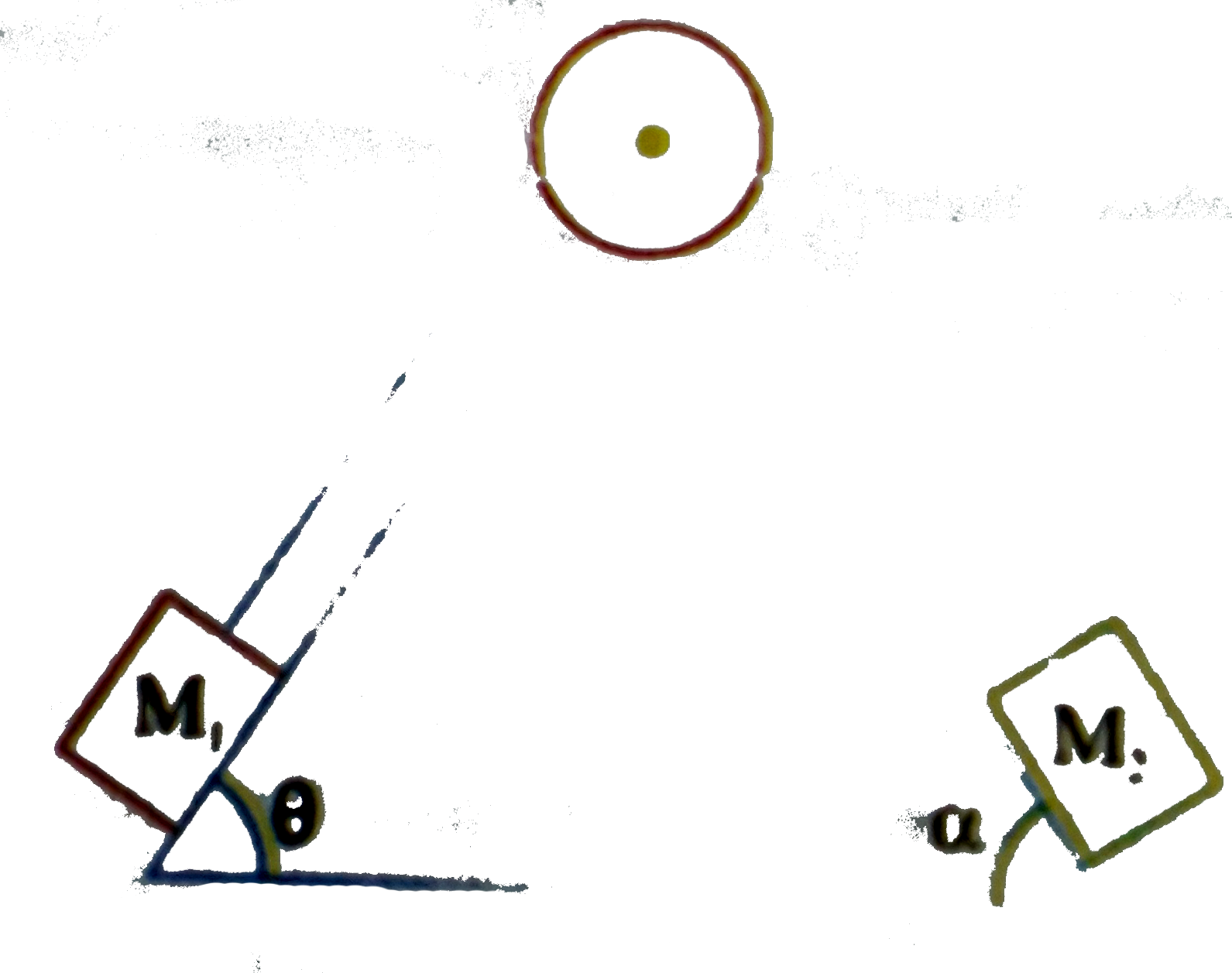 .
.
View SolutionIf `O` is at equilibrium then the values of the tension `T_(1)` and `T_(2)` are, (`20 N` is acting vertically downwards at `O`).
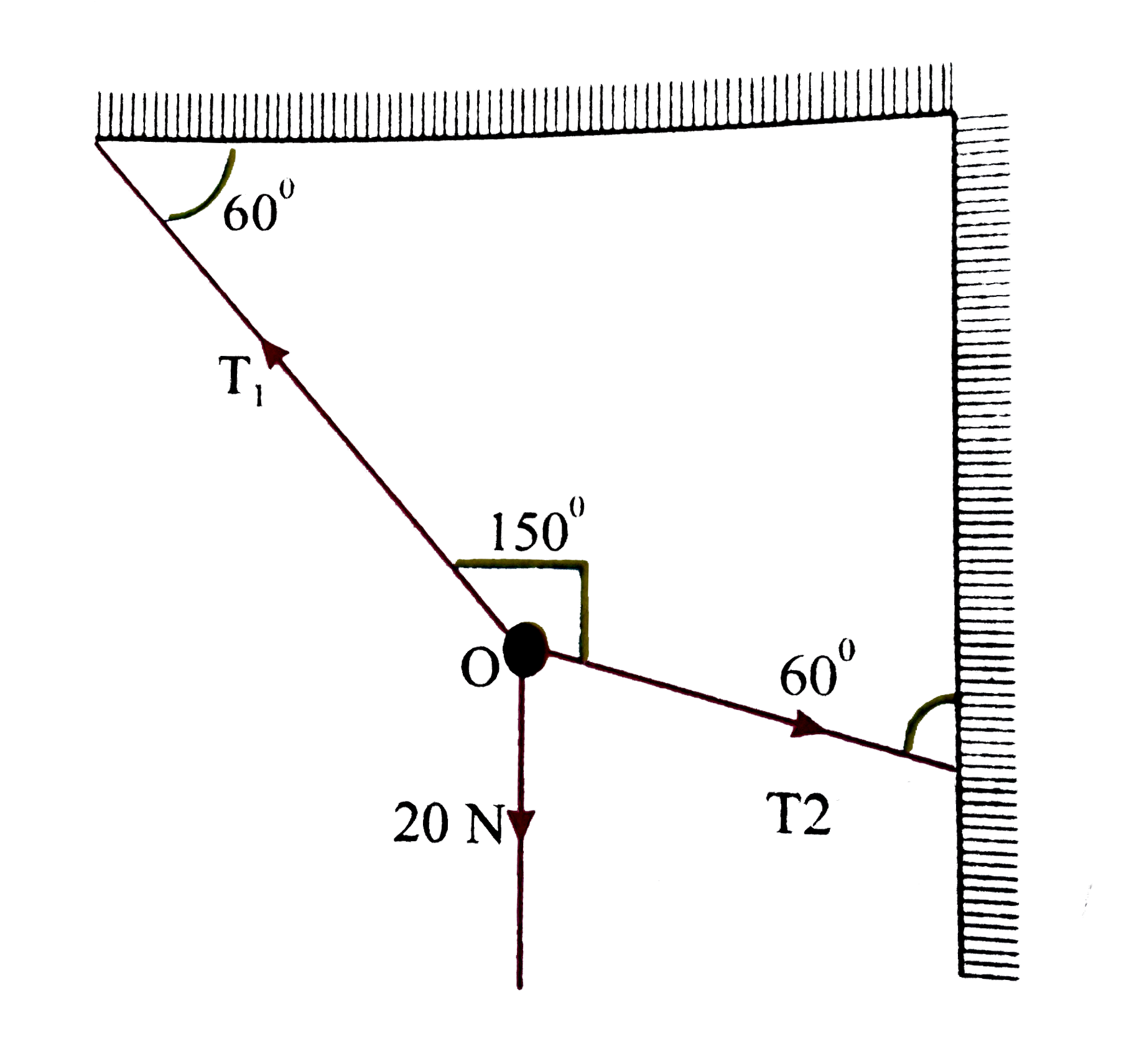
View SolutionA `1N` pendulum bob is held at an angle `theta` from the vertical by a `2N` horizontal force `F` as shown in figure. The The tension in the string supporting the pendulum bob (in newton) is
 .
.
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is `sqrt(0.44)` and the radius of the bowl is `0.6m`. The maximum height to which an insect can crawl in the bowl will be .
View SolutionA `500kg` horse pulls a cart of mass `1500kg` along a level road with an acceleration of `1m//s^(2)`. if coefficient of sliding friction is `0.2` then force exerted by the earth on horse is .
View SolutionAn aeroplane requires for take off a speed of `108` kmph the run on the ground being `100m` mass of the plane is `10^(4)kg` and the coefficinet of friction between the plane and the ground is `0.2`. Assuming the plane accelerates uniformly the minimum force required is `(g =10ms^(-2))` .
View SolutionA duster weighs `0.5N`. It is pressed against a vertical board with a horizontal force `11N` If the co-efficient of friction is `0.5` the mimmum force that must be applied on the duster parallel to the board to move it upwards is .
View SolutionA man of mass `65kg` is standing stationary with respect to a conveyor belt which is accelerating with `1m//s^(2)`. if `mu_(s)` is 0.2 the net force on the man and the maximum acceleration of the belt so that the man is stationary relative to the belt are `(g =10 m//s^(2))` .
View SolutionA man of mass `60kg` sitting on ice pushes a block of mass `12kg` on ice horizontally with a speed of `5ms^(-1)` The coefficient of friction between the man and ice and between block and ice is `0.2 If g =10ms^(2)` the distance beteen man and the block when they come to rest is .
View SolutionA vehicle of mass `M` is moving on a rough horizontal road with a momentum P If the coefficient of friction between the tyres and the road is `mu` is then the stopping distance is .
View SolutionThe rear side of a truck is open A box of `40kg` mass is placed `5m` away from the open end as shown in The coefficient of friction between the box and the surface is 0.15. On a straight road, the truck starts from rest and accel erating with `2m//s^(2)`. At what dis tance from the starting point does the box dis-tance from the starting point does the box fall from the truck? (Ignore the size of the box)
 .
.
View SolutionA block A of mass 3kg and another block `B` of mass `2kg` are connected by a light inextensible string as shown in figure. If the coefficient of friction between the surface of the table and A is 0.5 What maximum mass `C` is to be placed on A so that the system is to be in equlibrium
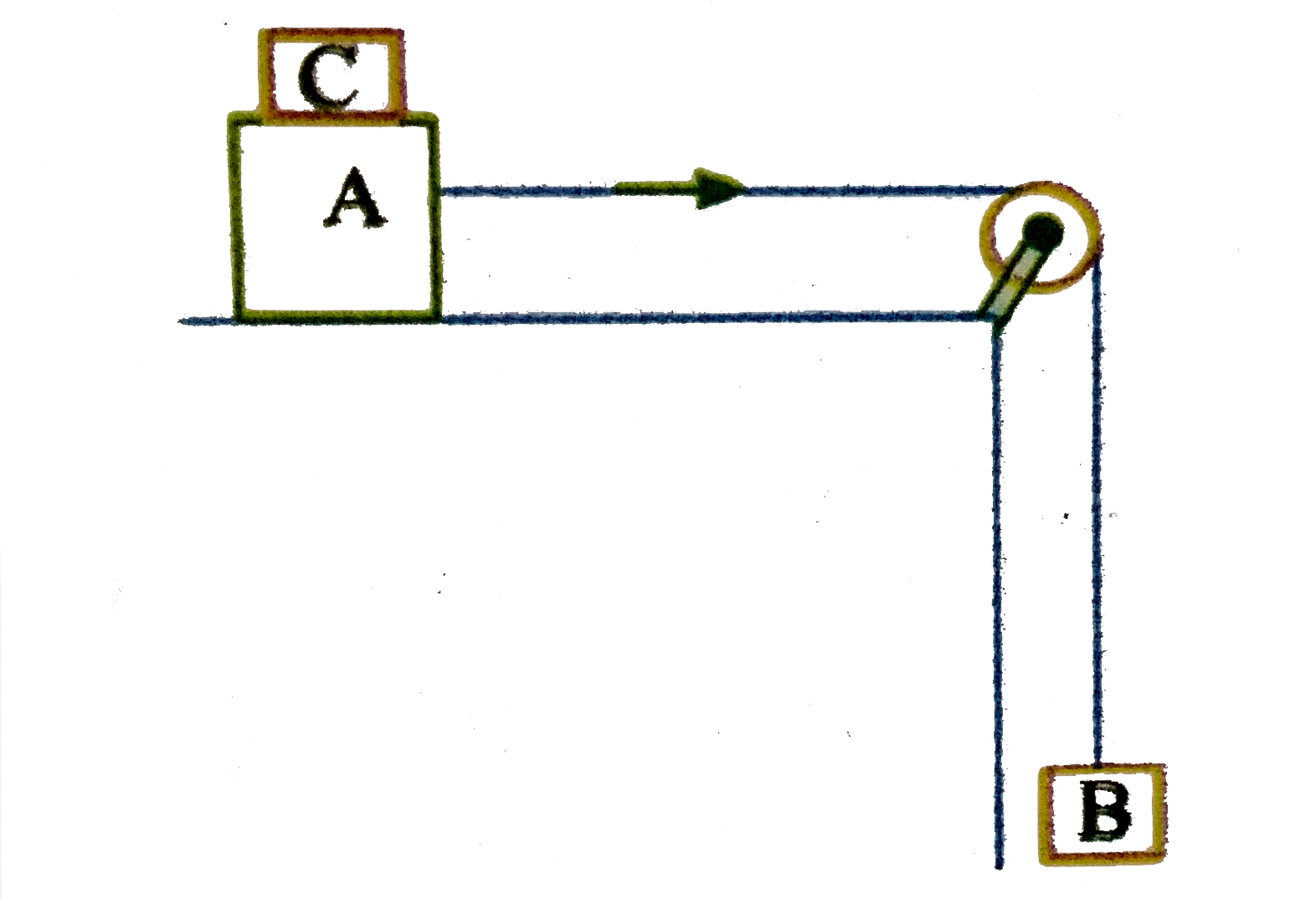 .
.
View SolutionA block slides down a rough inclined plane of slope angle `theta` with a constnat velocity. It is then projected up the same plane with an intial velocity v the distance travelled by the block up the plane coming to rest is .
View SolutionThe minimum force required to start pushing a body up rough (frictional coefficient `mu`) inclined plane is `F_(1)` while the minimum force needed to prevent it from sliding down is `F_(2)`. If the inclined plane makes an angle `theta` from the horizontal such that tan `theta=2mu` then the ratio `(F_1)/(F_2)` is
View SolutionThe horizontal acceleration that should be given to a smooth inclined plane of angle `sin^(-1)((1)/(l))` to keep an object stationary on the plane relative to the inclined plane is .
View SolutionA body is released from the top of a smooth inclined plane of inclination `theta`. It reaches the bottom with velocity `v`. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View SolutionThe force required to move a body up a rough inclined plane is double the force required to prevent the body from sliding down the plane. The coefficient of friction when the angle of inclination of the plane is `60^(@)` is .
View SolutionA smooth block is released at rest on a `45^(@)` incline and then slides a distance `d`. The time taken to slide is n times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
View SolutionThe upper half of an inclined plane with inclination `phi` is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionA `30kg` box has to move up an inclined plane of slope `30^(@)` the horizontal with a unform velocity of `5 ms^(-1)`. If the frictional force retarding the motion is `150N`, the horizontal force required to move the box up is `(g =ms^(-2))` .
View SolutionA block weighing `10kg` is at rest on a horizontal table. The coefficient of static friction between the block and the table is `0.5`. If a force acts downward at `60^(@)` with the horizontal, how large can it be without causing the block to move ? .`(g =100ms^(-2))` .
View SolutionPulling force making an angle `theta` to the horizontal is applied on a block of weight `W` placed on a horizontal table. If the angle of friction is `alpha`, then the magnitude of force is `alpha` , then the magnitude of force required to move the body is equal to
View SolutionA block of mass `sqrt3 kg` is kept on a frictional surface with `mu =(1)/(2sqrt3)`. The minimum force to be applied as shown the move the block is
 .
.
View SolutionA car is moving in a circular horizonta track of radius 10m with a constant speed of 10 m/s. A pendulum bob is suspended from the roof of the cat by a light rigid rod of length 1.00m. The angle made by the rod with track is
View SolutionA vehicle in moving with a velocity v on a carved total of width b and radius of curvature B For counteractiong the contritugal force on the vehicle , the difference in elevation required in between the outer and linner edges of the rod is

View SolutionThe centripetal force required for a `1000 kg` car travelling at `36kmph` to take a turn by `90^(@)` in travelling along an are of length `628 m` is .
View SolutionA small coin is placed on a flat horizontal turn table. The turn table is observed to make three revolutions in `3.14 sec`. What is the coefficient of static friction between the coin and turn table if the coin is observed to slide off the turn table when it is greater than `10cm` from the centre of turn table .
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Sch a system is called a conical pendulum.
View SolutionThree point masses each of mass m are joined together using a string to form an equilateral triangle of side a. The system is placed on a smooth horizontal surface and rotated with a constant angular velcoity `omega` about a vertical axis passing through the centroid Then the tension in each string is .
View SolutionA steel wire can withstand a load up to `2940N`. A load of `150 kg` is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load passs through the position of equilibrium, is
View SolutionA car is travelling along a curved road of radius r. If the coefficient of friction between the tyres and the road is `mu` the car will skid if its speed exceeds .
View SolutionA boy of mass `50kg` is standing on a weihing machine placed on the floor of a lift. The machine reads his weight in newtons. The reading of the machine if the lift is moving upwards with uniform speed of `10ms^(-1)` .
View Solution
LEVEL -II (C.W) questions and complete solutions for chapter NEWTONS LAWS OF MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11