Complete Solutions to C.U.Q of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| NARAYANA | C.U.Q |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
The concept of CM is applicable
View SolutionIf ecternal force acting on a system is constant . It means that the velocity of the CM .
View SolutionThe centre of mass of a body
View SolutionThe centre of mass of a system of particles does not depend on
View SolutionThe centre of mass of a body
View SolutionTwo bodies `A and B` initially at rest are attrached towards each other due to gravitation. Given that `A` is much heavier than `B`. Which of the followings correctly describes the relative motion of the centre of mass of the bodies ?
View SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View SolutionCentre of mass of the earth-moon system lies
View SolutionTwo balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
View SolutionFor a rotating body about fixed axis ,
View SolutionFor a pure rotational motion ,
View SolutionChoose the correct option for rotational motion .
View SolutionTwo particles `p` and `q` located at distances `r_p` and `r_q` respectively from the centre of a rotating disc such that `r_p gt r_q`.
View SolutionIdentify the increase in order of the angular velocities of the following
(A) earth rotating about its own axis
(b) hour's hand of a clock
(c) second's hand of a clock
(d) flywheel of radius 2 m making 300 rpm
View SolutionThe direction of following vectors is along the line of axis of rotation
View SolutionThe correct relation of the following is
View SolutionWhich of the following is wrong
View SolutionIf force vector is along X-axis and radius vector is along Y-axis then the direction of torque is
View SolutionDuring rotation of a body, the position vector is along X-axis and force vector is along Y-axis, The direction of torque vector is
View SolutionIf the direction of position vector `vec r` is towards south and direciton of force vector `vec F` is towards east, then the direction of torque vector `vec tau` is
View SolutionA circular disc is rotated along clockwise direction in horizontal plane. The direction of torque is
View SolutionMagnitude of torque is maximum in the following case
View SolutionA constant resultant torque rotates a wheel about its own axis. Then true statement of the following is
View SolutionA wheel is free to rotate about its own axis without friction. A rope is wound around the wheel. If other end of rope is pulled with a constant force, then true statement from the following is
View SolutionClass `I` lever is that in which
View SolutionThe example of a couple is
View SolutionThe example of lever is
View SolutionThen moment of inertia of a rigid body depends on
(A) mass of body
(B) position of axis of rotation
(C) time period of its rotation
(D) angular velocity of the body
View SolutionMoment of inertia of a body depends upon
View SolutionA brass disc is rotating about its axis. If temperature of disc is increased then its
View SolutionThe radius of gyration of a rotating metallic disc is independent of the following physical quantity.
View SolutionOne solid sphere `A` and another hollow sphere `B` are of same mass and same outer radii. Their moment of inertia about their diameters are respectively `I_(A)` and `I_(B)` such that.
View SolutionThe theorem of perpendicular axes is applicable for
View SolutionTheorem of parallel axes
View SolutionA boiled egg and a raw egg of same mass and size are made to rotate about their own axis. If `I_1` and `I_2` are moments of inertia of boiled egg and raw egg, then
View SolutionRaw and boiled eggs are made to spin on a smooth table by applying the same torque. The egg that spin faster is
View SolutionThe radius of gyration of a rotating circular ring is maximum about following axis of rotation
View SolutionA moment of inertia of a thin circular plate is minimum about the following axis
View SolutionA ring of mass `m` and radius `r` is melted and then moulded into a sphere. The moment of inertia of the sphere will be
View SolutionIdentify the correct order in which the ratio of radius of gyration to radius increases for the following bodies.
(I) rolling solid sphere
(II) rolling solid cylinder
(III) rolling hollow sphere
(IV) rolling hollow cylinder
View SolutionIdentify the increasing order of radius of gyration of following bodies of same radius
(I) About natural axis of circular ring
(II) about diameter of circular ring
(III) About diameter of circular plate
(IV) about diameter of solid sphere
View SolutionIdentify the decreasing order of radius of gyration of following bodies of same radius
(I) About diameter of circular ring
(II) About diameter of circular plate
(III) About tangent of circular ring `bot^(r)` to its plane
(IV) About tangent of circular plate in its plane
View SolutionThree dense point size bodies of same mass are attached at three vertices of a light equilateral triangular frame . Identify the increasing order of their moment of inertia about following axis .
I) About an axis `bot^(r )` to plane and passing through a corner
II) About an axis `bot^(r )` to plane passing through centre
III) About `bot^(r)` bisector of any side .
View SolutionFour point size dense bodies of same mass are attached at four corners of a light square frame . Identify the decreasing order of their moments of inertia about following axes .
I) Passing through any side
II) Passing through opposite corners III) `bot^(r)` bisector of any side
(IV) `bot^(r)` to the plane and passing through any corner
View SolutionA circular disc is rotating about its own axis, the direction of its angular momentum is
View SolutionAngular momentum of the particle rotating with a central force is constant due to
View SolutionA solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same which one of the following will not be affected?
View SolutionThe following motion is based on the law of conservation of angular momentum
(A) rotation of top (B) diving of driver
(C) rotation of ballet dancer on smooth horizontal surface
(D) a solid sphere that rolls down on an inclined plane
View SolutionThe law of conservation of angular momentum is obtained from Newton's II law in rotational motion when
View SolutionIf polar ice caps melt, then the time duration of one day
View SolutionIf most of the population on earth is migrated to poles of the earth then the duration of a day
View SolutionIf earth shrinks then the duration of day
View SolutionA ballet dancer is rotating about his own vertical axis on smooth horizontal floor. `I, omega, L, E` are moment of inertia, angular velocity, angular momentum, rotational kinetic energy of ballet dancer respectively. If ballet dancer stretches himself away from his axis of rotation, then
View SolutionA circular wheel is rotating in horizontal plane without friction about its axis. If a body is gently attached to the rim of the wheel then following is false.
View SolutionA ballet dancer is rotating at angular velocity `omega` on smooth horizontal floor. The ballet dancer folds his body close to his axis of rotation by which his radius of gyration decreases by `1//4^(th)` of his initial radius of gyration, his final angular velocity is
View SolutionIf a body is rolling on a surface without slipping such that its kinetic energy of translation is equal to kinetic energy of rotation then it is a
View SolutionIf a ring, disc, hollow sphere and solid sphere rolling horizontally without slipping with the same velocity on a surface, then translational kinetic energy is more for
View SolutionA ring, disc, hollow sphere and solid sphere roll on a horizontal surface with the same linear speed. If they have same mass and radius and move without slipping, rotational kinetic energy is more for
View SolutionIf `V` is velocity of centre of mass of a rolling body then velocity of lowest point of that body is
View SolutionIf the velocity of centre of mass of a rolling body is `V` then velocity of highest point of that body is
View SolutionA body is freely rolling down on an inclined plane whose angle of inclination is `theta`. If `a` is acceleration of its centre of mass then following is correct
View SolutionA sphere cannot roll on
View SolutionWhen the following bodies of same radius starts rolling down on same inclined plane, identify the decreasing order of their times of descent
(I) Solid cylinder , (II) hollow cylinder
(III) hollow sphere ,(IV) solid sphere
View SolutionWhen the following bodies having same radius starts rolling down on same inclined plane, identify the increasing order of their accelerations
(I) hollow cylinder ,(II) Solid cylinder
(III) solid sphere, (IV) hollow sphere
View SolutionWhen a ring is rolling and `V_1, V_2, V_3, V_4` are velocities of top most point, lowest point, end point of horizontal diameter, centre of ring respectively, the decreasing order of these velocities is
View SolutionThe increasing order of fraction of total kinetic energy associated with translatory motion of the following rolling bodies is
(I) circular ring ,(II) circular plate
(III) solid sphere ,(IV) hollow sphere
View SolutionP is a solid sphere and Q is a hollow sphere both having the same mass and radius .If they roll down from the top of an inclined plane , on reaching the bottom .
View SolutionA and B are two identical rings released from the top of an inclined plane . A slides down and B rolls down. Then which reaches the bottom first ?
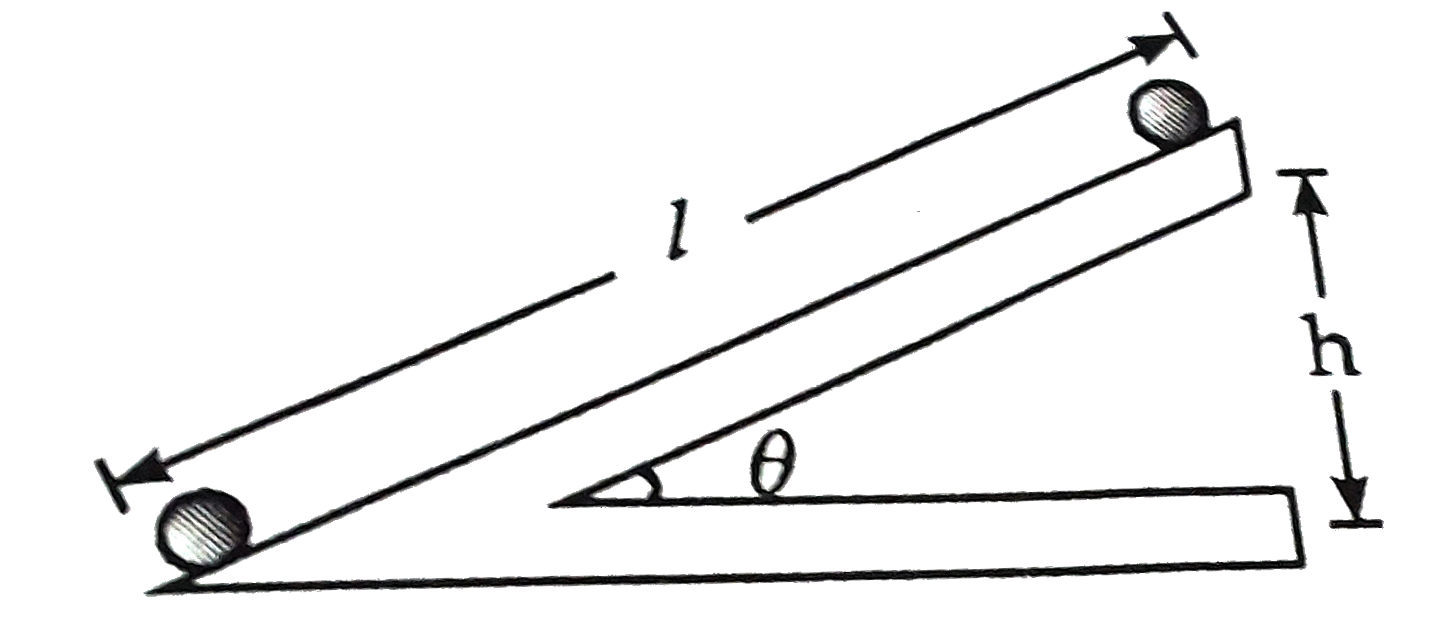
View SolutionIn the above problem , which will reach the bottom with greater velocity ?
View SolutionA ring, a disc a sphere and spherical shells are simutaneously released to roll down from the top of an inclined plane of height h. the four bodies will reach the bottom in the following order
View SolutionIn the above question , the reason for the bodies to have different times of descent is
View Solution
C.U.Q questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11