Complete Solutions to EXERCISE - II (C.W) of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| NARAYANA | EXERCISE - II (C.W) |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
A uniform wire is bent into the form of a rectangle of length `L` and width `W`. The coordinates of its centre of mass from a corner are
View SolutionA uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View SolutionIf three particles of masses `2kg, 1kg` and `3kg` are placed at corners of an equilateral triangle of perimeter `6m` then the distance of centre of mass which is at origin of particles from `1kg` mass is (approximately) (Assume `2kg` on x-axis)
View SolutionSix identical particles each of mass `m` are arranged at the corners of a regular hexagon of side length `L`. If the mass of one of the particle is doubled, the shift in the centre of mass is
View SolutionThree particles each of mass `2kg` are at the corners of an equilateral triangle of side `sqrt 3 m`. If one of the particles is removed, the shift in the centre of mass is
View SolutionA bomb of mass `m` at rest at the coordinate origin explodes into three equal pieces. At a certain instant one piece is on the x-axis at `x=40cm` and another is at `x=20cm, y=-60cm`. The position of the third piece is
View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure . The distance of centre of mass from D is

View SolutionThe centre of mass of the letter F which is cut from a unifrom metal sheet from point A is

View SolutionThe mass of a uniform ladder of length `5m` is `20kg`. A person of mass `60kg` stand on the ladder at a height of `2m` from the bottom. The position of centre of mass of the ladder and man from the bottom is
View SolutionFigure shows a square plate of unifrom thickness and side length `sqrt(2)` m . One fourth of the plate is removed as indicated . The distance of centre of mass of the remaining portion from the centre of the original square plate is

View SolutionA circular hole is radius 'r' is made in a disk of radius 'R' and of uniform thickness at a distance 'a' from the centre of disk . The distance of the new centre of mass from the original centre of mass is

View SolutionTwo particles of equal masses have velocities `vec(v)_(1)= 4hat(i) and vec(v)_(2) = 4 hat(j)` . First particle hac an acceleration of the other particle is zero . The centre of mass of the two particles moves in a path of
View SolutionA body of mass `m` is dropped and another body of mass `M` is projected vertically up with speed `u` simultaneously from the top of a tower of height `H`. If the body reaches the highest piont before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
View SolutionA rope thrown over a pulley has a ladder with a man of mass `m` on one of its ends and a counter balancing mass `M` on its other end. The man climbs with a velocity `v_r` relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionThe unit vector perpendicular to `vec A = 2 hat i + 3 hat j + hat k` and ` vec B = hat i - hat j + hat k` is
View SolutionAn electron is moving with speed `2xx10^5 m//s` along the positive x-direction in the presence of magnetic induction `vecB = (hat i + 4 hat j - 3 hat k) T`. The magnitude of the force experienced by the electron in `N ( e = 1.6xx 10^(-19) C) ( vec F = q ( vec v xx vec B))`
View SolutionThe linear and angular velocities of a body in rotatory motion are `3 ms^(-1)` and `6 rad//s` respectively. If the linear acceleration is `6 m//s^2` then its angular acceleration in `rad s^(-2)` is
View SolutionA stationary wheel starts rotating about its own axis at an angular acceleration `5.5 rad//s^(2)` . To acquire an angular velocity 420 revolutions per minute , the number of rotations made by the wheel is
View SolutionA circular disc is rotating about its own axis at a uniform angular velocity `omega`. The disc is subjected to uniform angular retardation by which its angular velocity is decreased to `omega/2` during `120` rotations. The number of rotations further made by it before coming to rest is
View SolutionA wheel starting from rest is uniformly accelerate at `4rad/s^2` for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
View SolutionTwo points P and Q ,diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc .

View SolutionA shaft is turning at `65rad//s` at time zero. Thereafter, angular acceleration is given by `alpha=-10rad//s^(2)-5trad//s^(2)`
Where `t` is the elapsed time
(a). Find its angular speed at `t=3.0` s
(b). How much angle does it turn in these `3s`?
View SolutionAverage torque on a projectile of mass `m` (initial speed `u` and angle of projection `theta`) between initial and final positions `P` and `Q` as shown in figure, about the point of projection is :
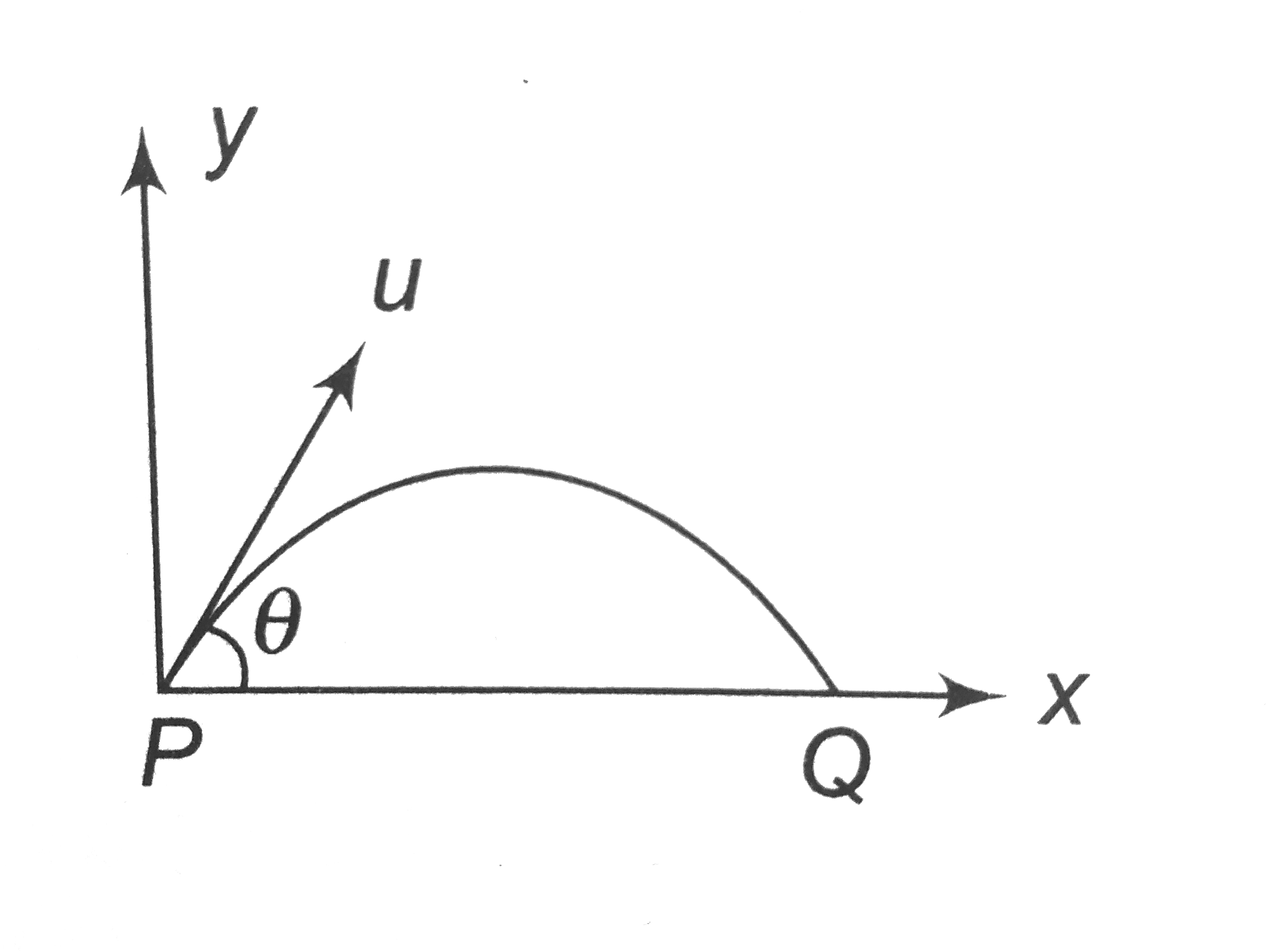 .
.
View SolutionA metal rod of uniform thickness and of length `1m` is suspended at its `25cm` division with help of a string. The rod remains horizontally straight when a block of mass `2kg` is suspended to the rod at its `10cm` division. The mass of rod is
View SolutionA roller of mass `300kg` and of radius `50cm` lying on horizontal floor is resting against a step of height `20cm`. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
View SolutionTwo persons `P` and `Q` of same height are carrying a uniform beam of length `3m`. If `Q` is at end, the distane of `P` from the other end so that `P,Q` receive loads in the ratio `5:3` is
View SolutionA metallic cube of side length `1.5m` and of mass `3.2` metric ton is on horizontal rough floor. The minimum horizontal force that should be applied on the cube at a height `1.2m` from that floor to turn the cube about its lower edge is
View SolutionTwo identical circular plates each of mass `0.1` kg and radius 10 cm are joined side by side as shown in the figure . Their moment of inertia about a axis passing through their common tangent is

View SolutionA thin rod of mass `M` and length `L` is bent into a circular ring. The expression for moment of inertia of ring about an axis passing through its diameter is
View SolutionMoment of inertia of a thin circular plate of mass `M`, radius `R` about an axis passing through its diameter is `I`. The moment of inertia of a circular ring of mass `M`, radius `R` about an axis perpendicular to its plane and passing through its centre is
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length 2R as shown in the figure the . The moment of inertia of the system about an axis passing through the centre of one of the spheres and perpendicular to the rod is

View SolutionThe ratio of radii of two solid spheres of same material is `1:2`. The ratio of moments of inertia of smaller and larger spheres about axes passing through their centres is
View Solution`I` is moment of inertia of a thin circular ring about an axis perpendicular to the plane of ring and passing through its centre. The same ring is folded into `2` turns coil. The moment of inertia of circular coil about an axis perpendicular to the plane of coil and passing through its centre is
View SolutionThe moment f inertia of a solid cylinder about an axis parallel to its length and passing through its centre is equal to its moment of inertia about an axis perpendicular to the length of cylinder and passing through its centre . The ratio of radius of cylinder and its length is
View SolutionThe radius of gyration of rod of length `L` and mass `M` about an axis perpendicular to its length and passing through a point at a distance `L//3` from one of its ends is
View SolutionThree rings each of mass M and radius R are arranged as shown in the figure . The moment of inertia of the system about AB is
`(NAR_NEET_PHY_XI_P2_C07_E11_036_Q01.png" width="80%">
View SolutionTwo point size bodies of masses `2kg, 3kg` are fixed at two ends of a light rod of length `1m`. The moment of inertia of two bodies about an axis perpendicular to the length of rod and passing through centre of mass of two bodies is
View Solution`I` is moment of inertia of a thin circular plate about its natural axis. The moment of inertia of a circular ring whose mass is half of mass of plate but radius is twice the radius of plate about an axis passing through any tangent of ring in its plane is
View SolutionThree indentical thin rods each of mass m and length L are joined together to form an equilateral triangular frame . The moment of inertia of frame about an axis perpendicular to the palne of frame and apssing through a corner is
View SolutionFour spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionThe moment of inertia of a hollow sphere of mass `M` having internal and external radii `R` and `2R` about an axis passing through its centre and perpendicular to its plane is
View SolutionThickness of a wooden circular plate is same as the thickness of a metal circular plate but density of metal plate is `8` times density of wooden plate. If moment of inertia of wooden plate is twice the moment of inertia of metal plate about their natural axes, then the ratio of radii of wooden plate to metal plate is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to the plane at an angular velocity `omega ` . Another disc of mass M / 3 but same radius is placed gently on the first disc coaxially . the angular velocity of the system now is
View SolutionA turn table is rotating in horizontal plane about its own axis at an angular velocity 90 rpm while a person is on the turn table at its edge. If he gently walks to the centre of table by which moment of inertia of system decreases by `25%`, then the time period of rotating of turn table is
View SolutionA uniform cylindrical rod of mass m and length L is rotating is perpendicular to its axis of symmetry and passes through one of its edg faces . If the room temperature increases by 't' and the coeffcient of linear expansion is `alpha `, th change in its angular velocity is
View SolutionA particle of mass `1 kg` is moving alogn the line `y=x+2` with speed `2m//sec`. The magnitude of angular momentum of the particle about the origin is
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible sixe , each has two identical beads of negligible size , each of mass m , which can slide freely along the rod . Intially the two beads are at athe centre of the rod and the system is rotating with angular velocity `omega_(0)` about its axis perpendicular to the rod passing trough its mid point ( see figure ) . There are no through its mid point ( see figure ) . There are no external forces . When the beads reach the ends of the rod , the angular velocity of the system is

View SolutionAn energy of `484 J` is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Calculate moment of inertia of flywheel.
View SolutionA constant torque of `1000 N-m` turns a wheel of moment of inertia `200 kg-m^2` about an axis through its centre. Its angular velocity after `3` seconds is.
View SolutionIf the angular momentum of a rotating body about an axis is increased by 10%. Its kinetic energy increases by
View SolutionThe angular frequency of a fan of moment of inertia `0.1kgm^2` is increased from 30rpm to 60rpm when a torque of `0.03Nm` acts on it. The number of revolutions made by the fan while the angular frequency is increased from 30rpm to 60rpm
View SolutionA sphere of mass `m` and radius `r` rolls on a horizontal plane without slipping with a speed `u`. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionA circular ring starts rolling down on an inclined plane from its top. Let `v` be velocity of its centre of mass on reaching the bottom of inclined plane. If a block starts sliding down on an identical inclined plane but smooth, from its top, then the velocity of block on reaching the bottom of inclined plane is
View SolutionA thin rod of length `L` is vertically straight on horizontal floor. This rod falls freely to one side without slipping of its bottom. The linear velocity of centre of rod when its top end touches floor is
View SolutionA wheel of radius 'r' rolls without slipping with a speed v on a horizontally road . When it is at a point A on the road , a small lump of mud separates from the wheel at its highest point B and drops at point C on the ground . The distance AC is

View SolutionA solid cylinder of mass `m` rolls without slipping down an inclined plane making an angle `theta` with the horizontal. The frictional force between the cylinder and the incline is
View SolutionA metal disc of radius `R` and mass `M` freely rolls down from the top of an inclined plane of height `h` without slipping. The speed of its centre of mass on reaching the bottom of the inclined plane is
View SolutionA hollow sphere rolls on a horozontal surface without slipping. Then percentages of rotational kinetic energy in total energy is
View SolutionA disc is rolling the velocity of its centre of mass is `V_"cm"` then which one will be correct : -
View SolutionA tangential force F acts at the top of a thin spherical shell of mass m and radius R . Find the acceleration of the shell if it rolls without slipping

View Solution
EXERCISE - II (C.W) questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11