Complete Solutions to Illustration of chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| NARAYANA | Illustration |
| Number Of Questions | 93 |
| Academic Year | 2023-24 |
Two particles of masses 1kg and 2kg are located at `x=0` and `x=3m`. Find the position of their centre of mass.
View SolutionWhen `'n'` number of particles of masses `m, 2m, 3m,….nm` are at distances `x_1 =1, x_2 =2, x_3=3…x_n = n` units respectively from origin on the X-axis, then find the distance of centre of mass of the system from origin.
View SolutionWhen `'n'` number of particles of masses `m, 2m, 3m,….nm` are at distances `x_1 =1, x_2 =4, x_3=9…x_n = n^2` units respectively from origin on the X-axis, then find the distance of centre of mass of the system from origin.
View SolutionWhen `'n'` number of particles of masses `m` are at distances `x_1 =a, x_2 =ar, x_3=ar^2…x_n = ar^n` ,units from origin on the X-axis, then find the distance of centre of mass of the system from origin.
View SolutionThe position vectors of three particles of mass `m_(1) = 1kg, m_(2) = 2kg and m_(3) = 3kg` are `r_(1) = ((hat(i) + 4hat(j) +hat(k))`m, `r_(2) = ((hat(i)+(hat(j)+hat(k))`m and `r_(3) = (2hat(i) - (hat(j) -(hat(2k))`m, respectively. Find the position vector of their center of mass.
View SolutionThree particles of masses `0.50 `kg , 1.0 kg and 1.5 kg are placed at the three corners of right - angles triangle of sides 3.0 cm , 4.0 cm and 5.0 cm as shown in figure . Locate the centre of mass of the system .

View Solution
Four particles of masses 1 kg , 2 kg , 3 kg and 4 kg are placed at the four vertices A,B,C and D of the square of side 1 m as shown in figure . Find the position of centre of mass of the particles .
View SolutionFind position of centre of mass of four particle system , which are at the vertices of a parallelogram , as shown in figure .

View SolutionIf the centre of mass of three particles of masses of `1kg, 2kg, 3kg` is at `(2,2,2)`, then where should a fourth particle of mass `4kg` be placed so that the combined centre of mass may be at `(0,0,0).`
View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionFind the coordination of the centre of mass of a uniform semicircular wire of radius R and mass M.
View SolutionIf the linear density of a rod of length L varies as `lambda = A+Bx` , find the position of its centre of mass .
View SolutionFind the distance of centre of mass of a uniform cone of height 'h' and base radius R, from the vertex on the line of symmetry .
View SolutionFind the centre of mass of a uniform L shaped lamina ( a thin flat palte ) with dimensions as shown . The mass of the lamina is 3 kg .

View SolutionThe objects in the figure are constructed of uniform wire bent into the shape shown . Find the position of the centre of mass of each shape from the point 'O'

View SolutionTwo blocks A and B of equal masses are released on two sides of a fixed wedge C as shown in figure .. Find the acceleration of centre of mass of blocks A and B . Neglect friction .

View SolutionTwo particles A and B of masses 1 kg and 2 kg respectively are projected in the directions shown in figure with speed `u_(A) = 200` m/s and `u_(B) = 50 ` m/s . Initially they were 90 m apart . Find the maximum height attained by the centre of mass of the particles . Take `g = 10m//s^(2)`

View SolutionIn the arrangement shown in the figure , A has mass `m_(1) = 3kg ` and B has mass `m_(2) = 5` kg and the string is light and inextensible . Find the acceleration of centre of mass of this pair of blocks . Neglect friction everywhere

View SolutionA `10 kg` boy standing in a `40 kg` boat floating on water is `20 m` away from the shore of the river. If the boy moves `8 m` on the boat towards the shore, then how far is he from the shore ? (Assume no friction between boat and water).
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance aR from the centre of the bigger disc. The value of a is
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure . Find the displacement of wedge on the horizontal ground when the block reaches the bottom of the wedge . Neglect friction everywhere

View SolutionA truck of mass `2xx10^3kg` travelling at `4m//s` is brought to rest in `2s` when it strikes a wall. What force (assume constant) is exerted by the wall?
View SolutionConsider a two particle system with particles having masses `m_1 and m_2` if the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle is moved, so as to keep the center of mass at the same position?
View SolutionTwo blocks of equal mass m are connected by an unstreched spring and the system is kept at rest on a frictionless horizontal surface . A constant force F is applied on one of the blocks pulling it away from the other as shown in figure .

(a) Find the position of the centre of mass at time t .
(b) If the extension of the spring is `x_(0)` at time t , find the displacement of the two blocks at this instant .
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure . All the surfaces are frictionless. The system is released from rest. Find the distance moved by the bigger block at the instant the smaller block reaches the ground.
 .
.
View SolutionA disc starts rotating with constant angular acceleration of `pi ("rad")/s^(2)` about a fixed axis perpendicular to its plane and through its centre .
(a) Find the angular velocity of the disc after 4s .
(b) Find the angular displacement of the disc after 4 s and
(c ) Find number d of turns accomplished by the disc in 4 s .
View SolutionThe motor of an engine is erotating about its axis with an angular velocity of 100 rev/minute. It comes to rest in 15 s, after being switched off. Assumgn cnstant angular decelertion, calculate the number of revolutions made by it before coming to rest.
View SolutionA wheel is mounted on a stationary axle starts from rest and is given by the following angular acceleration : ` alpha = 9 - 12 t ` (in SI unit ) where t is the time after the wheel begins to rotate . Find the number of revolutions that the wheel turns before it stops ( and begins to turn in the opposite direction ) .
View SolutionA wheel rotates with an angular acceleration given by `alpha =4at^3 - 3 bt^2`, where `t` is the time and `a` and `b` are constants. If the wheel has initial angular speed `omega_0`, write the equations for the (a) angular speed (b) angular displacement.
View SolutionA flywheel of radius 30 cm starts from rest and accelerates with constant with constant angular acceleration 0.5 `rad//s^(2)` . Compute the tangential , radial and resultant accelerations of a point on its circumference :
(a) initially at `theta = 0^(@)`
(b) after it has made one thrid of a revolution
View SolutionA flywheel rotates with a uniform angular acceleration. Its angular velocity increases from `20pi rad//s` to `40pi rad //s` in 10 seconds. How many rotations did it make in this period ?
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle `theta` with x-axis.
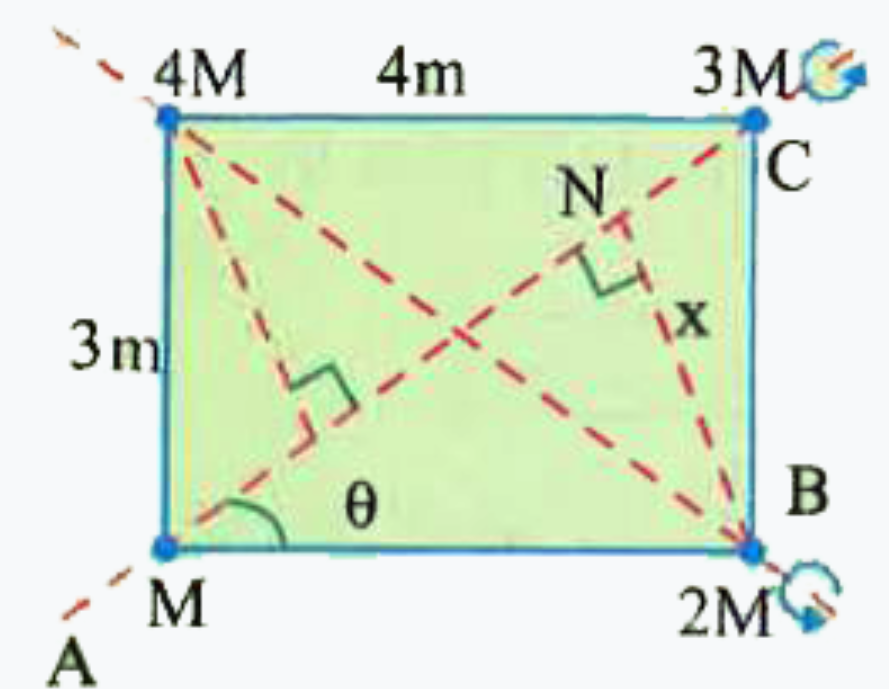
View SolutionFour point masses lie at the corners of a rectangle with sides of length 3 m and 4 m ., as shown in figure . Find the moment of inertia about of the diagonals . Take M = 1 kg .
View SolutionTwo masses `m_(1) and m_(2)` are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionThree particles , each of mass m , are situated at the vertices of an equilateral triangle . Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC .

View SolutionFour particles each of mass m are kept at the four corners of a square of edge a . Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the centre of the square .

View SolutionThe radius of gyration of a body about an axis at a distance of `12cm` from its centre of mass is `13cm`. Find its radius of gyration about a parallel axis through its centre of mass.
View SolutionFind the moment of inertia = of a thin rod of mass M and length L about an axis at one end and perpendicular to the rod ,as shown in figure

View SolutionA rod PQ of mass 'm' and length L is rotated about an axis through 'P ' as shown in figure. Find the moment of inertia of the rod about the axis of rotation .

View SolutionFind the moment of inertia of a circular disc or solid cylinder of radius R about the following axes .
(a) passing through the centre and perpendicular to the flat surface .
(b) at the rim and perpendicular to the flat surface
View SolutionFind the moment of inertia of a thin uniform rod about an axis perpendicular to its length and passing through a point which is at a distance of `1/3` from one end. Also find radius of gyration about that axis.
View SolutionTwo identical rods each of mass M and length L are joined in cross position as shown in figure . The moment of inertia of a system about a bisector would be .

View SolutionFour thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View SolutionTo discs have same moment of inertia about their own axes . Their thickness are also same . If the ratio of their material densities is 16 :1 . Find the ratio of their radii .
View SolutionThe moment of inertia of a disc, of mass M and radius R, about an axis which is a tangent and parallel to its diameter is
View SolutionFour spheres each diameter 2a and mass 'm' are placed with their centres on the four corners of a square of the side b. Calculate the moment of inertia of the system about any side of the square.
View SolutionFind Moment of inertia of an annular disc of mass M and internal and external radii `R_(1) and R_(2)` respectively .

View SolutionFind moment of inertia of a sector of mass M , radius R and of central angle `theta` radians .
View SolutionFind moment of inertia of a sector cut from a disc of mass M, radius R and central angle `theta `
View SolutionProve that moment of inertia of an angular sphere about its diameter . ( Given mass , internal and external radii are M , `R_(1) and R_(2)` respectively ) is
`I = 2/5 M ((R_(2)^(5)-R_(1)^(5))/(R_(2)^(3)-R_(1)^(3)))`
View SolutionA uniform wire of length l and mass M bented in The shape of semicircle of radius r as shown in figure . Find the moment of inertia about XX

View SolutionFour holes of radius R are cut form a thin square plate of the side 4R and mass M in xy plane shown . Then moment of inertia of the rmaining portion about z - axis is

View SolutionA uniform rod of mass 20 kg is hanging in in horizontal position with the help of two threads . It also supports a 40 kg mass as shown in the figure . Find the tension developed in each thread .

View SolutionA particle is projected at time `t=0` from a point `O` with a speed `u` at an angle `theta` to horizontal. Find the torque of a gravitational force on projectile about the origin at time `t. (x,y` plane is vertical plane)
View SolutionForce `2hat(i) +7hat(j) , 2hat(i) +5hat(j)+7hat(k) and hat(i) -2hat(j) +hat(k)` act at `(4,-1,2)` . Find the net torque of these forces about `(6,1,-3)`
View SolutionFind the net torque of these following forces about origin `vec(F)_(1) = hat(i) - hat(j) ` acting at ` vec(r_(1))= 2hat(i) + hat(j), vec(F)_(2) = -hat(i) + hat(j)` acting at `vec(r_(2)) =hat(i) +2hat(j) & vec(F)_(3) = hat(i) +hat(j) `acting at `vec(r )_(3) = hat(i) - hat(j)` .
View SolutionFind `alpha and beta ` if the force `vec(F) = 2hat(i) - 3hat(j) +hat(k)` acting at `(2,beta,-1)` produces no torque about `(alpha,0,2)`
View SolutionFind the moment of the couple formed by forces `5hat(i) +hat(k)` acting at `(9,-1,2) and -5hat(i)-hat(k) ` acting at `(3,-2,1)`
View SolutionOn a disc of mass 10 kg and diameter 40 cm , few forces are acting as shown in diagram . Find the torque acting and initial angular accceleration `alpha` of the disc .

View SolutionOn a triangular sheet pivoted at O , several forces are acting as shown in diagram . Find torque about O on the triangular sheet

View SolutionThe disc of mass MM is pivoted at P . If it is released from the position shown . Find its initial angular acceleration . The disc is in a vertical plane .

View SolutionA rod is kept orizontally on the two supports as shown in diagram . The mass of the rod is M and its length is L . Find the normal reactions on the two supports due to the rod is M and its length is L . Find the normal reactions on the two supports due to the rod

View SolutionA uniform cube of side a and mass `m` rests on a rough horizontal table. A horizontal force `F` is applied normal to one of the faces at a point directly above the centre of the face, at a height `(3a)/(4)` above the base. What is the minimum value of `F` for which the cube begins to tip about an edge?
View SolutionA spool (cylinder) rotating about its axis and a mass 'm' tied it which falls as string is unwinded . Find the acceleration of the mass m and tension in the string

View SolutionA griding stone in the form of a solid cylinder has a radius of 0.5 m and a mass 50 kg . Find
What torque will bring it from rest to an angular velocity of 300 rev/min in 10 s ?
(b) What is the kinetic energy when it is rotating at 300 rev/min ?
View SolutionCalculate the torque developed by ann airplane engine whose output is `2000 HP` at an angular velocity of `2400 rev//min`.
View SolutionA disc -shaped pulley has mass M = 4 kg and radius R = 0.5 m . It rotates freely on a horizontal axis , as in fig . A block of mass m = 2 kg hangs by a string that is tightly wrapped around the pulley .
(a) What is the angular velocity of the pulley 3s after the block released ?
(b) Find the speed of the after it has fallen 1.6 m .
Assume the system starts at rest .

View SolutionFor the arrangement shown on the figure , the string is tightly wrapped over the pilley . Find the acceleration of each block when released from rest . The string is not slipping over the pulley .

View SolutionA uniform rod of length L and mass M is pivoted freely at one end .
(a) What is the angular acceleration of the rod when it is at angle `theta ` to the vertical
What is the tangential linear acceleration of the free end when the rod is horizontal ?

View SolutionA solid cyclinder of mass m = 4g and radius R = 10 cm has ropes wrapped around it , one near each end . The cylinder is held horizontally by fixing the two free ends of the cords are exactly vertical ..The cylinder is released to fall under gravity . Find the tension in the cords whenn they unwind and the linear acceleration of the cylinder .

View SolutionA wheel of radius 10 cm cm can rotate freely about its centre as shown o in figure . A string is wrapped over its rim and is pulled by a force of 5.0 N . It is found that the torque produces an angular accceleration of 2.0 ` "rad/s"^(2)` in the wheel . Calculate the moment of inertia of the wheel .

View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure . A string is wrapped over its rim and a block of mass m attached to the free end of the string . The system is released from rest . Find the speed of the block as it descends through a height h .

View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 `kg-m^2` nd radius 20 cm. The wheel is free to rotate about it axis. Initially, thewheel is t rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA particle of mass 0.01 kg having position vector `vecr = ( 10 hati + 6 hatj)` meters is moving with a velocity `5 hati `m/s . Calculate its angular momentum about the origin.
View SolutionA uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is

View SolutionA ballet dancer spins about a vertical axis at `60 "rpm"` with arms outstretched. When her arms are folded the angular frequency increases to `90 "rpm"`. Find the change in her moment of inertia.
View SolutionA uniform rod `AB` of mass `m` length `2a` is allowed to fall under gravity with `AB` in horizontal. When the speed of the rod is `v` suddenly the end `A` is fixed. Find the angular velocity with which it begins to rotate.
View SolutionA turntable turns about a fixed vertical axis, making one revolution in `10 s`. The moment of inertia of the turntable about the axis is `1200 kgm^(2)`. A man of `80 kg`, initially standing at centre of the turnable, runs out along the radius. What is the angular velocity of the turtable when the man is `2 m` from the centre?
View SolutionA cockroach is moving with velocity `v` in anticlockwise direction on the rim of a disc of radius `R` of mass `m`. The moment of inertia of the disc about the axis is `I` and it is rotating in clockwise direction with an angular velocity `omega`. If the cockroach stops, the angular velocity of the disc will be
View SolutionA small block of mass 4 kg is attached to a cord passing through a hole in a horizontal frictionless syurface . The block is originally revolving in a circle of radius 0.5 m about the hole , with a tangential velocity of 4 m/s . The cord is then pulled slowly from below , shortening the radius of the circle in which the block revolves . The breaking strength of the cord is 600 N . What will be the radius of the circle when the cord breaks ?
View SolutionA uniform bar of length 6a and mass 8 m lies on a smooth horizontal table . Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively strike the bar (as shown in fig) and stick to the bar after collision Calculate
(a) velocity of the centre of mass
(b) angular velocity about centre of mass and
(c ) total kinetic energy , just after collision .

View SolutionA motor rotates a pulley of radius `25cm` at 20rpm. A rope around the pulley lifts a `50kg` block, What is the power output of the motor?
View SolutionTwo small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed `omega`. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionA uniform rod of mas m and length l is kept vertical with the lower end clamed. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest positon. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?
View SolutionA rogid body of radius of gyration k and inclined plane at an angle `theta ` with horizontal . Calculate its acceleration and the frictional force acting on it . Also find the expressions for velocity as it reaches the lowest point and the time taken to reach the lowest point .
View SolutionA uniform sphere of mass 200 g rols withiout slipping on a plane surface so that its centre mioves at a speed of 2.00 cm/s. Find its kinetic energy.
View SolutionA solid sphere rolls without slipping down a `30^(@)` inclined plane. If `g=10 ms^(-2)` then the acceleration of the rolling sphere is
View SolutionA wheel of bicycle is rolling without slipping on a level road . The velocity of the centre of mass is vCM , then the velocity of point A is

View SolutionA uniform solid sphere rolls on a horizontal surface at `20 ms^(-1)` . It then rolls up in incline having an angle of inclination at `30^(@)` with the horizontal . If the friction losses are negligible , the value of height h above the ground where the ball stops is
View SolutionA solid sphere rolls down an inclined plane and its velocity at the bottom is `v_(1)` .The same sphere slides down the plane (without friction ) and its velocity at the bottom is `v_(2)` . Find the relation between `v_(1) & v_(2)`
View SolutionA disc is rolling (without slipping) on a frictionless surface . C is its centre and Q nd p are two points equidistant from C . Velocities of points P,Q and C respectively , then

View SolutionA solid cylinder rolls down an inclined plane of height `h` and inclination `theta`. Calculate its speed to the bottom of the plane using acceleration method and energy method. Also calculate the time taken to reach of the bottom.
View Solution
Illustration questions and complete solutions for chapter SYSTEM OF PARTICLES AND ROTATIONAL MOTION of NARAYANA PHYSICS (HINGLISH) of Class 11