Complete Solutions to Examples of chapter MECHANICAL PROPERTIES OF FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| NARAYANA | Examples |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
The pressure at the bottom of a lake due to water is `4.9xx 10^(6)N//m^(2)`. What is the depth of the lake?
View SolutionWhat is force on the base of a tank of base area `1.5m^(2)` when it is filled with water upto a height of 1m
`(rho_("water")=10^(3)kg//m^(3),P_(0)=10^(5)Pa` and `g=10m//s^(2))`
View SolutionWhen equal volumes of two metals are mixed together the specific gravity of alloy is 4. When equal masses of the same two metals are mixed together the specific gravity of the alloy not becomes 3. find specific gravity of each metal?
(specific gravity `=("density of substance")/("density of water"))`
View SolutionWhen a polar bear jumps on an iceberg, its weight 240 kg.wt is just sufficient to sink the iceberg. What is the mass of the iceberg? (specific gravity of ice is 0.9 and that of sea water is 1.02)
View SolutionFour-fifths of a cylindrical block of wood, floats in a liquid. Assuming the relative density of wood be 0.8 find the density of the liquid.
View SolutionTwo bodies are in equilibrium when suspended in water from the arms of a balance.The mass of one body is `28 g` and its density is `5.66 g//cm^3`. If the mass of the other body is `36 g`, what is its density ?
View SolutionA certain block weighs 15 N in air. But is weighs only 12 N when completely immersed in water. When immersed completely in another liquid, it weighs 13 N. Calculate the relative density of (i) the block and (ii) the liquid.
View Solution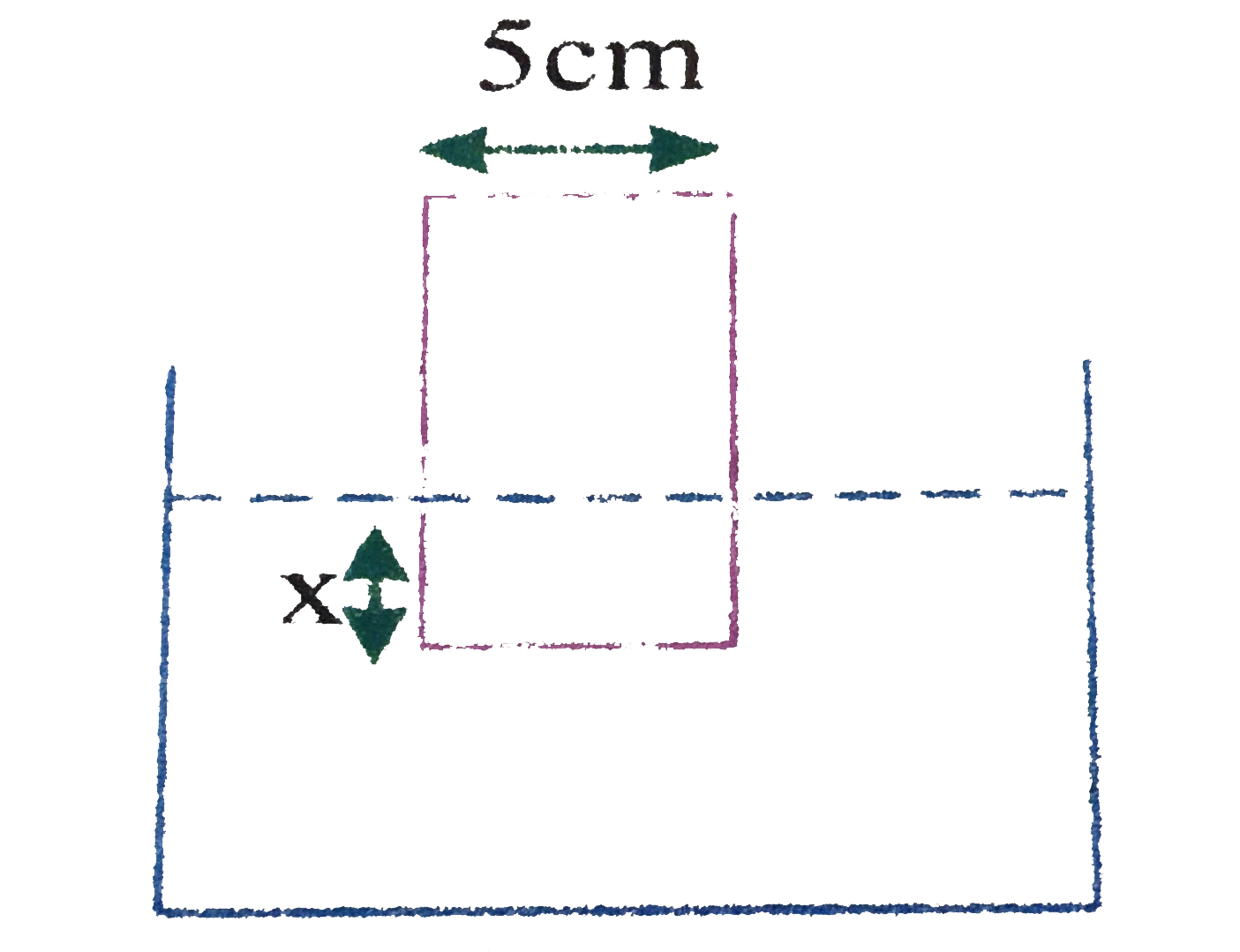
A cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level.
`(rho_(Hg)=13.6g//cm^(3),rho_(Fe)=7.2g//cm^(3))`
View SolutionA solid sphere of radius `R` has a concentric cavity of radius `(R)/(3)` inside it. The sphere is found to just float in water with the highest point of it touching the water surface. Find the specific gravity of the material of the sphere.
View SolutionA ball of relative density 0.8 falls into water from a height of 2 m. find the depth to which the ball will sink (neglect viscous forces)
View SolutionA small ball of density `rho` is immersed in a liquid of density `sigma(gtrho)` to a depth `h` and released. The height above the surface of water up to which the ball will jump is
View SolutionTwo spheres of volume 250 cc each but of relative densities 0.8 an d 1.2 are connected by a string and the combination is immersed in a liquid. Find the tension I the string. `(g=10m//s^(2))`
View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density `sigma` at equilibrium position. The extension `x_0` of the spring when it is in equlibrium is:
View SolutionA block is fully submerged in a vessel filled with water by a spring attached to the bottom of the vessel. In equilibrium position spring is compressed. If the vessel now moves downwards with an acceleration `a(lt g)`. What happens to the length of the spring.?

View SolutionWhat are the dimensions of Reynolds number ?
View SolutionWhat should be the average velocity of water in a tube of diameter 2 cm so that the flow is (i) laminar (ii) turbulent? The viscosity of water is 0.001 Pa-s. (for water pipes `Rlt 2000` stream line flow, `Rgt3000` turbulent flow)
View SolutionA siphon tube is used to remove liquid from a container as shown in fig. In order to operate the siphon tube, it must initially be filled with the liquid.
(i). Determine the pseed of the liquid through the siphon.
(ii). Determine the pressure at the point C.

View SolutionA pipe having an internal diameter D is connected to another pipe of same size. Water flows into the second pipe through n holes, each of diameter d. if the water in the first pipe has speed v, the speed of water leaving the second pipe is
View SolutionA syringe of diameter 1 cm having a nozzle of diameter 1 mm is placed horizontally at a height 5 m from the ground an incompressible non-viscous liquid is filled in the syringe and the liquid is compressed by moving the piston at a speed of `0.5ms^(-1)` the horizontal distance travelled by the liquid jet is `(g=10ms^(-2))`
View SolutionAir is streaming past a horizontal air plane wing such that its speed is `120 ms^-1` over the upper surface and `90 ms^-1` at the lower surface. If the density of air is `1.3 kg m^-3`m find the difference in pressure between the top and bottom of the wing. If the wing is `10 m` long and has an average width of `2 m`, calculate the gross lift of the wing.
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is `10cm^2`, the water velocity is `1ms^-1` and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is `5cm^2`, is........Pa. (Density of water `=10^3kg.m^-3`)
View SolutionCalculate the rate of flow of glycerine of density. `1.25xx10^(3) kg//m^(3)` through the conical section of a pipe. If the radii of its ends are `1.0m` and `0.04m` and the pressure drop across its length is `10N//m^(2)`.
View SolutionA cylindrical vessel contains a liquid of density `rho` up to height `h`. The liquid is closed by a piston of mass `m` and area of cross section `A`. There is a small hole at the bottom of the vessel. The speed `v` with which the liquid comes out of the hole is

View SolutionA pump draws water from a reservoir and sends it through a horizontal pipe with speed v. Find the relation between power of the pump and velocity of liquid.
View SolutionThere are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density `rho`. The differences in height between the holes is `h`. The tank is resting on a smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it in equilibrium is
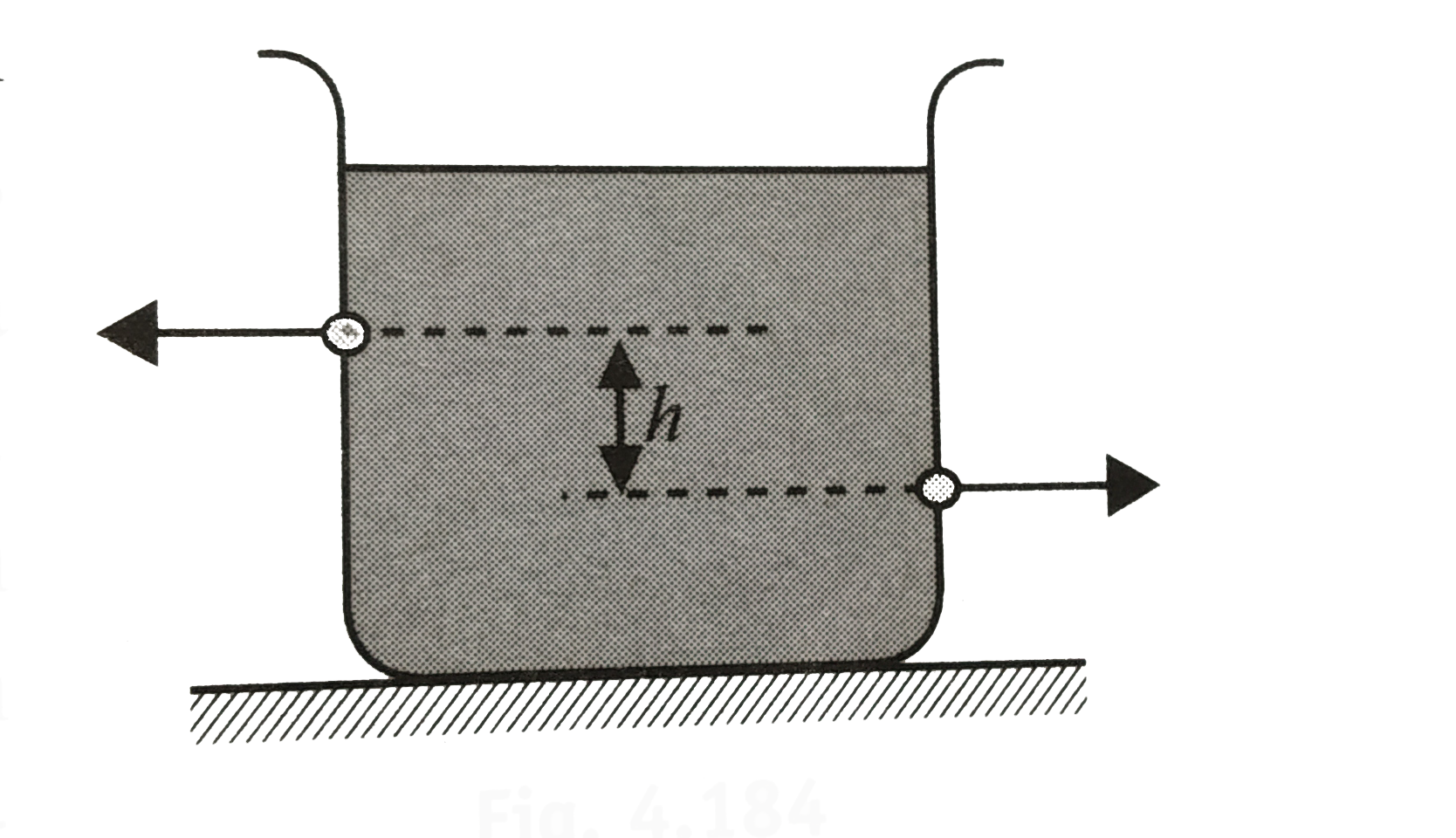
View SolutionEqual volume of two immiscible liquids of densities `rho` and `2rho` are filled in a vessel as shown in the figure. Two small holes are punched at depths `h//2` and `3h//2` from the surface of lighter liquid. If `v_(1)` and `v_(2)` are the velocities of efflux at these two holes, then `v_(1)//v_(2)` is
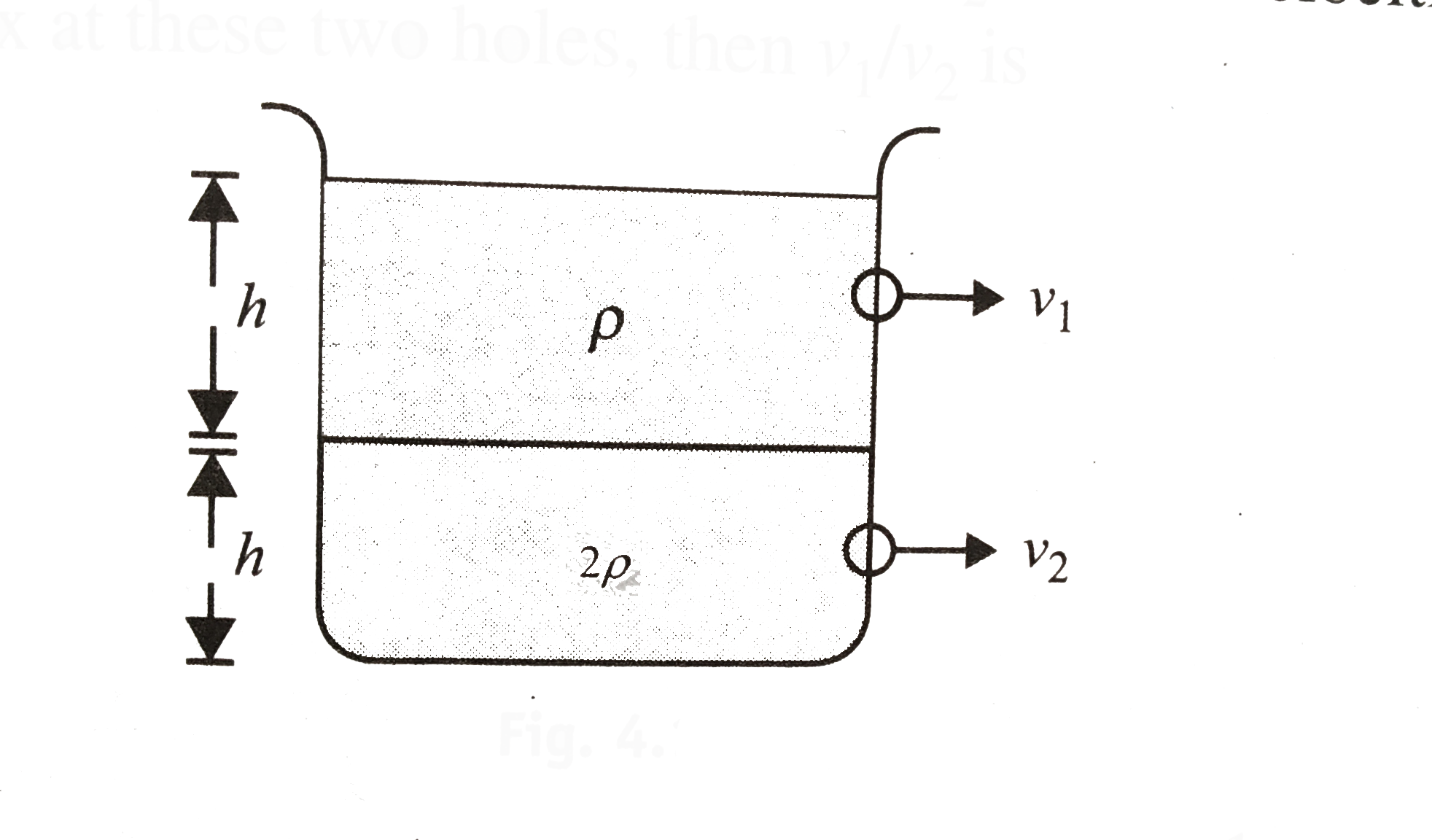
View SolutionA hose shoots water straight up to a height of 2.5 m. The opening end of the hose has an area of `0.75cm^(2)`. What is the speed of the water as it leaves the hose? How much water will come out in one minute?
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA large wooden plate of area `10m^2` floating on the surface of river is made to move horizontally wilth a speed of `2ms^-1` by applying a tangential force. If the river is 1m deep and the water contact with the bed is stationary, find the tangential force needed to keep the plate moving. Coefficient of viscosity of water at the temperature of the river `=10^-2 poise.`
View SolutionA `16cm^(3)` of water flows per second through a capillary tube of radius `r` cm and of length 1 cm, when connected to a pressure head of `h` cm of water. If a tube of the same length and radius `r//2` is connected to the same pressure head, find the mass of watear flowing per minute through the tube.
View SolutionWater flows in a streamline manner through a cappilary tube of radius a. The pressure difference being P and the rate of flow is Q . If the radius is reduced to `a//2` and the pressure difference is increased to 2P, then find the rate of flow.
View SolutionCapillary tubes of length `l` and `2l` are connected in series, their radii are r and `2r` respectively. If stream line flow is maintained and pressure difference across first and second capillary tubes are `P_(1)` and `P_(2)` respectively then find the ratio `(P_(1))/(P_(2))`.
View SolutionThree capillary tubes of same radius 1 cm but of length 1 m 2 m and 3 m are fitted horizontally to the bottom of a long vessel containing a liquid at constant pressure and flowing through these. Whatis the length of a single tube which can replace the three capillaries.
View SolutionTwo equal drops of water are falling through air with a steady velocity v. If the drops coalesced, what will be the new velocity?
View SolutionA spherical steel ball released at the top of along column of glycerin of length `l` falls through a distance `l//2` with accelerated motion and the remaining distance `l//2` with uniform velocity let `t_(1)` and `t_(2)` denote the times taken to cover the first and second half and `w_(1)` and `w_(2)` are the work done against gravity in the two halves, then compare times and work done.
View SolutionA small steel ball falls through a syrup at a constant speed of `10cms^-1`. If the steel ball is pulled upwards with a force equal to twice its effective weight, how fast will it move upwards?
View SolutionA small piece of wire of length 4 cm is floating on the surface of water. If a force of 560 dynes in excess of itss apparent weight is requried to pull it up from the surface find the surface tension of water.
View SolutionAn annular metal ring of inner radius 7 cm and outer radius 14 cm and negligible weight is floating on the surface of a liquid if surface tensiton of liquid is `0.08Nm^(-1)` calculate the force required to detach it it from liquid surface.
View SolutionA wire is bent in the form of a `U`-shape and a slider of negligible mass is connecting the two vertical sides of the U-shape. This arrangement is dipped in a soap solution and lifted a thin soap film is formed in t he frame it supports a wegith of `2.0xx10^(-2)` if the length of the slider is 40 cm whta is the surface tension of the film?
View SolutionWhen a wire o length `l(lltltr)` and ceoss sectional radius `r` is kept floating on surface of a liquid. Maximum radius of wire such that it may not sink. Is
View SolutionIf the surface tension of soap solution is `35"dynes"//cm`, calculate the work done to form an air bubble of diameter 14 mm with that solution.
View SolutionA soap bubble is blown to a radius of 3 cm. if it is to be further blown to a radius of 4 cm what is the work done? (surface tension of soap solution `=3.06xx10^(-2)Nm^(-1))`
View SolutionA water drop of diameter 2 mm is split up into `10^(9)` identical water drops. Calculate the work done in this process. (the surface tension of water is `7.3xx10^(-2)Nm^(-1))`
View Solution1000 drps of a liquid each of diameter 4 mm coalesce to form a single large drop. If surface tension of liquid is 35 dyne `cm^(-1)` calculate the energy evolved by the system in the process.
View SolutionA large number of liquid drops each of radius 'a' coalesce to form a single spherical drop of radish b. The energy released in the process is converted into kinetic energy of the big drops formed. The speed of big drop will be
View SolutionA drop of radius R is split under isothermal condition into into `n` droplets each of radius `r` the ratio of surface energies of big and each small drop is
View SolutionNumber of droplets (n) are combined isothermally to form a big drop the ratio of initial and final surface energies of the system is
View SolutionWhen a big drop of water is formed from n small drops of water, the energy oss is 3E, where, E is the energy of the bigger drop. If R is the radius of the bigger drop and r is the radius of the smaller drop then number of smaller drops (n) is?
View SolutionFind the weight of water supported by surface tension in a capillary tube with a radius of 0.2 mm. Surface tension of water is `0.072Mn^(-1)` and angle of contact of water is `0^(0)`.
View SolutionA capillary tube of radius `r` is immersed in water and water rises to a height of `h` mass of water in the capillary tube is `5xx10^(-3)` kg the same capillary tube is now immersed in a liquid whose surface tension in `sqrt(2)` times the surface tension of water. The angle of contact between the capillary tu8be and this liquid is `45^(@)` the mass of liquid which rises into the capillary tube now is (in kg)
View SolutionA U tube is supported with its limbs vertical and is partly filled with water. If the inner diameter of the limbs are 1cm,and 0.01 cm , respectively, what will be the difference in height of water in the two limbs? S.T. or water `70 xx 10^(-3) Nm^(-1)`. Angle of contact , `theta = 0^(@)`.
View SolutionWhat should be the pressure inside a small air bubble of `0.1 mm` radius situated just below the surface of water? Surface tension of water `=72xx10^(-3)N//m` and atmospheric pressure `=1.013xx10^(5)N//m^(2)`
View SolutionTwo separate air bubbles (radii `0.002 cm` and `0.004`) formed of the same liquid (surface tension `0.07 N//m`) come together to form a double bubble. Find the radius and the sense of curvature of the internal film surface common to both the bubbles.
View SolutionTwo soap bubble of radii `R_(1)` and `R_(2)` are kept in vacuum at constant temperature, the ratio of masses of air inside them, is
View SolutionTwo soap bubble of radii `R_(1)` and `R_(2)` are in atmosphere of pressure `P_(0)` at constant temperature. Ratio of masses of air inside them is
View SolutionTwo spherical soap bubble coalesce. If `V` is the consequent change in volume of the contained air and `S` the change in total surface area, show that
`3PV+4ST=0`
where `T` is the surface tension of soap bubble and `P` is
Atmospheric pressure
View SolutionWhen air bubble comes from bottom to the top of a lake its radius becomes n times. If temprerature remains constant through out the lake the depth of the lake will be.
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is `7.30 xx 10^(-2) Nm^(-1)`. 1 atmospheric pressure =` 1.01 xx 10^(5) Pa`, density of water `= 1000 kg//m^(3), g=9.80 ms^(-2)`. also calculate the excess pressure.
View SolutionA glass U-tube is such that the diameter of one limb is `3.0mm` and that of the other is 6.0mm. The tube is inverted vertically with the open ends below the surface of water in a beaker. What is the difference between the height to which water rises in the two limbs? Surface tension of water is `0.07Nm^(-1)`. Assume that the angle of contact between water and glass is `0^(@)`.
View Solution
Examples questions and complete solutions for chapter MECHANICAL PROPERTIES OF FLUIDS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- C.U.Q
- C.U.Q (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM)
- C.U.Q (TORRICELLI.S THEOREM AND VISCOSITY)
- C.U.Q(POISEUILLE.S EQUATION)
- C.U.Q(PRESSURE, FORCE OF BUOYANCY, LAWS OF FLOATATION)
- Comprehension Type Questions
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 10
- EVALUATE YOURSELF - 11
- EVALUATE YOURSELF - 12
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EVALUATE YOURSELF - 5
- EVALUATE YOURSELF - 6
- EVALUATE YOURSELF - 7
- EVALUATE YOURSELF - 8
- EVALUATE YOURSELF - 9
- Examples
- EXERCISE - I - (C.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - I - (C.W) (COEFFICIENTY OF VISCOSITY & VISCOUS FORCE)
- EXERCISE - I - (C.W) (COMBINATION OF DROPS & BUBBLES)
- EXERCISE - I - (C.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND APPLICATIONS)
- EXERCISE - I - (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND SOAP BUBBLE)
- EXERCISE - I - (C.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - I - (C.W) (POISEUILLE.S EQUATION)
- EXERCISE - I - (C.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - I - (C.W) (TERMINAL VELOCITY & VISCOUS FORCE)
- EXERCISE - I - (C.W) (TORRICELLI.S THEOREM)
- EXERCISE - I - (H.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - I - (H.W) (COEFFICIENT OF VISCOSITY & VISCOUS FORCE)
- EXERCISE - I - (H.W) (COMBINATION OF DROPS & BUBBLES)
- EXERCISE - I - (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - I - (H.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND SOAP BUBBLE)
- EXERCISE - I - (H.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - I - (H.W) (POISEUILLE.S EQUATION)
- EXERCISE - I - (H.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - I - (H.W) (REYNOLDS NUMBER)
- EXERCISE - I - (H.W) (TERMINAL VELOCITY)
- EXERCISE - I - (H.W) (TORRICELLI.S THEOREM)
- EXERCISE - I - (H.W) (VARIATION OF PRESSURE, UPTHRUST)
- EXERCISE - I - (H.W) (WORK & SURFACE ENERGY)
- EXERCISE - II (C.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - II (C.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - II (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND IN A SOAP BUBBLE)
- EXERCISE - II (C.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - II (C.W) (POISEUILLE.S EQUATION)
- EXERCISE - II (C.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - II (C.W) (TERMINAL VELOCITY)
- EXERCISE - II (C.W) (TORRICELLI.S THEOREM)
- EXERCISE - II (C.W) (VARIATION OF PRESSURE, UPTHRUST)
- EXERCISE - II (C.W) (WORK & SURFACE ENERGY)
- EXERCISE - II (H.W) (CAPILLARITY AND CAPILLARY RISE)
- EXERCISE - II (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - II (H.W) (EXCESS PRESSURE IN A LIQUID DROP AND IN A SOAP BUBBLE
- EXERCISE - II (H.W) (POISEUILLE.S EQUATION)
- EXERCISE - II (H.W) (PORCE DUE TO SURFACE TENSION)
- EXERCISE - II (H.W) (TORRICELLI.S THEOREM)
- EXERCISE - II (H.W) (VARIATION OF PRESSURE AND UPTHRUST)
- EXERCISE - II (H.W) (WORK & SURFACE ENERGY)
- EXERCISE - III
- Illustration
- Level 1 (C.W)
- Level 1 (H.W)
- Level 2 (C.W)
- Level 2 (H.W)
- Level 3
- More Than One Alternative Type Question
- Paragraph Type Questions
- Single Answer Questions
- Statement Type Questions