Complete Solutions to Comprehension Type Questions of chapter MECHANICAL PROPERTIES OF FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| NARAYANA | Comprehension Type Questions |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
In figure, block `A` hangs by a cord form spring balance `D` and it submerged in a liquid `C` contained in a beaker `B`. The mass of the beaker is `1 kg`. The mass of the liquid is `1.5 kg`. Balance `D` reads `7.5 kg`. The volume of block `A` is `0.003 m^(3)`. The mass per unit volume of the liquid is
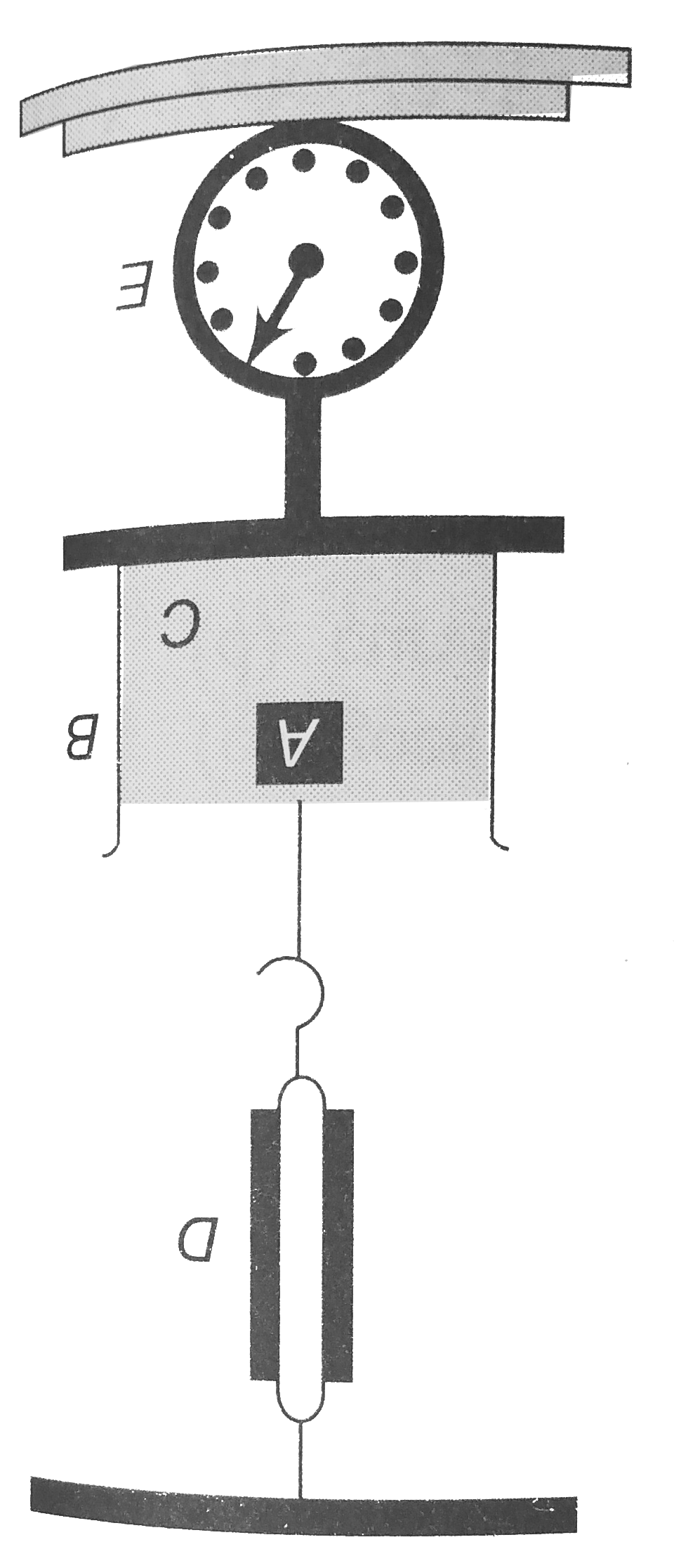
View SolutionAs Fig. shows, `S_(1)` and `S_(2)`, are spring balances. Block `A` is hanging from spring balance `S_(1)` and immersed in liquid `L` which is contained in beaker `B`. The mass of beaker `B` is `1 kg` and mass of liquid `L` is `1.5 kg`. Balances `S_(1)` and `S_(2)` reads `2.5 kg` and `7.5 kg`, respectively. What will be the readings of `S_(1)` and `S_(2)` when block `A` is pulled up out of the liquid. Find the reading of `S_(1)` and `S_(2)`?

View SolutionAs Fig. shows, `S_(1)` and `S_(2)`, are spring balances. Block `A` is hanging from spring balance `S_(1)` and immersed in liquid `L` which is contained in beaker `B`. The mass of beaker `B` is `1 kg` and mass of liquid `L` is `1.5 kg`. Balances `S_(1)` and `S_(2)` reads `2.5 kg` and `7.5 kg`, respectively. What will be the readings of `S_(1)` and `S_(2)` when block `A` is pulled up out of the liquid. Find the reading of `S_(1)` and `S_(2)`?

View Solution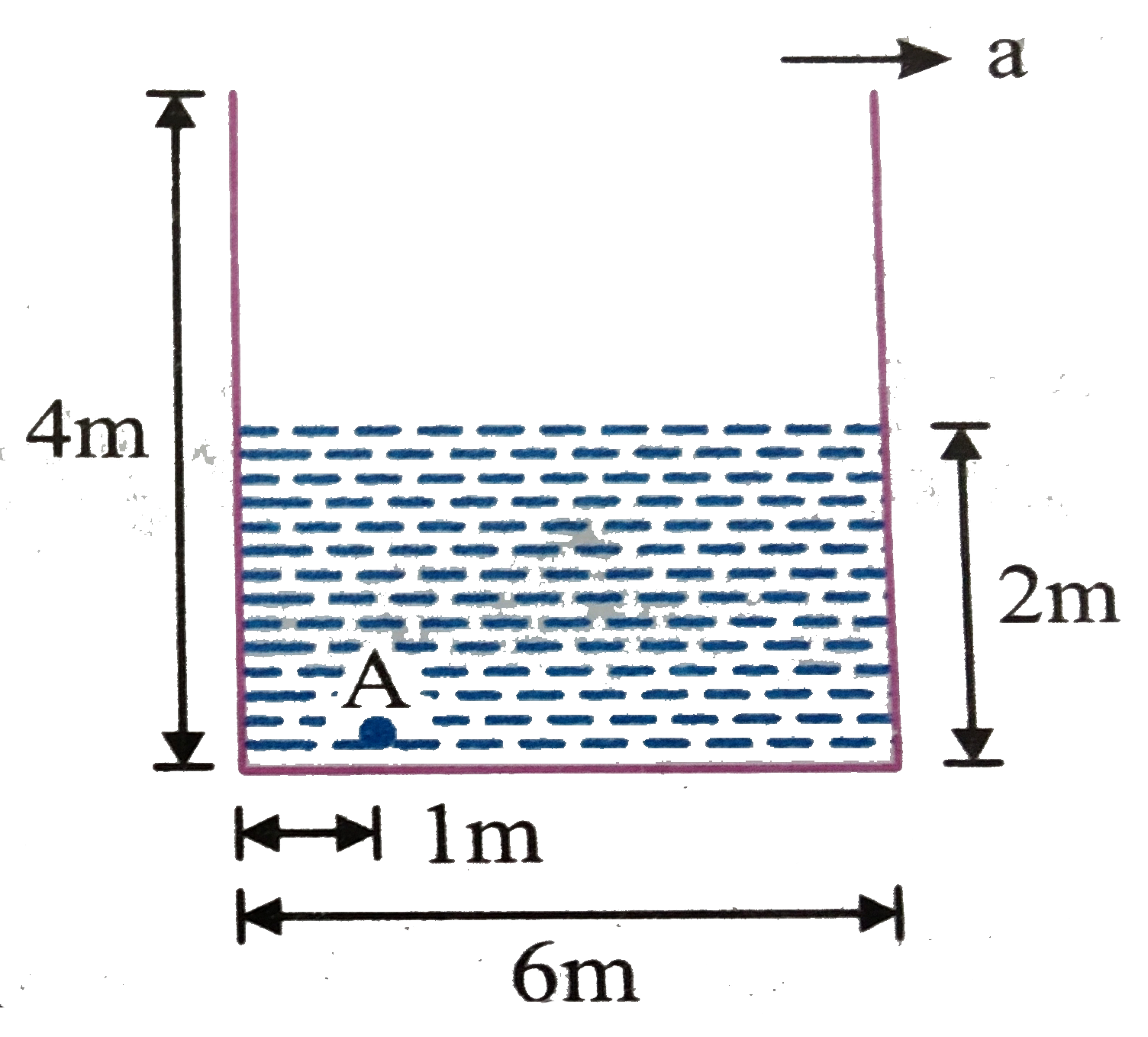
An open rectangular tank of dimensions `6mxx5mxx4m` contains water upto height of 2m. The vessel is accelerated horizontally with an acceleration of `am//s^(2)` as shown. Take `rho_("water")=10^(3)kg//m^(3)`
`g=10m//s^(2)` atmospheric pressure `=10^(5)N//m^(2)`. Bese on above information answer the following questions:
Determine the maximum value of a so that no water comes out from tan k.
View Solution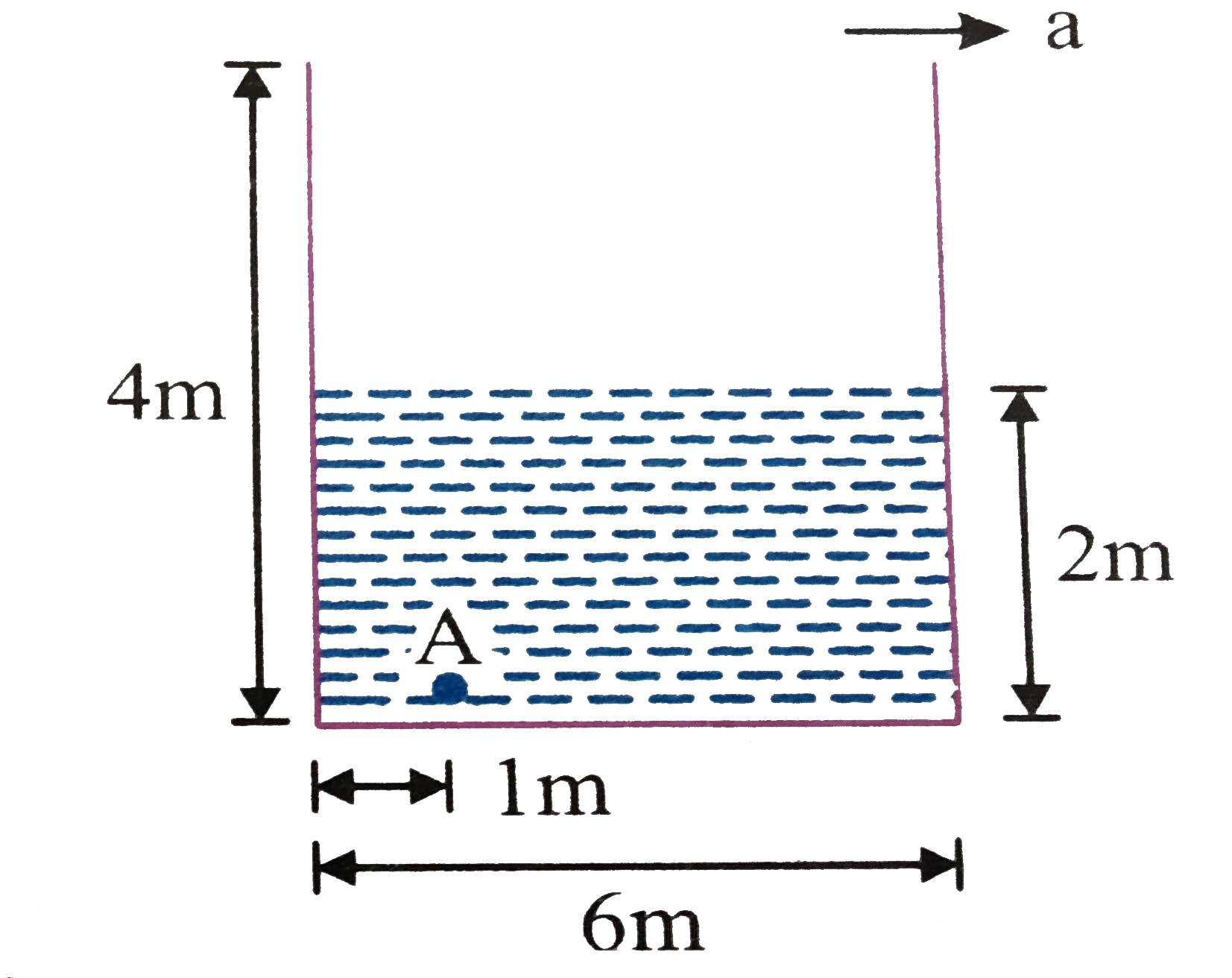
An open rectangular tank of dimensions `6mxx5mxx4m` contains water upto height of 2m. The vessel is accelerated horizontally with an acceleration of `a m//s^(2)` as shown. Take `rho_("water")=10^(3)kg//m^(3)`
`g=10m//s^(2)` atmospheric pressure `=10^(5)N//m^(2)`. Bese on above information answer the following questions:
Determine the height to which the water should be filled in the tank so that when `a=5m//s^(2)` no water comes out from the tank
View Solution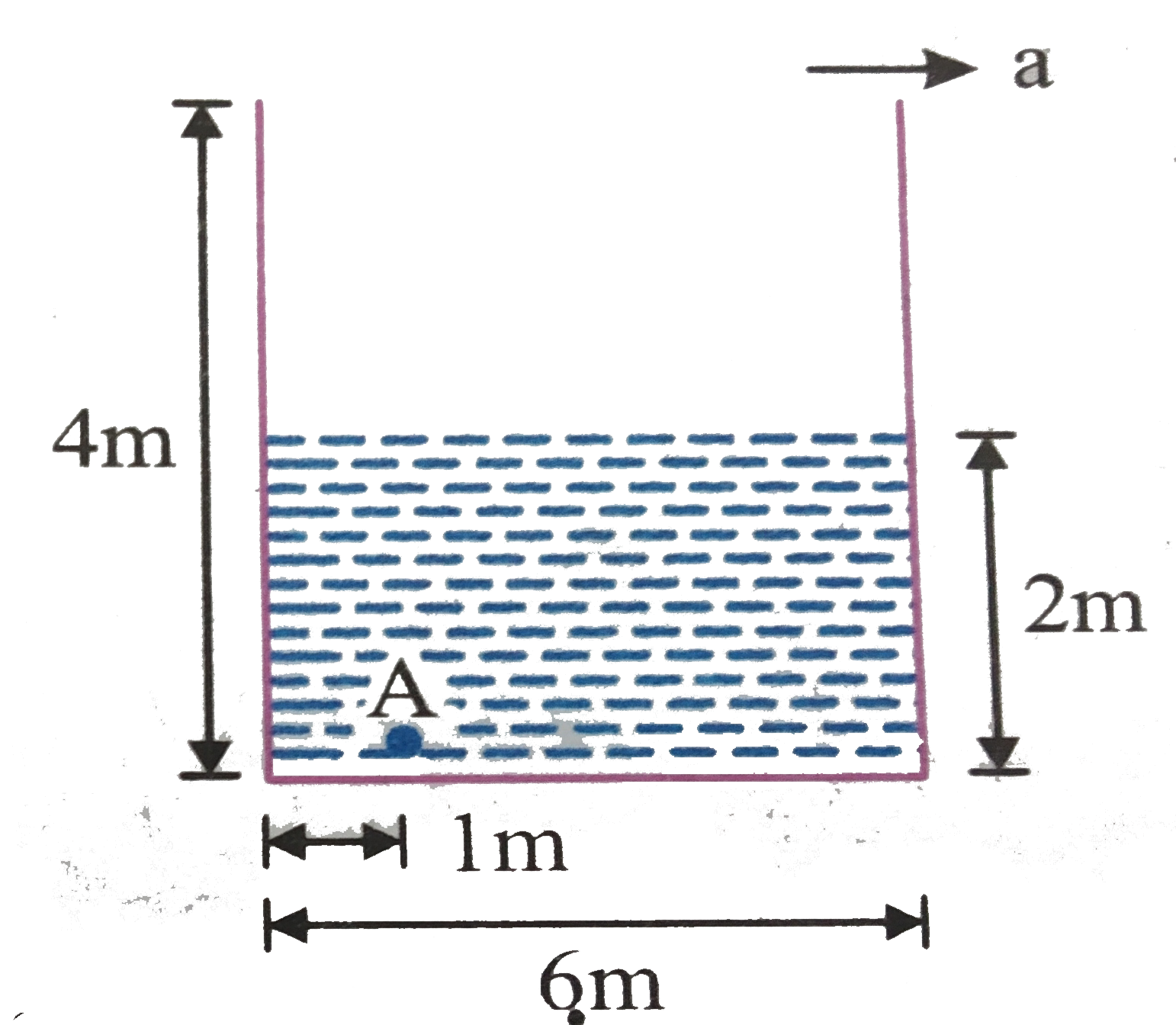
An open rectangular tank of dimensions `6mxx5mxx4m` contains water upto height of 2m. The vessel is accelerated horizontally with an acceleration of `a m//s^(2)` as shown. Take `rho_("water")=10^(3)kg//m^(3)`
`g=10m//s^(2)` atmospheric pressure `=10^(5)N//m^(2)`. Bese on above information answer the following questions:
Instead of open top if the vessel is closed then absolute pressure at point A would be [take `a=(20)/(3)m//s^(2)` and initially height of water in tank is 2m]
View SolutionA solid hemisphere of radius `R` is made to just sink in a liquid of density `rho`. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
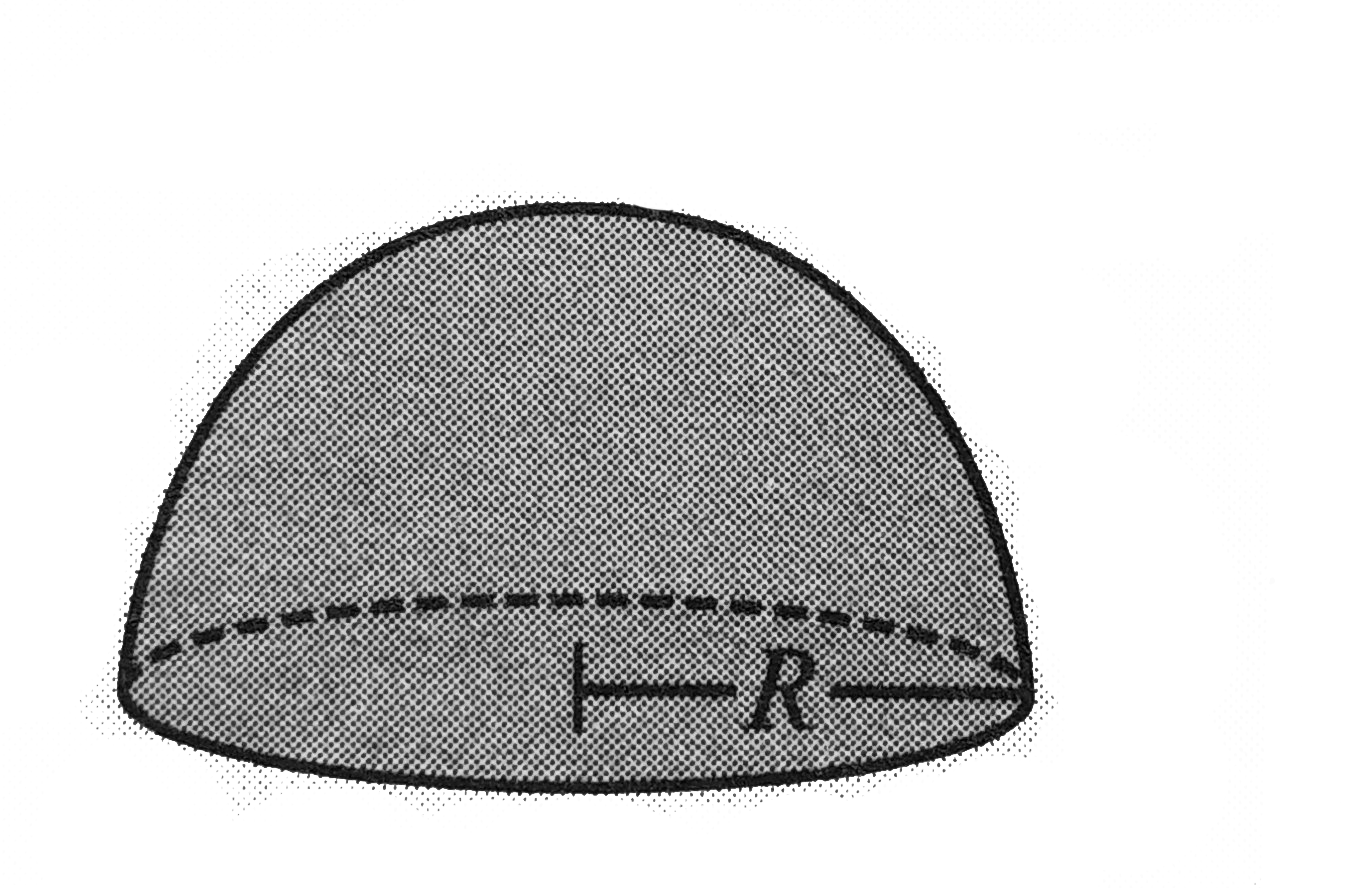
View SolutionA solid hemisphere of radius `R` is made to just sink in a liquid of density `rho`. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.

View Solution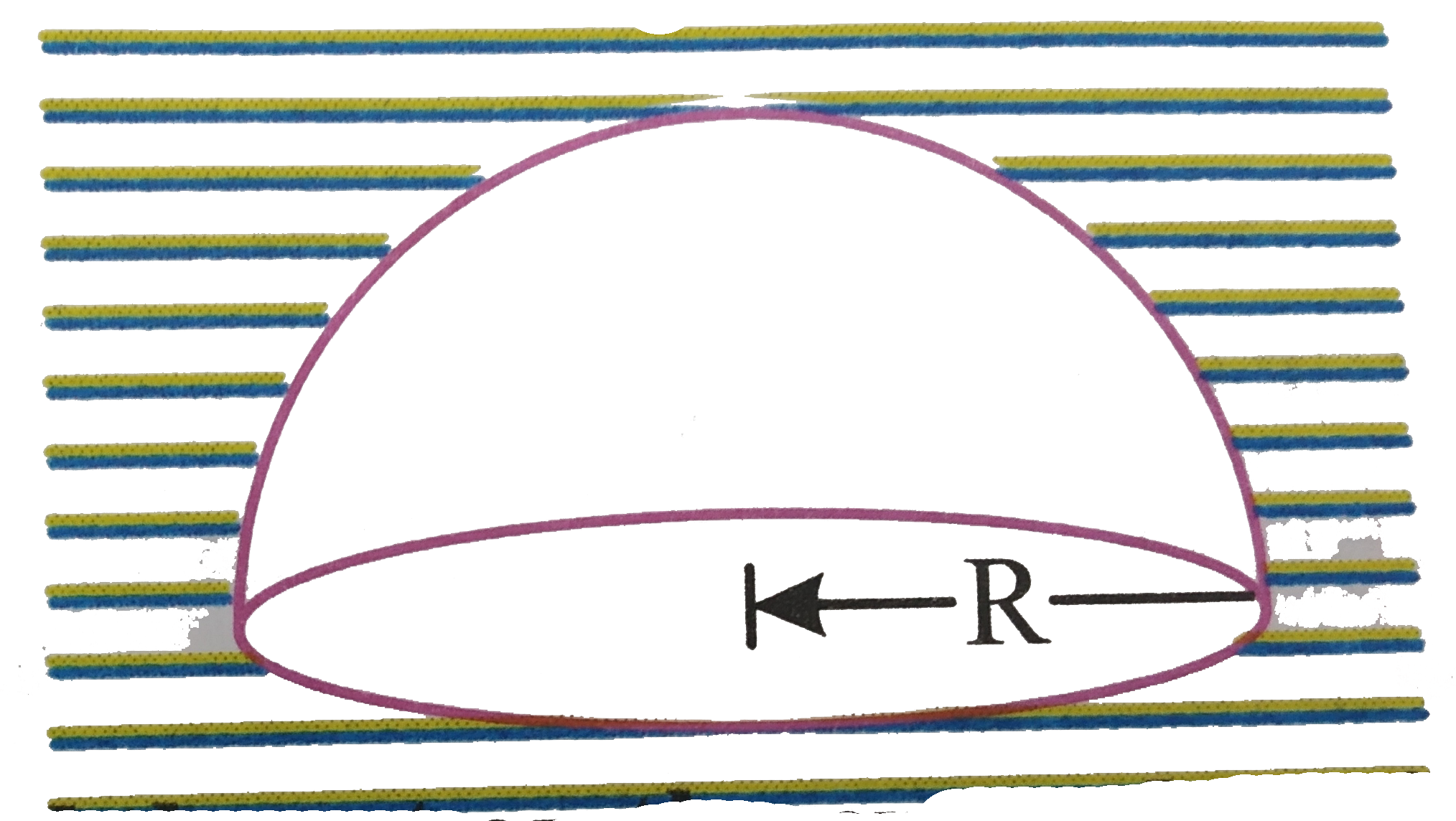
A solid hemisphere of radius `R` is made to just sink in a liquid of density `rho` find the
View Solution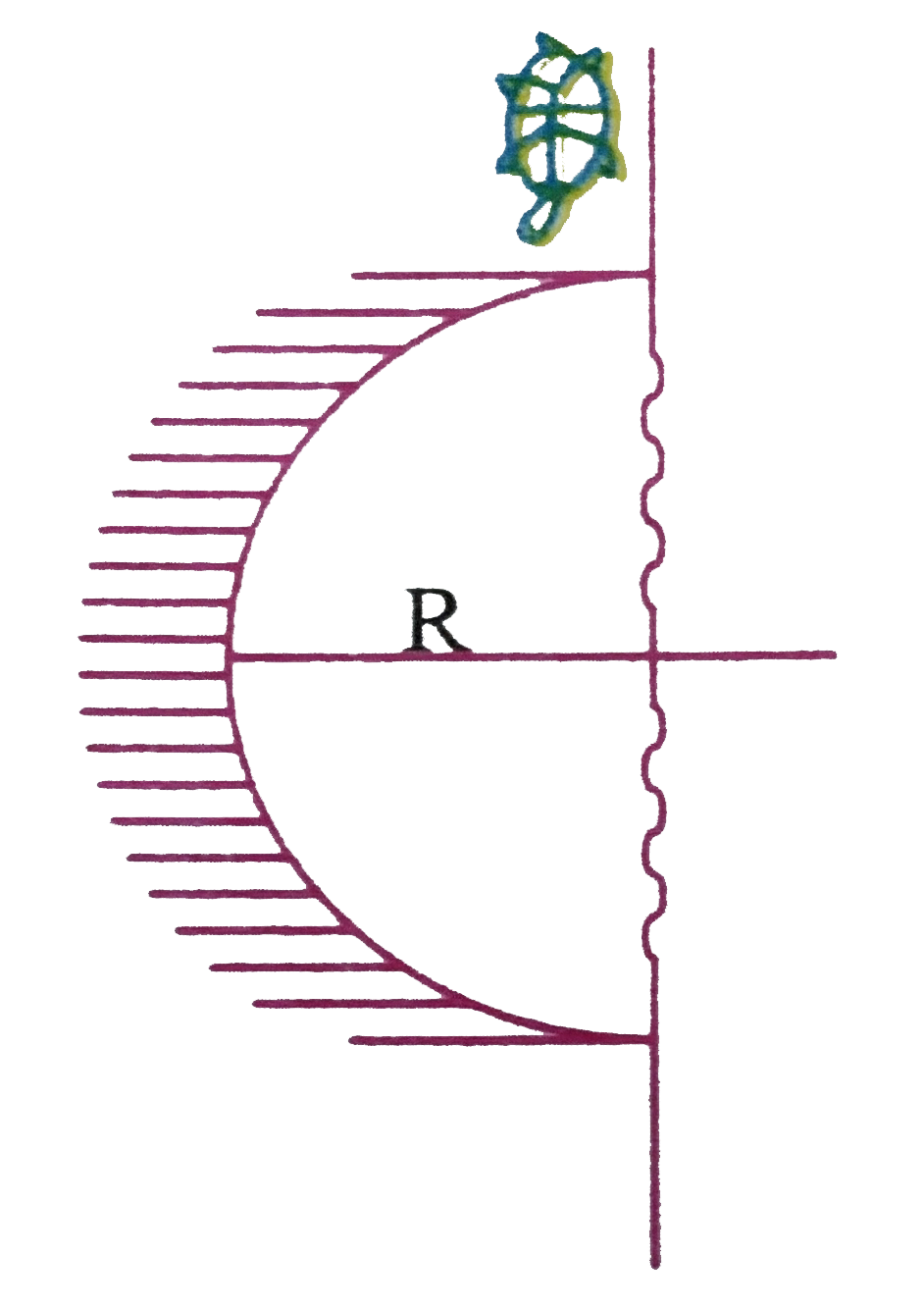
A tortoise is just sinking in water of density `rho` The tortoise is assumed to be3 a hemisphere of radius `R`.
Find vertical thrust
View Solution
A tortoise is just sinking in water of density `rho` The tortoise is assumed to be3 a hemisphere of radius `R`.
Q. Find the total hydrostatic force
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height `h_(0)` and pressure `2p_(0)` where `rh_(0)` is the atmospheric pressure. There is a hole in the wall of the tank at a depth `h_(1)` below the top from which water comes out. A long vertical tube is connected as shown.

Find the height `h_(2)` of the water in the long tube above top initially.
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height `h_(0)` and pressure `2p_(0)` where `rh_(0)` is the atmospheric pressure. There is a hole in the wall of the tank at a depth `h_(1)` below the top from which water comes out. A long vertical tube is connected as shown.

Find the speed with which water comes out of the hole
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height `h_(0)` and pressure `2p_(0)` where `rh_(0)` is the atmospheric pressure. There is a hole in the wall of the tank at a depth `h_(1)` below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
View SolutionA uniform solid cylinder of density `0.8g//cm^3` floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are `0.7g//cm^3` and `1.2g//cm^3`, respectively. The height of liquid A is `h_A=1.2cm.` The length of the part of the cylinder immersed in liquid B is `h_B=0.8cm`.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionA uniform solid cylinder of density `0.8g//cm^3` floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are `0.7g//cm^3` and `1.2g//cm^3`, respectively. The height of liquid A is `h_A=1.2cm.` The length of the part of the cylinder immersed in liquid B is `h_B=0.8cm`.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionA uniform solid cylinder of density `0.8g//cm^3` floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are `0.7g//cm^3` and `1.2g//cm^3`, respectively. The height of liquid A is `h_A=1.2cm.` The length of the part of the cylinder immersed in liquid B is `h_B=0.8cm`.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.

If the piston is pushed at a speed of `5mms^-1`, the air comes out of the nozzle with a speed of
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.
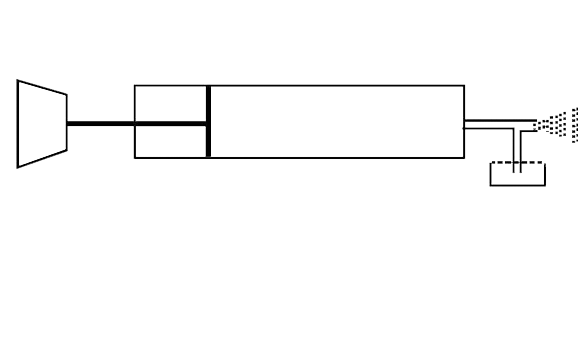
If the density of air is `rho_a`, and that of the liquid `rho_l`, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to
View SolutionA wooden cylinder of length L is partly submerged in a liquid of specific gravity `rho_(1)` with `n^(th) (nlt1)` part of it inside the liquid. Another immiscible liquid of density `rho_(2)` is poured to completely submerge the cylinder. Density of cylinder `rho` is the geometric mean of the densities of the two liquid.
Express the density of upper liquid in terms of density of cylinder
View SolutionA wooden cylinder of length L is partly submerged in a liquid of specific gravity `rho_(1)` with `n^(th)` `(nlt1)` part of it inside the liquid. Another immiscible liquid of density `rho_(2)` is poured to completely submerge the cylinder. Density of cylinder `rho` is the geometric mean of the densities of the two liquid.
Calculate the fraction of the cylinder submerged in the lower liquid after the upper liquid is poured in the vessel
View SolutionA wooden cylinder of length L is partly submerged in a liquid of specific gravity `rho_(1)` with `n^(th)` `(nlt1)` part of it inside the liquid. Another immiscible liquid of density `rho_(2)` is poured to completely submerge the cylinder. Density of cylinder `rho` is the geometric mean of the densities of the two liquid.
When the cylinder is slightly depressed and released, it oscillates. let there be a mean position. find the time period of small oscillations below thee mean position
View SolutionA wooden cylinder of length L is partly submerged in a liquid of specific gravity `rho_(1)` with `n^(th)` `(nlt1)` part of it inside the liquid. Another immiscible liquid of density `rho_(2)` is poured to completely submerge the cylinder. Density of cylinder `rho` is the geometric mean of the densities of the two liquid.
Similarly as above, find the time period of small oscillations above the mean position.
View SolutionA tank of height `H` and base area `A` is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area `(A)/(3)` and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
The speed of water flowing out of the orifice after the cylinder is kept inside it is
View SolutionA tank of height `H` and base area `A` is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area `(A)/(3)` and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to `(H)/(2)`, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View Solution
A spherical ball of radius R is floating at the interface of two liquids with densities `rho` and `2rho`. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
Find the force exerted by the liquid with density `2rho` on the ball
View Solution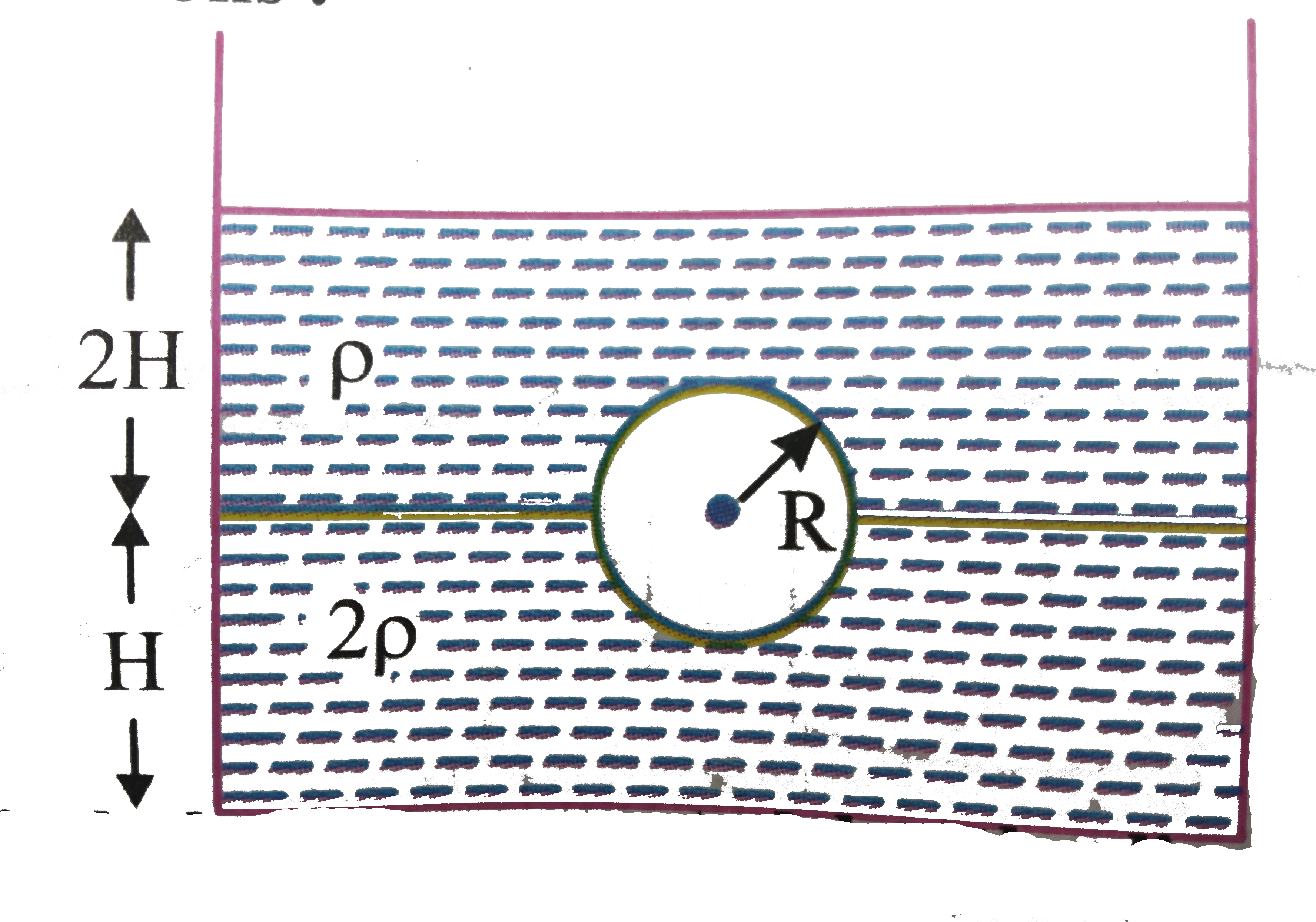
A spherical ball of radius R is floating at the interface of two liquids with densities `rho` and `2rho`. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
If a hole is drilled at the bottom of the vessel then volume of the ball immersed inliquid with density `rho` will
View Solution
An ideal liquid of density `rho` is filled in a horizontally fixed syringe fitted with a piston. There is no friction between the piston and the inner surface of the syringe. Cross-sectional area of the syringe is A. At one end of the syringe, an orifice is made. When the piston is pushed into the syringe, the liquid comes out of the orifice and then following a parabolic path falls on the ground.
With what velocity does the liquid come out of the orifice?
View Solution
An ideal liquid of density `rho` is filled in a horizontally fixed syringe fitted with a piston. There is no friction between the piston and the inner surface of the syringe. Cross-sectional area of the syringe is A. At one end of the syringe, an orifice is made. When the piston is pushed into the syringe, the liquid comes out of the orifice and then following a parabolic path falls on the ground.
With what velocity the liquid strikes the ground?
View SolutionMolecular forces exist between the molecules of a liquid in a container. The molecules on the surface have unequal force leading to a tension on the surface. If this is not compensated by a force, the equilibrium of the liquid will be a difficult task. This leads to an excess pressure on the surface. The nature of the meniscus can inform us of the direction of the excess pressure. The angle of contact of the liquid decided by the forces between the molecules, air and container can make the angle of contact.
The direction of the excess pressure in the meniscus of a liquid of angle of contact `2pi//3` is
View SolutionMolecular forces exist between the molecules of a liquid in a container. The molecules on the surface have unequal force leading to a tension on the surface. If this is not compensated by a force, the equilibrium of the liquid will be a difficult task. This leads to an excess pressure on the surface. The nature of the meniscus can inform us of the direction of the excess pressure. The angle of contact of the liquid decided by the forces between the molecules, air and container can make the angle of contact.
If the excess pressure in a soap bubble is `p`, the excess pressure in an air bubble is
View SolutionMolecular forces exist between the molecules of a liquid in a container. The molecules on the surface have unequal force leading to a tension on the surface. If this is not compensated by a force, the equilibrium of the liquid will be a difficult task. This leads to an excess pressure on the surface. The nature of the meniscus can inform us of the direction of the excess pressure. The angle of contact of the liquid decided by the forces between the molecules, air and container can make the angle of contact.
In a meniscus of radius `r`, with excess pressure p in atmospheric pressure `p_(0)`, the force experienced is
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is `P_0`, the pressure at point A is
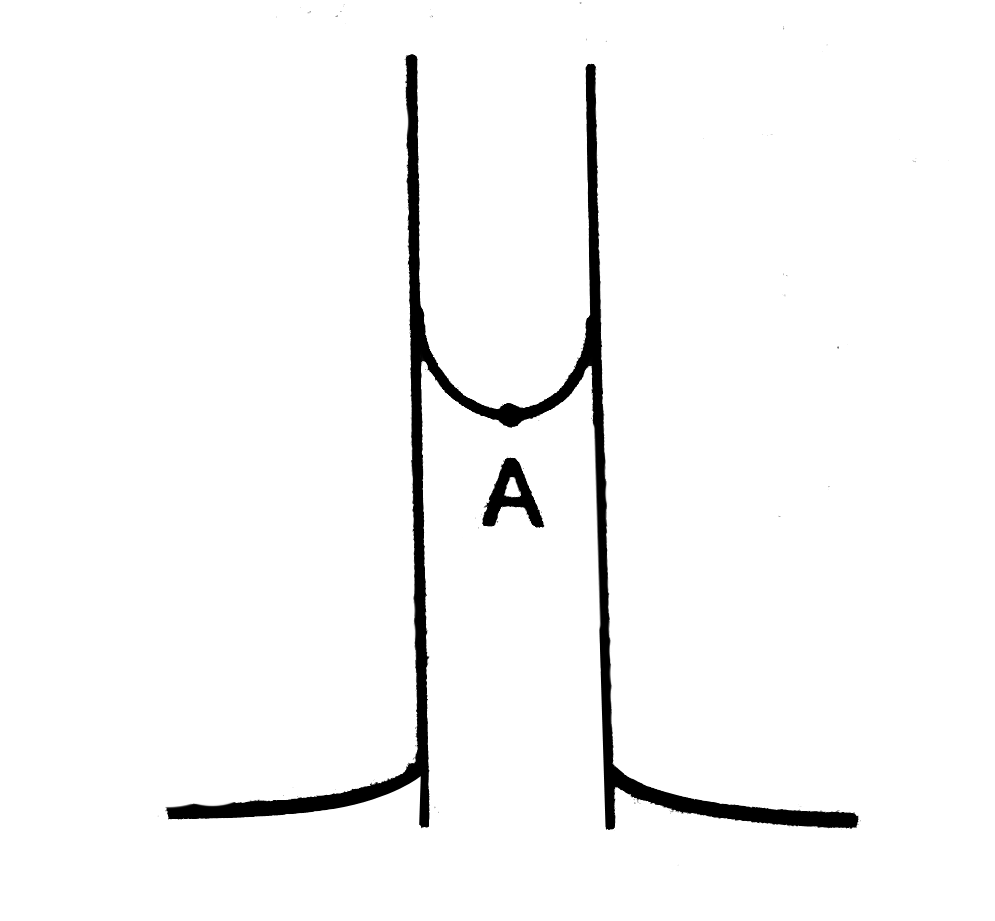
View SolutionFigure shows a capillary tube of radius r dipped into water. The atmospheric pressure is `P_(0)` and the capillary rise of water is `h`. `s` is the surface tension for water-glass.

Initially, `h = 10 cm`. If the capillary tube is now incline at `45^@`, the length of water rising in the tube will be
View SolutionWhich of the following graphs may represent the relation between capillary rise h and the radius r of the capillary
View SolutionSurface tension arises from the cohesive force between the surface molecules. Interplay between cohesion and adhesion force make the surface inclined at acute or obtuse angle with the contacting solid surfaces. This causes a capillary rise (or fail) given as `h=(2Tcostheta)/(rhogr)`, where `theta=` angle of contact `T=` surface tension `rho=` density of the liquid, `g=` acceleration due to gravity and `r=` radius of the capillary tube.
Q. In capillary action `theta` can be:
View SolutionSurface tension arises from the cohesive force between the surface molecules. Interplay between cohesion and adhesion force make the surface inclined at acute or obtuse angle with the contacting solid surfaces. This causes a capillary rise (or fail) given as `h=(2Tcostheta)/(rhogr)`, where `theta=` angle of contact `T=` surface tension `rho=` density of the liquid, `g=` acceleration due to gravity and `r=` radius of the capillary tube.
In capillary rise:
View SolutionSurface tension arises from the cohesive force between the surface molecules. Interplay between cohesion and adhesion force make the surface inclined at acute or obtuse angle with the contacting solid surfaces. This causes a capillary rise (or fail) given as `h=(2Tcostheta)/(rhogr)`, where `theta=` angle of contact `T=` surface tension `rho=` density of the liquid, `g=` acceleration due to gravity and `r=` radius of the capillary tube.
Q. If the vessel accelerates up, capillary rise,
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of te drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surfacetension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If the radius of the opening of the dropper is `r`, the vertical force due to the surface tension on the top of radius `R` (assuming `rltltR`) is
View SolutionWhen liquid medicine of density `rho` is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of te drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surfacetension T when the radius of the drop is R. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
If `r=5xx10^(-4)`m `overset(~)(n)=10^(3)kgm^(-3)`, `g=10ms^(-2)`, `T=0.11Nm^(-1)` the radius of the drop when it detaches from the dropper is approximately
View Solution
Comprehension Type Questions questions and complete solutions for chapter MECHANICAL PROPERTIES OF FLUIDS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- C.U.Q
- C.U.Q (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM)
- C.U.Q (TORRICELLI.S THEOREM AND VISCOSITY)
- C.U.Q(POISEUILLE.S EQUATION)
- C.U.Q(PRESSURE, FORCE OF BUOYANCY, LAWS OF FLOATATION)
- Comprehension Type Questions
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 10
- EVALUATE YOURSELF - 11
- EVALUATE YOURSELF - 12
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EVALUATE YOURSELF - 5
- EVALUATE YOURSELF - 6
- EVALUATE YOURSELF - 7
- EVALUATE YOURSELF - 8
- EVALUATE YOURSELF - 9
- Examples
- EXERCISE - I - (C.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - I - (C.W) (COEFFICIENTY OF VISCOSITY & VISCOUS FORCE)
- EXERCISE - I - (C.W) (COMBINATION OF DROPS & BUBBLES)
- EXERCISE - I - (C.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND APPLICATIONS)
- EXERCISE - I - (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND SOAP BUBBLE)
- EXERCISE - I - (C.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - I - (C.W) (POISEUILLE.S EQUATION)
- EXERCISE - I - (C.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - I - (C.W) (TERMINAL VELOCITY & VISCOUS FORCE)
- EXERCISE - I - (C.W) (TORRICELLI.S THEOREM)
- EXERCISE - I - (H.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - I - (H.W) (COEFFICIENT OF VISCOSITY & VISCOUS FORCE)
- EXERCISE - I - (H.W) (COMBINATION OF DROPS & BUBBLES)
- EXERCISE - I - (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - I - (H.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND SOAP BUBBLE)
- EXERCISE - I - (H.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - I - (H.W) (POISEUILLE.S EQUATION)
- EXERCISE - I - (H.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - I - (H.W) (REYNOLDS NUMBER)
- EXERCISE - I - (H.W) (TERMINAL VELOCITY)
- EXERCISE - I - (H.W) (TORRICELLI.S THEOREM)
- EXERCISE - I - (H.W) (VARIATION OF PRESSURE, UPTHRUST)
- EXERCISE - I - (H.W) (WORK & SURFACE ENERGY)
- EXERCISE - II (C.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - II (C.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - II (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND IN A SOAP BUBBLE)
- EXERCISE - II (C.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - II (C.W) (POISEUILLE.S EQUATION)
- EXERCISE - II (C.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - II (C.W) (TERMINAL VELOCITY)
- EXERCISE - II (C.W) (TORRICELLI.S THEOREM)
- EXERCISE - II (C.W) (VARIATION OF PRESSURE, UPTHRUST)
- EXERCISE - II (C.W) (WORK & SURFACE ENERGY)
- EXERCISE - II (H.W) (CAPILLARITY AND CAPILLARY RISE)
- EXERCISE - II (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - II (H.W) (EXCESS PRESSURE IN A LIQUID DROP AND IN A SOAP BUBBLE
- EXERCISE - II (H.W) (POISEUILLE.S EQUATION)
- EXERCISE - II (H.W) (PORCE DUE TO SURFACE TENSION)
- EXERCISE - II (H.W) (TORRICELLI.S THEOREM)
- EXERCISE - II (H.W) (VARIATION OF PRESSURE AND UPTHRUST)
- EXERCISE - II (H.W) (WORK & SURFACE ENERGY)
- EXERCISE - III
- Illustration
- Level 1 (C.W)
- Level 1 (H.W)
- Level 2 (C.W)
- Level 2 (H.W)
- Level 3
- More Than One Alternative Type Question
- Paragraph Type Questions
- Single Answer Questions
- Statement Type Questions