Complete Solutions to Single Answer Questions of chapter MECHANICAL PROPERTIES OF FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| NARAYANA | Single Answer Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. From the plot shown in figure, indicate the one that represents the velocity `(v)` of the pebble as a function of time `(t)`
01:40View SolutionWhich of the following diagrams does not represent a streamline flow?
01:14View SolutionAlong a streamline,
01:46View SolutionAn ideal fluid flows through a pipe of circular cross-section made of two sections with diameters `2.5 cm` and `3.75 cm`. The ratio of the velocities in the two pipes is
01:51View SolutionThe angle of contact at the interface of water glass is `0^(@)` ethylalcohol-glass is `0^(@)` mercury glas is `140^(@)` and methyliodide-glass is `30^(@)` A glass capillary is put in a through containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the through is
01:46View SolutionFor a surface molecule,
01:56View SolutionPressure is a scalar quantity, because
01:59View SolutionThe force required to take away flat plate of radius `4cm` from the surface of water is (surface tension os water `=70"dyne"//cm)`
01:27View SolutionThe surface tension of a soap solution is 0.05 `Nm^(-1)` How much work is done to produce a soap bubble of radius 0.03 m?
01:44View SolutionWater rises in a capillary tube to a height of 2.0cm. In another capillary tube whose radius is one third of it, how much the water will rise?
01:56View SolutionWater is flowing through a horizontal tube. The pressure of the liquid in the portion where velocity is `2m//s` is 2 m of Hg. What will be the pressure in the portion where velocity is `4m//s`
02:38View SolutionAir is streaming past a horizontal airplane wing such that its speed is `90 ms^(-1)` at the lower surface and `120 ms^(-1)` over the upper surface. The wing is `10 m` long and has an average width of `2 m`, the difference of pressure on the two sides and the gross lift on the wing respectively, are (density of air `=1.3kgm^(-3)`)
04:39View SolutionIn which of the following types of flows is the Bernoulli's theorem strictly applicable:
01:22View SolutionA U tube contains water and methylated spirts separated by mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5 cm of spirit in the other. What is the relative density of spirit?
02:30View SolutionIce berg floats in water with part of it submerged. What is the fraction of the volume of iceberg suberged, if the density of ice is `rho_(l)=0.917g//cm^(3)`?
02:03View Solution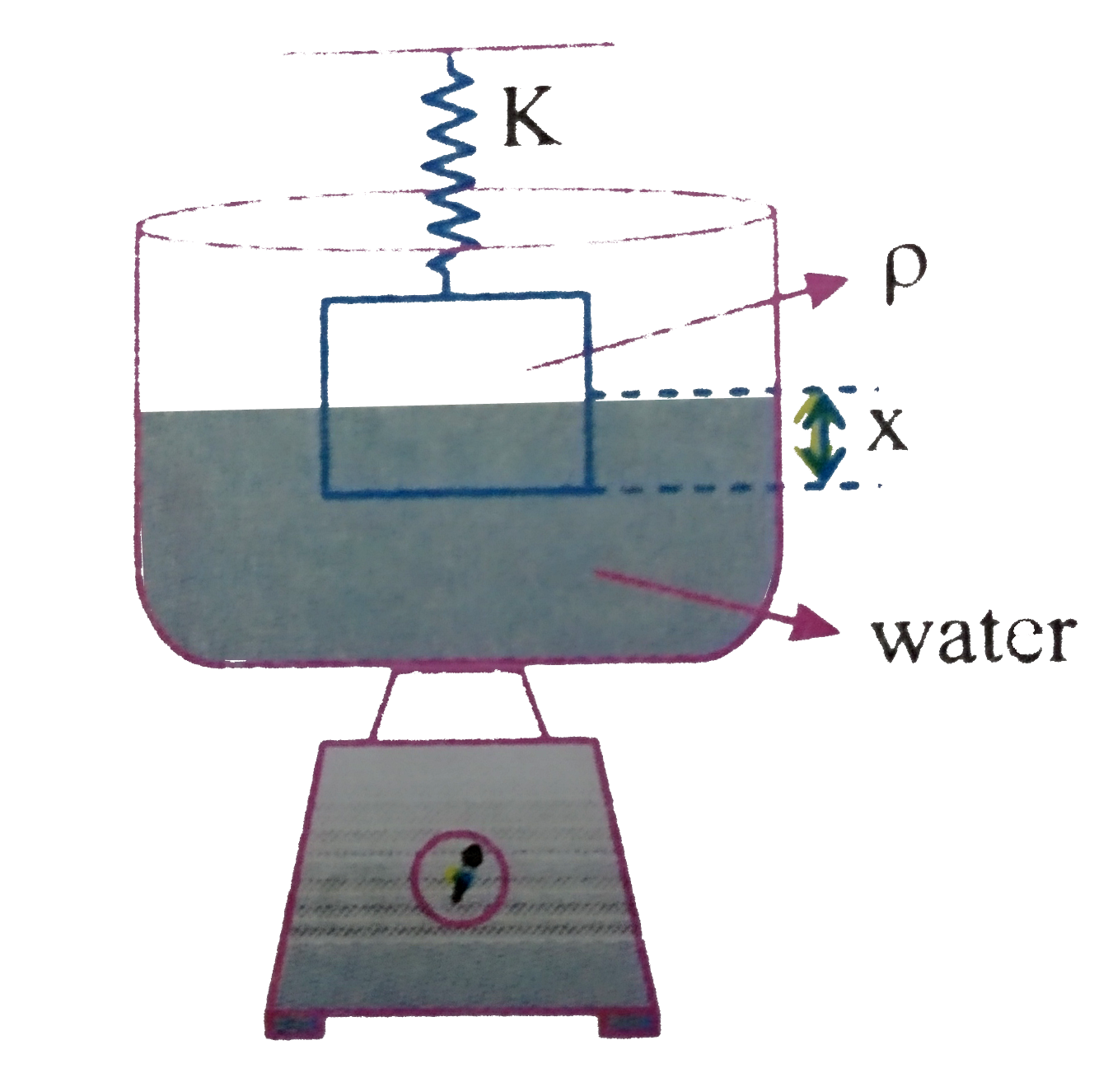
A vessel filled with water is kept on a weighing pan and the scale adjusted to zero. A block of mass 10 kg is suspended by a massless spring of spring constant `k=100N//m`. This block is submerged inside into the water in the vessel such that elongation i spring is `x=10cm`. What is the reading of the scale?02:02View SolutionTwo mercury droplets radii 0.1 cm and 0.2 cm collapse into one single drop. What amount of energy is released/absorbed? The sur4face tension of mercury `T=435.5xx10^(-3)Nm^(-1)`
06:38View SolutionThe surface tension and vapour pressure of water at `20^(@)C` is `7.28xx10^(-2)Nm^(-1)` and `2.33xx10^(3)Pa`, respectively. What is the radius of the smalalest spherical water droplet which can form without evaporating at `20^(@)C`?
01:55View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density `rho` where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
 04:07View Solution
04:07View Solution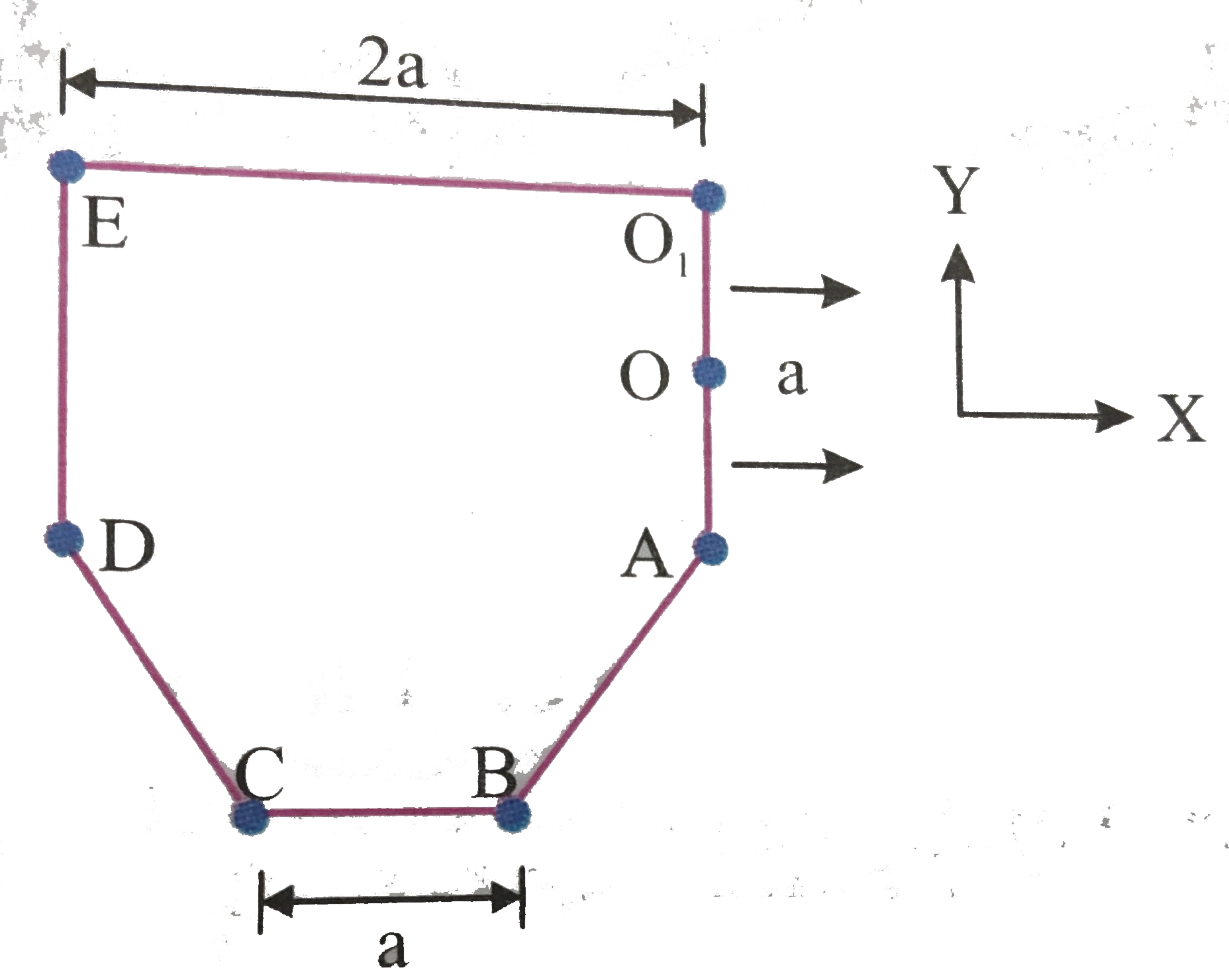
The top view of closed compartment containing liquid is moving with an acceleration along x-axis as shown. Find the incorrect statement01:51View Solution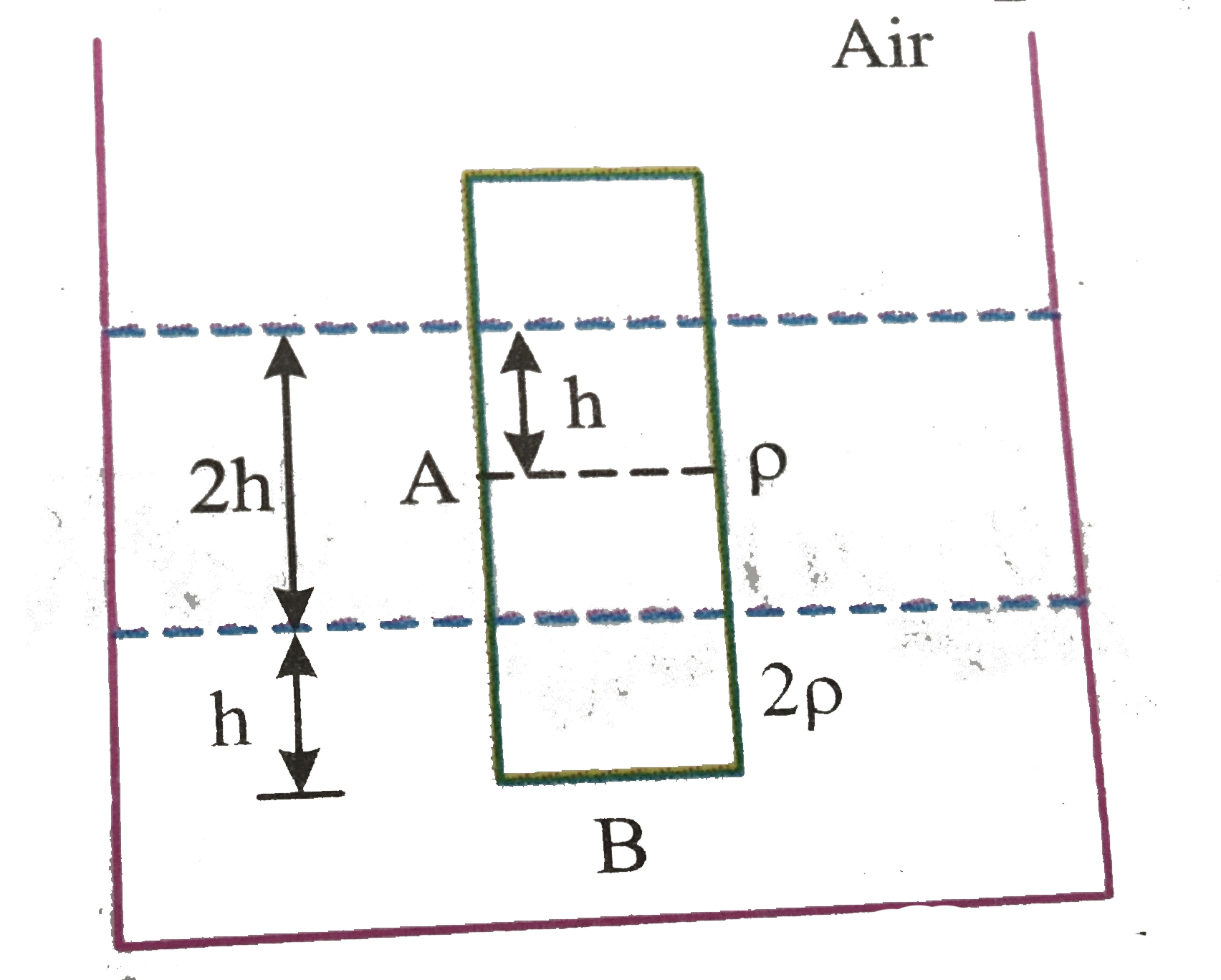
A cylinder stands vertical in two immiscible liquids of densities `rho` and `2rho` as shown. Find the difference in pressure at point A and B:01:59View Solution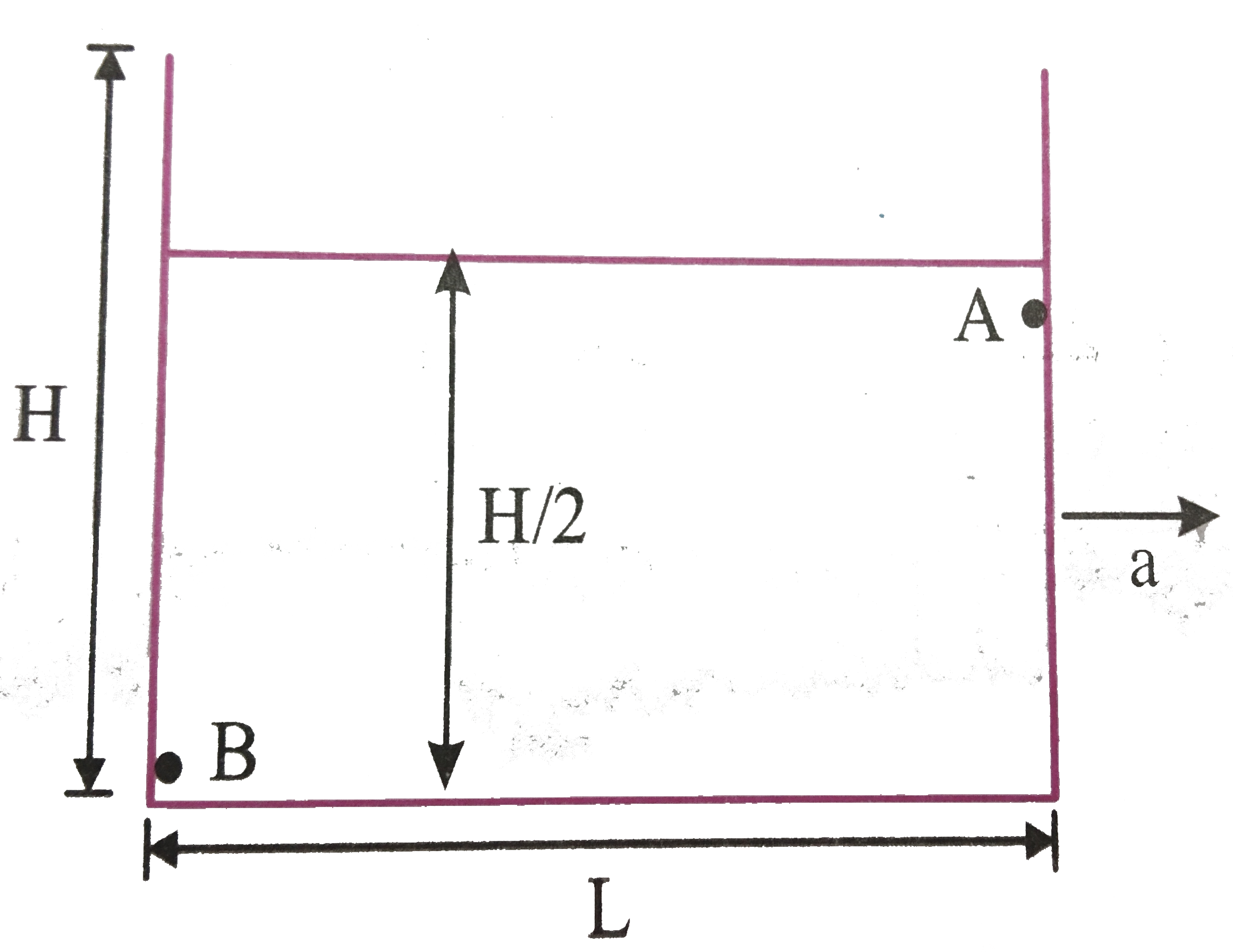
A vessel of height `H` and length `L` contains a liquid of density `rho` upto height `H//2` The vessel start accelerating horizontally with acceleration `a` towards right. If A is the point at the surface of the liquid at right . If A is the point at the surface of the liquid at right end while the vessel is accelerating and B is the point at bottom of the vessel on the other end, the difference of pressures at B and A will be03:14View Solution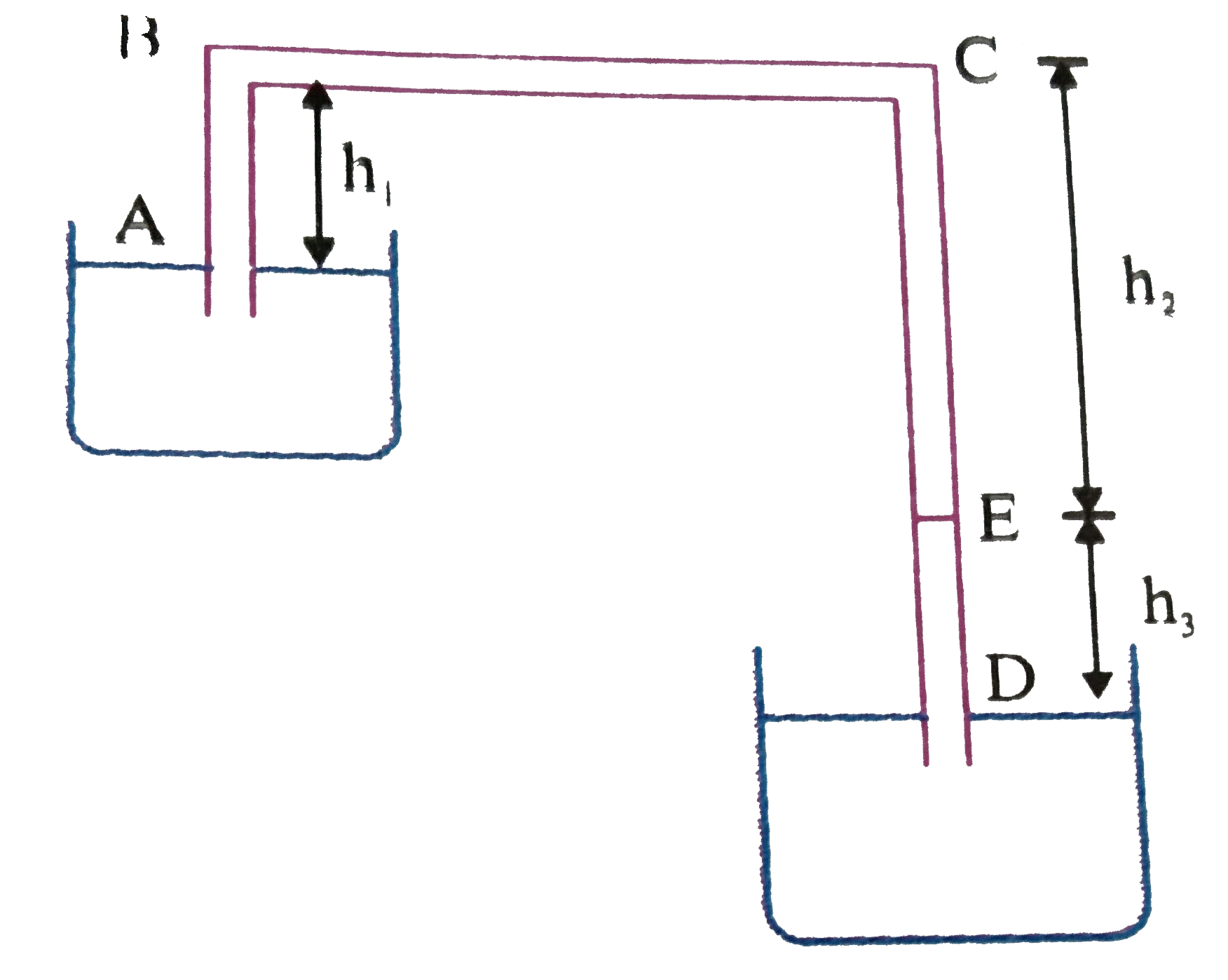
In the syphon as shown which of the option is not correct, if `h_(2)gth_(1)` and `h_(3)lth_(1)`?02:35View SolutionEqual volume of two immiscible liquids of densities `rho` and `2rho` are filled in a vessel as shown in the figure. Two small holes are punched at depths `h//2` and `3h//2` from the surface of lighter liquid. If `v_(1)` and `v_(2)` are the velocities of efflux at these two holes, then `v_(1)//v_(2)` is
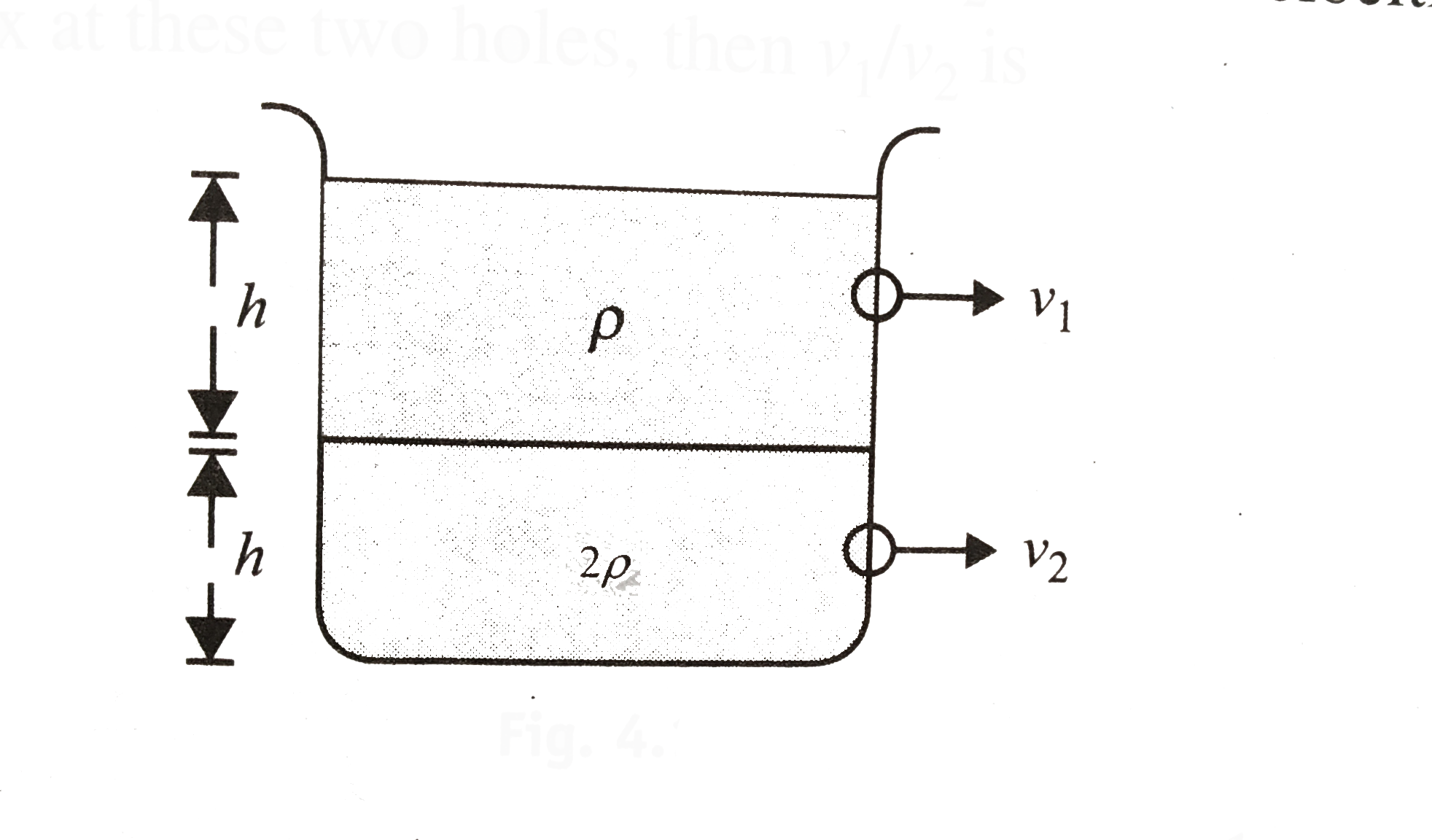 06:05View Solution
06:05View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities `2rho` and `rho` as shown in the figure is
 06:02View Solution
06:02View Solution
The fig shows a semo-cylinderical massless gate of unit length perpendicular to the plane of the page and is pivoted at the point `O` holding a stationary liquid of density `rho`. A horizontal foce `F` is applied at its lowest position to keep it stationary. The magnitude of the force is:05:14View SolutionA wooden block is floating in a water tank. The block is pressed to its bottom. During this process, work done is equal to :
02:20View SolutionA sphere of solid material of specific gravity `8` has a concentric spherical cavity and just sinks in water. The ratio of radius of cavity to that of outer radius of the sphere must be
04:58View SolutionA cylindrical tank of height `H` is open at the top end and it has a radius `r`. Water is filled in it up to a height of `h`. The time taken to empty the tank through a hole of radius `r'` in its bottom is
06:24View SolutionTwo unequal blocks placed over each other of densities `sigma_(1)` and `sigma_(2)` are immersed in a fluid of density of `sigma`. The block of density `sigma_(1)` is fully submerged so that ratio of their masses is `1/2` and `sigma//sigma_(1)=2` and `sigma//sigma_(2)=0.5`. Find the degree of submergence of the upper block of density `sigma_(2)`.
06:10View SolutionA thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If `rho_c` is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is
07:50View SolutionTwo balls of same size but different masses `m_(1)` and `m_(2)(m_(2)gtm_(1))` are attached to the two ends of a thin light thread and dropped from a certain height. It is known that the ciscous drag of air depends on the size and velocities of the balls. other than the gravitational pull from the earth and the viscous drag, the buoyant force from air also act on the balls, the buoyant force on a ball equals to the wweight of air displaced by the ball. After sufficiently long time from the instant the balls were dropped both of them acquire uniform velocity known as terminal velocity. When the balls have acquired terminal velocity, the tension in the thread is
02:55View Solution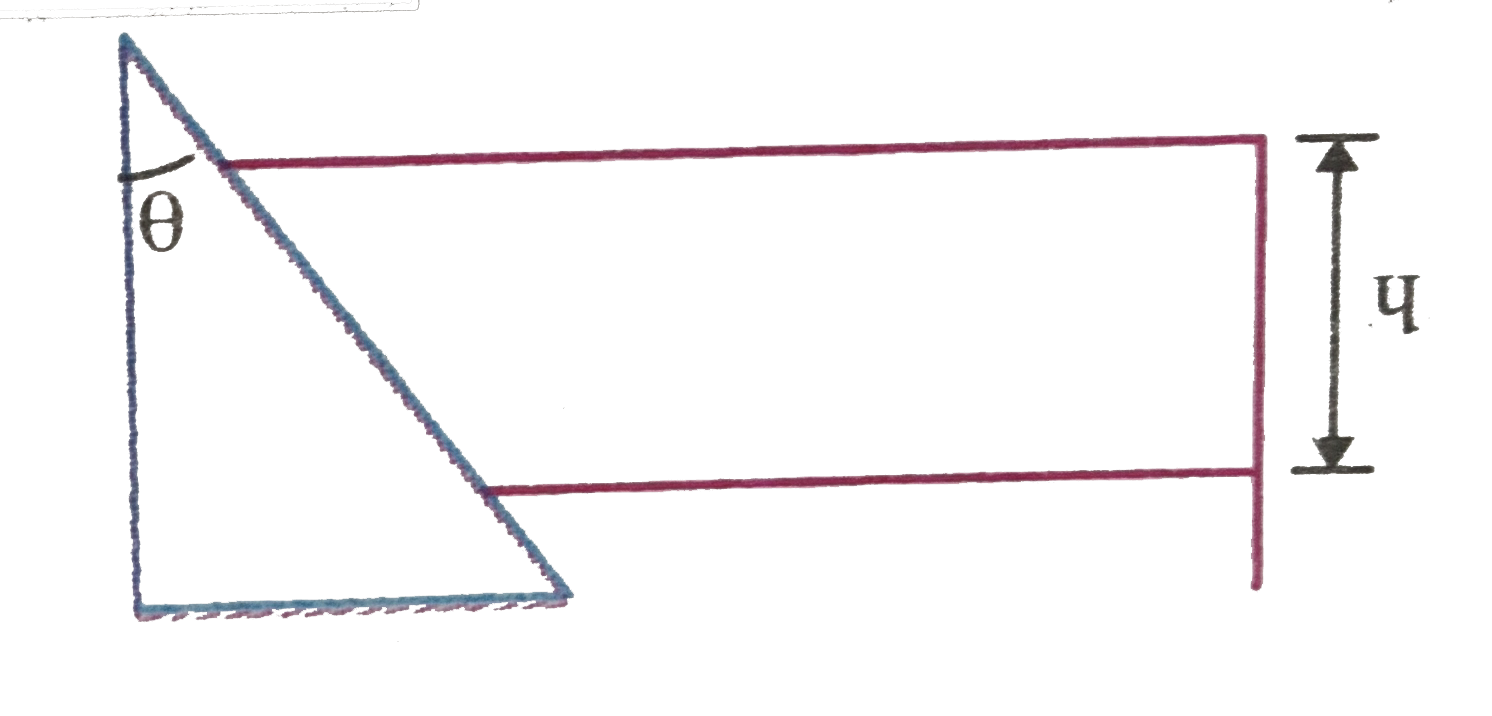
A silt is cut at the bottom, along the right bottom edge of a rectangular tank. The slit is closed by a wooden wedge of mass `m` and apex angle `theta` as shown in figure. The vertical plane surface of the wedge is in contact with the right vertical wall of the container. coefficient of static friction between these two surfaces is `mu`. To what maximum height can water be filled in the tank without leakage from the slit ? The width of tank is b and density of water is `rho`.04:11View Solution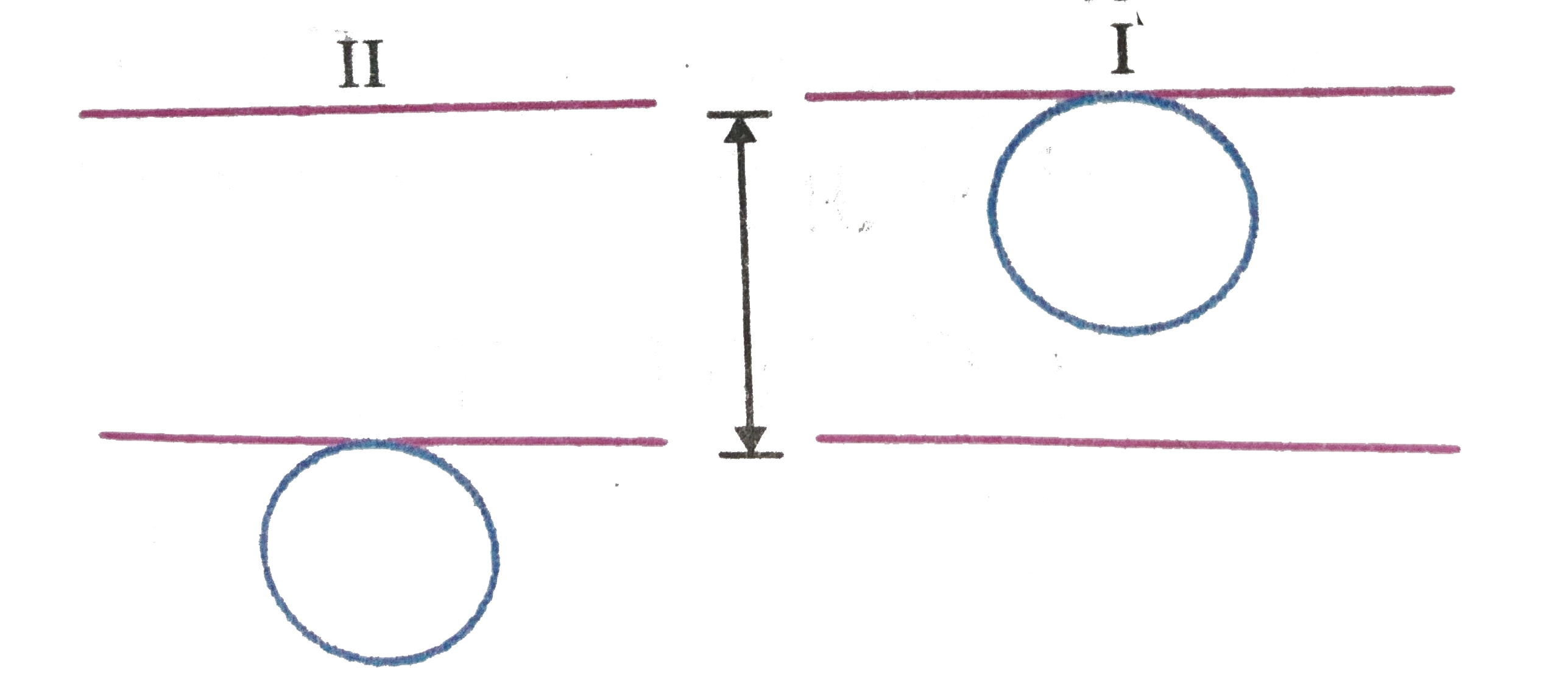
In figure-I is shown a sphere of mass `m` and radius `r` resting at the bottom of a large container filled with water. Depth of the container is `h`. Density of material of the sphere is the same as that of water. Now hte whole sphere is slowly pulled out of water as shown in figure-II Work done by the agent in pulling the sphere is equal to04:45View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities `d_1 and d_2` are filled in the tube. Each liquid subtends `90^@` angle at centre. Radius joining their interface make an angle `alpha` with vertical. Ratio `(d_1)/(d_2)` is :
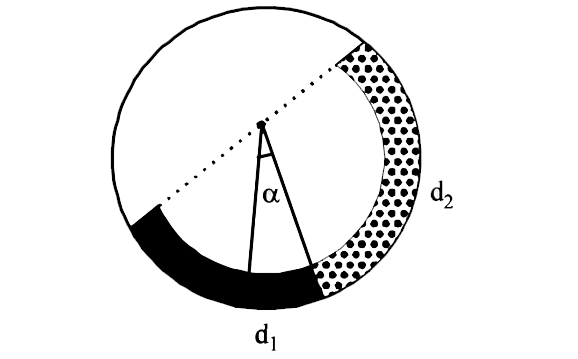 04:11View Solution
04:11View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure `P_0`. Then density D of solid is given by
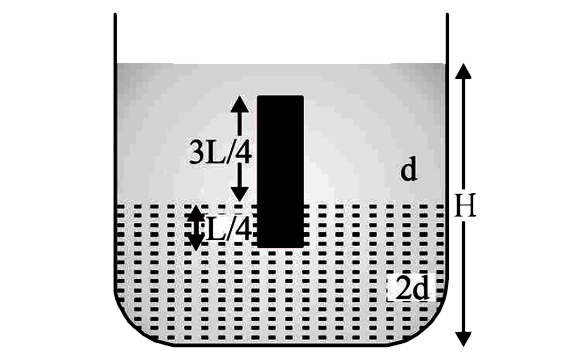 03:29View Solution
03:29View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle `theta` that the plank makes with the vertical in the equilibrium position. (Exclude the case `theta=theta^@`)
 09:25View Solution
09:25View SolutionA boat floating in a water tank is carrying a number of large stones. If the stones are unloaded into water, what will happen to the water level?
03:04View SolutionConsider a horizontally oriented syringe containing water located of a height of `1.25 m` above the ground. The diameter of plunger is `8 mm` and the diameter if the nozzle is `2 mm`. The plunger is pushed with a constant speed of `0.25 m//s`. Find the horizontal range of water stream on the ground. Take `g = 10 m//s^2`.
 .04:22View Solution
.04:22View Solution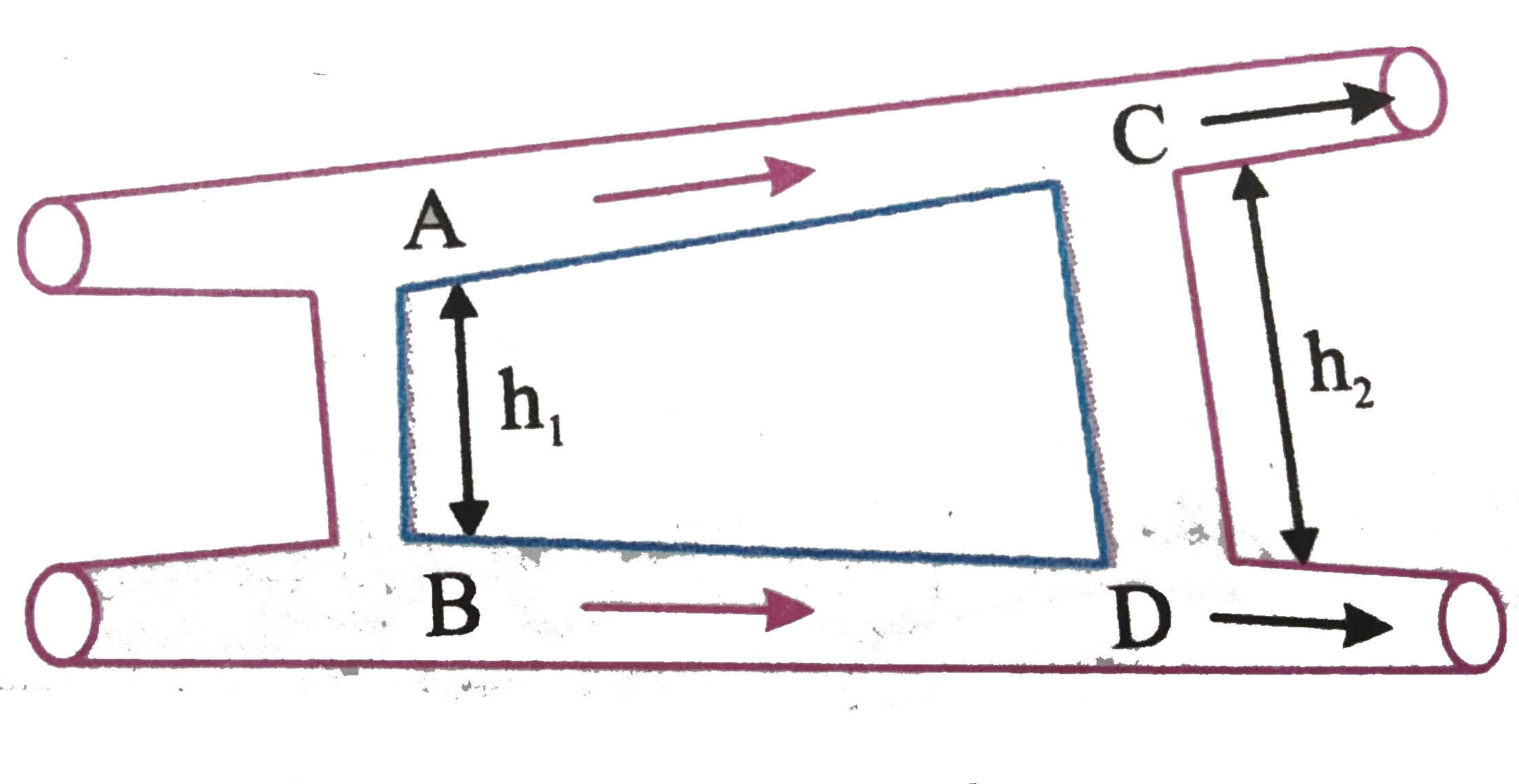
An ideal liquid is flowing in two pipes, AC is inclined and BD is horizontal. Both the pipes are connected by two vertical tubes of length `h_(1)` and `h_(2)` as shown in the fig. The flow is streamline in both the pipes. if velocity of liquid at A, B and C are `2m//s, 4m//s` and `4m//s` respectively, the velocity at D will be04:42View Solution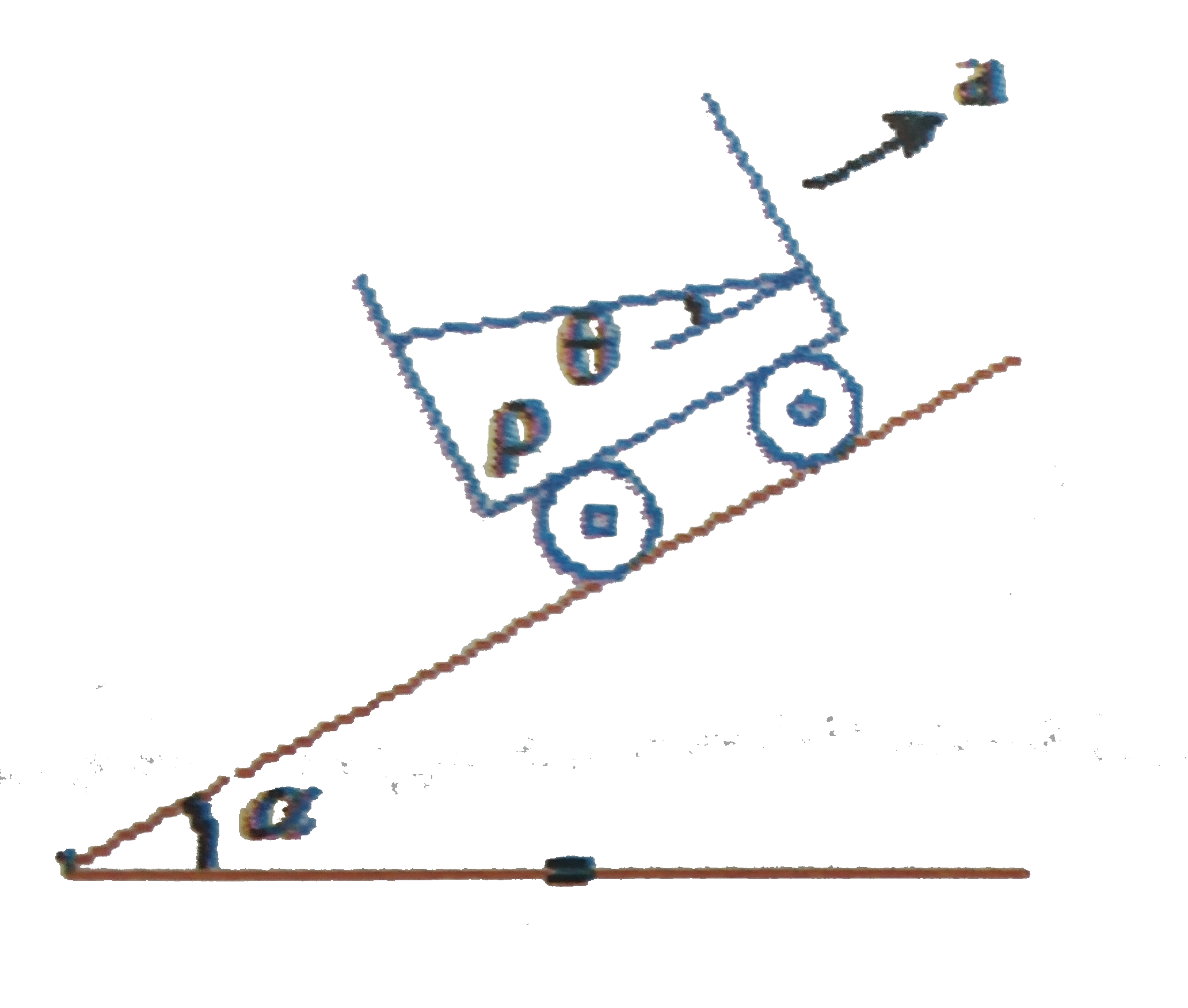
A fluid container is containing a liquid of density `rho` is accelerating upward with acceleration a along the inclined plane of inclination `alpha` as shown in the figure. Then the angle of inclination `theta` of free surface is03:34View Solution
Cylindrical block of area of cross-section A and of material of density `rho` is placed in a liquid of density one third of density of block. The block compress in the spring is one-third of te length of the block. if acceleration due to gravity is g, the spring constant of the spring is02:08View SolutionA cubic block of side a is connected with two similar vertical springs as shown. Initially, bottom surface of the block of density `sigma` touches the surface of the fluid of density `2sigma` while floating. A weight is placed on the block so that it is immersed half in the fluid, find the weight.
 06:59View Solution
06:59View Solution
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)02:34View SolutionA wooden stick of length `L`, radius `R` and density `rho` has a small metal piece of mass `m` ( of negligible volume) attached to its one end. Find the minimum value for the mass `m` (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density `sigma(gtrho)`.
09:39View Solution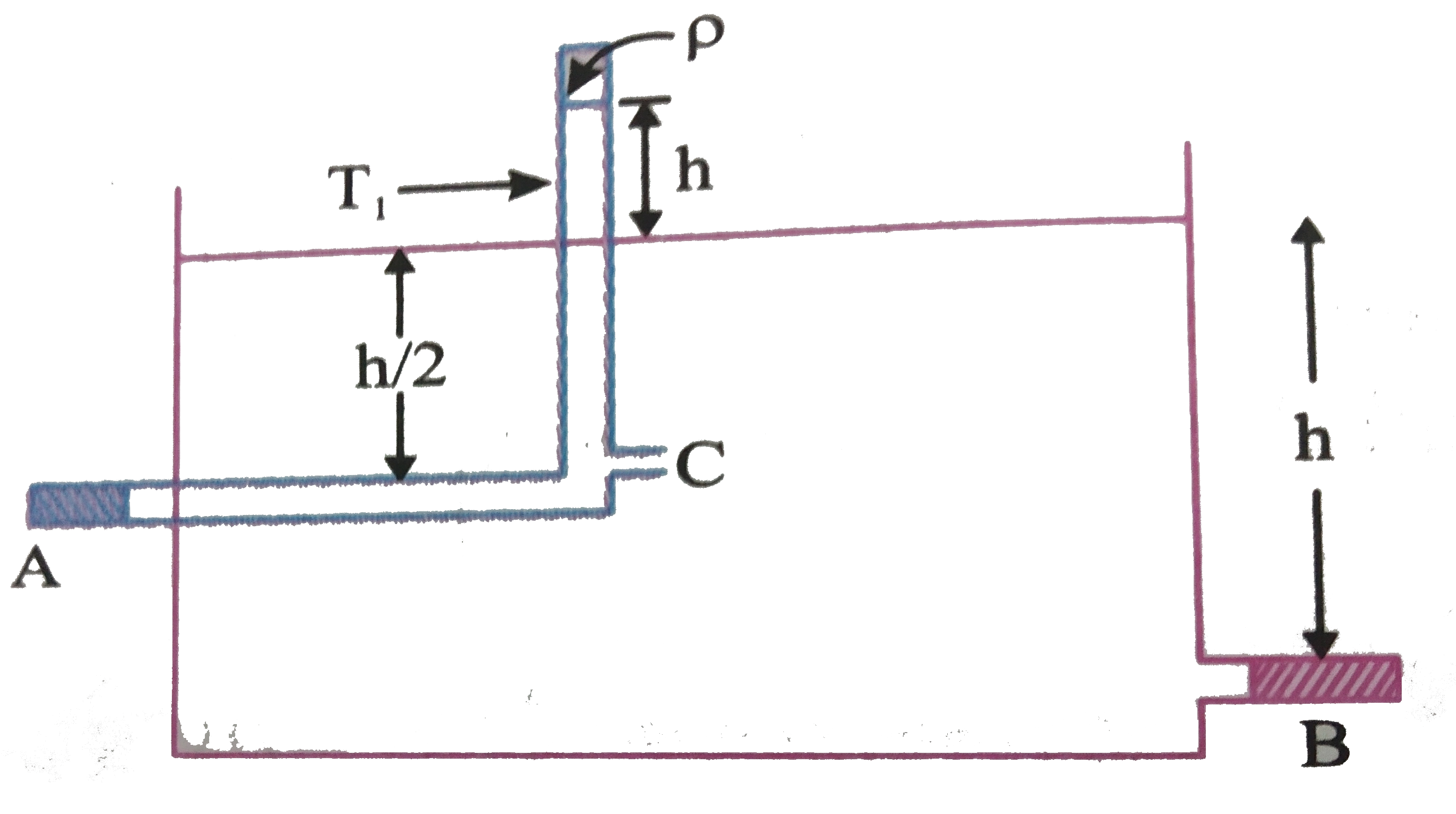
The cross-sectional areas of a tube `T_(1)` and the hole in the vessel at B are a and `a//2` respectively. There is a hole in the tube at C (at the level of A) through which liquid in the vessel rises by a height h in the tube. The other liquid heights are shown in the diagram. The plugs at A and B are removed simultaneously. How much horizontal force is required to keep vessel in equilibrium if p is the pressure in the tube and `p_(0)` is the atmospheric pressure? Hole C is closed when plugs are removed.03:21View SolutionA large open tank has two holes in the wall. The top hole is a square hole of side L at a depth y from the surface of water. The bottom hole is a circular hole of radius R at a depth 4y from surface of water . If `R=L//2 sqrt(pi)`, find the correct graph. `V_(1)` and `V_(2)` are the velocities in top and bottom holes. Area of the square & curcular holes are `a_(1)` and `a_(2)`
04:26View Solution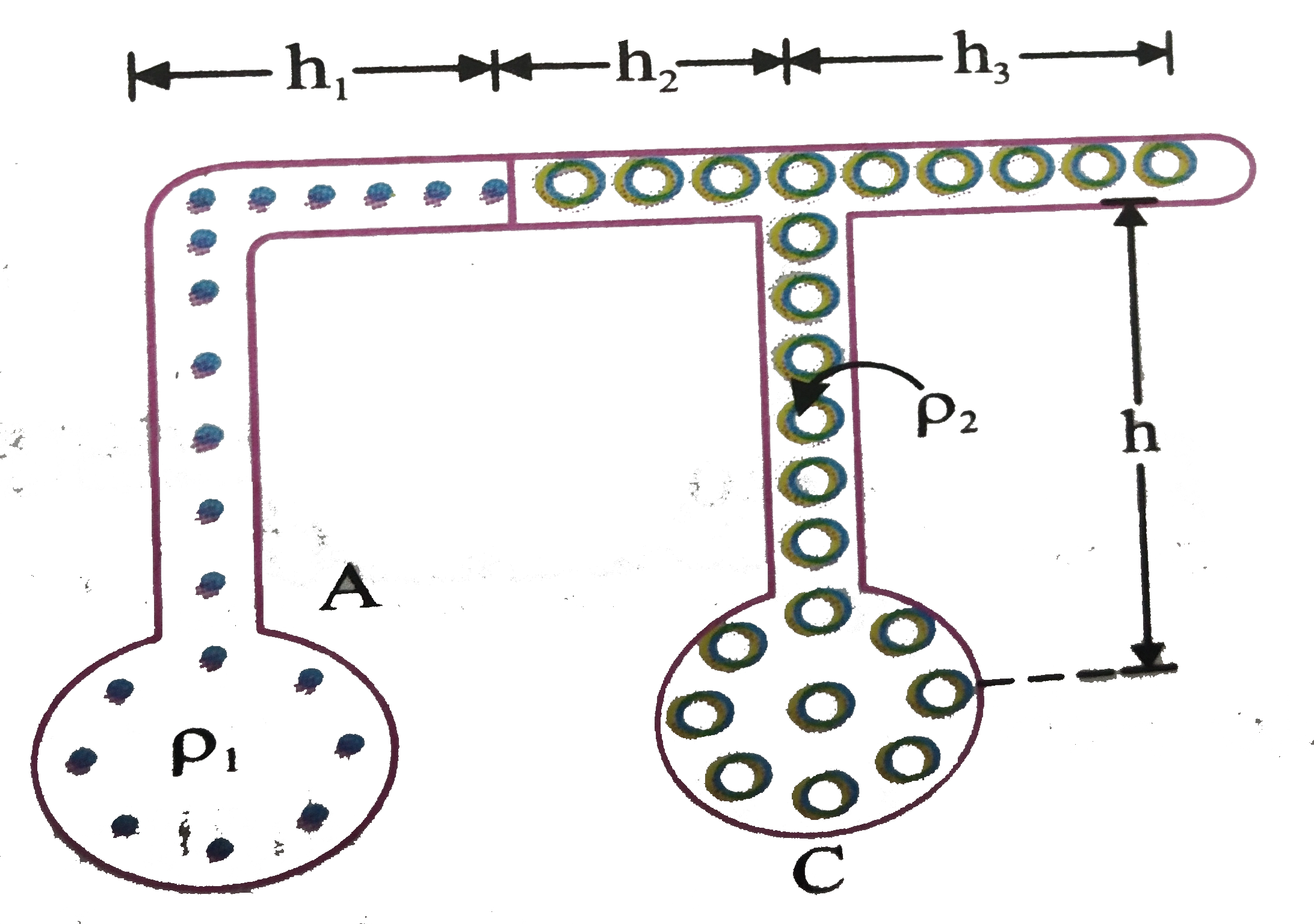
The difference in pressures in bulbs A and C having fluids of densities `rho_(1)` and `rho_(2)` when tube B is horizontal will be01:14View SolutionIn the arrangement as shown, `m_(B)=3m`, density of liquid is `rho` and density of block `B` is `2rho`. The system is released from rest so that block `B` moves up when in liquid and moves down when out of liquid with the same acceleration. Find the mass of block `A`.
 06:49View Solution
06:49View Solution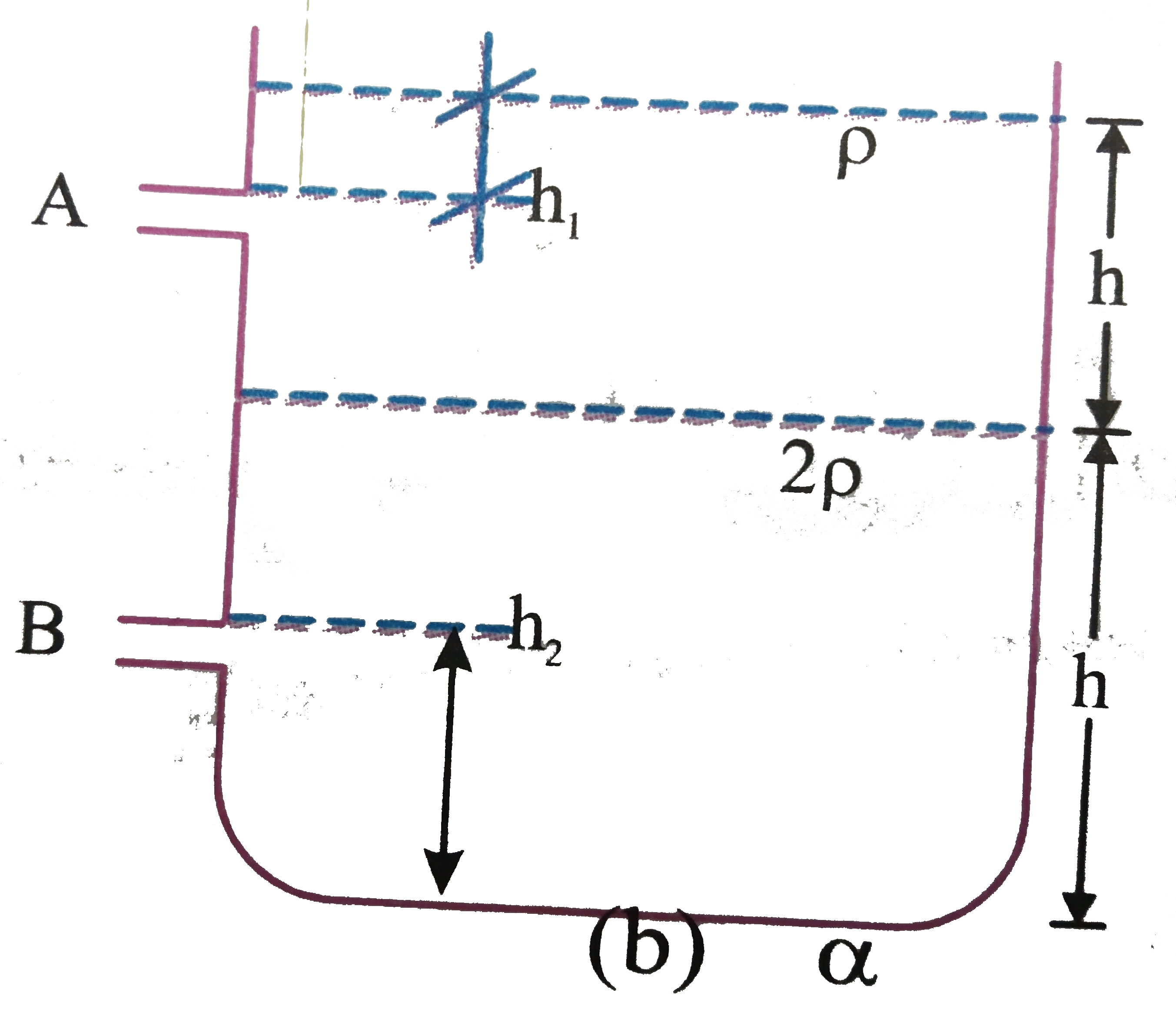
In the arrangement shown two liquids of density `rho` and `2rho` are filled in a container the height of both liquids is h. there are two holes A and B at heights `h_(1)` and `h_(2)` from top liquid surface and bottom of the vessel. if `V_(1)` and `V_(2)` are the velocities of efflux at the two holes A and B respectively, find the correct graph.
Take `=alpha((V_(2))/(V_(1)))^(2)`02:43View Solution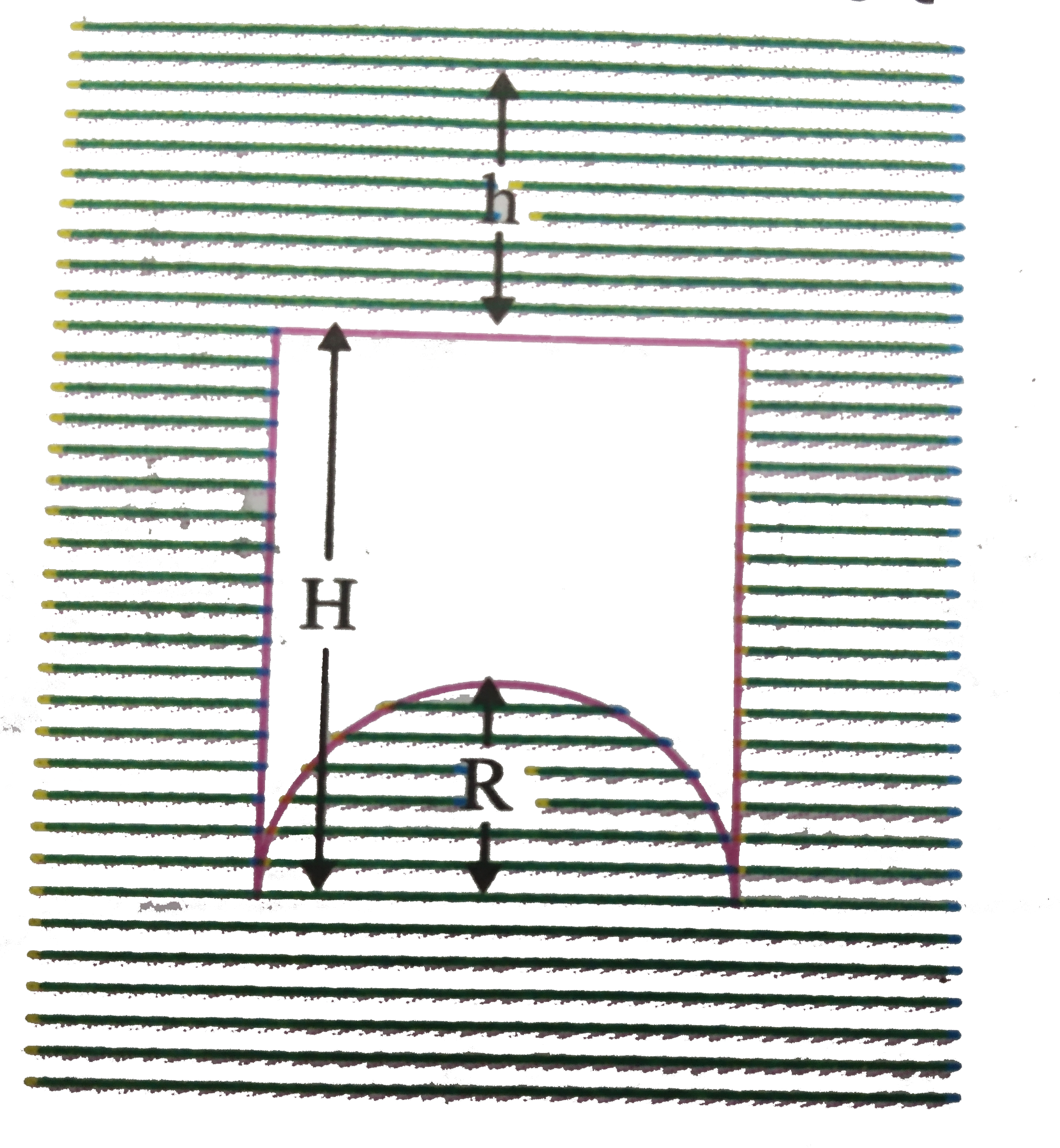
A cylinder of radius R, height H and density `simga` has a hemispherical cut at its bottom. The top of the cyliner is kept at depth h from the liquid surface. If the density of liquid is `rho`, find the hydrostatic force acting on the hemispherical surface of the cylinder.02:51View SolutionA cylindrical container of radius `'R'` and height `'h'` is completely filled with a liquid. Two horizontal `L`-shaped pipes of small cross-sectional area `'a'` are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is
 05:23View Solution
05:23View SolutionA marble of mass `x` and diameter `2r` is gently released in a tall cylinder containing honey. If the marble displaces mass `y(ltx)`of the liquid, then the terminal velocity is proportional to
05:21View SolutionA small metal ball of diameter `4 mm` and density `10.5 g//cm^(3)` in dropped in glycerine of density `1.5 g//cm^(3)`. The ball attains a terminal velocity of `8cm s^(-1)`. The coefficient of viscosity of glycerine is
03:56View SolutionA sphere of brass released in a long liquid column attains a terminal speed `v_(0)`. If the terminal speed attained by a sphere of marble of the same radius and released in the same liquid is `nv_(0)`, then the value of `n` will be (Given: The specific gravities of brass, marble and liquid are `8.5, 2.5` and `0.8`, respectively)
03:36View SolutionBetween a plate of area `100 cm^(2)` and another plate of area `100 m^(2)` there is a `1 mm`, thick layer of water, if the coefficient of viscosity of water is `0.01` poise, then the force required to move the smaller plate with a velocity `10 cms^(-1)` with reference to large plate is
03:37View SolutionA spherical ball falls through a viscous medium with terminal velocity `v`. If this ball is replaced by another ball of the same mass but half the radius, then the terminal velocity will be (neglect the effect of buoyancy.)
05:33View SolutionNeglecting the density of air, the terminal velocity obtained by a raindrop of radius `0.3 mm` falling through the air of viscosity `1.8 xx10^(-5) N//m^(2)` will be
03:36View SolutionWater is flowing in a river. If the velocity of a layer at a distance of 10 cm from the bottom is `20(cm)/(s)`. Find the velocity of layer at a height of `40cm` from the bottom
03:26View SolutionA horizontal plate `(10cmxx10cm)` moves on a layer of oil of thickness 4 mm with constant speed of `10(cm)/(s)`. The coefficient of viscosity of oil is 4 poise. The tangential force applied on the plate to maintain the constant speed of the plate is
03:22View SolutionA liquid is flowing through a narrow tube. The coefficient of viscosity of liquid is 0.1308 poise. The length and inner radius of tube are 50 cm and 1 mm respectively. The rate of flow of liquid is `360(cm^(3))/(min)`. Find the pressure difference between ends of tube.
03:14View SolutionFind the terminal velocity of solid sphere of radius 0.1 m moving in air in vertically downward direction. `(eta=1.8xx10^(-5)(Ns)/(m^(2))`, density of sphere `=1000(kg)/(m^(3))` and `g=10(m)/(s^(2)))`
02:41View SolutionEight equal drops of water each of radius `r=2mm` are falling through air with a terminal velocity of `16(cm)/(s)`. The eight drops combine to form a big drop. Calculate the terminal velocity of big drop.
03:04View SolutionAt `20^(@)C` to attain the terminal velocity how fast will an aluminium sphere of radil 1 mm fall through water. Assume flow to be laminar flow and specific gravity of `Al=2.5`
02:48View SolutionWater flows at a speed of 6 `cms^-1` through a tube of radius 1 cm. coefficient of viscosity of water at room temperature is 0.01 poise. Calculate the Reynolds number. Is it a steady flow.
01:44View SolutionA metal sphere of radius 1 mm and mass 50 mg falls vertically in glycerine. Find (a) the viscous force exerted by the glycerine on the sphere when the speed of the sphere is 1 cm s-1, (b) the hydrostatic force exerted by the glycerine on the sphere and (c) the terminal velocity with which the sphere will move down without acceleration. Density of glycerine `=1260kgm^-3` and its coefficient of viscosity at room temperature = 8.0 poise.
11:59View Solution
A liquid of density `900(kg)/(m^(3))` is filled in a cylindrical tank of upper radius 0.9 m and lower radius 0.3 m A capillary tube of length 1 is attached at the bottom of the tank as shown in fig. The capillary has outer radius 0.002 m and inner radius a. When pressure P is applied at the top of the tank volume flow rate of liquid is `8xx10^(-6)(m^(3))/(s)` and if capillary tube is detached, the liquid comes out from the tank with a velocity `10(m)/(s)`. then the coefficient viscosity of liquid is `(pia^(2)=10^(-6)m^(2)a^(2))/(l=2xx10^(-6)m)`.10:00View SolutionIf the terminal speed of a sphere of gold (density `=19.5kg//m^3`) is `0.2m//s` in a viscous liquid (density `=1.5kg//m^3`), find the terminal speed of a sphere of silver (density `=10.5kg//m^3`) of the same size in the same liquid
03:08View SolutionA cylindrical vessel of area of cross-section A and filled with liquid to a height of `h_(1)` has a capillary tube of length l and radius r protuding horizontally at its bottom. If the viscosity of liquyid is `eta` and density `rho`. Find the time in which the level of water in the vessel falls to `h_(2)`.
06:17View SolutionWhen water flows through a tube of radius r placed horizontally, a pressure difference p develops across the ends of the tube. If the radius fo the tube is doubled and the rate fo flow halved, the pressure differnece will be
03:09View SolutionA spherical solild of volume V is made of a material of density `rho_(1)`. It is falling through a liquid of density `rho_(2)(rho_(2) lt rho_(1))`. Assume that the liquid applies a viscous froce on the ball that is proportional ti the its speed v, i.e., `F_(viscous)=-kv^(2)(kgt0)`. The terminal speed of the ball is
01:56View SolutionA volume V of a viscous liquid flows per unit time due to a pressure head `DeltaP` along a pipe of diameter d and length l. instead of this pipe a set of four pipes each of diameter `(d)/(2)` and length 2l is connected to the same pressure head `DeltaP`. Now the volume of liquid flowing per unit time is:
04:41View SolutionTwo capillary tubes of same radius `r` but of lengths `l_(1)` and `l_(2)` are fitted in parallel to the bottom of a vessel. The pressure to the bottom of a vessel. The pressure head is P. What should be the length of a singl tube of same radius that can replace the two tubes so that the rate of flow is same as before?
04:00View Solution`L,(L)/(2)` and `(L)/(3)` are connected in series. Their radii are r, `(r)/(2)` and `(r)/(3)` respectively. Then, if stream-line flow is to be maintained and the pressure across the first capillary is P, then:
04:31View SolutionFind the maximum possible mass of a greased needle floating on water surface.
03:38View SolutionA vertical capillary tube with inside diameter `0.50 mm` is submerged into water so that the length of its part emerging outside the water surface is equal to `25 mm`. Find the radius of curvature of the meniscus. Surface tension of water is `73xx10^(-3)N//m`.
04:13View Solution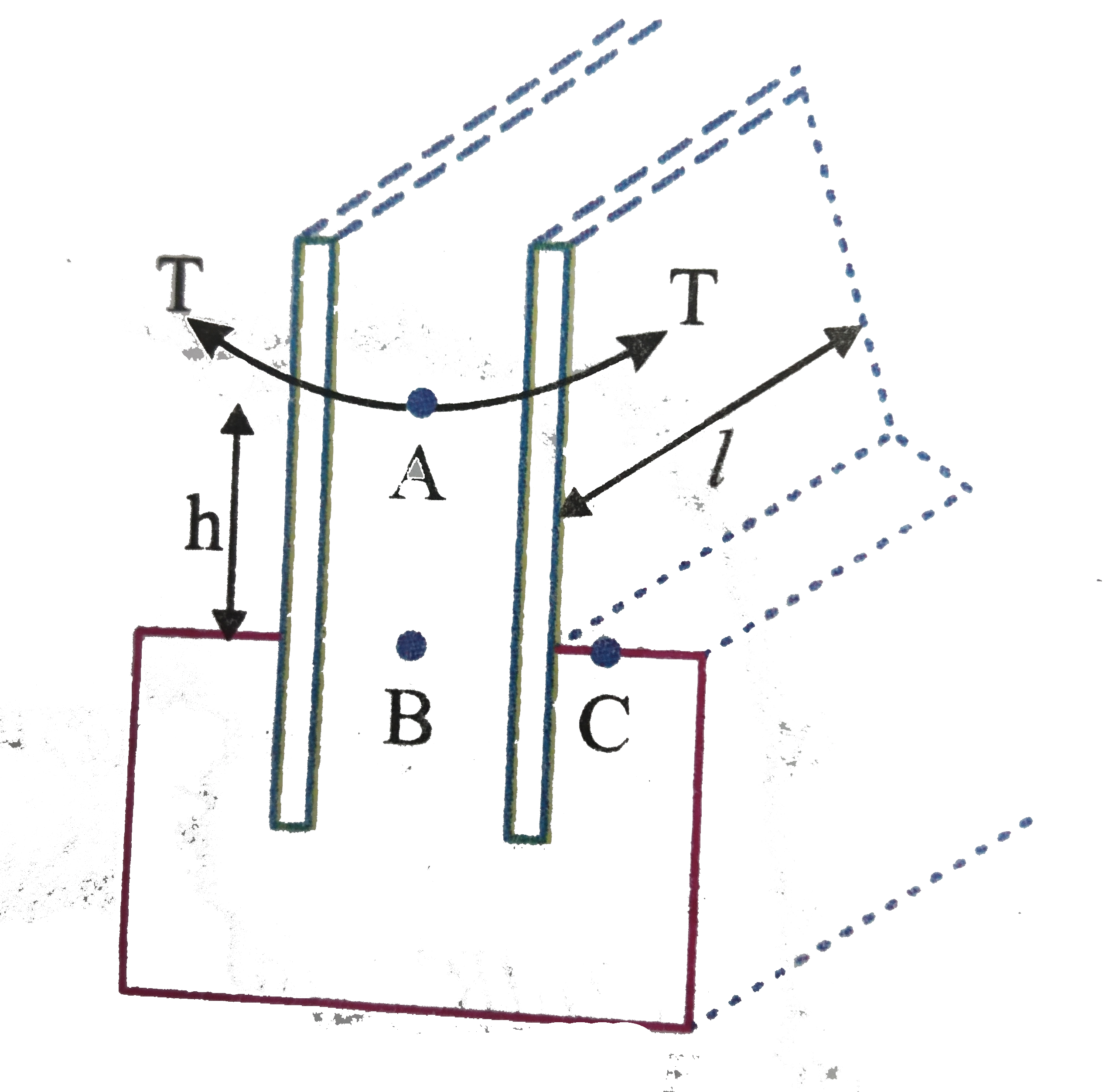
Expression for the height of capillary rise between two parallel plates dipping liquid of density `sigma` separated by a distance d. The surface tension of the liquid is T. [Take angle of contact to be zero]03:24View SolutionA glass capillary sealed at the upper end is of length `0.11 m` and internal diameter `2xx10^(5)`m. The tube is immersed vertically into a liquid of surface tension `5.06xx10^(-2)N//m`. To what length the capillary has to be immersed so that the liquid level inside and outside the capillary becomes the same. What will happen to water level inside the capillary if the seal is now broken?
07:49View Solution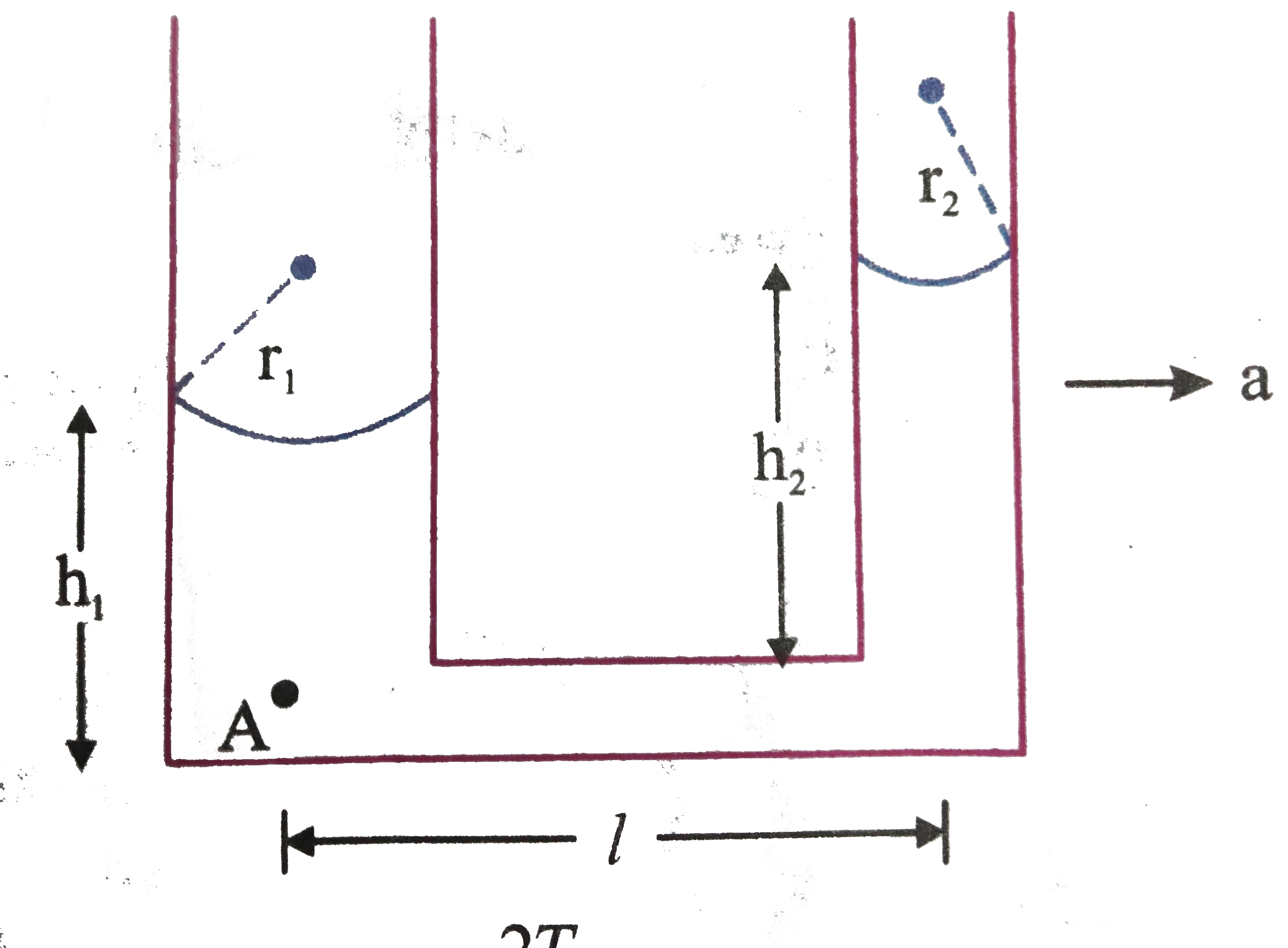
A vertical communicating tube contains a liquid of density `rho`. If it moves with a horizontal acceleration `a`, pressure at `A` is equal to :02:56View SolutionA glass rod of diameter `d=2mm` is inserted symmetrically into a glass capillary tube of radius `r=2mm`. Then the whole arrangement is vertically dipped into liquid having surface tension 0.072 Nm. The height to which liquid will rise on capillary is (Take `g=10(m)/(s^(2))`, `"density"_("liq")=1000(kg)/(m^(3)))`. Assume contact angle to be zero, capillary tube to be long enough
06:08View Solution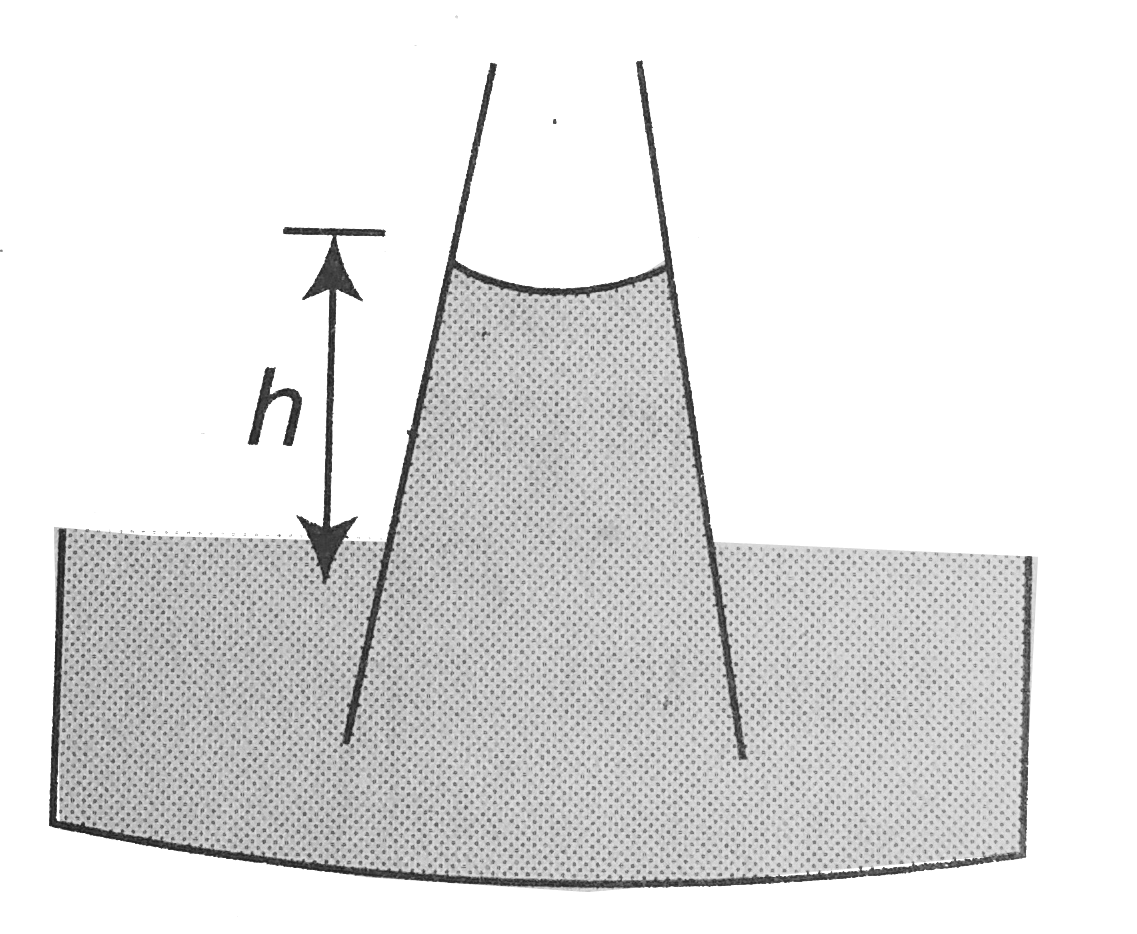
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is `0^@` and effect of liquid inside the mexiscus is to be neglected. `T` is surface tension of the liquid, `r` is radius of the meniscus, `g` is acceleration due to gravity and `rho` is density of the liquid then height `h` in equilibrium is:01:39View SolutionIn the bottom of a vessel with mercury there is a round hole of diameter `d=70mum`. At what maximum thickness of the mercury Layer will the liquid still not flow out through this hole ? `[rho_("mercury")=13600(kg)/(m^(3))]`
04:31View SolutionAn air bubble of diameter `d=4mum` is located in water at a depth `h=5.0m` considering standard atmospheric pressure at 1 atm, find the pressure in the air-bubble?
02:54View SolutionWater rises to a height of `10 cm` in a capillary tube and mercury falls to a depth of `3.42 cm` in the same capillary tube. If the density of mercury is `13.6 g//c.c.` and the angles of contact for mercury and for water are `135^@` and `0^@`, respectively, the ratio of surface tension for water and mercury is
04:54View SolutionA glass rod of radius `r_(1)` is inserted symmetrically into a vertical capillary tube of radius `r_(2)` such that their lower ends are at the same level. The arrangement is now dipped in water. The height to which water will rise into the tube will be (`sigma =` surface tension of water, `rho = ` density of water)
06:18View SolutionA large number of droplets, each of radius a, coalesce to form a bigger drop of radius `b`. Assume that the energy released in the process is converted into the kinetic energy of the drop. The velocity of the drop is `sigma =` surface tension, `rho =` density)
07:52View SolutionTwo glass plates are separated by water. If surface tension of water is `75 dyn//cm` and the area of each plate wetted by water is `8 cm^(2)` and the distance between the plates is `0.12 mm`, then the force applied to separate the two plates is
05:09View SolutionThe lower end of a capillary tube is at a depth of `12 cm` and water rises `3 cm` in it. The mouth pressure required to blow an air bubble at the lower end will be `x cm` of water column, where `x` is
03:13View SolutionA light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution `=25 dyn cm^-1`. Take g=10 ms^-2`
 05:36View Solution
05:36View SolutionThe angle of contact between glass and water is `0^@` and surface tension is `70 dyn//cm`. Water rises in a glass capillary up to `6 cm`. Another liquid of surface tension `140 dyn//cm`, angle of contact `60^@` and relative density `2` will rise in the same capillary up to
04:25View SolutionWork `W` is required to form a bubble of volume `V` from a given solution. What amount of work is required to be done to form a bubble of volume `2V` ?
03:50View SolutionTwo vertical parallel glass plates are partially submerged in water. The distance between the plates is d and the length is `l`. Assume that the water between the plates does not reach the upper edges of the plates and the wetting is complete. The water will rise to height (`rho=` density of water and `alpha =` surface tension of water)
04:56View SolutionA drop of Volume `V` is pressed between the two glass plates so as to spread to an area of `A`. If `T` is the surface tension, the normal force required to separate the glass plates is
03:07View SolutionA glass capillary tube is of the shape of a truncated cone with an apex angle `alpha` so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if `rho`, and its contact angle with glass is `theta`, the value of h will be (g is the acceleration due to gravity)
 09:08View Solution
09:08View SolutionOn heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If `rlt ltR` and the surface tension of water is T, value of r just before bubbles detach is: (density of water is `rho_w`)
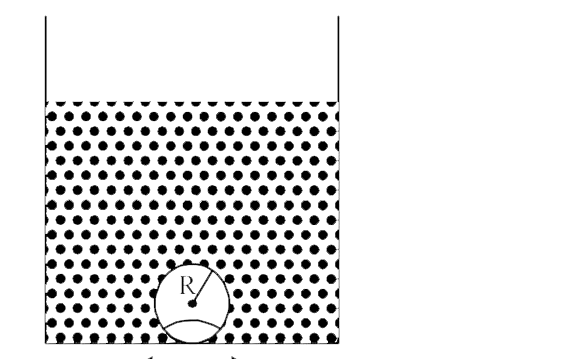 05:58View Solution
05:58View SolutionAssume that a drop of liquid evaporates by decreases in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is `rho` and L is its latent heat of vaporization.
08:15View SolutionA glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
 02:13View Solution
02:13View SolutionA vessel filled with air under pressure `p_(0)` contains a soap bubble of diameter `d`. The air pressure have been reduced `n`-fold, and the bubble diameter increased `r`-fold is isothermally. Find the surface tension of the soap water solution.
05:15View SolutionThe high domes of ancient buildings have structural value (besides beauty). It arises from pressure difference on the 2 faces due to curvature (as in soap bubbles). There is a dome of radius 5 m and uniform (but small ) thickness. The surface tension of its masonry structure is about 500 N/m. Treated as hemispherical, the maximum load that the dome can support is nearest to
03:02View SolutionA barometer contains two uniform capillaries of radii `1.4xx10^(-3)m` and `7.2xx10^(-4)m`. If the height of liquid in narrow tube is `0.2m` more than that in wide tube, calculate the true pressure difference. Density of liquid `=10^(3)kg//m^(3)`, surface tension `=72xx10^(-3)N//m` and `g=9.8ms^(-12)`.
07:06View Solution
Single Answer Questions questions and complete solutions for chapter MECHANICAL PROPERTIES OF FLUIDS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- C.U.Q
- C.U.Q (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM)
- C.U.Q (TORRICELLI.S THEOREM AND VISCOSITY)
- C.U.Q(POISEUILLE.S EQUATION)
- C.U.Q(PRESSURE, FORCE OF BUOYANCY, LAWS OF FLOATATION)
- Comprehension Type Questions
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 10
- EVALUATE YOURSELF - 11
- EVALUATE YOURSELF - 12
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EVALUATE YOURSELF - 5
- EVALUATE YOURSELF - 6
- EVALUATE YOURSELF - 7
- EVALUATE YOURSELF - 8
- EVALUATE YOURSELF - 9
- Examples
- EXERCISE - I - (C.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - I - (C.W) (COEFFICIENTY OF VISCOSITY & VISCOUS FORCE)
- EXERCISE - I - (C.W) (COMBINATION OF DROPS & BUBBLES)
- EXERCISE - I - (C.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND APPLICATIONS)
- EXERCISE - I - (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND SOAP BUBBLE)
- EXERCISE - I - (C.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - I - (C.W) (POISEUILLE.S EQUATION)
- EXERCISE - I - (C.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - I - (C.W) (TERMINAL VELOCITY & VISCOUS FORCE)
- EXERCISE - I - (C.W) (TORRICELLI.S THEOREM)
- EXERCISE - I - (H.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - I - (H.W) (COEFFICIENT OF VISCOSITY & VISCOUS FORCE)
- EXERCISE - I - (H.W) (COMBINATION OF DROPS & BUBBLES)
- EXERCISE - I - (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - I - (H.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND SOAP BUBBLE)
- EXERCISE - I - (H.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - I - (H.W) (POISEUILLE.S EQUATION)
- EXERCISE - I - (H.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - I - (H.W) (REYNOLDS NUMBER)
- EXERCISE - I - (H.W) (TERMINAL VELOCITY)
- EXERCISE - I - (H.W) (TORRICELLI.S THEOREM)
- EXERCISE - I - (H.W) (VARIATION OF PRESSURE, UPTHRUST)
- EXERCISE - I - (H.W) (WORK & SURFACE ENERGY)
- EXERCISE - II (C.W) (CAPILLARITY & CAPILLARY RISE)
- EXERCISE - II (C.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - II (C.W) (EXCESS PRESSURE INSIDE A LIQUID DROP AND IN A SOAP BUBBLE)
- EXERCISE - II (C.W) (FORCE DUE TO SURFACE TENSION)
- EXERCISE - II (C.W) (POISEUILLE.S EQUATION)
- EXERCISE - II (C.W) (PRESSURE AND PASCAL.S LAW)
- EXERCISE - II (C.W) (TERMINAL VELOCITY)
- EXERCISE - II (C.W) (TORRICELLI.S THEOREM)
- EXERCISE - II (C.W) (VARIATION OF PRESSURE, UPTHRUST)
- EXERCISE - II (C.W) (WORK & SURFACE ENERGY)
- EXERCISE - II (H.W) (CAPILLARITY AND CAPILLARY RISE)
- EXERCISE - II (H.W) (EQUATION OF CONTINUITY, BERNOULLI.S THEOREM AND ITS APPLICATIONS)
- EXERCISE - II (H.W) (EXCESS PRESSURE IN A LIQUID DROP AND IN A SOAP BUBBLE
- EXERCISE - II (H.W) (POISEUILLE.S EQUATION)
- EXERCISE - II (H.W) (PORCE DUE TO SURFACE TENSION)
- EXERCISE - II (H.W) (TORRICELLI.S THEOREM)
- EXERCISE - II (H.W) (VARIATION OF PRESSURE AND UPTHRUST)
- EXERCISE - II (H.W) (WORK & SURFACE ENERGY)
- EXERCISE - III
- Illustration
- Level 1 (C.W)
- Level 1 (H.W)
- Level 2 (C.W)
- Level 2 (H.W)
- Level 3
- More Than One Alternative Type Question
- Paragraph Type Questions
- Single Answer Questions
- Statement Type Questions
