Complete Solutions to Exercise-I (H.W) of chapter WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVES |
| NARAYANA | Exercise-I (H.W) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Which of the following represents a progressive wave
View SolutionA longitudinal progressive wave is given by the equation `y=5x10^(-2)sinpi(400t+x)`. The amplitude and wave length of the wave are (y,x are in m)
View SolutionThe equation of a progressive wave is `y=0.05sin(200t-(x)/(2))` where x,y are in metres and t in seconds then
`(a)` velocity of wave is `100ms^(-1)`
`(b)` max velocity of particle is `10ms^(-1)`
`(c )` wavelength of wave is `4m`
View SolutionThe equation of a transverse wave is`y=asin2pi[t-(x//5)]` , then the ratio of maximum particle velocity and wave velocity is
View SolutionThe frequency of a tuning fork is `256Hz` . The velocity of sound in air is `344ms^(-1)`.The distance travelled (in metres) by the sound during the time in which the tuning fork completes `32`vibrations
View SolutionA progressive wave moves with a velocity of `36` m/s in a medium with a freqency of `200 Hz`. The phase difference between two particles separeted by a distance of `1 cm` is
View SolutionThe equation of a wave is `y=4sin{(pi)/(2)(2t+(x)/(8))}` where `y,x` are in cm and time in seconds . The acceleration of particle located at `x=8cm` and `t=1sec` is
View SolutionA standing wave set up in a medium is ` y=4cos((pix)/(3))sin40pit` where x,y are in cm and t in sec The velocity of medium perticle at `x=6cm` at `t=1//8`sec is
View SolutionA travelling wave pulse is given by `y = (10)/(5 + (x + 2t)^(2))`
Here, `x and y` are in meter and `t` in second. In which direction and with what velocity is the pulse propagation. What is the ampitude of pulse?
View SolutionA wave of angular frequency `30` rad//sec propagates so that a certain phase of oscillationn moves along x-axis, y-axis , z-axis with speeds `1m//s`, `2m//s` and `2m//s` respectively. The propagation constant `K` is
View SolutionThe situation of a wave pulse is given as `y=(0.8)/((4x+5t)+4)` the amplitude and velocity of pulse are
View SolutionA suspension bridge is to be built across valley where it is known that the wind can gust at `5`s intervals .It is estimated that the speed of transverse waves along the span of the bridge would be `400` m/s . The danger of resonant motions in the bridge at its fundamental frequency would be greater if the span had a length of
View SolutionA uniform rope of length `20`m and mass `5`kg is hanging vertically from a rigid support. A block of mass `4`kg is attached to the free end. The wave length of the transverse wave pulse at the lower end of the rope is `0.04` m. The wavelength of the same pulse as it reaches the top is
View SolutionA uniform rope of mass `0.1 kg` and length `2.45 m` hangs from a ceiling.
(a) Find the speed of transverse wave in the rope at a point `0.5 m` distant from the lower end.
(b) Calculate the time taken by a transverse wave to travel the full length of the rope.

View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x from the bottom is proportional to
View SolutionA string of length 10.0 m and mass 1.25kg stretched with a tension of 50N. If a transverse pulse is created at one end of the string, how long does it take to reach the other end ?
View SolutionThe linear density of a vibrating string is `1.3 xx 10^(-4) kg//m` A transverse wave is propagating on the string and is described by the equation `y= 0.021 sin (x + 30 t)` where x and y are measured in meter and t`t` in second the tension in the string is :-
View SolutionIn the given arrangement, if hanging mass will be changed by 4%, then percentage change in the wave speed in string will be:

View SolutionThe extension in a string, obeying Hooke's law is `x`. The speed of sound in the stretched string is `V`. If the extension in the string is increased to `2x` then speed of sound will be
View SolutionThe speed of transverse waves in a stretched string is `700cm//s`. If the string is `2m` long, the frequency with which it resonates in fundamental mode is
View SolutionTwo waves represented by `y= a" "sin(omegat-kx) and y=a" " sin(omegat-kx+(2pi)/(3))` are superposed. What will be the amplitude of the resultant wave?
View SolutionThe minimum phase difference between the two simple harmonic oscillations
`x_(1)=(1//2)sinomegat+(sqrt(3)//2)cosomegat and`
`x_(2)=(sqrt(3)//2)sinomegat+(1//2)cosomegat` is
View SolutionTwo waves of amplitudes `A_(0)` & `xA_(0)` pass through a region. If `x gt 1`, the difference in the maximum and minimum resultant amplitude possible it
View SolutionA pulse in a rope approaches a solid wall and it gets reflected from it
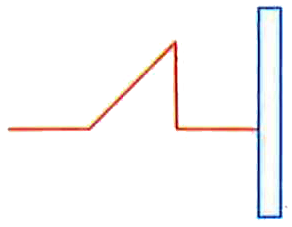
The wave pulse after reflection is best represented by
View SolutionA wave pulse on a string has the dimension at time `t=0` as shown below is reflected from a fixed end `O`.
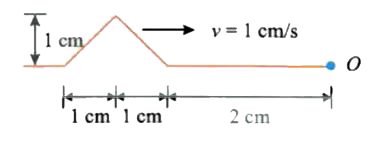
Its dimensions at `t=3s` is
View SolutionThe length of a sonometer wire is `90cm` and the stationary wave setup in the wire is represented by an equation `y=6sin((pix)/(30))cos(250t)` where `x` , `y` are in cm and `t` is in second. The distances of successive antinodes from one end of the wire are
View SolutionA sonometer consists of two wire of length , same material whose radii are in the ratio `2:3`. The ratio of tension in two wire if their fundamental freqencies are equal is
View SolutionThe bridge of a sonometer is slightly displaced so that the length of wire is decreased by `0.5%` and tension in the wire is increased by `1%`. The fundamental frequency of wire
View SolutionA segment of wire vibrates with a fundamental frequency of 450 Hz under a tension of 9Kg-wt.Then, tension at which the fundamental frequency of the same wire becomes 900 Hz is
View SolutionIn Melde's experiment, the string vibrates in 4 loops when a 50 gram weight is placed in the pan of weight 15 gram . To make the string to vibrates in 6 loops the weight that has to be removed from the pan is
View SolutionTwo vibrating strings of the same material but lengths `L` and `2L` have radii `2r` and `r` respectively. They are stretched under the same tension. Both the string vibrate in their fundamental nodes, the one of length `L` with freuqency `v_(1)` and the other with frequency `v_(2)`. the ratio `v_(1)//v_(2)` is given by
View Solutionv20
View SolutionTwo unifrom strectched strings A and B, made of steel, are vibrating under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is
View SolutionA string of length l along x-axis is fixed at both ends and is vibrating in second harmonic. If at `t=0`, `y=2.5mm` for incident wave, the equation of standing wave is (`T` is tension and `mu` is linear density)
View SolutionA steel wire of length `1m`, mass `0.1kg` and uniform cross-sectional area `10^(-6)m^(2)` is rigidly fixed at both ends. The temperature of the wire is lowered by `20^(@)C`. If transverse waves are set up by plucking the string in the middle.Calculate the frequency of the fundamental mode of vibration.
Given for steel `Y = 2 xx 10^(11)N//m^(2)`
`alpha = 1.21 xx 10^(-5) per ^(@)C`
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air `= 320 ms^-1`

View SolutionA sound wave of wavelength 32 cm enters the tube at S as shown in the figure. Then the smallest radius r so that a minimum of sound is heard at detector D is

View SolutionA sonometer wire with a suspended mass of M=1 kg is in resononce with a given tuning fork. The apparatus is taken to the moon where the acceleration due to gravity is `1//6^(th)` that on earth. To obtain resonance on the moon, the value of M should be
View SolutionA sonometer wire of length `L` is plucked at a distance `L//8` from one end then it vibrates with a minimum frequency `n`. If the same wire plucked at a distance `L//6` from another end the minimum frequency with which it vibrates is
View SolutionA metal wire of linear mass density of `9.8g//m` is stretched with a tension of `10 kg-wt` between two rigid support `1meter` apart. The wire passes at its middle point between the poles of a permanent magnet, and it vibrates in resonance when carrying an alternating current of frequency `n`. the frequency `n` of the alternating source is
View SolutionA stretched wire of length `114cm` is divided into three segments whose frequencies are in the ratio `1 : 3 : 4`, the lengths of the segments must be in the ratio :
View SolutionIf `n_(1), n_(2 ) "and" n_(3)` are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency n of the string is given by
View SolutionIf at STP, velocity of sound in a gas `(y=1.5)` is `600m//s`, the rms velocity of the gas molecules at STP will be
View SolutionIf the speed of sound is changed by 1 per cent, how much must the temperature of air neae `0^(@)C` be changed
View SolutionCalculate the ration of speed of sound in neon to that in water vapours at any temperature. Molecular weight on neon `=2.02xx10^(-2)kg//mol e` and for water vapours, molecular weight is `1.8xx10^(-2)kg//mol e`.
View SolutionThe speed of sound in oxygen `(O_2)` at a certain temperature is `460ms^-1`. The speed of sound in helium (He) at the same temperature will be (assume both gases to be ideal)
View SolutionIf the young's modulus of the material of the rod is `2 xx 10^(11) N//m^(2)` and its density is `8000 kg//m^(3)` then the time taken by a sound wave to traverse 1m of the rod will be
View Solutionv34
View SolutionVelocity of hydrogen at NTP is V. The velocity of sound in a mixture of hydrogen and oxygen in the ratio of `4:1` at NTP is
View SolutionCalculate the velocity of sound in a mixture of two gases obtained by mixing `V_(1)` and `V_(2)` volumes of them if the velocity of sound in them be `C_(1)` and `C_(2)`. The atomicity of the gases is the same.
View SolutionThe air column in a pipe which is closed at one end will be in resonance with a vibrating tuning fork at a frequency `260Hz`, if the length of the air column is (speed of sound in air `=330ms^(-1)`)
View SolutionA cylindrical tube, open at the both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of it is in water . The fundamental frequency of the air column is now-
View SolutionAn open pipe and a closed pipe are in resonance with each other with their first overtones. The ratio of their lengths are
View SolutionA pipe of length `85cm` is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below `1250 Hz`. The velocity of sound in air is `34m//s`.
View SolutionA tuning fork of frequency 340Hz vibrated above a cylindrical hallow tube closed at one end. The height of the tube is 120cm . Water is slowly poured in it. What is the minimum height of water required for resonance ?
View SolutionAn organ pipe `P_(1)`, closed at one end and containing a gas of density `rho_(1)` is vibrating in its first harmonic. Another organ pipe `P_(2)`, open at both ends and containing a gas of density `rho_(2)`, is vibrating in its third harmonic. Both the pipes are in resonance with a given tuning fork. If the compressibility of gases is equal in both pipes, the ratio of the lengths of `P_(1)` and `P_(2)` is (assume the given gases to be monoatomic)
View SolutionThe vibrations of four air columns are represented in the adjoining figures. The ratio of frequencies `n_(p) : n_(q) : n_(r) : n_(s)` is
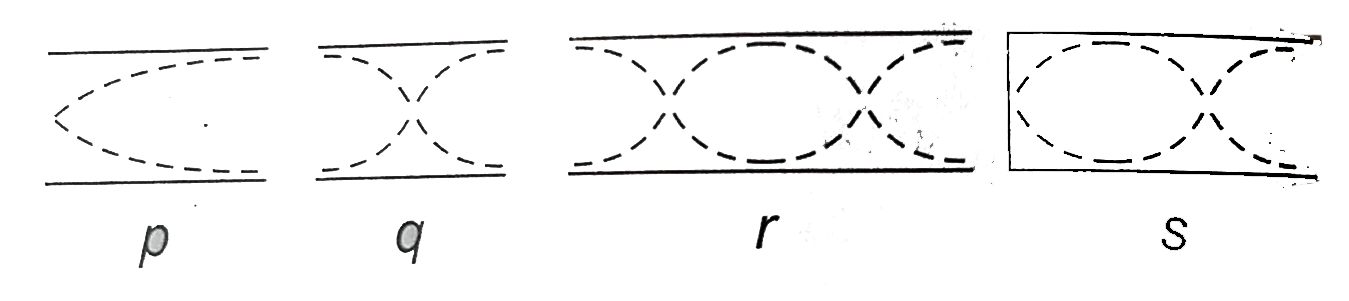
View SolutionAn open pipe of length `24cm` is in resonance with a frequency `660Hz` in fundamental mode. The radius of pipe is `(V=330ms^(-1))`
View SolutionAn open organ pipe has length `l` .The air in it vibrating in `3^( rd )` overtone with maximum amplitude `A` . The amplitude at a distance of `(l)/(16)` from any open end is.
View SolutionThe frequency of a stretched uniform wire under tension is in resonance with the fundamental frequency of a closed tube. If the tension in the wire is increased by 8 N , it is in resonance with the first overtone of the closed tube. The initial tension in the wire is
View SolutionAn open pipe resonates with frequency `100Hz` and a closed pipe resonates with frequency `50Hz`. If they are joined to form a longer tube then it will resonate with frequency of (neglect end corrections)
View SolutionIn a resonance column, first and second resonance are obtained at depths 22.7 cm and 70.2 cm. The third resonance will be obtained at a depth
View SolutionA 'pop' gun consists of a tube 25 cm long closed at one end by a cork and at the other end by a tightly fitted piston. The piston is pushed slowly in. When the pressure rises to one and half times the atmospheric pressure, the cork is violently blown out. Calculate the frequency of the 'pop' caused by its ejection. Speed ofsound in air is 340 m/s
View SolutionWhen tuning forks A and B are sounded together `5` beats per second are heard. Frequency of A is `250Hz`. On loading A with wax `2` beats per second are produced with B. The frequency of B is
View SolutionTwo open pipes of length `20cm` and `20.1cm` produces `10` beats/s. The velocity of sound in the gas is
View SolutionTwo tuning forks have frequencies `200Hz` and x. When they are sounded together `4` beats/sec are heard. The value of x is
View SolutionA tuning fork of frequency 480 Hz produces 10 beats per second when sounded with a vibrating sonometer string. What must have been the frequency of the string if a slight increase in tension produces lesser beats per second than before
View SolutionFive beats per second are produced on vibrating two closed organ pipes simultaneously. If the ratio of their lengths is `21 : 20 `, then their frequencies will be
View SolutionAn accurate and reliable audio oscillator is used to standardize a tuning fork. When the oscillator reading is `514Hz`, two beats are hear per second. When the oscillator reading is `510Hz`, the beat frequency is `6Hz`. The frequency of the tuning fork is
View Solution25 tuning forks are arranged in series in the order of decreasing frequency. Any two successive forks produce 3 beats/sec. If the frequency of the first turning fork is the octave of the last fork, then the frequency of the 21st fork is
View SolutionA tuning fork produces `4` beats/s with a sonometer wire when its lengths are `50cm` , `51cm` . The frequency of that tuning fork is
View SolutionIn a closed tube when air column is `20cm` it is in resonance with tuning fork A. When the length is increased by `2cm` then the air column is in resonance with tuning fork B. When A and B are sounded together they produce `8` beats per second . The frequencies of the tuning forks A and B are (in Hz)
View SolutionA closed organ pipe and an open organ pipe of some length produce ` 2 beats ` when they are set up into vibration simultaneously in their fundamental mode . The length of the open organ pipe is now halved and of the closed organ pipe is doubled , the number of beats produced will be
View SolutionA closed pipe is suddenly opened and changed to an open pipe of same length . The fundamental frequency of the resulting open pipe is less than that of `3rd` hoarmonic of the earlier closed pipe by `55Hz`. Then , the value of fundamental frequency of the closed pipe is
View SolutionA fork gives 5 beats with a 40cm length of sonometer wire. If the length of the wire is shortened by 1cm, the number of beats is still the same. The frequency of the fork is
View SolutionTwo tuning forks `A and B` are sounded together and `8 beats//s` are heard . `A` is in resonance with a column of air `32 cm` long in a pipe closed at one end and `B` is increased by one `cm`. Calculate the frequency of fork .
View SolutionAn organ pipe, open from both end produces 5 beats per second when vibrated with a source of frequency 200 Hz . The second harmonic of the same pipes produces 10 beats per second with a source of frequency 420 Hz . The frequency of source is
View SolutionWhen a vibrating tuning fork is placed on a sound box of a sonometer, 8 beats per second are heard when the length of the sonometer wire is kept at 101cm or 100cm. Then the frequency of the tuning frok is (consider that the tension in the wire is kept constant)
View SolutionThe two parts of a sonometer wire divided by a movable knife edge , differ in length by `2 mm` and produce `1 beat//s` , when sounded together . Find their frequencies if the whole length of wire is `1.00 m`.
View SolutionWhen an air column at `27^(@)C` and a tuning fork are sounded together, 5 beats per second are produced. The frequency of the fork is less than that of air column. No beat is heard at `-3^(@)C`. Determine the frequency of the fork.
View SolutionThe wavelength of two sound notes in air are `(40)/(195)m` and `(40)/(193)m`. Each note produces `9` beats per second, separately with a third note of fixed frequency. The velocity of sound in air in m//s is
View SolutionA train in approaching a station with a uniform velocity of `72kmph` and the frequency of the whistle of that train is `480Hz`. The apparent increase in the frequency of that whistle heard by a stationary observer on the platform is (Velocity of sound in air is `340m//s`)
View SolutionA train is travelling at `120kmph` and blows a whistle of frequency `1000Hz` . The frequency of the note heard by a stationary observer if the train is approaching him and moving away from him are (Velocity of sound in air `=330=ms^(-1)`)
View SolutionA source and an observer move away from each other with a velocity of 10 m/s with respect to ground. If the observer finds the frequency of sound coming from the source as 1950 Hz , then actual frequency of the source is (velocity of sound in air = 340 m/s )
View SolutionAn observer is moving on a circular path of radius `r` with speed `V_(0)` around source kept at centre. The apparent frequency observed by observer is (n is actual frequency)
View SolutionA source of sound moves towards a listener with a velocity equal to that of sound. If the source emits n waves per second, then the listener moving away from the source with the same velocity receives
View SolutionA source of sound and an observer are approaching each other with the same speed which is equal to `(1)/(10)` times the speed of sound. The apparent change in the frequency of the source is
View SolutionA source of sound produces waves of wave length `48cm`. This source is moving towards north with speed `1//4` th that of sound the apparent wave length of the waves to an observer standing south of the moving source will be
View SolutionA whistle producing sound waves of frequencies `9500 Hz` and above is approaching a stationary person with speed `vms^(-1)`. The velocity of sound in air is `300 ms^(-1)`. If the person can hear frequencies upto a maximum of `10,000 Hz`.The maximum value of `v` upto which he can hear whistle is
View SolutionA whistle of frequency 540 Hz rotates in a horizontal circle of radius 2 m at an angular speed of 15 rad//s. The highest frequency heard by a listener at rest with respect to the centre of circle (velocity of sound in air =`300 ms^-1`)
View SolutionIf a source emitting waves of frequency f moves towards an observer with a velocity `v//3` and the observer moves away from the source with a velocity `v//4`, the apparent frequency as heard by the observer will be (`v=` velocity of sound)
View SolutionThe velocity of a listener who is moving away from a stationary source of sound such that the listener notices `5%` apparent decrease in frequency of sound is
(Velocity of sound in air `=340m//s`)
View SolutionTwo trains are moving towards each other on parallel tracks at speeds of `144kmph` and `54kmph`. The first train sounds a whistle of frequency `600Hz`. Frequency of the whistle as heard by a passenger in the second train is (`V=340m//s`)
View SolutionA boy sitting on a swing which is moving to an angle of `30^(@)` from the vertical is blowing a whistle which is of frequency `1000Hz`. The whistle is `2m` from the point of support of the swing. If a girl stands in front of the swing, the maximum and minimum frequencies she will hear are
(velocity of sound `=330m//s`, `g=9.8m//s^(2)`)
View SolutionA source of sound produces waves of wave length `48cm`. This source is moving towards north with speed `V//4` where V is speed of sound. The apparent wavelength of the waves to an observer standing south of the moving source will be
View SolutionA siren of frequency n approaches a stationary observer and then receedes from the observer. If the velocity of source `(V) lt lt ` the velocity of sound `(C )`, the apparent change in frequency is
View SolutionTwo sources `S_(1) and S_(2)` of sound having frequencies 338, 342 Hz are separated by a large distance. The speed of sound is 340 m/s. The velocity of the observer who is moving from `S_(2) " to " S_(1)` so that he does not hear any beats is
View SolutionA vehicle moving on a straight road sounds a whistle of frequency `256Hz` while nearing a hill with a velocity `10ms^(-1)`. The number of beats per second observed by a person travelling in the vehicle is `(V=330ms^(-1))`
View SolutionIf a vibrating tuning fork of frequency `255Hz` is approaching with a velocity `4m//s` perpendicular to a wall. The number of beats produced per sec is (speed of sound in air `=340m//s`)
View SolutionTwo sources A and B are sounding notes of frequency 680 Hz. A listener moves from A to B with a constant velocity u. If the speed of sound is 340 m/s, What must be the value of u so that he hears 10 beats per second?
View Solution
Exercise-I (H.W) questions and complete solutions for chapter WAVES of NARAYANA PHYSICS (HINGLISH) of Class 11