Complete Solutions to All Questions of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NCERT EXEMPLAR | All Questions |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
The displacement of a particle is represented by the equation `y=3cos((pi)/(4)-2omegat).`
The motion of the particle is
View SolutionThe displacement of a particle is repersented by the equation `y=sin^(3)omegat`. The motion is
View SolutionThe relation between acceleration and displacement of four partical are given below
Which, one of the particle is exempting simple harmonic motion ?
View SolutionMotion of an oscillating liquid column in a U-tube is
View SolutionA particle is acted simultaneously by mutally perpendicular simple harmonic motion `x=acosomegat` and `y=asinomegat`. The trajectory of motion of the particle will be
View SolutionThe displacement of a particle varies with time according to the relation `y=asinomegat+bcoasomegat`.
View SolutionFour pendulums A, B, C and D are suspended from the same

elastic support as shown in figure. A and C are of the same length, while B is smaller than A and D is larger than A. If A is given a transverse displacement,
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
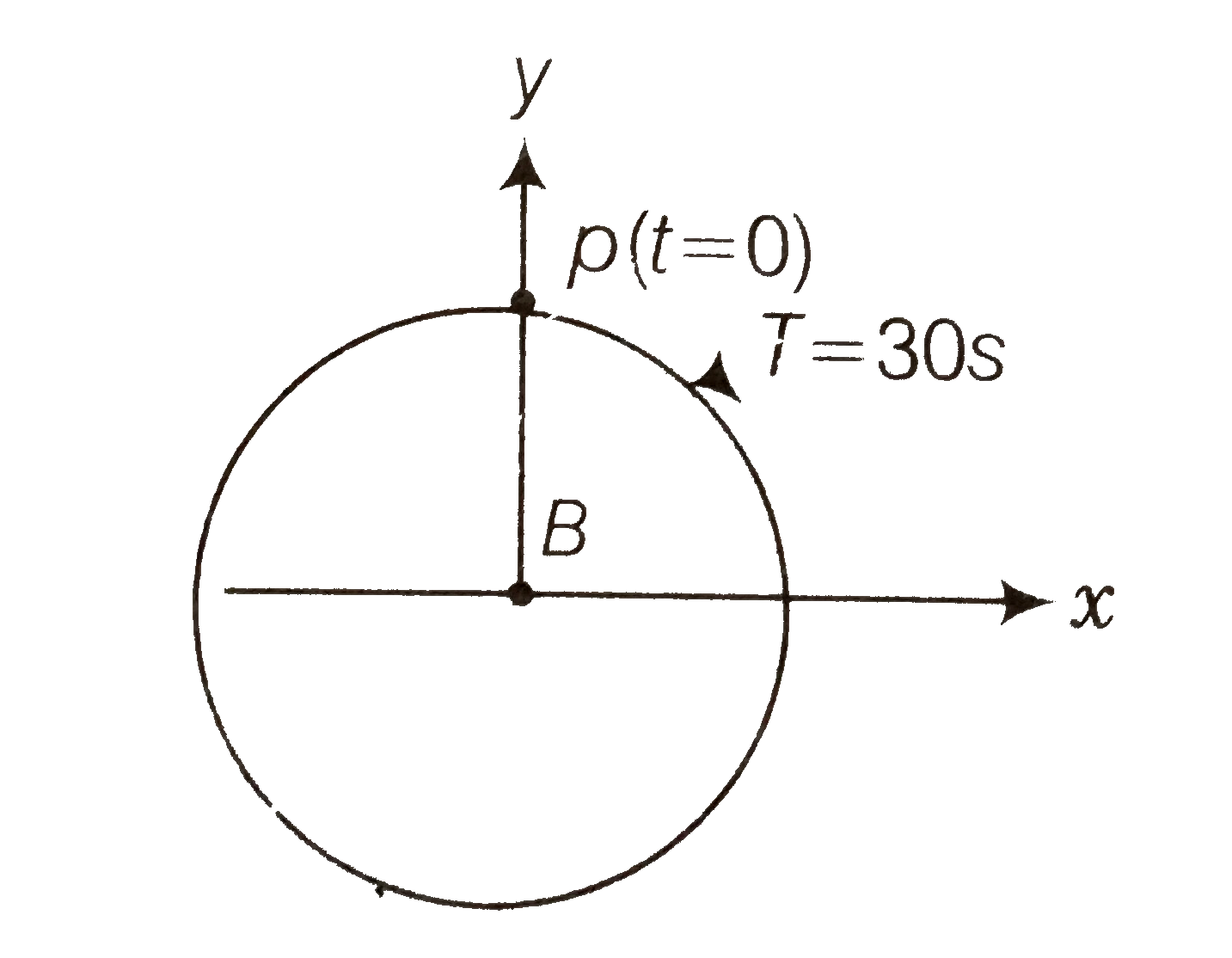
View SolutionThe equation of motion of a particle is `x=acos(alphat)^(2)`. The motion is
View SolutionA particle executing SHM has a maximum speed of `30 cm//s` and a maximum acceleration of `60 cm/s^(2)` . The period of oscillation is
View SolutionWhen a mass m is connected individually to two springs `S_(1)` and `S_(2)`, the oscillation frequencies are `v_(1)` and `v_(2)`. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be

View SolutionThe rotation of earth about its axis is
a) Periodic motion
b) Simple harmonic motion
c) Periodic but not simple harmonic motion
d) Non- Periodic motion
View SolutionMotion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is
View SolutionDisplacement versus time curve for a particle executing SHM is shown in figure. Choose the correct statements.

View SolutionWhich of the following statements is/are true for a simple harmonic oscillator ?
View SolutionThe displacement-time graph of a particle executing SHM is shown in figure. Which of the following statement is/are true ?
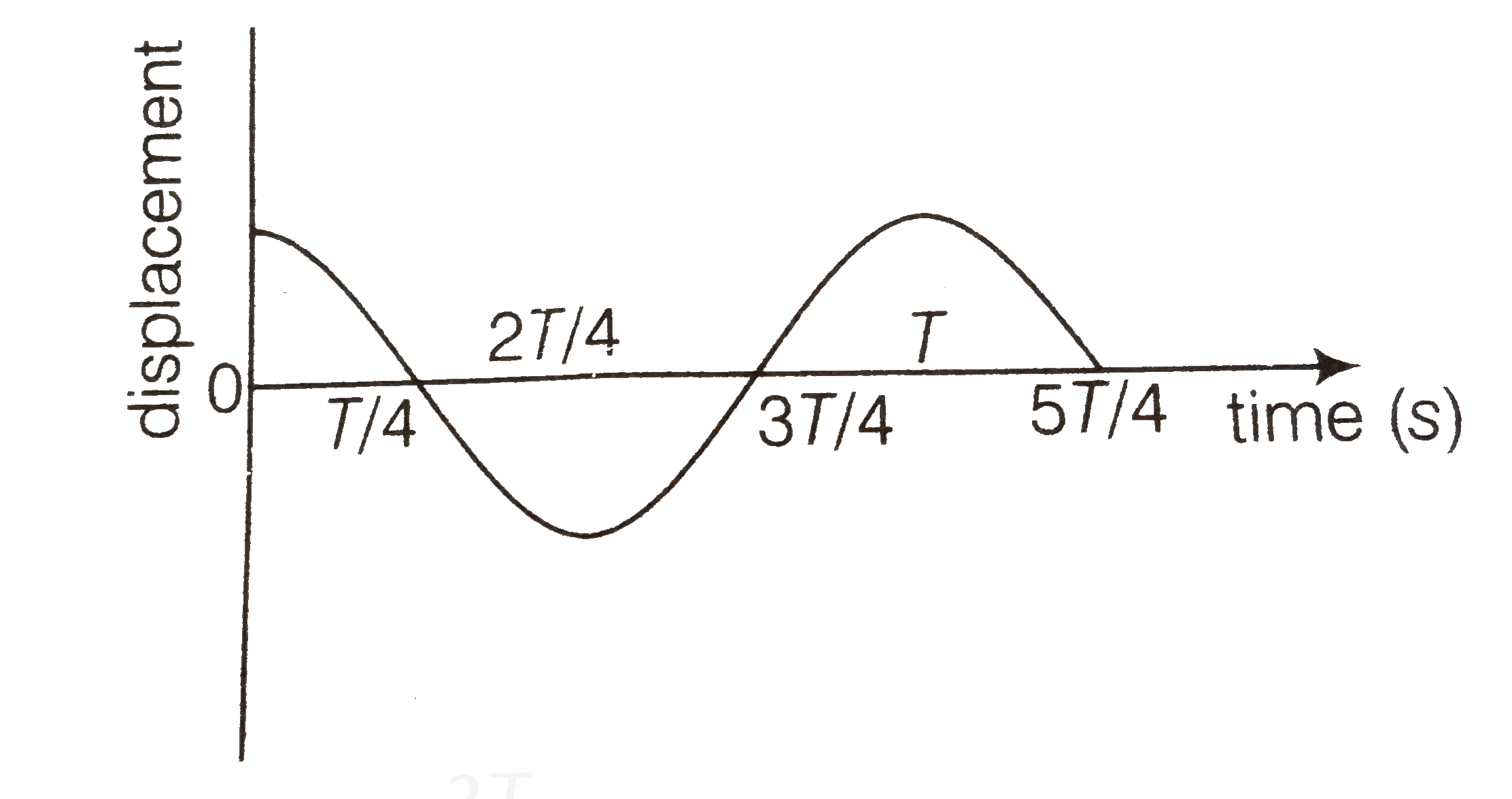
View SolutionA body is performing SHM, then its
View SolutionDisplacement versus time curve for a particle executing SHM is shown in figure. Identify the points marked at which
(i) velocity of the oscillator is zero,
(ii) speed of the oscillator is maximum.
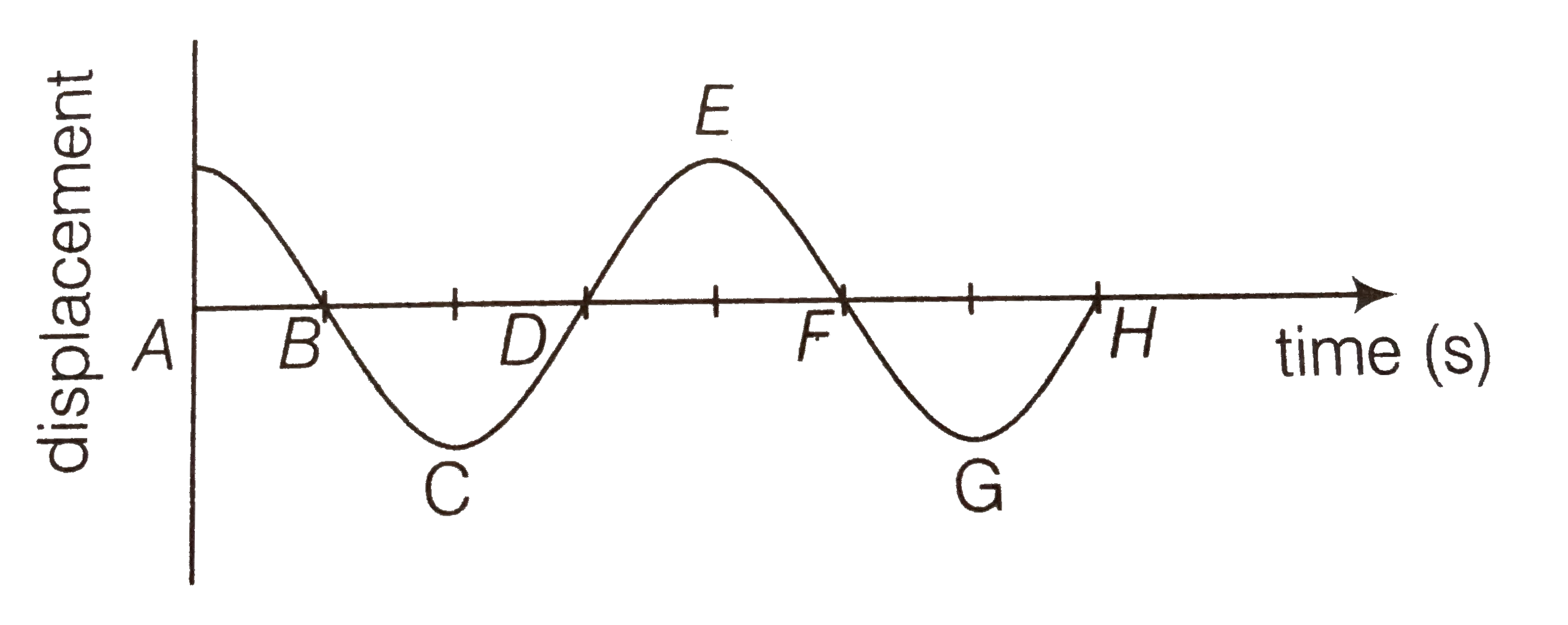
View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionWhat are the two basic characteristics of a simple harmonic motion?
View SolutionWhen will the motion of a simple pendulum be simple harmonic?
View SolutionWhat is the ratio of maximum acceleration to the maximum velocity of a simple harmonic oscillator?
View SolutionWhat is the ratio between the distance travelled by the oscillator in one time period and amplitude?
View SolutionIn figure, what be the sign of the velocity of the point P', which is the projection of the velocity of the reference particle P.P is moving in a circle of radius R in anti-clockwise direction.

View SolutionShow that for a particle executing SHM, velocity and dispacement have a phase difference of `pi//2`.
View SolutionDraw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
View SolutionThe length of a second's pendulum on the surface of earth is 1 m. What will be the length of a second's pendulum on the moon?
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionShow that the motion of a particle represented by `y=sinomegat-cosomegat` is simple harmonic with a period of `2pi//omega`.
View SolutionFind the displacement of a simple harmonic oscillator at which its PE is half of the maximum energy of the oscillator.
View SolutionA body of mass m is situated in potential field `U(x)=U_(o)(1-cospropx)` where, `U_(o)` and `prop` are constants. Find the time period of small oscillations.
View SolutionA mass of 2kg is attached to the spring of spring constant `50Nm^(-1)`. The block is pulled to a distance of 5 cm from its equilibrium position at `x=0` on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionConsider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of `2^(@)` to the right with the vertical, the other pendulum makes an angle of `1^(@)` to the left of the vertical. What is the left of the vertical. What is the phase difference between the pendulums?
View SolutionA person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of `2.0s^(-1)` and an amplitude 5.0 cm. A weighing machine on the platform gives the persons wieght against time.
(a) Will there be any change in weight of the body, during the oscillation?
(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
View SolutionA body of mass m is attached ot one end of a massless spring which is suspended vertically form a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation?
(b) Find the frequency of oscillation?
View SolutionA cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that lon would execute SHM with a time period. `T=2pisqrt((m)/(Apg))` where, m is mass of the body and p is density of the liquid.
View Solution
All Questions questions and complete solutions for chapter OSCILLATIONS of NCERT PHYSICS (ENGLISH) of Class 11