Complete Solutions to Multiple Choice Questions of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| NCERT EXEMPLAR | Multiple Choice Questions |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
The angle between `A=hat(i)+hat(j) " and " B=hat(i)-hat(j)` is
View SolutionWhich one of the following statements is true?
View SolutionFigure shows the orientation of two vectors ` vec u` and `vec v` in the (XY) plane.
If ` vec u = a hat i + b hat j` and ` vec v = p hat i+ q hat j` which of the following is correct ?
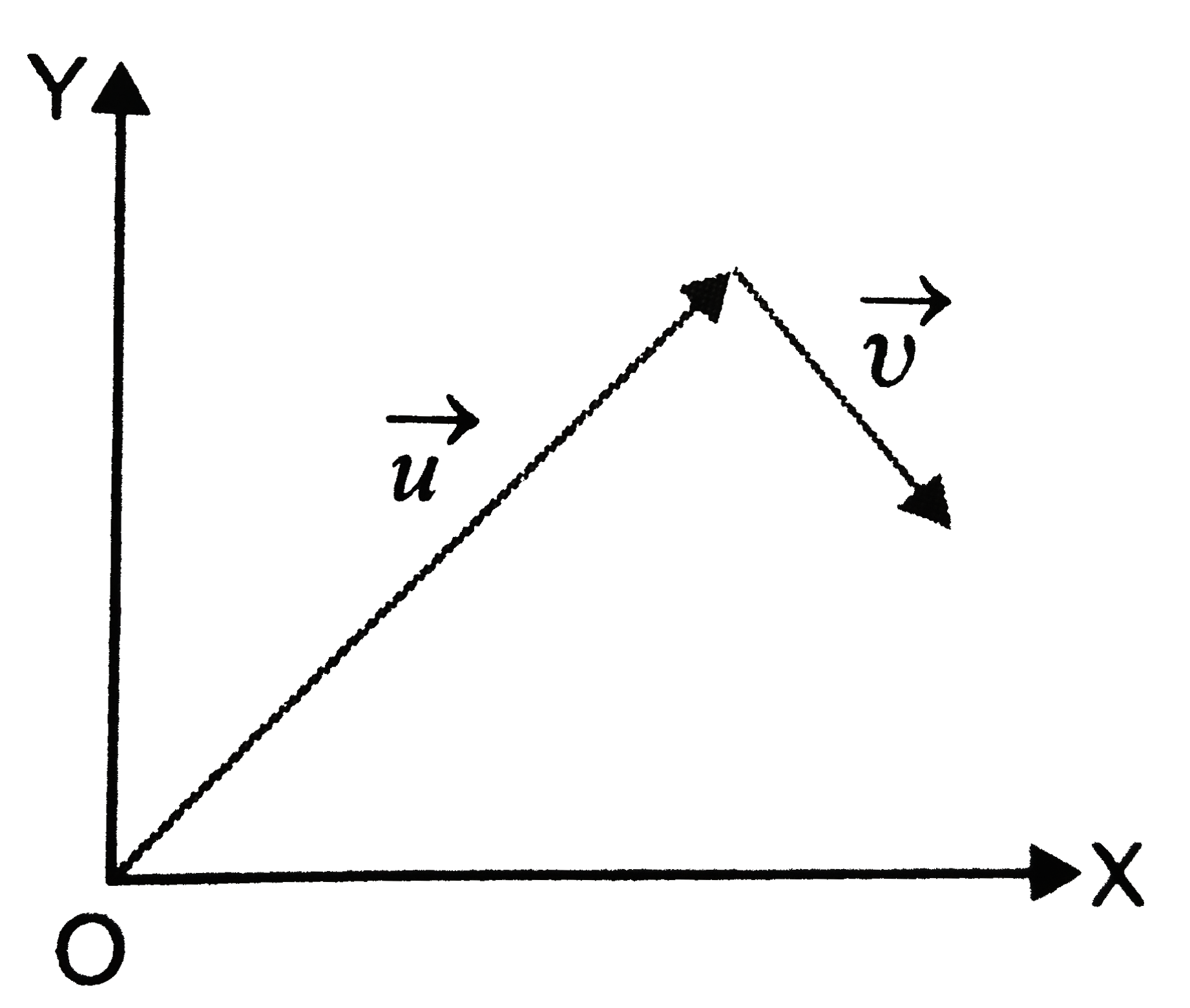 .
.
View SolutionThe component of a vector `r` along X-axis will have maximum value if
View SolutionThe range of a projectile fired at an angle of `15^@` is 50 m. If it is fired with the same speed at an angle of `45^@` its range will be
View SolutionConsider the quantities , pressure, power, energy impulse, gravitational potential, electrical charge , temperature, area,Out of these, the only vector quantities are .
View SolutionIn a two dimensional motion,instantaneous speed `v_(0)` is a positive constant.Then which of the following are necessarily true?
View SolutionIn a two dimensional motion, instantaneous speed `v_(0)` is a positive constant. Then which of the following are neccessarily true?
View SolutionThree vectors `vecA,vecB` and `vecC` add up to zero.Find which is false.
View SolutionIt is found that `|A+B|=|A|`,This necessarily implies.
View SolutionTwo particles are projected in air with speed `v_(0)` at angles `theta_(1)` and `theta_(2)` (both acute) to the horizontal,respectively.If the height reached by the first particle greater than that of the second,then thick the right choices
View SolutionA particle slides down a frictionless paraboli `(y=x^(2))` track `(A-B-C)` starting from rest at point `A`.Point `B` is at the vertex of parabola and point `C` is at a height less than that of point `A`.After `C`,the particle moves freely in air as a projectile. If the particle reaches highest point at `P`,then
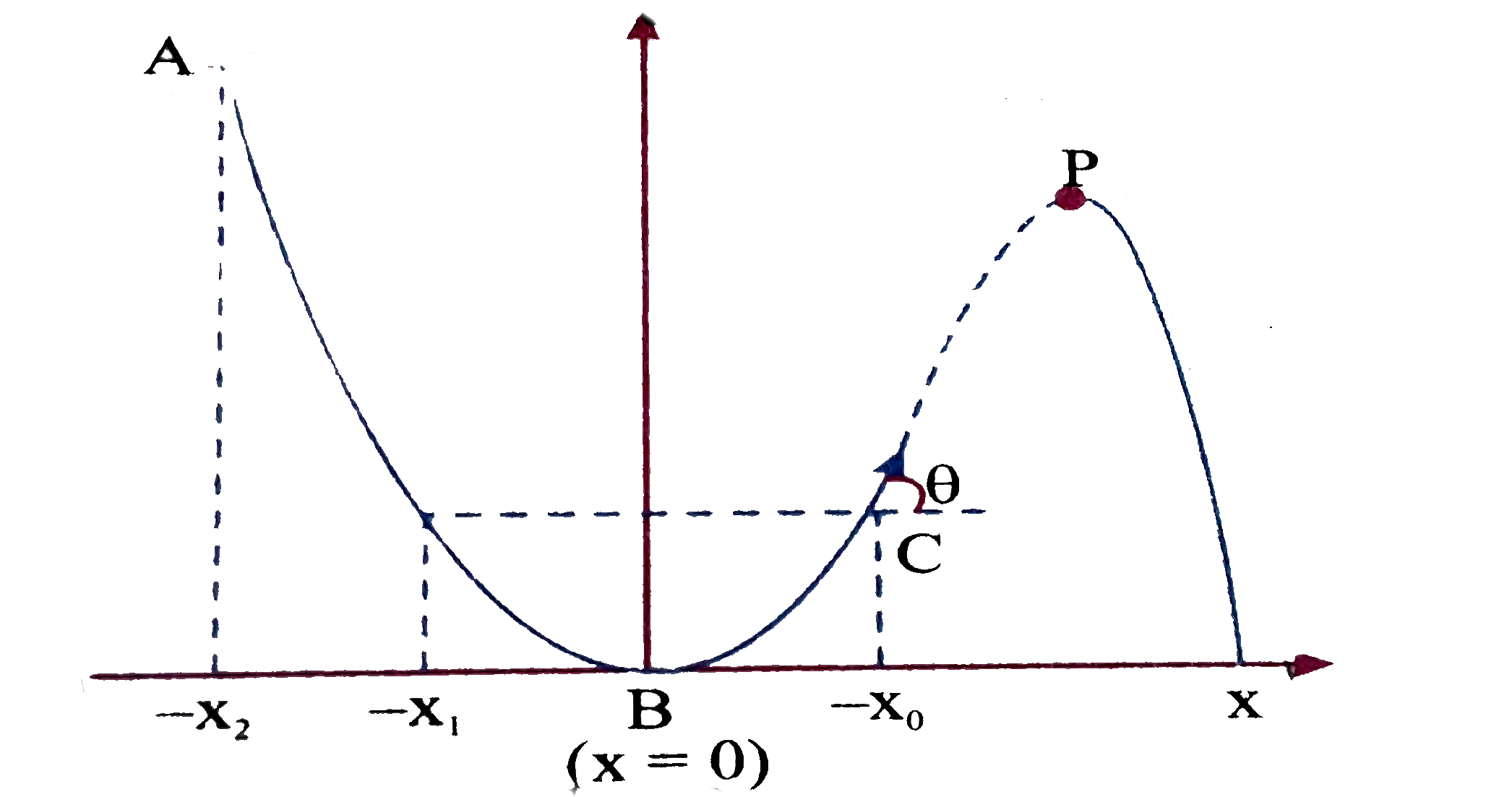
View SolutionFollowing are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s)
View SolutionFor a particle performing uniform circular motion, choose the incorrect statement from the following.
View SolutionFor tow vectros ` vec A` and `vec B`
` | vec A + vec B| = | vec A- vec B|` is always true when.
View SolutionA cyclist starts form centre ` O` of a circular park of radius ` 1 km` and moves along the path ` OPRQO`. If he maintains constant speed of ` 10 ms^(-1)`. What is his acceleration at point (R )in magnitude and direction ?
 .
.
View SolutionA particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively . Shown in the diagram, direction of velocity and acceleration at points A, B and C.
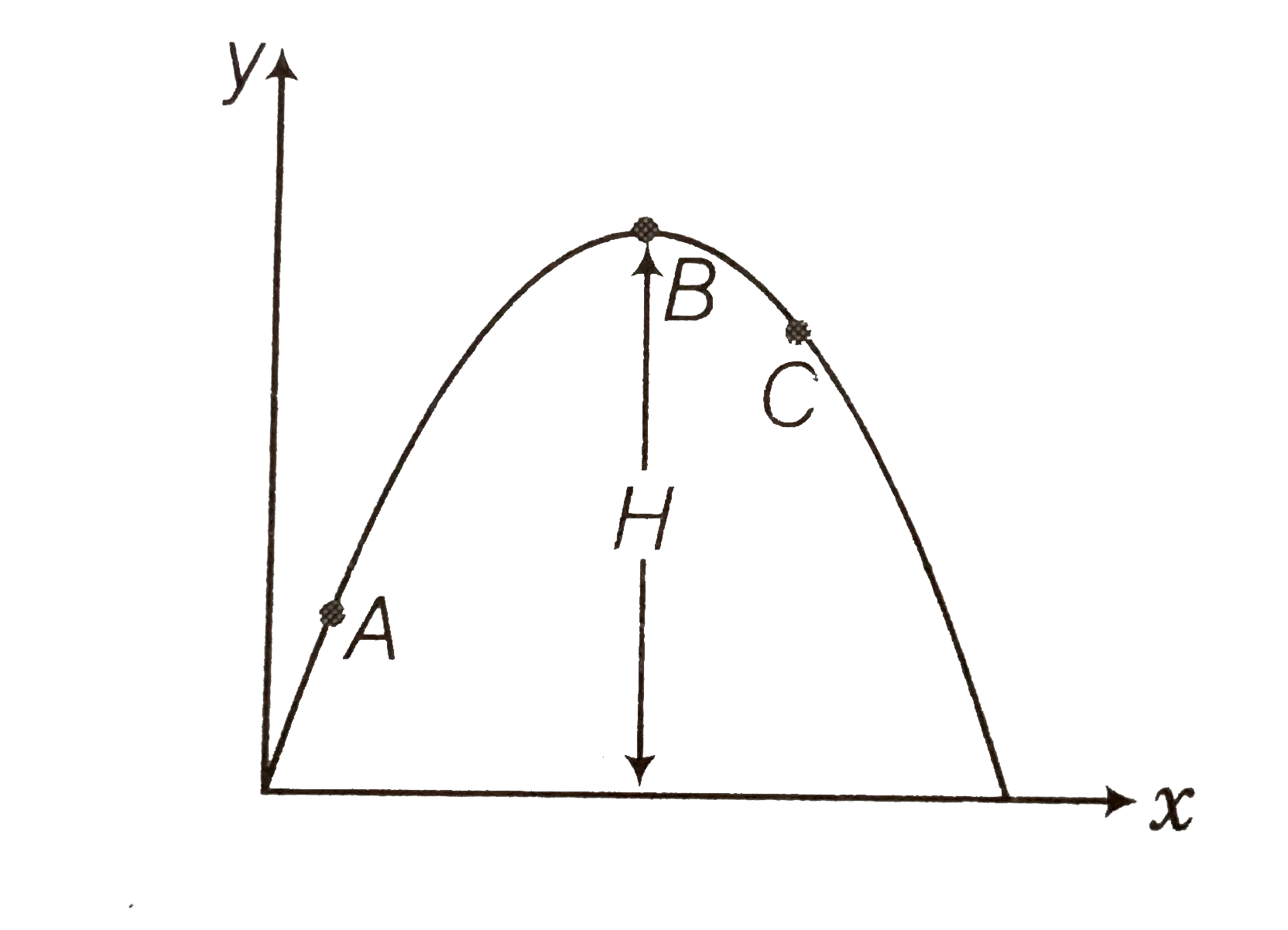
View SolutionA ball is thrown from a roof top at angle of ` 40^(@)`above the horizontal. It hits the ground a few seconds later. At what point during its motion. Does the ball have
(a) greatest speed (b) smallest speed (c ) greatest acceleration ? Explain.
View SolutionA football is kicked into the air vertically upwards. What is its (a) acceleration, and (b) velocity at the highest point ?
View Solution` vec A , vec B and vec C` are three non-collinear, non co-planar vectors. What can you say about direction of ` vec A xx vec (B xx vec C`) ?
View SolutionA boy travelling in an open car moving on a levelled road with constant speed tosses a ball vetically up in the air and catches it back. Shetch the motion of the ball as observed by a boy stanceing on the footpath. Give explanation to support your diagram.
View SolutionA boy throws a ball in air at ` 60^@` to the horizontal along a road with a speed of ` 10 m//s`. Another boy sitting in a car passing by observes the ball. Sketch the motion of the ball as observed by the boy in the car, If car has a speed of `(18 km //h)`. Give explanation to support your diagram.
View SolutionIn dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like it air resistance is included . Sketch such a trajectory and explain why you have drawn it that way.
View SolutionA fighter plane is flying horizontally at an altitude of 1.5 km with speed `720 kmh^(-1)`. At what angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target? `(Take g=10ms^(-2))`
View Solution(a) Earth can be thought of as a sphere of radius ` 64 00 km`. Any object (or a person ) is performing circula motion around the axis os earth due to earths rotation (period 1 day ). What is acceleration o object on the surface of th earth 9at equator ) towards its centre ? What is its altitude ` theta` ? How does these accelerations compare with `g=9.8 m//s^2 `?
(b) Earth also moves in circular orbit around sum every year withon orbital radius of ` 1.5 xx 10 ^(11) m`. What is the acceleration of earth ( or any object on the surface of the earth ) towards the centre of the sum ? How dies thsi acceleration comparte with ` g=9.8 ms^2 `?
View SolutionGiven below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
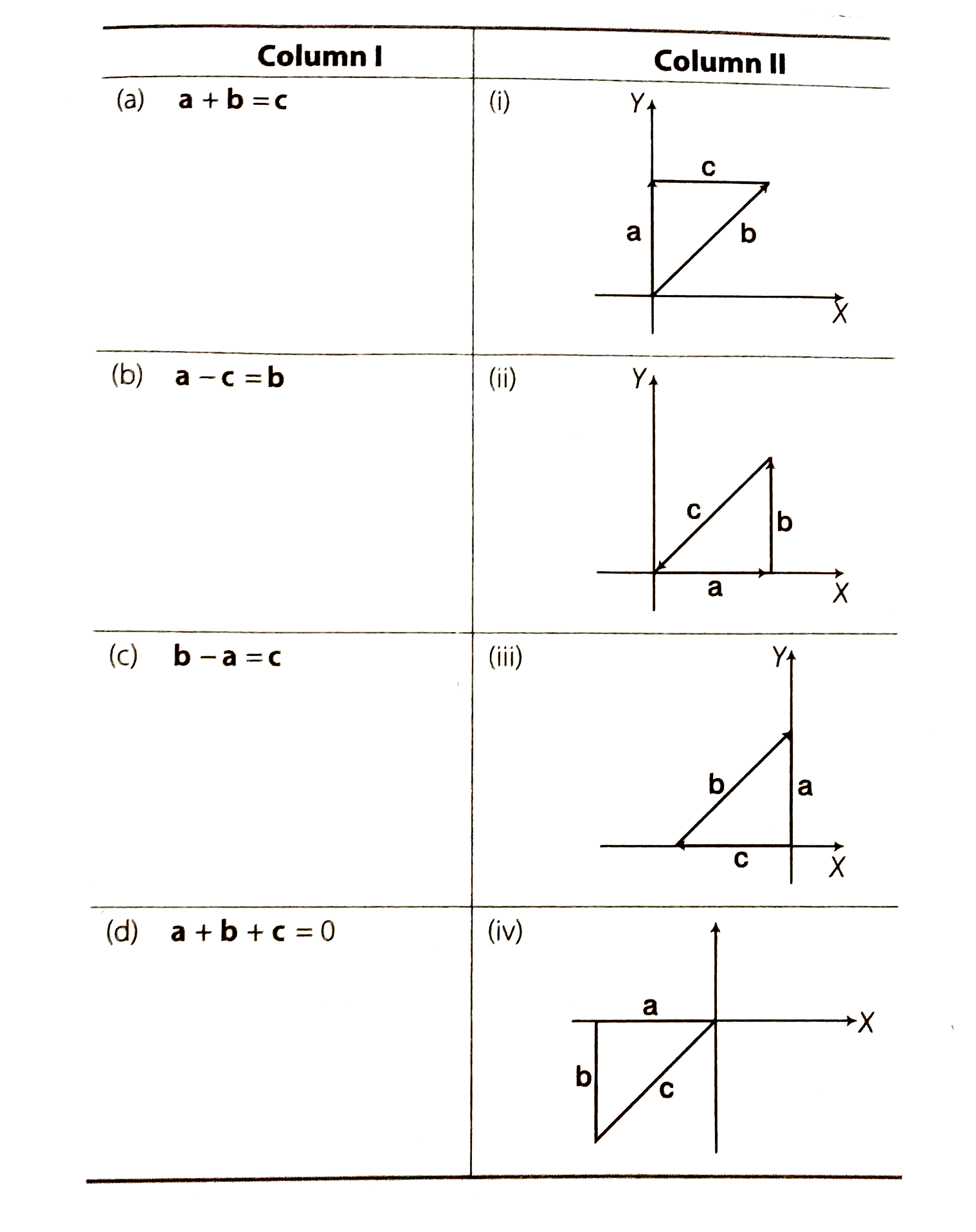
View SolutionIf |A|=2 and |B| = 4, then match the relation in Column I with the angle `theta` between A and B in Column II.
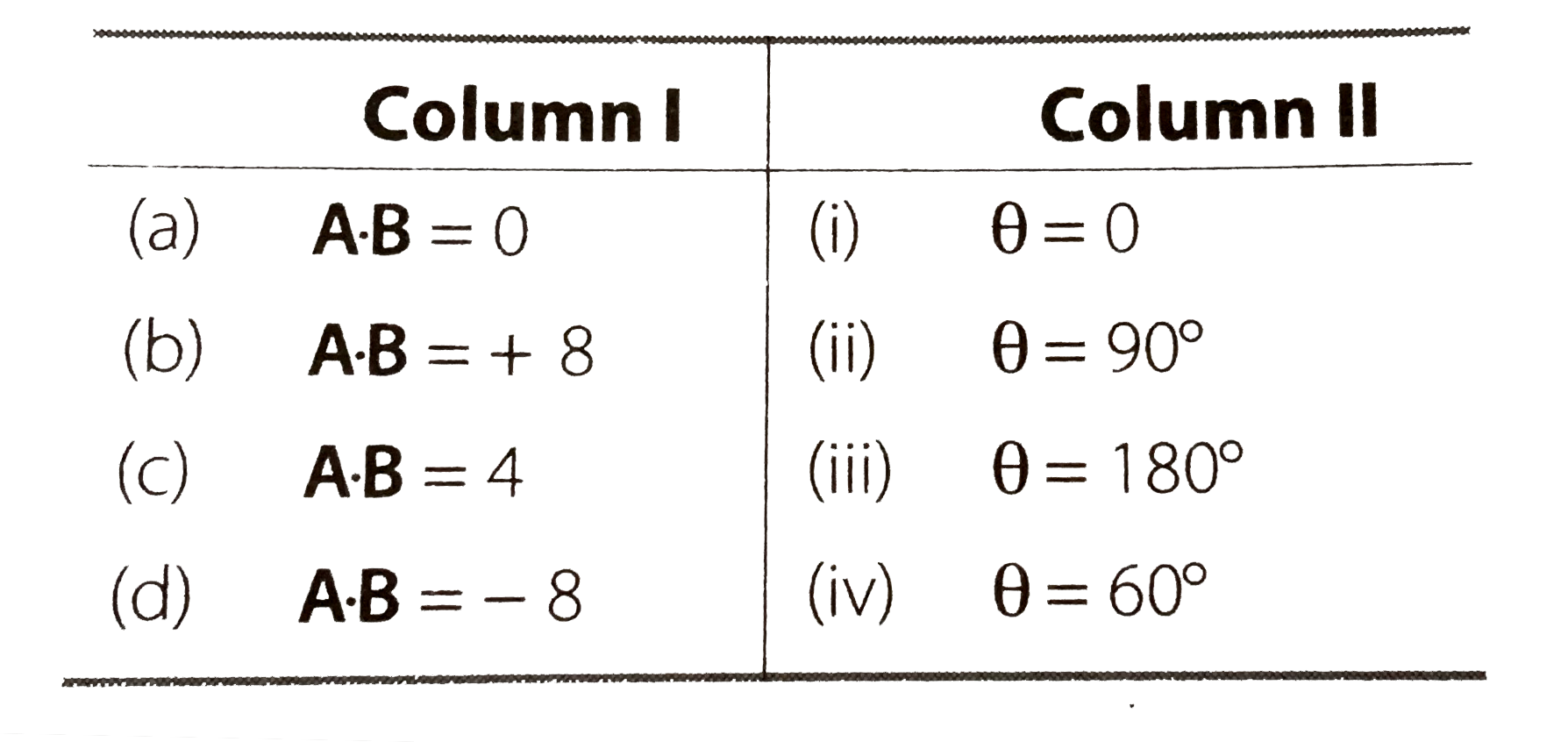
View SolutionIf ` | vec A | =2 and | vec B| =4`, then match the relations in column I with the angle` theta` between ` vec A and vec B` in column II.
Column I, Column II
(a) ` |vec A xx vec B| =0` , (i) ` theta =30^@`
(b) `| vec A xx vec B|=0` , (ii) ` theta =45^@`
(c ) ` vec A xx vec B| =4` , (iii) ` theta =90^@`
(d) ` | vec A xxx vec B| = 4 sqrt 2` , (iv) ` theta =0^@`.
View SolutionA hill is ` 500 m` high. Supplies are to be across the hill using a canon that can hurl packets at a speed of `125 m//s` over the hill . The canon is located at a distance of ` 800 m` from the foot to hill and can be veoved on the ground at a speed of 2 m//s , so that its distance from the hill can be adjusted. What is the shortest time inwhich a pachet can reach on the ground across the hill ? Taje ` g= 10 m//s^2`.
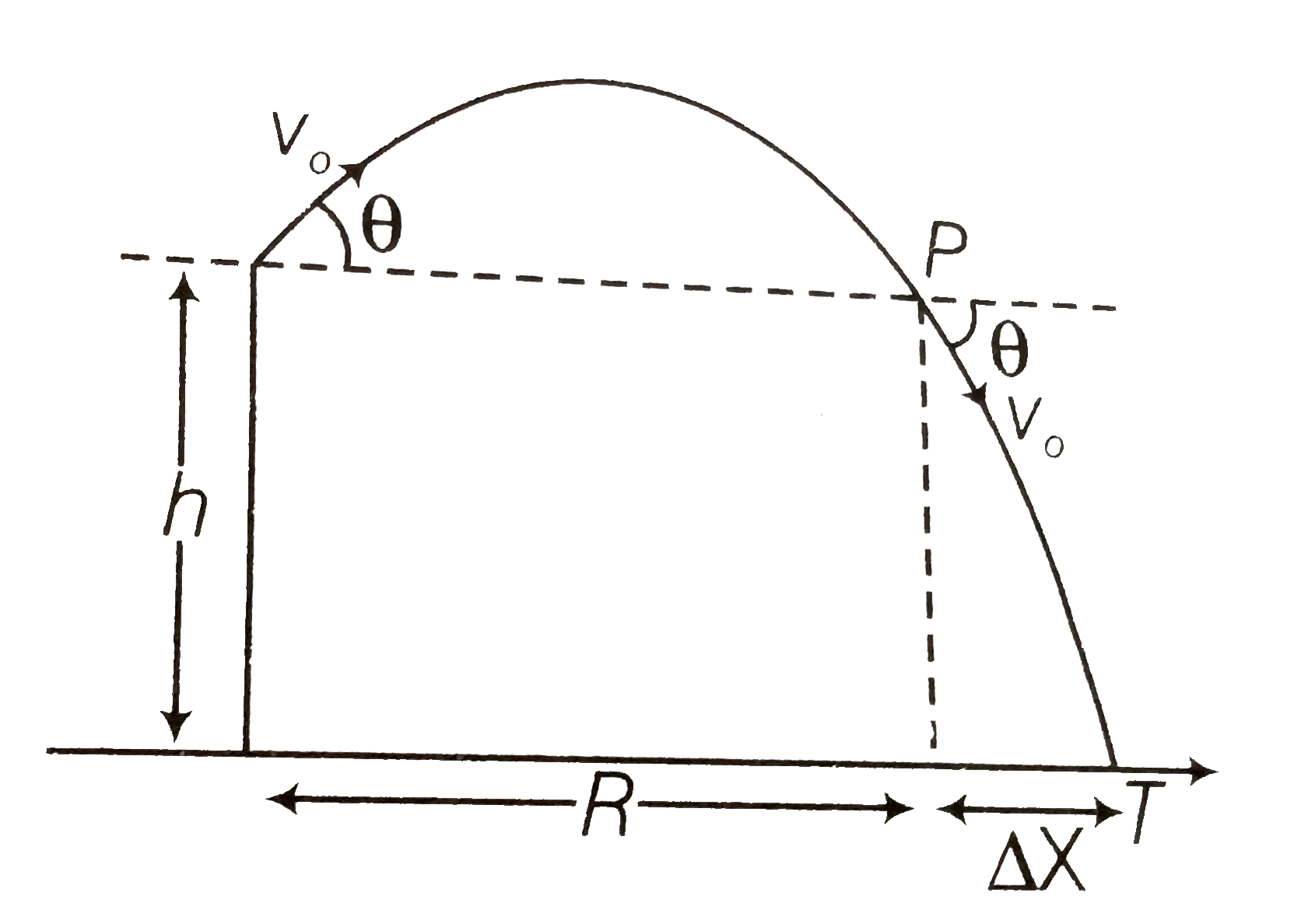
View SolutionA gun can fire shells with maximum speed `v_(0)` and the maximum horizontal range that can be achieved is `R=(v_(0)^(2))/(g)`. If a target farther away by distance `Deltax` (beyond R) has to be hit with the same gun, show that it could that it could be achieved by raising the gun to a height at least `h=Delta x[1+(Deltax)/(R)]`
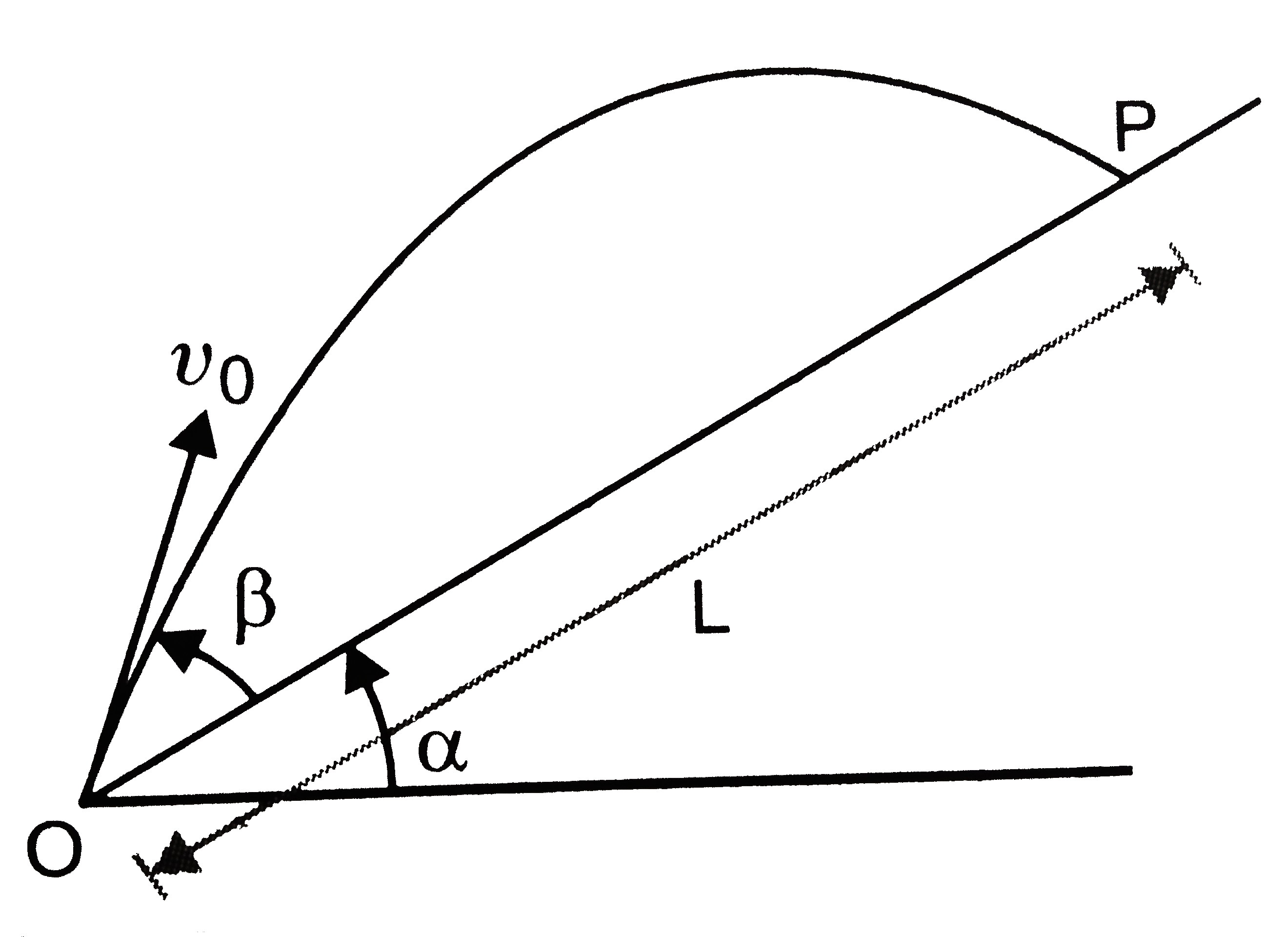
View SolutionA particle is projected in aer an angle ` beta` to a surface which itself is inclined at an angle ` alpha` to the horixonta (Fig. 2 (EP). 26)
(a) Find an ecxpression for range on the plane surface (distanc eon the plance from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) ` beta` at which range will be maximum.
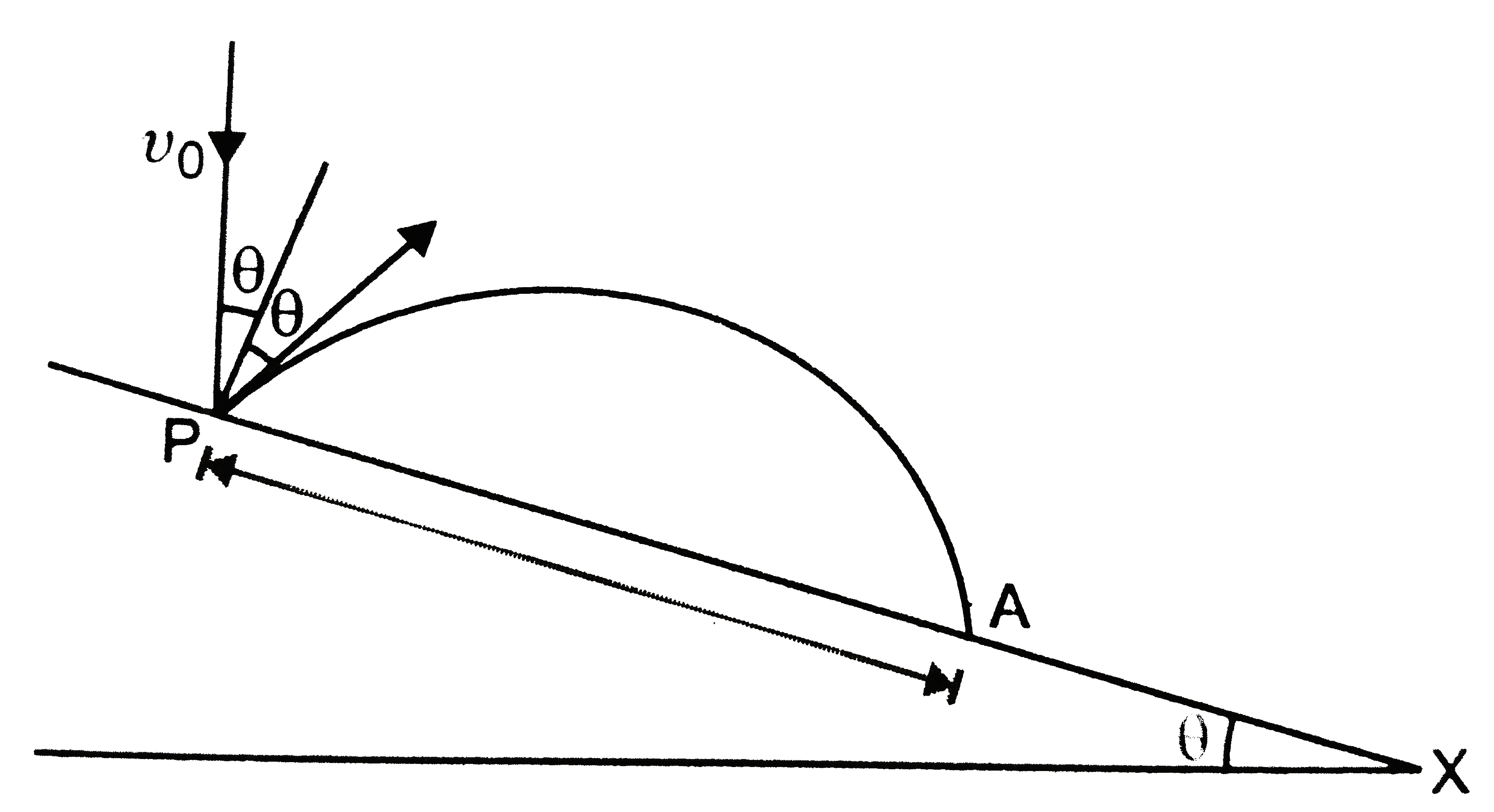
View SolutionA particle falling vertically from a height hits a plane surface inclined to horizontal at an ange ` theta` with speed ` v_0` and rebounds elastically (Fig. 2 (RP). 28). Find the distance aling the plane where it will hit second time.
 .
.
View SolutionA girl riding a bicycle with a speed of ` 5 m//s` to wards Noth direction, observes rain falling vertically down. If she increases her speed to `10 m//s`, rain appeard to meet her at ` 45^@` to the vertical . What is the speed ot the rain ? In what direction does rain fall as observed by a ground based observer ?
View SolutionA river is flowing due east with a speed ` 3 m//s` (Fig. 2 (EP) .31 ).
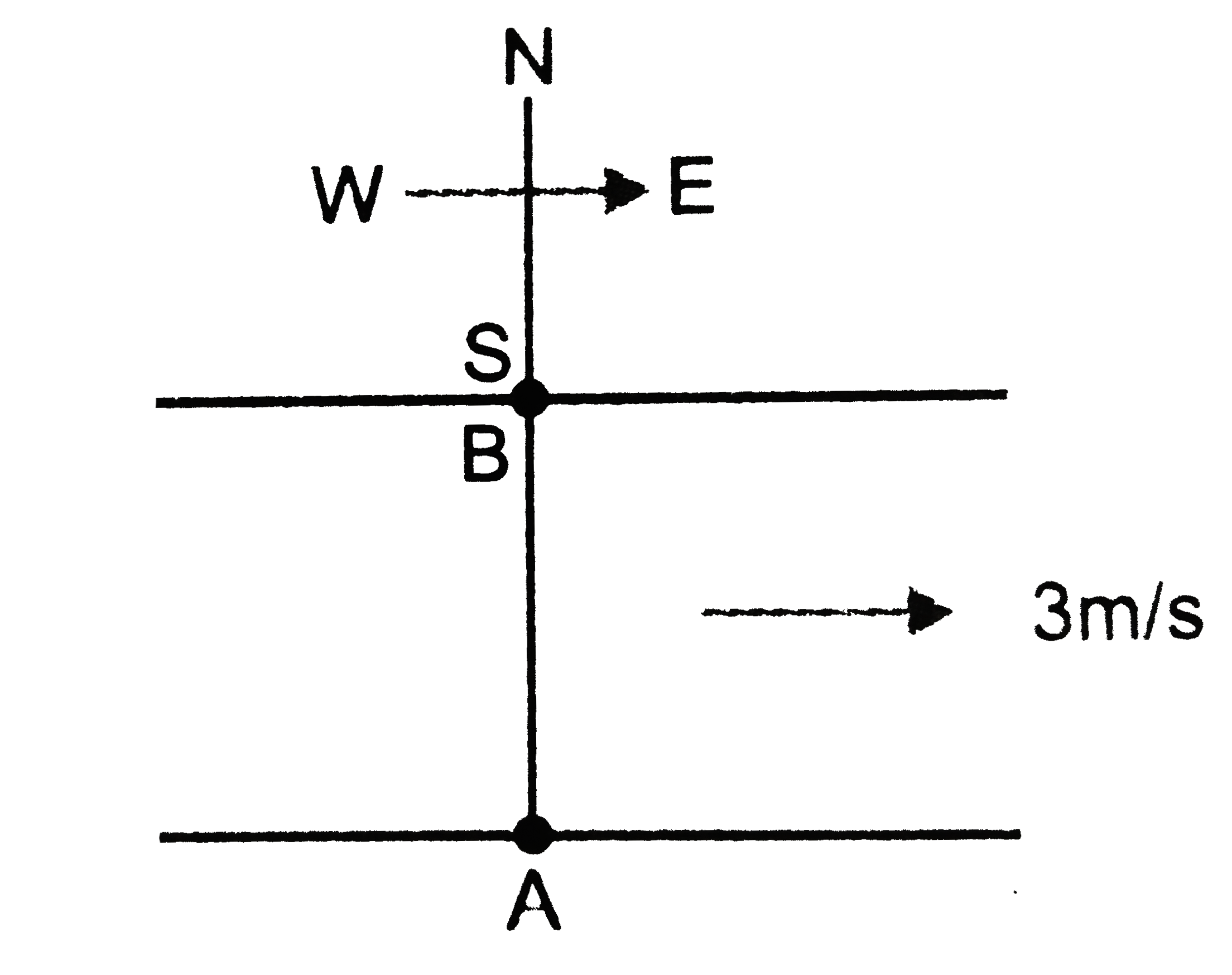 . (a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
. (a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction) ? (b) If he wants to start from point (A) on South bank and reach opposite point (B) on North bank,
(i) Which direction should he swim? (ii) What will be his resultant speed ? (c ) From two differenrent casses as mentioned in (a) and 9b) above, in which casse will he reach opposite bank in shorter time ?
View SolutionA cricket fielder can throw the cricket ball with a speed ` v_0`. If he throws the ball while running with speed (u) at angle ` theta` to the horizontal, find
(b) what will be time of flight ?
(c ) what is the distance (horizontal range) form the point of projection at which the ball will land ?
(d) find ` theta` at which he should throw the ball that would maxmise the horizontal range range as found in (c ).
(e) how does ` theta` for maximum range change if ` u gt v_0, u=v_0, ult v_0` ?
(f) how does ` theta` in (e) compare with that for ` u=0 (i.e., 45^@) ?
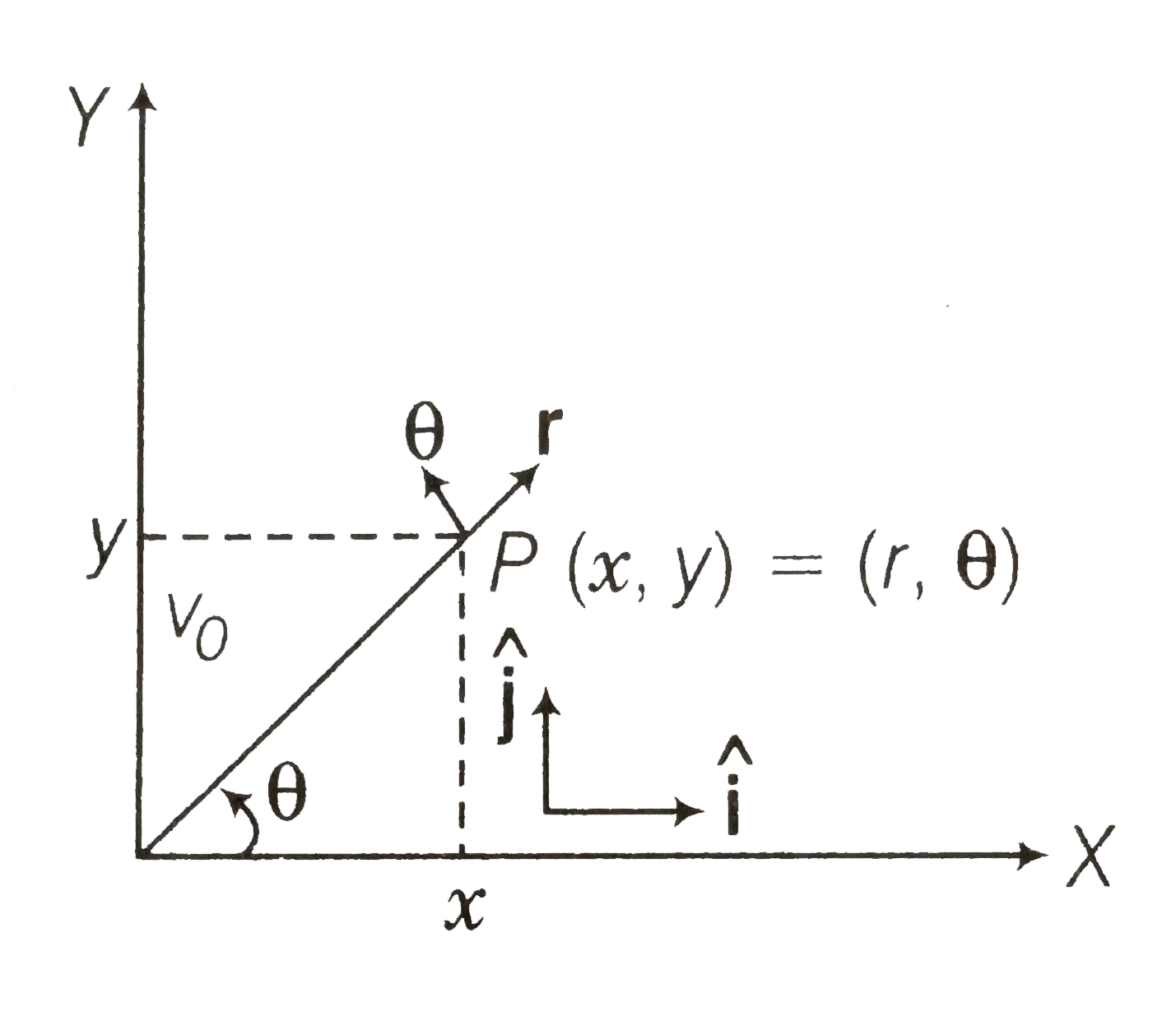
View SolutionMotion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates `A=A_(x)hat(i) + A_(y)hat(j)`, where `hat(i)` and `hat(j)` are unit vector along x and y-directions, respectively and `A_(x)` and `A_(y)` are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as `A= A_(r)hat(r) + A_(theta) hat(theta)`, where `hat(r)=(r)/(r)=cos theta hat(i)+sin theta hat (j)` and `hat(theta)=-sin theta hat(i) + cos theta hat (j)` are unit vectors along direction in which r and `theta` are increasing.
(a) Express `hat(i)` and `hat (j) ` in terms of `hat(r) ` and `hat (theta)`.
(b) Show that both `hat(r)` and `hat(theta)` are unit vectors and are perpendicular to each other.
(c) Show that `(d)/(dt)(hat(r))= omega hat(theta)`, where `omega=(d theta)/(dt)` and `(d)/(dt) (hat(theta))=-thetahat(r)`.
(d) For a particle moving along a spiral given by `r=a theta hat(r)`, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
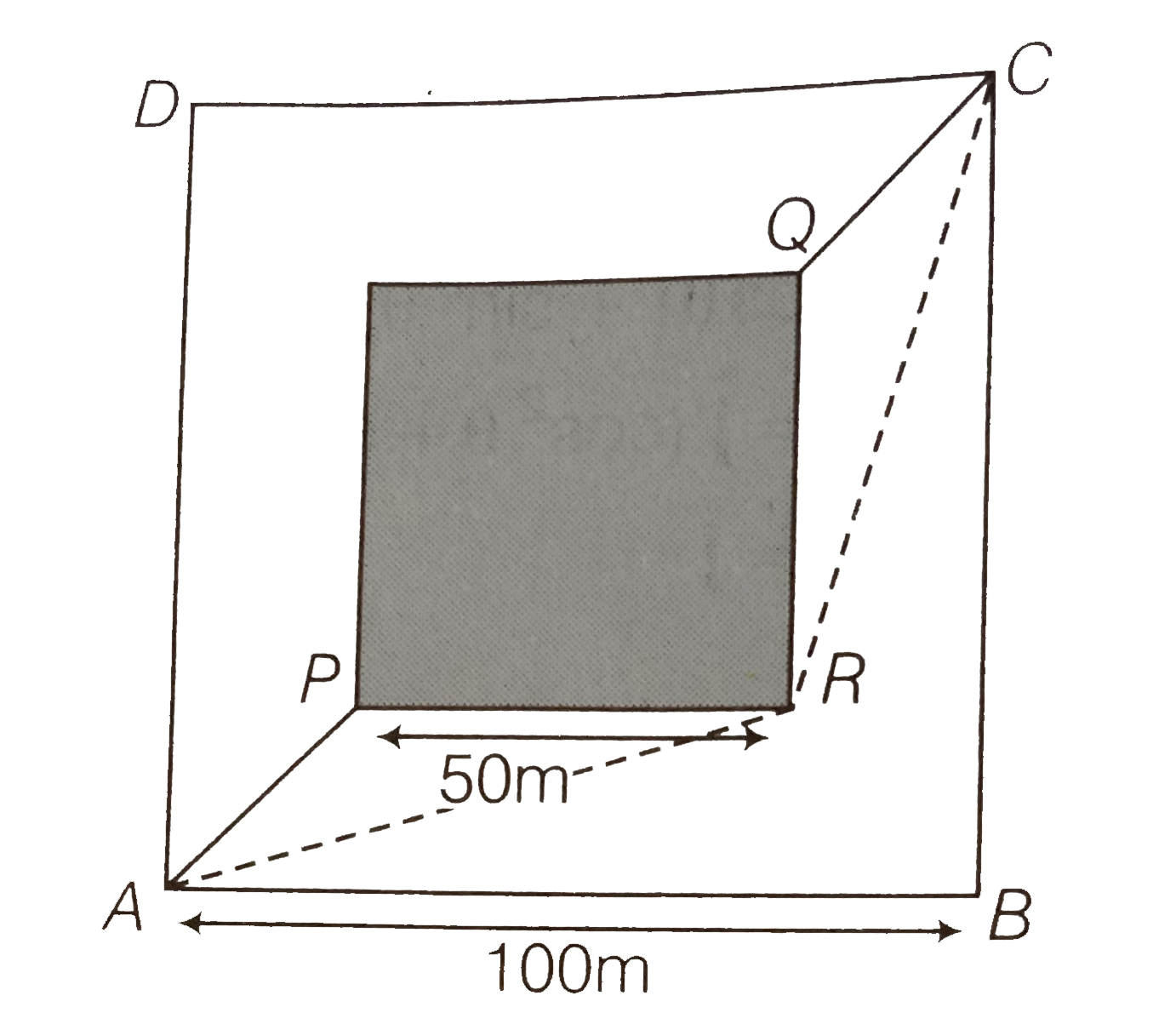
View SolutionA man wants to reach from A to the opposite corner of the square C. The sides of the square are 100 m. A central square of `50mxx50m` is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square , he can walk only at a speed of v m/s `(v lt 1)`. What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand ?
View Solution
Multiple Choice Questions questions and complete solutions for chapter MOTION IN A PLANE of NCERT PHYSICS (HINGLISH) of Class 11