Complete Solutions to Illustrative Example of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PHYSICS GALAXY | Illustrative Example |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
Road distance from Jaipur to Ajmer is 135km. How long can one afford to stop for lunch if he can drive at an average speed of 72 kmph on the highway, if he has to reach in `2^(1//2) hr`
View SolutionA 10 hr tour is made at an average speed of 40 kph. Ifduring the first half of the distance the average speed of the bus was 30 kph, what was the average speed for the second half of the trip?
View SolutionA carrier train, when it is 100 km away from the station, going at a constant speedof 70 kph towards the station. At this instant a fast bird from its engine flies towards the station at 100 kph net speed.When the bird gets to the station, it turns back and flies again towards the train, when it reaches engine, it again turns and heads towards the station. If bird keep son flying in such a manner, find the distance travelled by the bird before train reaches the station ? How many trips, it made in this duration between station and the train ?
View SolutionAn athlete starts running along a circular track of 50 m radius at a speed `5 m//s` in the clockwise direction for 40 s. Then the athlete reverses direction and runs inthe anticlockwise direction at 3 m/s for 100 s. At the end, how far around the track is the runner from the starting point ?
View SolutionA motorboat going downstream overcome a raft at a point A, `tau=60min` later it turned back and after some time passed the raft at a distance `l=6.0km` from the point A. Find the flow velocity assuming the duty of the engine to be constant.
View SolutionTwo ships, 1 and 2, move with constant velocities 3 m/s and 4 m/s along two mutually perpendicular straight tracks toward the intersection point O. At the moment `t = 0` the ships were located at the distances 120 m and 200 m from the point O. How soon will the distance between the ships become the shortest and what is it equal to ?
View SolutionA particle at origin starts towards positive direction of x-axis, with an accelerationa. This acceleration can be defined in three ways,(a) `a =` constant, (b) `a = f(x)`, and (c) `a = -f (t)`. Find the velocity of the particle as a function of time. Also find velocity of the particle when it is at a displacement x from origin. Given that the velocity of the particle at `t = 0` is `v = w`.
View SolutionA driver travelling at 90 kph applied the brakes for 5 s. If the braking acceleration was `2 m//s^(2)`, what was her final speed ?
View SolutionA slowly moving flat car is 12.0 m long passing apoint at straight road at 10 kph. A boy beside the road near to that point tosses rocks onto the moving flat car at the rate of one per second, (a) If the first rock just hits the front edge of the car, how many rocks will fall on to that car ? (b) How many rocks will fall onto that car if the car begins to accelerate at `0.5 m//s^(2)`, just as the first rock hits the car ?
View SolutionIn a car race, `A` takes a time of `t` s, less than car `B` at the finish and passes the finishing point with a velocity `v` more than car `B`. Assuming that the cars start from rest and travel with constant accelerations `a_(1)` and `a_(2)`. Respectively, show that `v=sqrt(a_(1) a_(2)t)`.
View SolutionTwo bodies start moving in the same straight line at the same instant of time from the same origin. The first body moves with a constant velocity of `40ms^-1`, and the second starts from rest with a constant acceleration of `4ms^-2`.Find the time that elapses before the second catches the first body. Find the also the greatest distance between them prior to it and time at which this occurs.
View SolutionA driver travelling at 30 kph sees the light turn red at the intersection. If his reaction time is 0.6s , and the car can decelerate at `4.5 m//s^(2)`, find the stopping distance ofthecar. What would the stopping distance be ifthe car were moving at 90 kph.
View SolutionIf body travels half of its path in the last second of its fall from rest, find the time and height of its fall.
View SolutionA person sitting on the top of a tall building is dropping balls at regular intervals of one second. Find the positions of the 3rd, 4th and 5th ball when the 6th ball is being dropped.
View SolutionA small parachute dropped from a 30 m high cliff falls freely under gravity for 1.0 s and then attains a trminal velocity 1.2m/s. 20.0 s latera stone is dropped from the cliff. Will the stone catch up with the parachute before it reaches the ground ?
View SolutionA balloon is going up with a uniform speed 20 m/s. It was at a height of 100 m from ground, when a stone is dropped from its basket. Find the time taken by the stone to reach the groimd and the height of the balloon from the ground, when stone hits the ground. (Take `g = 10 m//s^(2)`)
View SolutionFrom the foot of a tower 90m high, a stone is thrown up so as to reach the top of the tower. Two second later another stone is dropped from the top of the tower. Find when and where two stones meet (Take `g = 10 m//s^(2)`)
View SolutionA girl is standing in an elevator that is moving upward at a velocity of `5m//s` and acceleration `2 m//s^(2)`, when she drops her handbag. If she was originally holding the bag at a height of 1.5 m above the elevator floor, how long will it take the bag to hit the floor
View SolutionA truck starts from rest with an acceleration of `1.5 m//s^(2)` car 150 m behind starts from rest with an acceleration of `2 m//s^(2)`. How long will it take before both the truck and car side byside, and how much distance is traveled by each?
View SolutionAn elevator car whose floor to ceiling distance is equal to `2.7m` starts ascending with constant acceleration `1.2 m//s^2.` 2 s after the start, a bolt begins falling from the ceiling of the car. Find
(a)the time after which bolt hits the floor of the elevator.
(b)the net displacement and distance travelled by the bolt, with respect to earth. (Take `g=9.8 m//s^2)`
View SolutionConsider the child standing on the top of a tower of height h, shown in figure-l .12. He throws the ball up and the ball follows the trajectory as shown in figure. Draw the displacement versus time graph of the ball's motion during its flight. Take vertically upwards direction as positive x-axis.

View SolutionDraw, the velocity - time graph for the case explained in example 1.21.
View SolutionA car starts moving rectilinearly first with acceleration `alpha=5 m s^(-2)` (the initial velocity is equal to zero), then uniformly, and finally, deceleration at the same rate `alpha` comes to a stop. The time of motion equals `t=25 s`. The average velocity during this time is equal to `
72 kmh^(-1)` How long does the car move uniformly?
View SolutionA car accelerates from rest at a constant rate ` alpha ` for some time after which it decelerates at a constant rate ` beta` to come to rest. If the total time lapse is ` t` seconds , evauate.
(i) maximum velocity reached , and
(ii) the total distance travelled .
View SolutionInstantaneous velocity of a particle moving in astraight line is given as `v = (4 + 4 sqrtt) m//s`. For the first five second of motion. Then after velocity of it becomes a constant. Find the acceleration of the particle at time t = 3.0 s and its displacement till this instant.
View SolutionInstantaneous velocity of an object varies with time as `v = alpha - beta t^(2)`. Find its position and acceleration as a function of time, also find the object's maximum positive displacement from the origin.
View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as `v=alphasqrtx`, where `alpha` is a positive constant. Assuming that at the moment `t=0` the particle was located at the point `x=0`, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View SolutionA point moves rectilinearly with deceleration which depends on the velocity v of the particle as `a = k sqrtv`, where is apositive constant. At the initial moments the velocity of the point is equal to `v_(0)`. What distance will it cover before it stops, and what time it will take to cover that distance.
View SolutionAn object moves such that is acceleration is given as `a = 3 - 2t`. Find the initial speed of the object such that the particle will have the same x-coordinate at `t = 5.0`s as it had at `t = 0`. Also find the object's velocity at `t = 5.0s`.
View SolutionA man standing on a road has to hold his umbrella at `30^(@)` with the vertical to keep the rain away. He throws the umbrella and starts running at 10km/hr. He finds that rain drop are hitting his head vertically. Find the speed of rain drops with respect to (a) road (b) the moving man.
View SolutionA `400 m` wide river is flowing at a rate of `2.0 m s^-1`. A boat is sailing with a velocity of `10 m s^-1` with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View SolutionTwo trains, one travelling at 54 kph and the ot her at 72kph, are headed towards each ot her on a level track. When the yare two kilometers apart, both drivers simultaneously apply their brakes. If their brakes produces equal retardation in both the trains at a rate of `0.15 m//s^(2)`, determine whether there is a collision or not
View SolutionA boat moves relative to water with a velocity `v` which is `n` times less than the river flow velocity `u`. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionOn morning Joy was walking on a grass-way in a garden.Wind was also blowing in the direction of his walking with speed `u`.He suddenly saw his friend Kim walking on the parallel grass-way at a distance `x` away.Both stopped as they saw each other when they were directly opposite on their ways at a distance `x`.Joy shouted "Hi Kim".Find the time after which Kim would have heard his greeting.Sound speed in still air is `v`.
View SolutionTwo swimmers leave point A on the bank of the river to reach point B lying right across on the other bank. One of them crosses the river along the straight line AB while the other swims at right angles to the stream and then walks the distance that he has been carried away by the stream to get to point B. What was the velocity u of his walking if both swimmers reached the destination simultaneously? The stream velocity `v_0=2.0 km//hour` and the velocity `v^'` of each swimmer with respect to water equals to `2.5km` per hour.
View SolutionA particle is moving in XY plane such that its velocity in x-direction remains constant at `5 m//s` and its velocity in y-direction varies with time as `v = 3 t m//s`, where t is time in seconds. Find :
View SolutionA car starts moving from rest on a horizontal ground such that the position vector of car with respect to its starting point is given as `vec(r) = b t hat(i) - c t^(2) hat(j)`, where a and b are position constants, direction (x and y axes) intersect at the starting point of car (origin). Find:
(a) The equation of the trajectory of car `y = f(x)`.
(b) The angle between direction of velocity and acceleration of car as a function of time `theta = f (t)`.
(c) Average velocity of car over first t seconds of motion
View SolutionA point moves in the plane `xy` according to the law `x=at`, `y=at(1-alphat)`, where a and `alpha` are positive constants, and t is time. Find:
(a) the equation of the point's trajectory `y(x)`, plot this function,
(b) the velocity v and the acceleration w of the point as functions of time,
(c) the moment `t_0` at which the velocity vector forms an angle `pi//4` with the acceleration vector.
View SolutionA projectile is thrown from a point on ground with an initial speed u and at anelevatio `theta` to the horizontal. Find the change in momentum of the particle, when it reaches the top most point of its trajectory.
View SolutionWhen a particle is projected at an angle to the horizontal, it has range R and time of flight `t_(1)`. If the same projectile is projected with same speed at another angle to have the saem range, time of flight is `t_(2)`. Show that:
`t_(1)t_(2)=(2R//g)`
View SolutionTwo second after projection, a projectile is travelling in a direction inclined at `30^(@)` to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of the velocity of projection.
View SolutionA cannon fires successively two shells from the same point with velocity `V_(0)=250m//s`, the first at the angle `theta_(1)=60^(@)` and the second at the angle `theta_(2)=45^(@)` to the horizontal, the azimuth being the same. Neglecting the air drag, find the approximate time interval between firings leading to the collision of the shells `(g=9.8m//s^(2))`
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If `alpha and beta` be the base angles and `theta` the angle of projection, prove that `tan theta = tan alpha + tan beta` .
View SolutionA stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
View SolutionThe radius of the front and rear wheels of a carriage are a and b, and c is the distance between the front an drear axles. A particle of dust driven from the highest point of the rear wheel is observed to alight on the highest point of the front wheel. Find the velocity of the carriage.
View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle `alpha` with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ?
View SolutionA projectile is thrown at an angle `theta` with an inclined plane of inclination `beta` as shown in fig. 1E108. Find the relation between `beta` and `theta` ifv :
(a)projectile strikezs the inclined plane perpendicularly,
(b) projectile strikes the inclined plane horizontal.
View SolutionA child throws a ball so as to clear a wall of heigh than data distance x from it. Find the minimum speed required for clearing the wall.
View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity u. As a result of this, end A starts moving down along the wall. Find the velocity of the other end B downward when the rod makes an angle `theta` with the horizontal.

View SolutionIn the arrangement shown in fig the ends `P` and `Q` of an unstretchable string move downwards with unifrom speed `U`. Pulleys `A` and `b` are fixed. Mass `M` move upwards with a speed

View SolutionFigure-1.52 showns a hemisphere and a supported rod. Hemisphere is moving in right direction with a uniform velocity `v_(2)` and the end of rod which is in contact with ground is moving in left direction with a velocity `v_(1)`. Find the rate at which the angle `theta` is changing in terms of `v_(1), v_(2)`, R and `theta`.
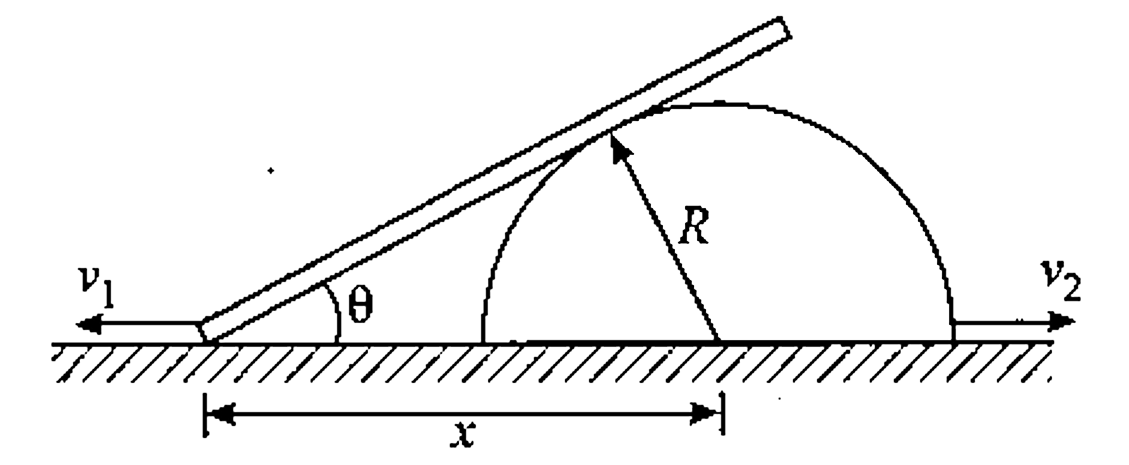
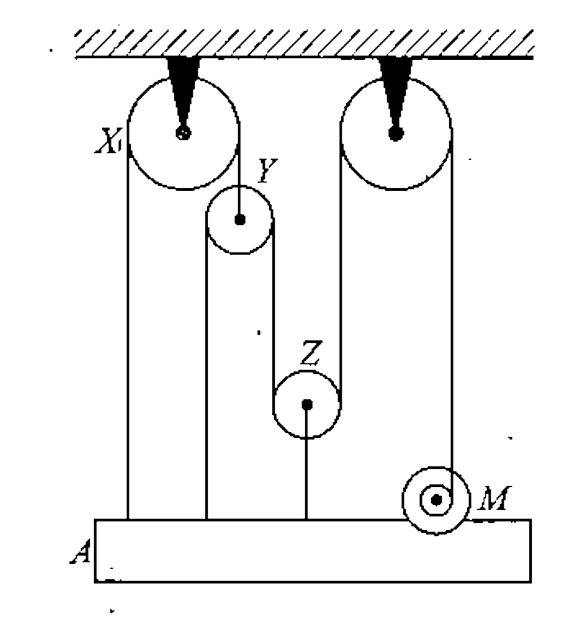
View SolutionConsider the situation of block pulley arrangement shown in figure-1.63. A plank is connected to three strings and an electric motor M is fitted on to it and a string is wound on it according to the arrangement shown in figure. Given that the string is winding on shaft of motor at a speed v. Find the speed with which the plank would be going up.
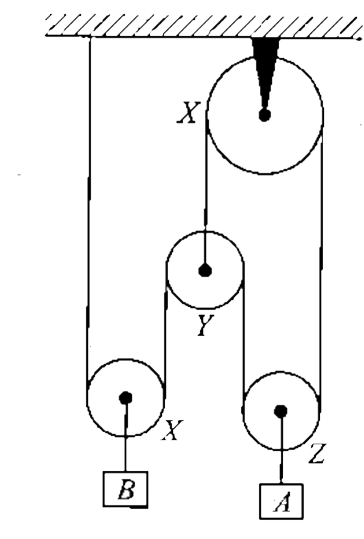
View SolutionFigure-1.65 shows a system of four pulleys with two masses A and B. Find, at an instant:
View SolutionConsider the situation shown in figure-l.76 (a) Find the constraint relation for velocities of blocks A and B.
View SolutionConsider the situation shown in figure-1.77 (a). A string connected to block B is passing through two movable pulleys X and Yand wound on the smaller disc of a step pulley. Another block A attached to the puIley X. Analyze the constrained motion of blocks A and B. (Step pulley radii ratio `= 1 : 3`)
View SolutionIf block B shown in figure-l.78(a) is going down with acceleration `5 m//s^(2)`, find the acceleration of the block A. All pulleys and strings are ideal. Radii ratio for the two step pulleys are `1 : 3 : 5` and `1 :2`.
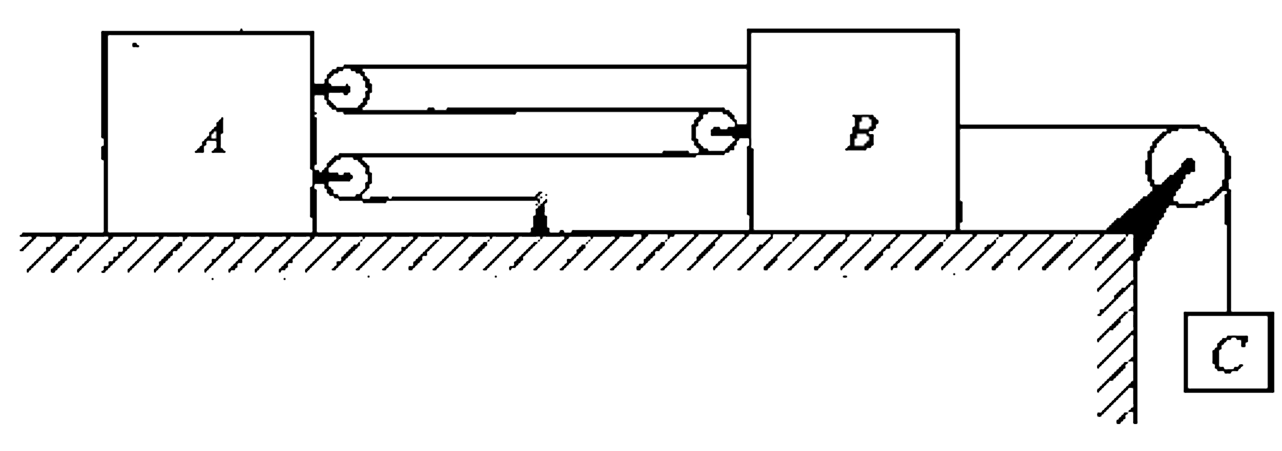
View SolutionBlock C shown in figure-1.79 is going down at acceleration `2 m//s^(2)`. Find the acceleration of blocks A and B.
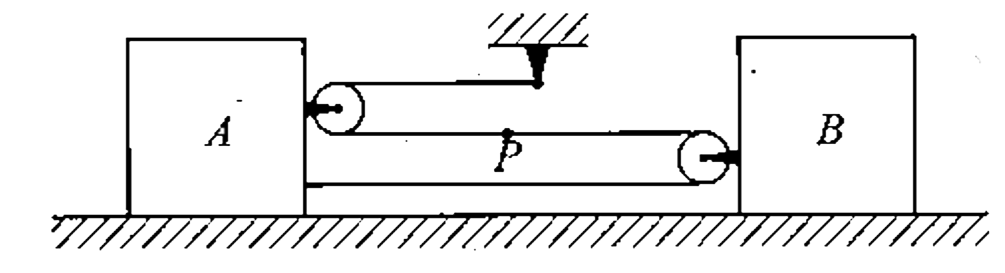
View SolutionBlocks shown in figure-1.81 move by a distance 3 m toward left. Find the distance and direction in which the point P on string shown in figure is displaced.
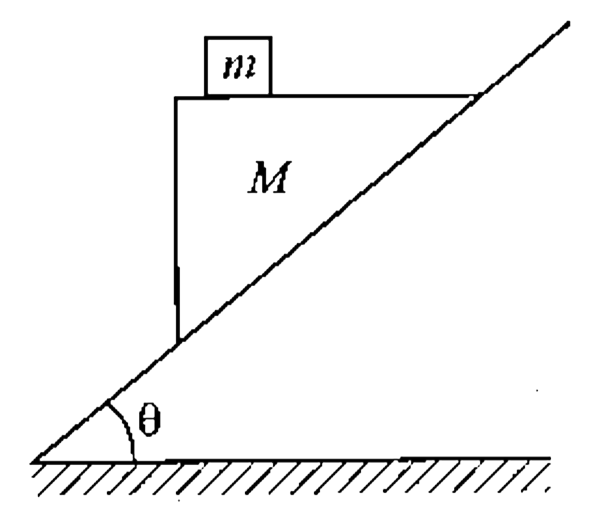
View SolutionIn the situation shown in figure-1.86, if mass M is going down along the incline at an acceleration of `5 m//s^(2)` and m is moving toward right relative to M horizontally with `3 m//s^(2)`. Find the net acceleration of m
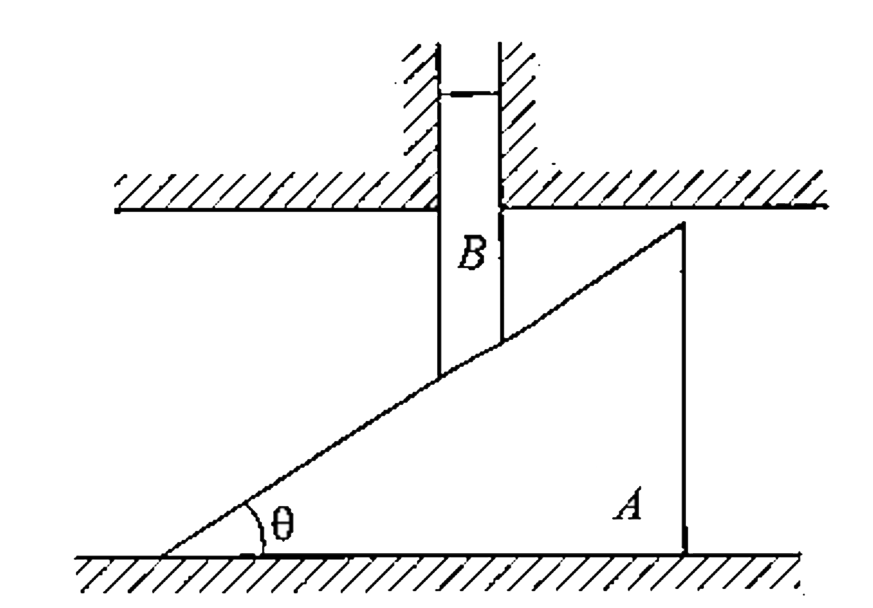
View SolutionFind the relation among accelerations of wedge A and the rod B supported on wedge A. Rod B is restricted to move vertically by two fixed wall comers shown in figure-1.88.
View SolutionFigure shows a block A constrained to slide along the inclined plane of the wedge B shown. Block A is attached with a string which passes through three ideal pulleys and connected to the wedge B. If wedge is pulled toward right with an acceleration a, find
(a) the acceleration of the block with respect to wedge
(b) the acceleration of the block with respect to ground.

View Solution
Illustrative Example questions and complete solutions for chapter KINEMATICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11