Complete Solutions to Unsolved Numerical Pro. of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PHYSICS GALAXY | Unsolved Numerical Pro. |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
A ball is released from rest. If it takes 1 second to cross the last 20 m before hitting the ground, find the height from which it was dropped.
View SolutionThe accelerator of a train can produce a uniform acceleration of `0.25ms^(-2)` and its brake can produce a retardation of `0.5ms^(-2)` The shortest time in which the train can travel between two stations 8 km apart is x minutes and 10 s, if it stops at both stations. The value of x is.
View SolutionAll insect is moving on a groove whose displacement is given `x = 6t^(2) - 8+40.cos pi t`, , where x and t are expressed in metres and seconds. Find the position, velocity and acceleration of insect at time t = 6 s.
View SolutionTwo cars, A and B, are traveling in the same direction with velocities `v_(a)` and `v_(b)` respectively. When car is at a distance d behind car B, the brakes on A are applied, causing a deceleration at a rate a. Show that to prevent a collision between A and B it is necessary that:
View SolutionA motor boat starts from rest with an acceleration given by the law `a = (c)/((x+4)^(2))` where c is a positive constant. Given that the velocity of the boat when its displacement is `8 m` is `4m//s`. Find:
(a) The magnitude of c .
(b) The position of the boat when its speed was 4.5 m/s.
(c) The maximum velocity of the boat.
View SolutionThe acceleration of a particle is given by the relation as `a = -kv^(5//2)` , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View SolutionIn a given steam jet, the velocity of the steam at the mouth of jet is `V_(0) = 3.6 m//s`. The velocity of the steam at a distance x from jet is given as `v = (0.18v_(0))/(x)`. Find the acceleration of the air at X=2 m and the time required for the air to flow from x = 1m to x = 3m
View SolutionFigure shows three blocks A, B and C connected by a cable and system of pulleys. The blocks is pulled downward with a constant velocity of `7.5 cm//s`. At t = 0 , block, A starts moving downward from rest with a constant acceleration. It is given that the velocity of block A after travelling 20 cm is 30cm/s, find the change in position, velocity and the acceleration of block C at this instant.
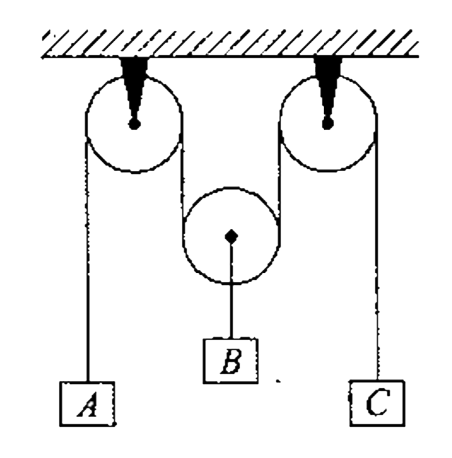
View SolutionA traffic police officer observes a fast moving car. Due to over speed officer starts his bike, accelerates uniformly to 90 kph in 8 s, and maintaining a constant velocity of 90 kph, overtakes the car 42 s after the car passed him. If he overtakes the carafter 18 s from the instant he starts, find the distance the officer travelled before overtaking and the speed of car.
View SolutionA steel ball is dropped from the roof of a building. `A` man standing in front of a `1-m` high window in the building notes the the ball takes `0.1 s` to the fall from the top to the bottom of the window. The ball continues to fall and strikes the ground. On striking the ground, the ball gets rebounded with the same speed with which it hits the ground. If the ball reappears at the bottom of the window `2 s` after passing the bottom of the window on the way down, find the height of the building.
View SolutionA particle starts from a pointn A and travels along the solid curve shown in figure. Find approximately the position B of the particle such that the average velocity between the positions A and B has the same direction as the instantaneous velocity at B.

View SolutionA car starts moving along a line, first with acceleration a=5 `ms^(-2)` starting from rest then uniformly and finally decelerating at the same rate a, comes to rest.The total time of motion is `tau=25 s`. The average velocity during the time is equal to lt v gt =72 km/hr.How long does the partial move uniformly ?
View SolutionIn a motorcycle race, a rider A is leading another rider B by 36 m and both riders are travelling at a constant speed of 170 kph. At t=0 both starts accelerating at a constantrate. It is given that after 8s, So vertakes And at this instant speed of A is 220 kph. Find the accelerations of the two riders
View SolutionTwo friends A and B are standing a distance x apart in an open field and wind is blowing in a direction perpendicular to .the line joining AB. A beats a drum and finds a time lag between seeing and hearing the drum beating by A. Find this time lag.
View SolutionTwo blocks A and B are shown in figure. Block A moves to the left with a constant velocity of 6m/s. Find :
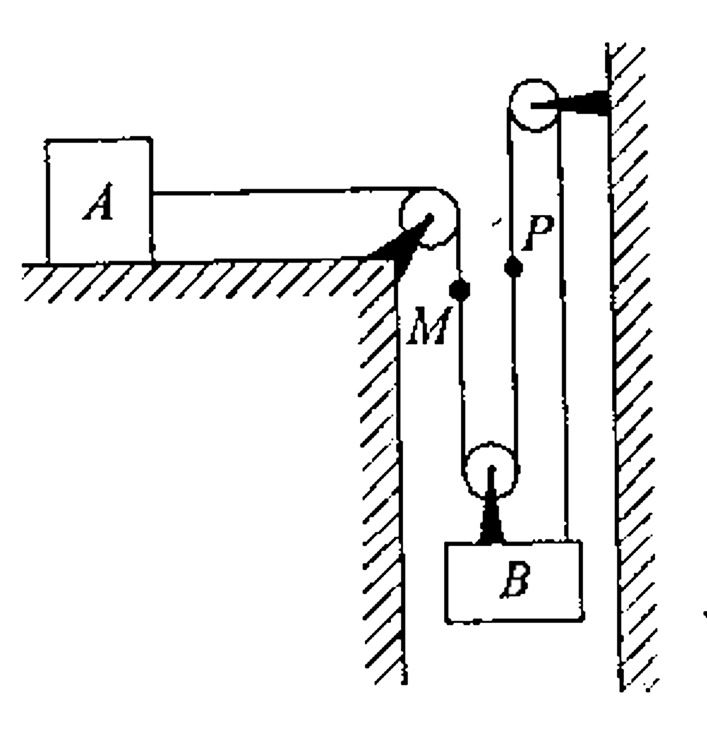
(a) Velocity of the blocks B.
(b) Velocity of the point P of the string.
Relative velocity of the point M of the cable with respect to the point P.
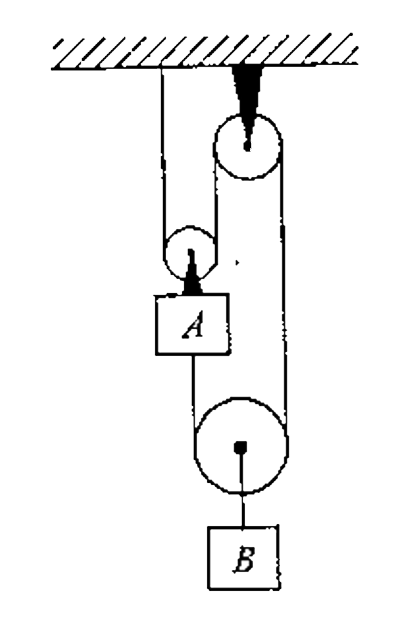
View SolutionIn figure block A starts from rest and moves upward with a constant acceleration. After 8 s the relative velocity of block B with respect to A is 0.6 m/s. Find the accelerations of blocks A and B. Also find the velocity of block B after 6 s.
View SolutionA man of height 1.2 m walks away from a lamp hanging at a height of 4.0 m above ground level. If the man walks with a speed of `2.8 m//s`, determine the speed of the tip of man's shadow.
View SolutionA particle moves in a straight line with the velocity curve shown in figure. Draw approximate acceleration vs time and displacement vs time curves. Consider x=0 at `t = 0`.
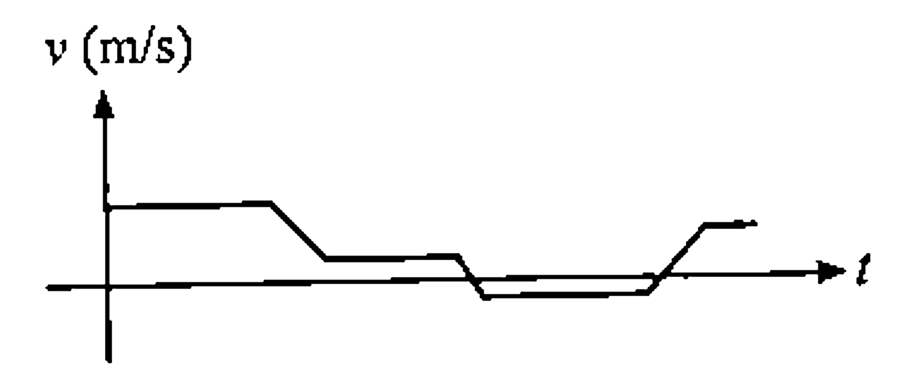
View SolutionA point mass starts moving in a straight line with a constant acceleration a. At a time `t_(1)` a fter the beginning of motion, the acceleration changes sign, remaining the same in magnitude. Determine the time t from the beginning of motion in which the point mass returns to the initial position.
View SolutionA car `C_(1)` travelling at a uniform speed of 75 kph passed another `C_(2)` car at rest beside the track. Two minutes later `C_(2)` starts and accelerates uniformly until its speed increases to 100 kph, then it maintains the speed. After 12 minutes from the instant `C_(1)` passes `C_(2)`, `C_(2)` is 800 m ahead of `C_(1)`. Find when and where `C_(2)` overtakes `C_(1)` and the acceleration of `C_(2)`.
View SolutionA helicopter takes off along the vertical with an acceleration `a = 3m//s^(2)` and zero initial velocity. In a certain time the pilot switches off the engine. At the point of take off, the sound dies away in a time `t_(2) = 30 sec`. Determine the velocity of the helicopter at the moment when its engine is switched off assuming that velocity of sound is 320 m/s.
View SolutionTwo trucks are moving in a straight line towards each other at initial velocities `u_(1)` and `u_(2)` and with constant retardations `a_(1)` and `a_(2)`. If the initial separation between them is `d`, find the minimum value of `d` for no collision.
View SolutionBlock 5 shown in figure moves to the right with a constant velocity of 30 cm/s. Find :

(a) The velocity of block A.
(b) The velocity of the point P of the string.
(c) The velocity of the point M of the string.
(d) The relative velocity of the point P of the string with respect to the block A.
View SolutionAt t = 0, block B in figure starts moving with a velocity 15 cm/s and with a constant acceleration. It is observed that after blocks travels 24 cm to the right its velocity is 6cm/s. Find:
(a) The accelerations of A and B,
(b) The acceleration of point M of the string.
View SolutionA stone is dropped from the top of a cliff of height h. ''n'' seconds later, a second stone is projected downwards from the same cliff with a vertically downward velocity u. Show that the two stones will reach the bottom of the cliff together, if
`8h(u-gn)^(2) = gn^(2)(2u - gn)^(2)`
what can you say about the limiting value of ''n'' ?
View SolutionHow long will a plane take to fly around a square with side a with the wind blowing at a velocity u, in the two cases (a) the direction of the wind coincides with one of the sides (b) the direction of the wind coincides with one diagonal of the square. The velocity of the plane in still air is `v gt u`..
View SolutionThe motion of an in secton at able is given as `x = 4t-2 sin t` and `y = A-1 cos t`, where x and y are in metres and t is in seconds. Find the magnitude of minimum and maximum velocities attained by the insect.
View SolutionTwo motor cars start from A simultaneously & reach B after 2 hour. The first car travelled half the distance at a speed of `v_(1)=30 km hr^(-1)` & the other half at a speed of `v_(2)=60 km hr^(-1)`. The second car covered the entire with a constant acceleration. At what instant of time, were the speeds of both the vehicles same? Will one of them overtake the other enroute?
View SolutionA body of mass m is thrown straight up with a velocity Mq. Find the velocity u' with which the body comes down if the air drag equals `cu^(2)` where c is a constant and u is the velocity of the body.
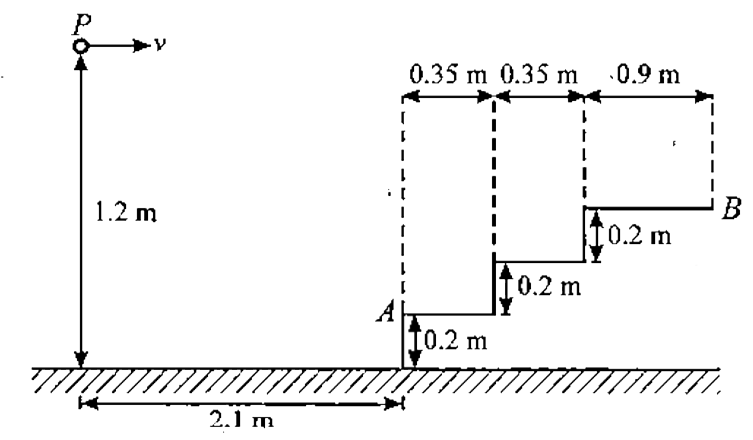
View SolutionIn a village Shyam bats for hitting two points A and B on a staircase with his goli from the position P shown in figure. Find the velocities required for P to hit A and B.
View SolutionA ship moves along the equator to the east with velocity `v_0=30km//hour`. The southeastern wind blows at an angle `varphi=60^@` to the equator with velocity `v=15km//hour`. Find the wind velocity `v^'` relative to the ship and the angle of `varphi^'` between the equator and the wind direction in the reference frame fixed to the ship.
View SolutionPoint A moves uniformly with velocity `nu` so that the vector `v` is continually "aimed" at point B which in its turn moves rectilinearly and uniformly with velocity `upsilon lt nu`. At the initial moment of time `v_|_u` and the points are separated by a distance `l`. How soon will the points converge?
View SolutionThe speed of a train increases at a constant rate `alpha` from zero to v and then remains constant for an interval and finally decreases to zero at a constant rate `beta`. The total distance travelled by the train is l. The time taken to complete the journey is t. Then,
View SolutionThe position vector `vec(r)` of a moving particle at time t after the start of the motion is given by `vec(r) = (5+20t)hat(i) + (95 + 10t - 5 t^(2)) hat(j)`. At the t = T, the particle is moving at right angles to its initial direction of motion. Find the value of T and the distance of the particle from its initial position at this time.
View SolutionOn a cricket field, the batsman is at the origin of coordination and a fielder stands in position given as `(46 hat(i) + 28 hat(j))m`. The batsman hits the ball so that it rolls along the ground with constant velocity given `(7.5 hat(i) + 10 hat(j))m//s`. The fielder can run with a speed of `5m//s`. If the starts to run immediately the ball is hit, what is the shortest time in which he could intercept the ball.
View SolutionTwo steel balls fall freely on an elastic slab. The first ball is dropped from a height `h_(1)` and the second from a height `h_(2)(h_(2) lt h_(1)) sec` after the first ball. After the passage of time T, the velocities of the balls coincide in magnitude and direction. Determine the time T and the time interval during which the velocities of the two balls will be equal assuming that the balls do not collide.
View SolutionA motor boat, with its engine on in a running river and blow n over by a horizontal wind is observed to travelat 20 kph in a direction `53^(@)` East of North. The velocity of the boat with its engine on in still water & blown over by the horizontal wind is 4kph East ward and the velocity of the boat with its engine on over the running river, in the absence of wind is 8 kph due south. Find:
(a) The velocity of the boat in magnitude and direction, over still water in the absence of wind.
(b) The velocity of the wind in magnitude and direction.
View SolutionA particle moves from rest in a straight line with alternate acceleration and retardation of mahnitudes `f` and `f'` during equal intervals of time `t`. At the end of `2n` such intervals prove that the space it has described is
`(n t^(2))/(2) [(2n + 1) f - (2 n - 1)f']`
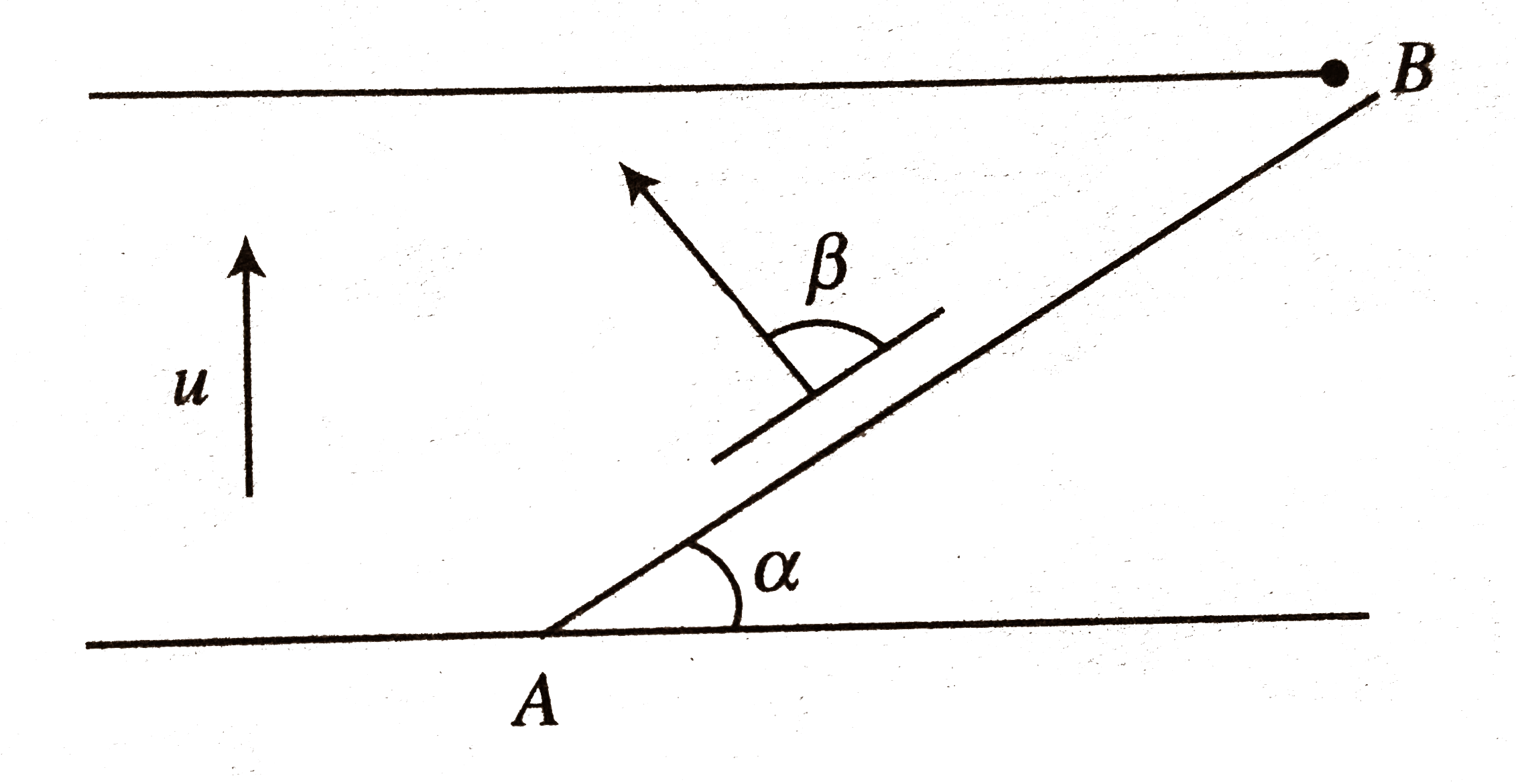
View SolutionA launch travels across a river from a point `A` to a point `B` of the opposite bank along the line `AB` forming angle `prop` with the bank. The flag on the mast of the launch makes an angle `beta` with its direction of motion. Determine the speed of the launch w.r.t. the bank. The velocity of wind is `u` perpendicular to the stream.
 .
.
View SolutionA particle moves for total time T sec in a straight line in three consecutive parts such that its acceleration during the first, second and third parts is in the ratio 1:2:7. The distances covered in the first and the third parts are a and b meters while the time taken for each of the is tseconds. Find the average velocity of the particle during the second part.
View SolutionTwo particles are located on a horizontal plane at a distance `60 m`. At `t = 0` both the particles are simultaneously projected at angle `45^@` with velocities `2 ms^-1 and 14 m s^-1`, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
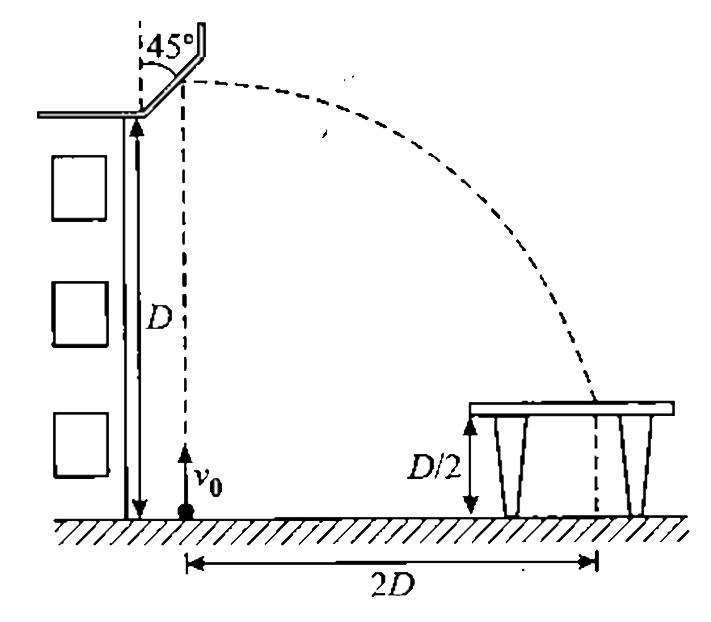
View SolutionA ball is projected directly upward with an initial speed `v_(0)`. Bounces elastically from a roof inclined at an angle `45^(@)` as shown in figure and then it strikes a table at a horizontal distance 2D from its starting point. Find `v_(0)`.
View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value `v_0` in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
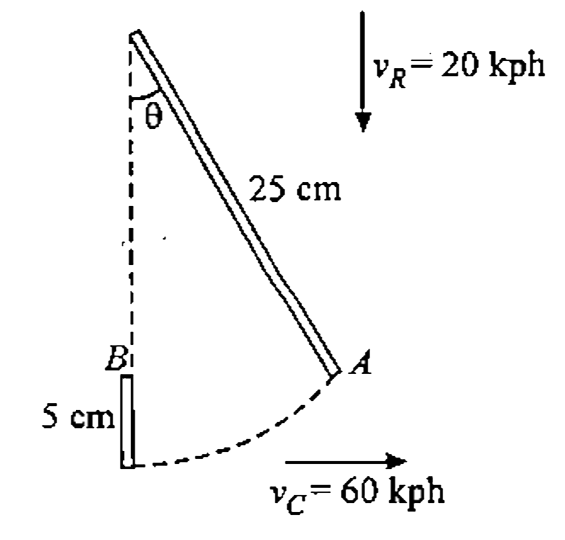
View SolutionA vertical wind screen of a car is made up of two parts, as shown in figure, where the upper one A is 25cm vertically long and covers the 5cm of the lower piece B.The upper one is hinged at the top so that it can be opened outward, inclining to the vertical. The car is running on the horizontal road at 60km/hr in the rain which is falling vertically at 20km/hr. Find the maximum angle, through which the upper part A can be opened outward, such that the rain drops do not enter the car.
View SolutionA hunter is riding an elephant of height `4 m` moving in straight line with uniform speed of `2m//sec`. A deer running with a speed `V` in front at a distance of `4sqrt(5)` moving perpendicular to the direction of motion of the elephant. If hunter can throw his spear with a speed of `10m//sec`. relative to the elephant, then at what angle `theta` to it's direction of motion must he throw his spear horizontally for a successful hit. Find also the speed 'V' of the deer.
View SolutionA swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle `theta` with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
View SolutionTwo particles, 1 and 2, move with constant velocities `v_1` and `v_2`. At the initial moment their radius vectors are equal to `r_1` and `r_2`. How must these four vectors be interrelated for the particles to collide?
View SolutionA ball is thrown from ground level so as to just clear a wall 4m high at a distance of 4 m and falls at a distance of 14 m from the wall. Find the magnitude and direction of the initial velocity.
View SolutionA bomber plane is moving horizontally in a straight line with speed 594 km//hour. When the fighter is 300 m behind, he fires guns which are then horizontal. If the bullets have a muzzle velocity of `3348 km//"hour"` relative to the fighter at what distance below the line of slight and at what angle will the bullet hit the bomber ? Neglect air resistance and wind effects. Given that the velocity of the fighter plan is 720 km/hour.
View SolutionA man in a river boat must get from point `A` to point `B` on the opposite bank of the river (see figure).The distance `BC=a`.The width of the river `AC=b`.At what minimum speed `u` relative to the still water should the boat travel to reach the point `B`?The velocity of flow of the river is `v_(0)`

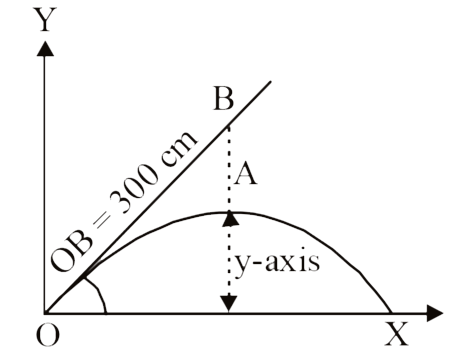
View SolutionA ball 'A' is projected from origin with an initial velocity `v_(0)` = 700 cm/sec in a direction `37^(@)` above the horizontal as shown in fig .Another ball 'B' 300 cm from origin on a line `37^(@)` above the horizontal is released from rest at the instant A starts. How far will B have fallen when it is hit by A ?
View SolutionAn Aeroplane flies horizontaily at a height h at a speed v. An anti-air craft gun fires a shell at the plane when it is vertically above the gun. Show that the minimum muzzle velocity required to hit the plane is `sqrt(v^2+2gh)` at an angle `tan^(-1)((sqrt(2gh))/(v))`
View SolutionA ball is projected at an angle of `30^(@)` above with the horizontal from the top of a tower ans strikes the ground in `5sec` at angle of `45^(@)` with the horizontal. Find the hieght of the lower and the speede with which it was projected.
View SolutionTwo boys simultaneously aim their guns at a bird sitting on a tower. The first boy releases his shot with a speed of 100m/s at an angle of projection of `30^(@)` . The second boy is ahead of the first by a distance of 50 m and releases his shot with a speed of 80m/s. How must he aim his gun so that both the shots hit the bird simultaneously ? What is the distance of the foot of the tower from the two boys and the height of the tower ? With what velocities and when do the two shots hit the bird?
View SolutionA boy throws a ball up ward with a speed of 12m/s The wind imparts a horizontal acceleration of `0.4 m//s^(2)`. At what angle `theta` to the vertical, the ball must be thrown so that it returns to the point of release.
View SolutionA student is standing on the open platform of a moving trains at a speed of `10m//s`. The student throws a ball into the air along a path that the, he judges to make an initial angle of `60^(@)` with the horizotal and to be in line with the track. The professor, who is standing on the ground nearby, observes the ball to rise vertically. Find the height reached by the ball.
View SolutionOn a two lane road , car (A) is travelling with a speed of `36 km h^(-1)`. Tho car ` B and C` approach car (A) in opposite directions with a speed of ` 54 km h^(-1)` each . At a certain instant , when the distance (AB) is equal to (AC), both being ` 1 km, (B) decides to overtake ` A before C does , What minimum accelration of car (B) is required to avoid and accident.
View SolutionA particle moves in the plane x y with constant acceleration a directed along the negative y-axis. The equation of motion of the particle has the form `y = k_(1)x-k_(2)x^(2)`, where `k_(1)` and `k_(2)` are positive constants. Find the velocity of the particle at the origin of coordinates.
View SolutionA gardener shower jet is placed at a distance d from the wall of a building. If R is the maximum range of the jet that is produced when the bowl is connected to the nose of a fire engine, show that the portion of the wall that is hit by the jet of water is bounded by a parabola whose height is `((R^(2)-d^(2)))/(2R)` and breadth is `2sqrt(R^(2)-d^(2))`.
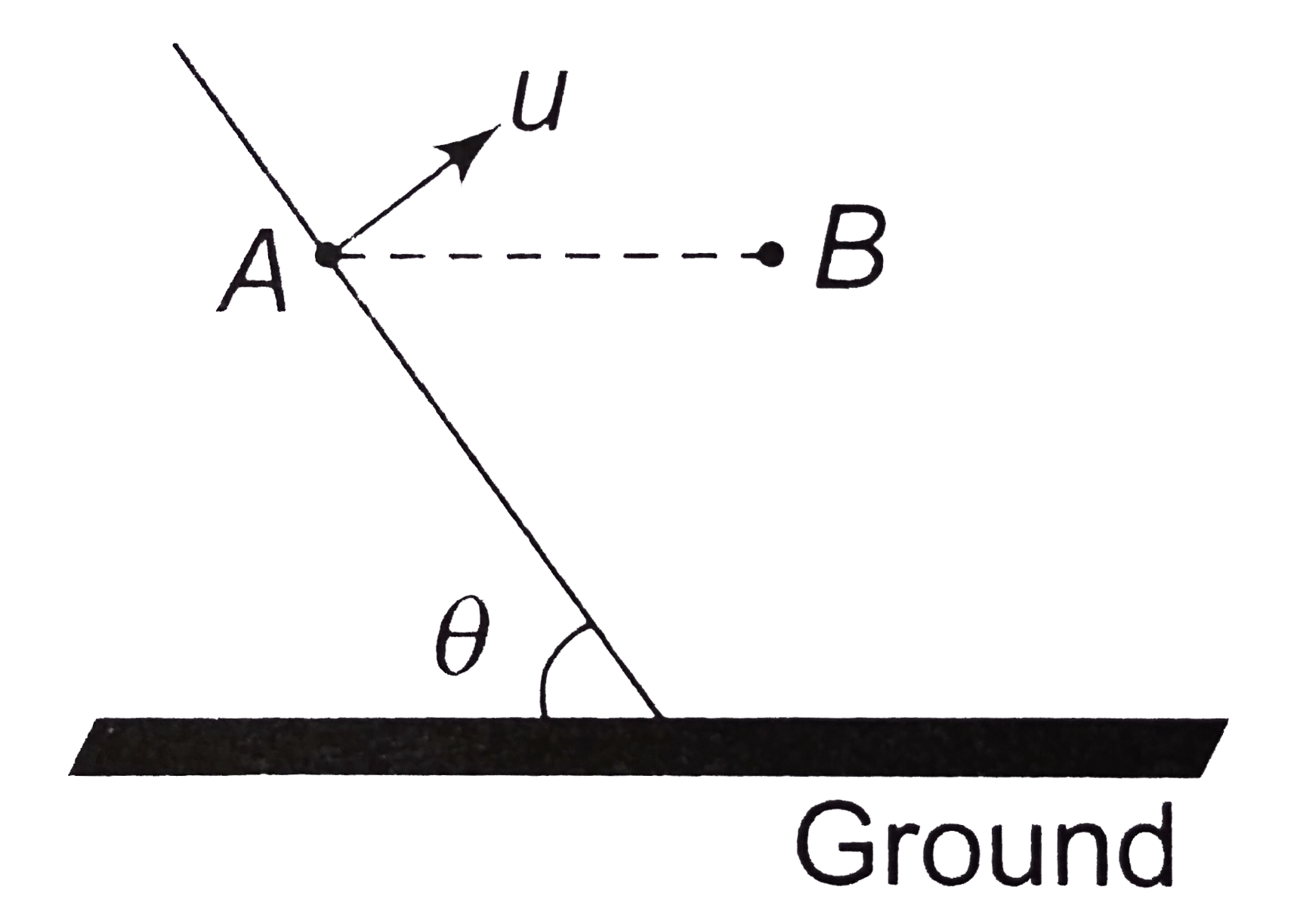
View SolutionA particle is projected at point A from an inclination plane with inclination angle `theta` as shown in figure. The magnitude of projection velocity is `vecu` and its direction is perpendicular to the plane. After some time it passes from point B which is in the same horizontal level of A, with velocity `vecv`. Then the angle between `vecu and vecv` will be
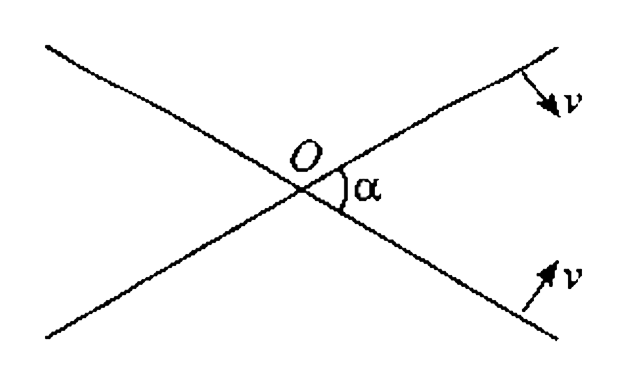
View SolutionTwo lines AB and CD intersect at O at an inclination `alpha`, as shown in figure. If they move out parallel to themselves with the speed v, find the speed of O.
View SolutionA gun of muzzle speed `v_(0)` is situated at height h above a horizontal plane. Prove that the angle at which it must be fired so as to achieve the greatest range on the plane is given by-
`theta = (1)/(2)cos^(-1) ((gh)/(v_(0)^(2)+gh))`
View SolutionA shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is `prop = 30^@` and the angle of the barrel to the horizontal `beta = 60^@`. The initial velocity `v` of the shell is `21 m s^-1`. Then find the distance of point from the gun at which the shell will fall.
View SolutionA particle is projected on an inclined plane with a speed `u` as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA projectile aimed at a mark, which is in the horizontal plane through the point of projection, falls a cm short of it when the elevation is `alpha` and goes b cm far when the elevation is `beta`. Show that, if the speed of projection is same in all the cases the proper elevation is
`1/2 sin^(-1) [(bsin2alpha+asin2beta)/(a+b)]` .
View SolutionA boy sitting at the rear end of a railway compartment of a train, running at a constant acceleration on horizontal rails throws towards the fore end of the compartment with a muzzle velocity of 20m/sec at an angle `37^(@)` above the horizontal, when the train is running at a speed of 10 m/sec. If the same boy catches the ball without moving from his seat and at the same height of projection,find the speed of the train at the instant of his catching the ball.
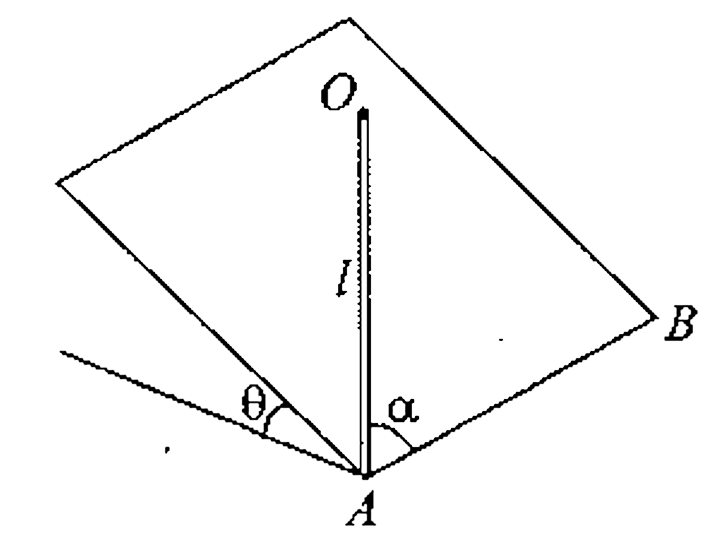
View SolutionThere is an inclined surface of inclination `theta`. A smooth groove is cut into it forming an angle `alpha` with AB as shown in figure. A steel ball is free to slide a long the groove. If the ball is released from the point O. Find the speed when it comes to A.
View SolutionTo a person travelling due East with velocity u the wind appears to blow from an angle `alpha` North of East. When he starts travelling due North with velocity 2 u,the wind appears to blow from an angle `beta` North of East. Find the true direction of the wind.
View SolutionA guided missile is fired to strike an object at the same level 38 km away. It may be assumed that it rises vertically 1.5 km and then for the remainder of the flight it follows a parabolic path at an elevation of `45^(@)` . Calculate its velocity at the begining of its parabolic path.
View SolutionA train takes 2 minutes to acquire its full speed 60 kph from rest and 1 minute to come to rest from the full speed. If some where in between two stations 1 km of the track be under repair and the limited speed on this part be fixed to 20 kph, find the late running of the train on account of this repair work, assuming otherwise normal at running of the train between the stations.
View SolutionA stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
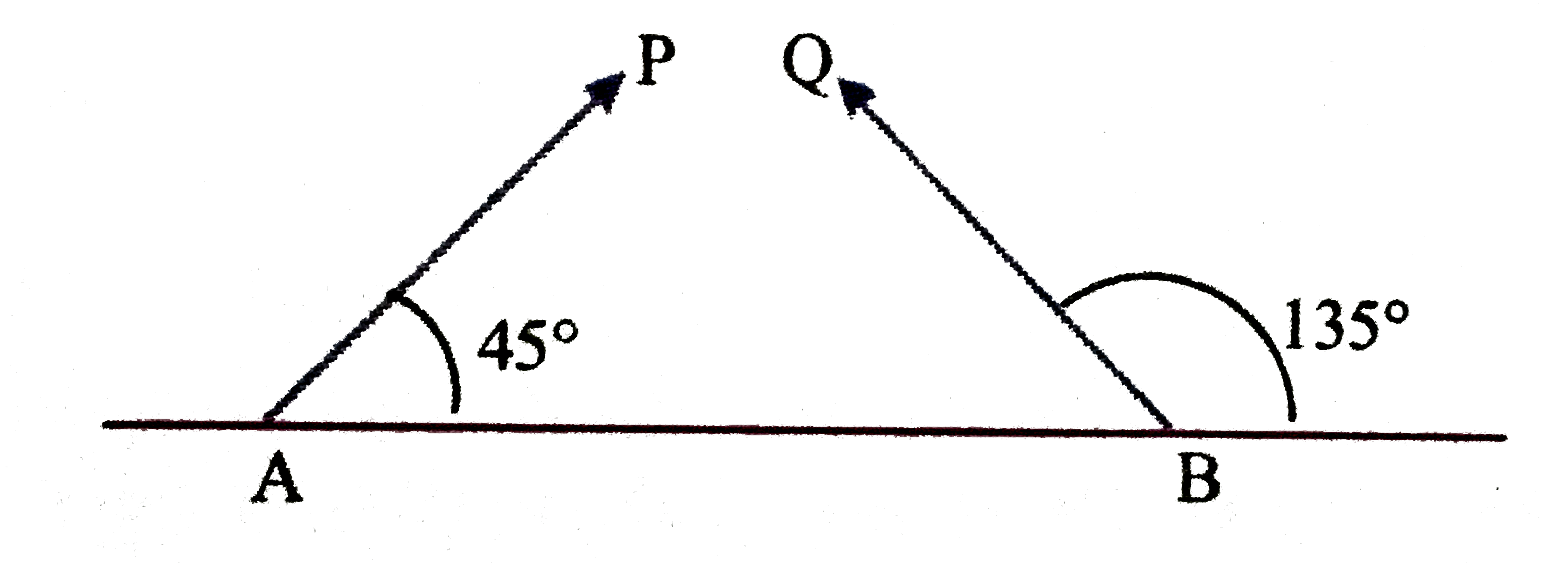
View SolutionParticles `P` and `Q` of masses `20g` and `40g`, respectively, are projected from positions `A` and `B` on the ground. The initial velocities of `P` and `Q` make angles of `45^(circ)` and `135^(circ)`, respectively with the horizontal as shown in the fig. Each particle has an initial speed of `49m//s`. The separation `AB` is `245m`. Both particles travel in the same vertical plane and undergo a collision. After the collision `P` retraces its path. The separation of `Q` from its initial position when it hits the ground is
View SolutionTwo shots are projected from a gun at the top of a hill with the same velocity u at angles of projection `alpha` and `beta` respectively. If the shots strike the horizontal ground through the foot of the hill at the same point, show that the height h of the hill above the plane is given by :
`h = (2u^(2)(1-tan alpha tan beta))/(g(tan alpha+tan beta)^(2))`
View SolutionA point moves in the plane `xy` according to the law `x=a sin omegat`, `y=a(1-cos omega t)`, where a and `omega` are positive constants. Find:
(a) the distance s traversed by the point during the time `tau`,
(b) the angle between the point's velocity and acceleration vectors.
View SolutionTwo towers AB and CD are situated at a distance d apart, as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown fromt the top of CD at an angle of `60^(@)` to the horizontal towards AB with the same magnitude of initial velocity as that oft he first object. The two objects move in the same vertical plane, collide in mid air and stick to each other (i) calculate the distance between the towers and (ii) find the position where the objects hit the ground.

View SolutionA particle moves uniformly with speed v along a parabolic path `y = kx^(2)`, where k is a positive constant. Find the acceleration of the particle at the point x = 0.
View SolutionA bullet of mass M is fired with a velocity `50m//s` at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length `10//3` metres and gets embeded in the bob. After the collision, the string moves through an angle of `120^@`. Find
(i) the angle `theta`,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take `g=10 m//s^2`
View SolutionTwo bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle `alpha` with the horizontal. Both the bodies have velocity equal to `u`. Find the separation between the bodies at time `t`.
View SolutionA particle is moving in a plane with velocity `vec(v) = u_(0)hat(i) + k omega cos omega t hat(j)`. If the particle is at origin at `t = 0`, (a) determine the trajectory of the particle. (b) Find its distance from the origin at `t = 3pi//2 omega`.
View SolutionTwo swimmers start a race. One who reaches the point `C` first on the other bank wins the race.`A` makes his strokes in a direction of `37^(0)` to the river flow with velocity `5km//hr` relative to water. `B` makes his strokes in a direction `127^(0)` to the river flow with same relative velocity.River is flowing with speed of `2km//hr` and is `100m` wide.speeds of `A` and `B` on the ground are `8km//hr` and `6km//hr` respectively.

View SolutionTwo particles are simultaneously projected in the same vertical plane from the same point with velocities u and v at angles `alpha and beta` with horizontal. Find the time that elapses when their velocities are parallel.
View SolutionThree points are located at the vertices of an equilateral triangle whose sides equal to `a=3m`.They all start moving simultaneously with speed `v=1m//s`, with the first point heading continually for the second, the second for the third, and the third for the first.How soon will the points meet?
View SolutionA particle is projected up an inclined plane of inclination `beta` at na elevation `prop` to the horizontal. Show that
(a) `tan prop = cot beta + 2 tan beta`, if the particle strikes the plane at right angles
(b) `tan prop = 2 tan beta`, if the particle strikes the plane horizontally.
View Solution
Unsolved Numerical Pro. questions and complete solutions for chapter KINEMATICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11