Complete Solutions to Practice Exercise of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PHYSICS GALAXY | Practice Exercise |
| Number Of Questions | 96 |
| Academic Year | 2023-24 |
Two bicycle riders made a 30 km trip in the sametime. Cyclist A travelled non-stop at an average speed of 20 kph. Another cyclist B travelled with a lunch break of 20 min. What was the average speed of B for the actual riding ?
View SolutionThe light speed is `3.0 xx 10^(8) m//s`, and the sound speed is 340 m/s. Find the value of count N, if ''A child start counting after every second, he sees a bomb blast 1km away and stops when he hear its 'blast sound."
View SolutionTwo cars travelling in parallel lanes at 90 kph and 72 kph. Assuming each car to be 5 m long, find the time taken during the overtake and the total road distance used for the overtake
View SolutionA point traversed half of the total distance covered by its with velocity `v_0`.The remaining part of the distance was covered with velocity `v_1` for half of the remaining time, and with velocity `v_2` for the other half of the remaining time.Find the mean velocity of the point over the whole time of motion.
View SolutionFrom point A located on a highway (figure) one has to get by car as soon as possible to point B located in the field at a distance `l` from the highway. It is known that the car moves in the field `eta` times slower than on the highway. At what distance from point D one must turn off the highway?

View SolutionTwo junglemen are standing at the two opposite banks of a river of width `l` facing each other. One of the m starts beating a drum and sound reaches to the other one after time `t_(1)` the stats. Then second one starts beating the drum and now first one hear the sound after time `t_(2)`. Calculate the velocity of sound relative to air and the velocity of wind, if it is blowing from first bank to the other bank at right angle to the river flow
View SolutionA rectangular farm house has a `1km` difference between its sides. Two farmers simultaneously leave one of the vertex of the rectangle for a point at the opposite vertex. One farmer crosses the farmhouse along its diagonal and other walks along the edge. The speed of each farmer is `4km//hr`. If one of them arrives half an hour earlier then the other then the size of farmhouse is .
View SolutionA car is moving at a constant speed of 40 km/h along a straight road which heads towards a large vertical wall and makes a sharp `90^0` turn by the side of the wall. A fly flyingat constant speed of 100 km/h, starts from the wall towrds the car t an instant when the car is 20 km away,flies until it reaches the glasspane of the car and returns to teh wll at teh same speed. It continues to fly between the car and teh wall time the car makes the `90^0` turn. a. What is the total distance the fly has travelled during the period?b. How many trips has it made between the car and the wall?
View SolutionA bike starts from rest and accelerates at `4 m//s^(2)` for 5.0 s. It then moves at contant velocity for 25.0s, and then decelerates at `2.0 m//s^(2)` unit it stops. Find the total distance that the motorcycle has moved.
View SolutionFiate Siena can accelerate from 0 to 48 kph in 3.6s and from 0 to 96 kph in 10.2 s Also, under constant acceleration from rest it crosses the 0.4 km marker at as peed of 140 kph. (a)Calculate the average acceleration needed get the speed 48 kph. (b) Calculatethe average acceleration during the time it requires to go from 48 to 96 kph. (c) What constant acceleration would be required to get a speed of 140 kph over the 0.4 km run starting from rest ?
View SolutionTwo friends start bikes from one corner of as quarefield of edge L towards the diagonally opposite corner in the same time t: They both start from the same place and take different routes. One travels along the diagonal with constant acceleration a, and the other accelerates momentarily and then travels along the edge of the field with constant speed v. What is the relationship between a and v ?
View SolutionA truck travelling along a straight road at a constant speed of 72 kph passes a car at time `t = 0` moving much slower. At the instant the truck passes the car, the car starts accelerating at constant `1m//s^(2)` and overtake the truck 0.6 km further down the road, from where the car moves uniformly. Find the distance between them at time `t = 50 s`.
View SolutionA motorcycle and a car start from rest from the same place at the same and travel in the same direction. The motorcycle acceleration at `1.0 m s^(-1)` up to a speed of `36 km h^(-1)` and the car at `0.5 m s^(-1)` up to a speed of `54 km h^(-1)`. The time at which the car would overtake the motorcycle is
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionA point moving with constant acceleration from A to B in the straight line AB has velocities u and v at and B respectively. Find its velocity at C, the mid point of AB. Also show that if the time from A to C is twice that from C to B, then `v =7 u`.
View SolutionA train is targeted to run from Delhi to Pune at an average speed of 80 kph but due to repairs of track looses 2hr sin the first part of the journey. If then accelerates at a rate of `20 kph^(2)` till the speed reaches 100 kph. Its speed is now maintained till the end ofthe journey. If the train now reaches station in time, find the distance from when it started accelerating ?
View SolutionA train of length `l=350m` starts moving rectilinearly with constant acceleration `w=3.0*10^-2 m//s^2`, `t=30s` after the start the locomotive headlight is switched on (event 1), and `tau=60s` after that event the tail signal light is switched on (event 2). Find the distance between these events in the reference frames fixed to be train and to the Earth. How and at what constant velocity V relative to the Earth must a certain reference frame K move for the two events to occur in it at the same point?
View SolutionTwo cars travelling towards each other on a straight road at velocity `10 m//s` and `12 m//s` respectively. When they are 150 metre apart, both drivers apply their brakes and each car decelerates at `2 m//s^(2)` until it stops. How far apart will they be when they have both come to a stop?
View SolutionTwo bodies start moving in the same straight line at the same instant of time from the same origin. The first body moves with a constant velocity of `40ms^-1`, and the second starts from rest with a constant acceleration of `4ms^-2`.Find the time that elapses before the second catches the first body. Find the also the greatest distance between them prior to it and time at which this occurs.
View SolutionA ball is allowed to slip from restdown a smooth incline plane, and the distances are marked every 2.0 s. If the second mark is made 1.6 m from the starting point, where are the first and fourth marks ?
View SolutionWater drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take `g = 9.8 m//s^(2)`
View SolutionA particle is projected vertically upward from the ground at time `t = 0` and reaches a height `h` at `t = T`. Show that the greater height of the particle is `(g T^(2) + 2h)^(2)//8 gT^(2)`
View SolutionA circus artist maintains four balls in motion making each in turn to rise to a height of 5 m from hishand. Calculate the velocity with which he projects the balls. Where will the other three balls be at the instant when the fourth one is just leaving his hand ? Take `g = 10m//s^(2)`
View SolutionA dog sees a flowerpot sail upand then back down past a window 5 ft high. If the total time the pot is in sight is 1.0 sec, find the height above the window that the pot rises. Take `g = 32 ft//s^(2)`
View SolutionA ball projected vetically upwards from (A), the top of tower reaches the ground in ` t_1` second.
If it is projected vectically downwards from (A) with the same vecoty, it reaches the ground in ` t_2` seconds .
If it falls freely from (A), show that it would reahc the ground in ` sqrt t_1 t_2=2 seconds`.
View SolutionJimmy is doing an experiment to measure the height of a tall building. He drops awatermelon from the roof the building. 3.0 s later he hears the watermelon splash sound. What height of the building he had calculated. Take speed of soimd 340 m/s and air resistance, on water melon can be neglected. Take `g = 10 m//s^(2)`
View SolutionYou are on the roof of your school building 60m, high. You see your physics teacher 1.6 m tall walking directly towards the building at 2.m/s. You wish to throw an egg vertically down at a speed 5m/s on to your teacher's head. Where should your teacher be when you throw the egg. Neglect air resistance. Take `g = 10m//s^(2)`
View SolutionA student goes to the a 100 m high floor of Kutubmeenar at Delhi. To verify the law of gravity, he starts from a window with zero initial velocity, with a stop watch in his hand. After 3.0 s, Batman comes to the same floor and jumps to save the boy. What must be his initial velocity so that he'll just be able to save the boy. Assume free fall for both boy and Batman before he catches the boy. Take `g = 10m//s^(2)`
View SolutionFrom the top of at all building (height27.3m), a boy throws an apple upward, which strikes ground after 16 s. Take `g = 9.8 m//s^(2)`, find the speed of apple with which it was thrown and the maxium height reached by it.
View SolutionA roket fired vertically ascends with a constant acceleration `g//3` for `1 min`. Its fuel is then all used and it continues to rise as a free body. What is the maximum height reached? What is the total time elapsed from the take off until the rocket strikes the earth?
View SolutionA truck driver, starting with zero speed at time zero, drove in such a way that the speed time graph is approximately an isosceles triangle with the base along the time axis. The maximum speed was `30 m//s`, and the total elapsed time was 50.0 s. What distance did he travel.
View SolutionFigure-1.20 shows displacement-time graphof a particle. Find the time during motion such that the average velocity of the particle during that period is zero.

View SolutionA train starts from station `A` with uniform acceleration `a_(1)`. For some distance and then goes with uniform retardation `a_(2)` for some more distance to come to rest at station `B`. The distance between stations `A` and `B` is `4 km` and the train takes `1//5 h` to compete this journey. If accelerations are in km per minute unit, then show that `(1)/(a_(1)) +(1)/(a_(2)) =x`. Find the value of `x`.
View SolutionBetween two stations a train starting from rest first accelerates uniformly, then moves with constant velocity and finally retarts uniformly to come to rest. If the ratio of the time taken be `1 : 8 : 1` and the maximum speed attained be `60 km//h`, then what is the average speed over the whole journey ?
View SolutionA partical starts from rest and moves in a straight line. It travels a distance L with uniform acceleration and then moves with constant velocity a further distance `2L`. Finally, it comes to rest after moving a further distance 4L under uniform retardation. Find the ratio of average speed to the maximum speed.
View SolutionA particle starts with an initial velocity `u` towards `+ x` direction with an acceleration `a` after time `t_(1)`, it starts retarding with another acceleraation `a'`, comes to an instantaneous stop and returns. If reaches its initial position at time `t_(2)`. Draw the approximate time dependence plots for particle's displacement and velocity.
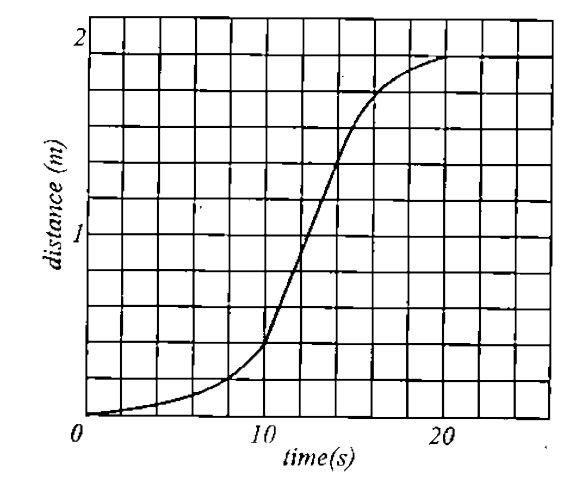
View SolutionA particle moves in a straight line. Figure-1.21 shows the distance traversed by the particle as a function of time `t`.Using the graph, find (a)the average velocity of the point during the time of motion, (b) the maximum velocity, (c) the time `t = t_(0)` at which the instantaneous velocity is equal to the mean velocity averaged over the first `t_(0)` seconds.
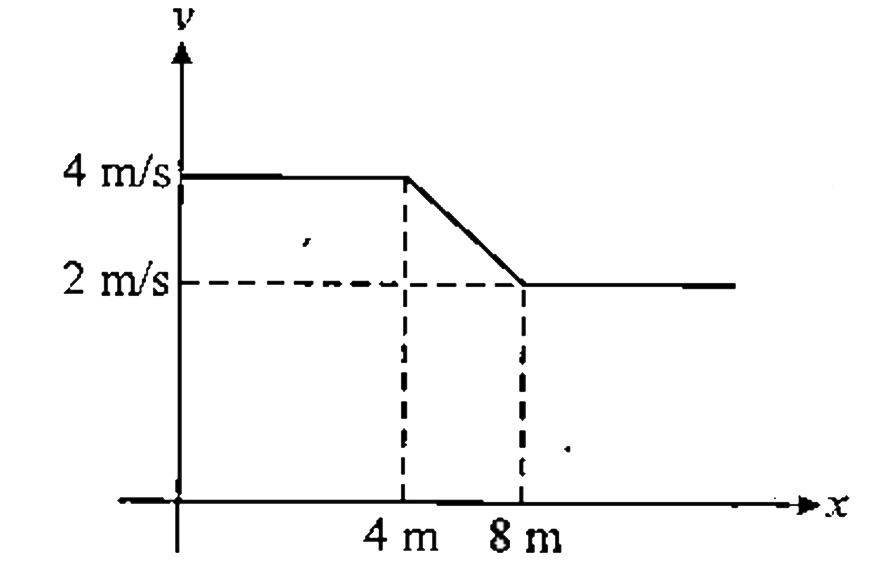
View SolutionThe velocityof a particle that moves in the positive X- direction varies with its position, as shown in figure-1.22. Find its acceleration in `m//s^(2)` where `x = 6m`
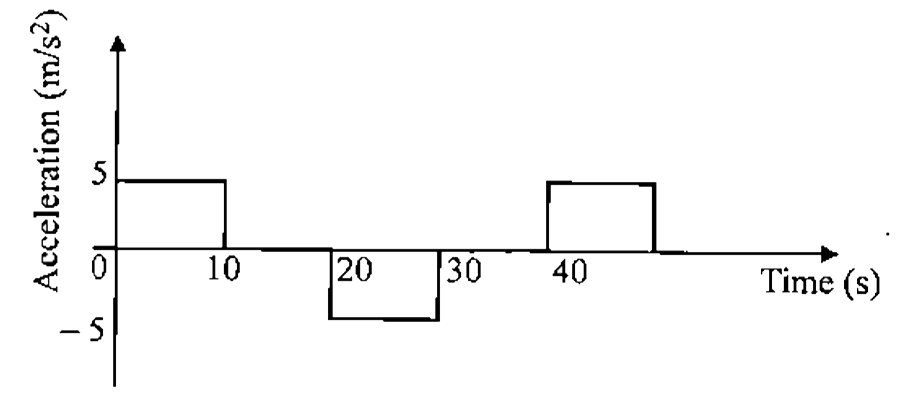
View SolutionThe acceleration vs time of a particle moving along `+x` direction is shown in figure-1.23. If starts at `t = 0`, from rest, Draw the position -time graph for the motion.
View SolutionThe displacement `x` of particle moving in one dimension, under the action of a constant force is related to the time `t` by the equation ` t = sqrt(x) +3`
where `x is in meters and t in seconds` . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first ` 6 seconds`.
View SolutionInstantaneous velocity of a particle moving in `+x` direction is given as `v = (3)/(x^(2) + 2)`. At `t = 0`, particle starts from origin. Find the average velocity of the particle between the two points `p (x = 2)` and `Q (x = 4)` of its motion path.
View SolutionA street car moves rectilinearly from station A to the next station B (from rest to rest) with an acceleration varying according to the law `f = a-bx,` where a and b are constants and x is the distance from station A. The distance between the two stations and the maximum velocity are
View SolutionA particle moves along a staight line such that its displacement at any time t is given by `s=t^3-6t^2+3t+4m`. Find the velocity when the acceleration is 0.
View SolutionA radius vector of a particle varies with time t as `r=at(1-alphat)`, where a is a constant vector and `alpha` is a positive factor. Find:
(a) the velocity v and the acceleration w of the particles as functions of time,
(b) the time interval `Deltat` taken by the particle to return to the initial points, and the distance s covered during that time.
View SolutionA box is thrown with velocity `v_(0)` on top of a rough table of length `l`. Assume friction on the object is such that during its motion, its acceleration is given as `a = -kv`, where `k` is a positive constant. Find the velocity of the box when it leaves the edge of the table. Also find the time after which it falls off the edge.
View SolutionA particle start revolution with initial speed `u` in a circular path of radius R. During revolution it is retarded due to friction and its acceleration is given as `a = cv^(2)`. Find the speed of the particle after completing one revolution.
View SolutionA rever `500 m` wide flows at a rate at a rate of `4 km h^(-1)`. A swinmmer who can swin at `8 km h^(-1)`. In still water, wishes to cross the river straight . (i) Along what direection must he strike? (ii) What should be his resultant velocity. (ii) What is the time of crossing the river?
View SolutionAn aeroplane takes off from Mumbai to Delhi with velocity 50 kph in north-east direction. Wind is blowing at 25 kph from north to south. What is the resultant displacement of aeroplane in 2 hrs.
View SolutionA man can swim at a speed of 3 km/h in still water. He wants t cross a 500 m wide river flowing at 2 km/h. He flow while swimming. A. Find the time he takes to cross the river. b.At what point on the opposite bank will he arrive?
View SolutionTwo boats, A and B, move away from a buoy anchored at the middle of a river along the mutually perpendicular straight lines: the boat A along the river, and the boat B across the river. Having moved off an equal distance from the buoy the boats returned. Find the ratio of times of motion of boats `tau_A//tau_B` if the velocity of each boat with respect to water is `eta=1.2` times greater than the stream velocity.
View SolutionA man running on the horizontal road at ` 8 km h^(-1)` find the rain appears to be falling vertically. He incresases his speed to `12 km h^(-1)` and find that the drops make angle ` 30^2` with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View SolutionTwo trains A and B are approaching each other on a straight track, the former with a uniform velocity of 25 m/s and other with 15m/s, when they are 225 m a part brakes are simultaneously applied to both of them. The deceleration given by the brakes to thetrain B increases linearly with time by `0.3 m//s^(2)` every second, while the train A is given a uniform deceleration, (a) What must be the minimum deceleration of the train A so that the trains do not collide ? (b) What is the time taken by the trains to come to stop ?
View SolutionA body starts from rest at A and moves with uniform accelerationa in a straight line. T seconds after,a second body starts from A and moves with uniform velocity Kinthe same line. Prove that the second body will be ahead of the first for a time `(2)/(a) sqrt(V (V - 2 aT))`
View SolutionAn aeroplane has to go from a point A to another point B, `500 km` away due `30^@` east of north. Wind is blowing due north at a speed of `20 m//s.` The steering-speed of the plane is `150 m//s.` (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go fram A to B.
View SolutionFind the time an aeroplane having velocity `v` takes to fly around a square with side `a` if the wind is blowing at a velocity `u` along one side of the square.\
View SolutionA man swimming in a river from a point. A on one bank has to reach a point C on other bank, which is at a distance `l` from the point B, directly opposite to A on other bank. River width is `d` and the current velocity is `u_(0)`. Find the minimum speed of swimmer relative to still water with which he should swim.
View SolutionThe coordinates of a bird flying in the `xy`-plane are `x = 2 - alpha t` and `y = beta t^(2)`, where `alpha = 3.6m//s` and `beta = 1.8 m//s^(2)`. Calculate 'the velocity and acceleration vectors and their magnitude as a functions of time .Also find the magnitude and direction of bird's velocity and acceleration at `t = 3.0s`. From the given data can you find whether at this instant, bird is speeding up, speeding down or it is taking a turn. If so in which direction
View SolutionOn a smooth horizontal platform a mass of 2 kg is dragged with a horizontal force of 10 Nt. On platform there are so many holes spreaded on its surface below which there is an air blower which exerts a force on block in upward direction depending on its height above the platformas `vec(F) = 20 (2 - h)N`, where h is the height of the block above the platform. Let at `t = 0` block starts from rest from origin of coordinate system shown. Find the equation of trajectory of the block during its motion. Consider x-axis along the motion ofparticle and y-axis in vertical up direction.
View SolutionA ball is thrown straight up in air with an initial velocity u. Air exerts a force on it in horizontal direction which produces an acceleration depending on its height from ground as `a_(x) = ah^(2)`. Find the displacement of ball from the projection point as a function of time.
View SolutionA boy releases a toy plane from the top of a high hill of height H. Hill is so high that gravity varies with height from ground as `g = g_(0) (1 - (2h)/(R))`, where h is the height from ground and R is the radius of earth. The engine of toy plane accelerates it in horizontal direction with acceleration `a_(x) = bt^(2)`. Find the position from the foot of hill where the plane lands and the time after which it lands.
View SolutionThe position vector of a particle P with respect to a stationary point O change with time according to the law `vec(r) = vec(b) sin omega t + vec(c) cos omega t` where `vec(b)` and `vec(c)` are constant vectors with `b pot c` and `omega` is a positive constant. Find the equation of the path of the particle `y = f (x)`, assuming x an dy axes to coincide with the direction of the vector `vec(b)` and `vec(c)` respectively and to have the origin at the point O
View SolutionThe motion of a particle restricted to move in a two dimensional plane is given by
`x = 2 cos pi t`
and `y = 1 - 4 cos 2 pi t`
where x and y are in metres and `t` is in seconds. Show that the path of the particle is a part of parabola `y = 5 - 2 x^(2)`. Find the velcoity and the acceleration of particle at `t = 0` and `t = 1.5 s`.
View SolutionA stone is thrown from the top of a tower of height 50 m with a velocity of 30 m per second at an angle of `30^(@)` above the horizontal. Find (a) the time during which the stone will be in air, (b) the distance from the tower base to where the stone will hit the ground, (c) the speed with which the stone will hit the ground, (d) the angle formed by the trajectory of the stone with the horizontal at the point of hit.
View SolutionA stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of `30^(@)` above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take `g = 10 m//s^(2)`
View SolutionTwo bodies are thrown at the same time and in opposite directions and with an equal velocity `v_(0)` at angles `alpha_(1)` and `alpha_(2)` to the horizon. What is the velocity with which the bodies move relative to each other -? What will be the distance between the bodies be after time t elapses ?
View SolutionA ball rolls off top of a staircase with a horizontal velocity `u m s^-1`. If the steps are `h` metre high and `b` mere wide, the ball will just hit the edge of `n th` step. Find the value of `n`.
View SolutionA boat is moving directly away from a gun on the shore with speed `v_(1)`. The gun fires a shell with speed `v_(2)` at anangle of elevation `alpha` and hits the boat. Prove that the distance of the boat from the gun at the moment it is fired is given by:
`(2v_(2) sin alpha)/(g) (v_(2) cos alpha - v_(1))`
View SolutionTwo bodies were thrown simultaneously from the same point, one, straight up, and the other, at an angle of `theta=60^@` to the horizontal. The initial velocity of each body is equal to `v_0=25m//s`. Neglecting the air drag, find the distance between the bodies `t=1.70s` later.
View SolutionTwo particles are projected from a point at the same instant with velocities whose horizontal and vertical components are `u_(1), v_(1)` and `u_(2), v_(2)` respectively. Prove that the interval between their passing through the other common point of their path is
`(2(v_(1)u_(2) - v_(2) u_(1)))/(g (u_(1) + u_(2))`
View SolutionA ball is thrown from a point in level with velocity `u` and at a horizontal distance `r` from the top os a tower of height `h`.
How must the speed and angle of the projection of the ball be related to `r` in order that the ball may just go grazing the top edge of the tower ?
View SolutionIn a "RamLeela"stage show an unhappy guy from audience throws an rotten egg at Rawana. The egg travels a horizontal distance of 15 m in 0.75 s before hitting the Rawana's face 1.7 m above the stage. The egg is thrown at 2.0 m above the horizonta floor with an initial velocity `30^(@)` above the horizontal, (a)Find the initial and final velocities of egg. (b)How high is the stage above the floor. Take `g = 10 m//s^(2)`
View SolutionA machine gun is mounted on the top of a tower of height h=100 m. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ?The muzzle speed of the bullet is `u=150 m s^(-1)` and `g=10 m s^(-2)` .
View SolutionA partacle is thrown in horizontal direction with speed u from a point P, the top of a tower shown in figure.1.49 at a vertical height `h` above the inclined plane of inclination `theta`. Find the speed with which the particle is thrown so that it strikes the plane normally. Also find the distance from the foot of the tower where the particle will strike.
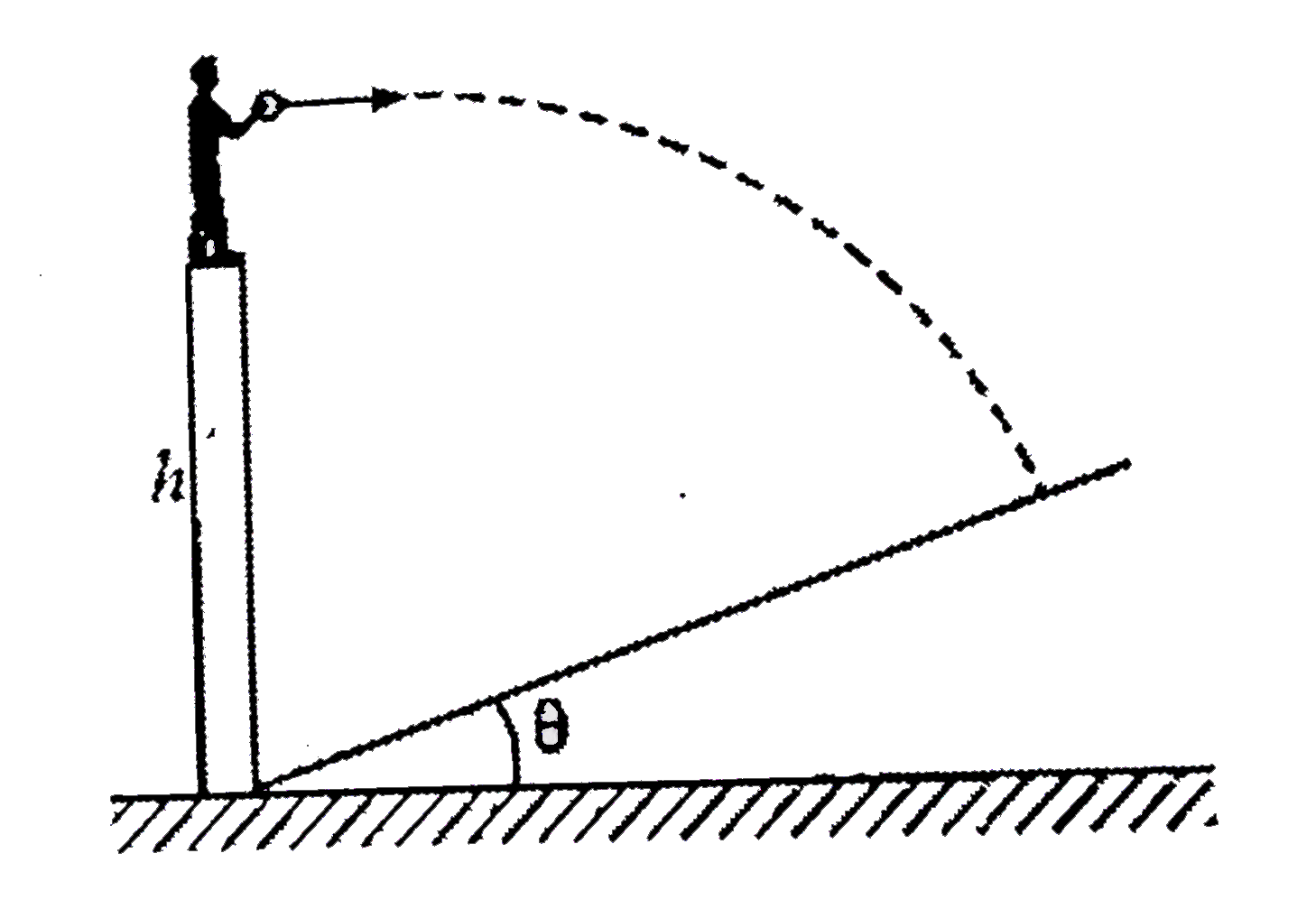
View SolutionFrom an inclined plane a particleis thrown in a direction normal to the surface. Find the ratio of successive ranges of the particle on inclined plane. Consider all collisions as elastic collisions (particle rebounds with the same speed with which it strikes the plane)
View SolutionA body is projected up with a speed `v_0` along the line of greatest slope of an inclined plane of angle of inclination `beta`. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.
View SolutionA partacle is thrown in horizontal direction with speed u from a point P, the top of a tower shown in figure.1.49 at a vertical height `h` above the inclined plane of inclination `theta`. Find the speed with which the particle is thrown so that it strikes the plane normally. Also find the distance from the foot of the tower where the particle will strike.

View SolutionIn example 1.49 find the velocity of the mid point of the rod in terms of its length l, v and `theta`.
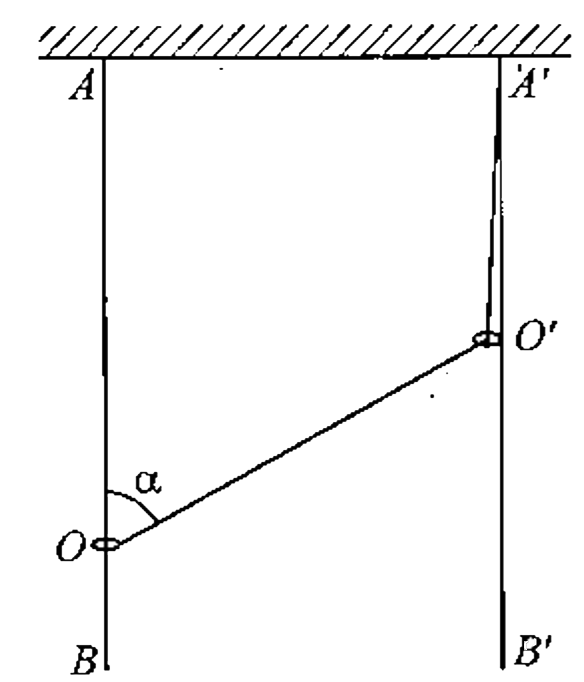
View SolutionTwo rings O and O' are put on two vertical stationary rods AB and A'B' respectively as shown in figure. An inextensible string is fixed at point A' and on ring O and is passed through O' moves downwards at a constant speed v, find the velocity of the ring O in terms of `alpha`.
View SolutionAn aircraft is descending to land at an airport in the morning. The aircraft is landing to the east, so that pilot has the sun in his eyes. The aircraft has a speed v and is descending at an angle `alpha` and the sun is at an angle `beta` above the horizon. Find the speed with which the aircraft's shadow moves over the groung.
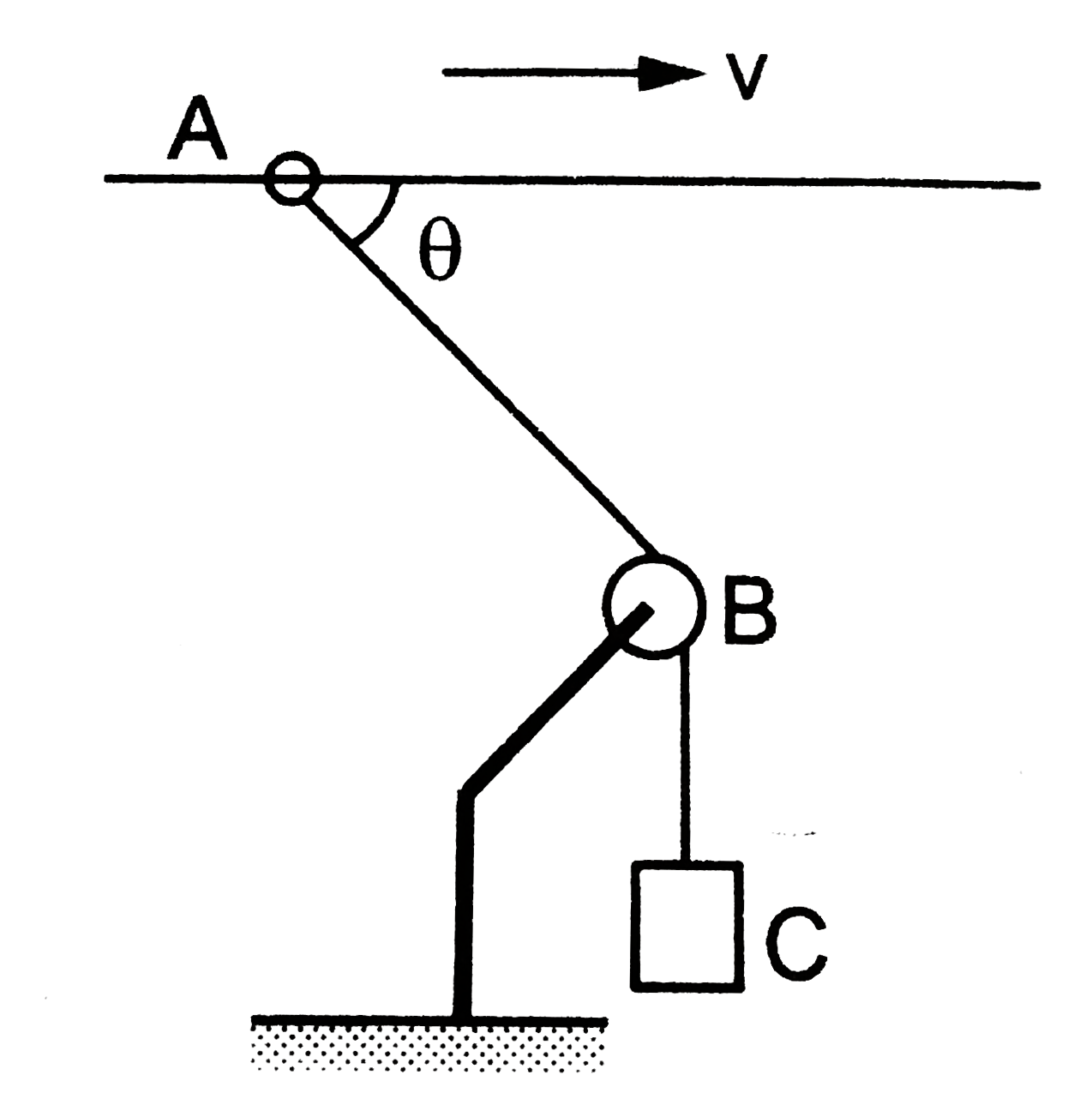
View SolutionFigure shows s small mass m hanging over a pulley. The other end of the thread is being pulled in horizontal direction with a uniform speed u. Find the speed with which the mass ascend at the instant the string makes an angle `theta` with the horizontal.

View SolutionA man of height 1.2 m walks away from a lamp hanging at a height of 4.0 m above ground level. If the man walks with a speed of `2.8 m//s`, determine the speed of the tip of man's shadow.
View SolutionFind the speed of the box-3, if box-1 and box-2 are moving with speeds `v_(1)` and `v_(2)` as shown in figure when the string makes an angle `theta_(1)` and `theta_(2)` with the horizontal at its left and right end.

View SolutionA smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of mass `M(=2m)` as shown in figure. At an instant the string between the ring and the pulley makes an angle `theta` with the rod. (a). Show that, if the ring slides with a speed v, the block descends with speed `v cos theta`, (b). With what acceleration will the ring starts moving if the system is released from rest with `theta= 30^0`
View SolutionFigure shows a pulley over which is string passes and connected to two masses A and B. Pulley moves up with a velocity `V_(P)` and mass B is also going up at a velocity `V_(B)`.

Find the velocity of mass A if
(a) `V_(P)=5ms^(-1)` and `V_(B)=10ms^(-1)`
(b) `V_(P)=5ms^(-1)` and `V_(B)=-20 ms_(-1)`.
View SolutionFind the relation in the accelerations of the three masses shown in fig.
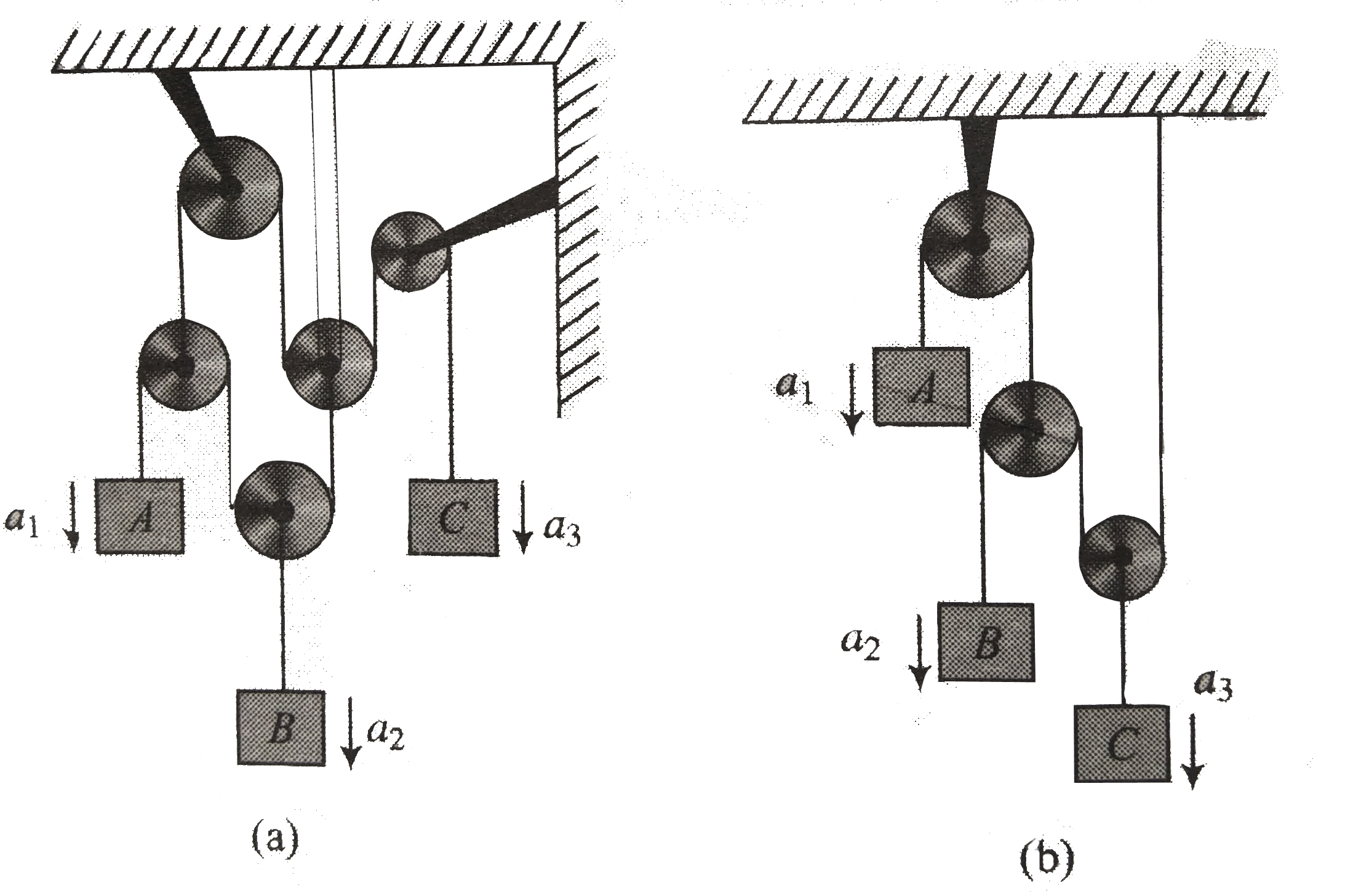
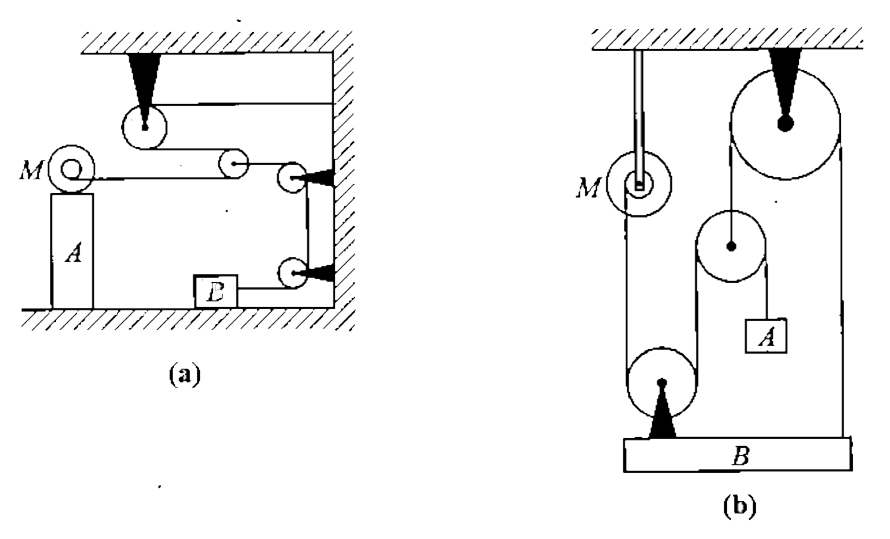
View SolutionFigure (a) and (b) shows a system of two masses A and B a motor M. find the relation in velocities of mass A and B, if the motor winding speed is v.
View SolutionFind the Relation among velocities of the blocks shown in figure (a), (b) moving under the given constraints.
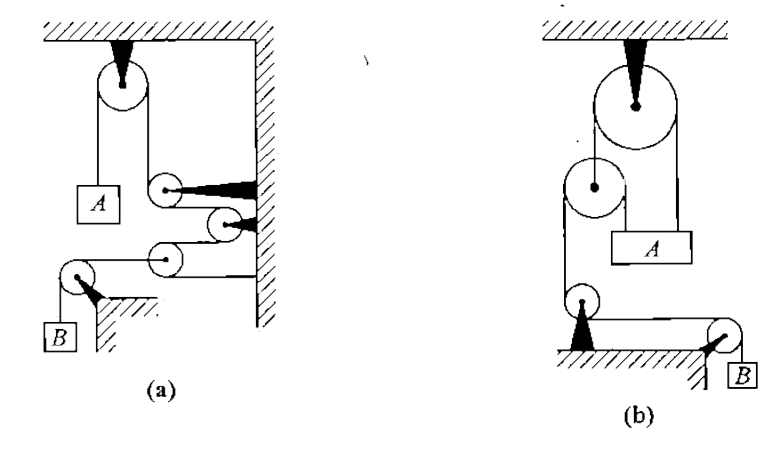
View SolutionBlock B shown in figure , moves downwards with a constant velocity of `20 cm//s`. At t = 0, block A is moving upward with a constant acceleration, and its velocity is `3cm//s`. If at `t = 3s` blocks C has moved 27 cm to the right, determine the velocity of block C at t = 0 and the acceleration of A and C.
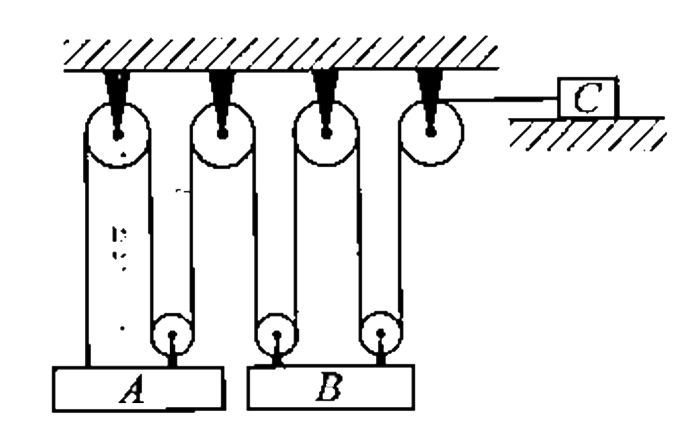
View SolutionBlock C shown in figure, starts from rest and moves downward with a constant acceleration. Knowing that after 12s the velocity of block A 7.2 m/s, determine the acceleration of A, B and C and the velocity and the displacement of block B after 8s.
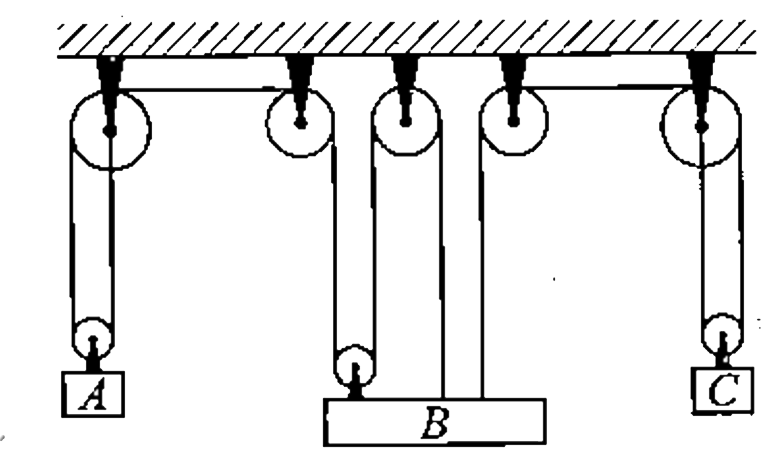
View SolutionThe system shown in figure starts from rest, and each block moves with a constant acceleration. If the relative acceleration of block C with respect to block B is `6m//s^(2)` upward and the relative acceleration of block D with respect to block C after 3s from starts.
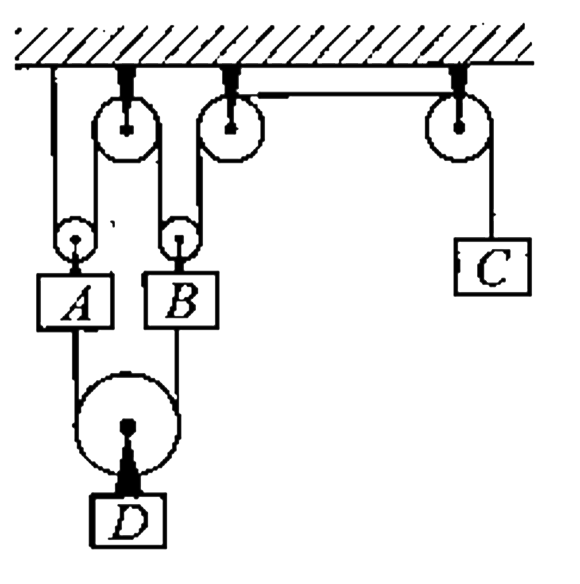
View SolutionFind the relation among the acceleration of blocks A and B constrained to move along the inclined surfaces of the fixed wedge shown in figure
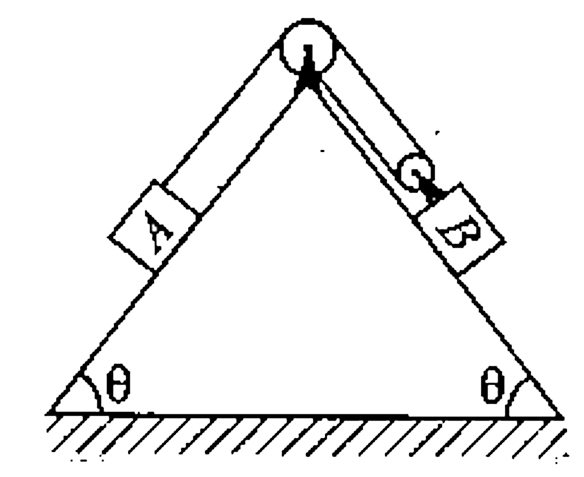
View SolutionIf the wedge A shown in figure-1.93, is moving toward left with acceleration `3 m/s^(2)`, find the net acceleration of block B which is constrainedtoslide along the wedge surface. `(theta=30^(@))`
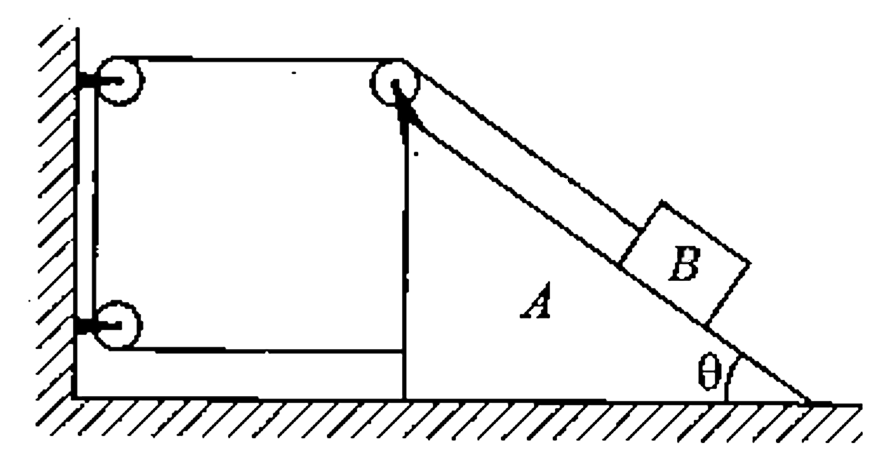
View SolutionFind the speed of the block B when the wedges A and C are moving toward each other with speed v and the strings connected to block make and angle `theta` with the vertical, as shown in figure
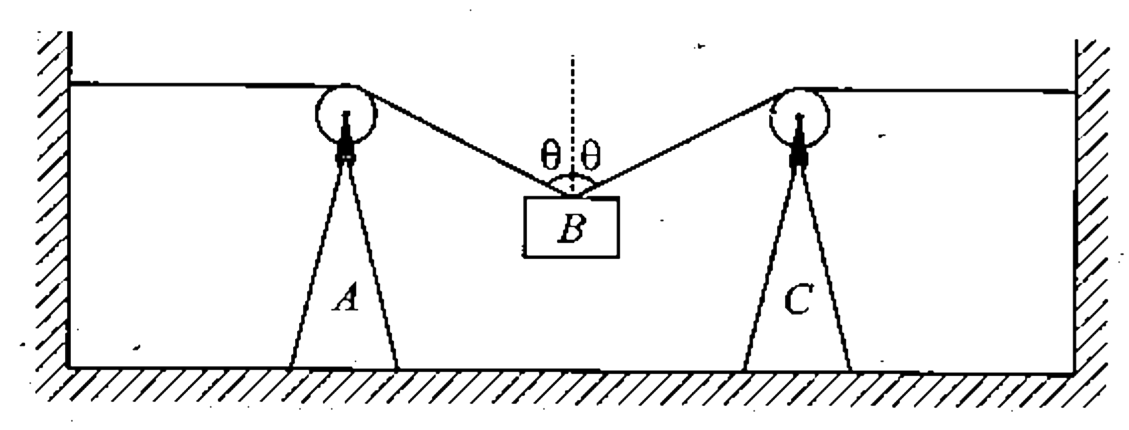
View SolutionFind the acceleration of the block B as shown in figure- 1.95 (a) and (b) relative to the block A and relative to ground if the block A is moving toward left with acceleration a.
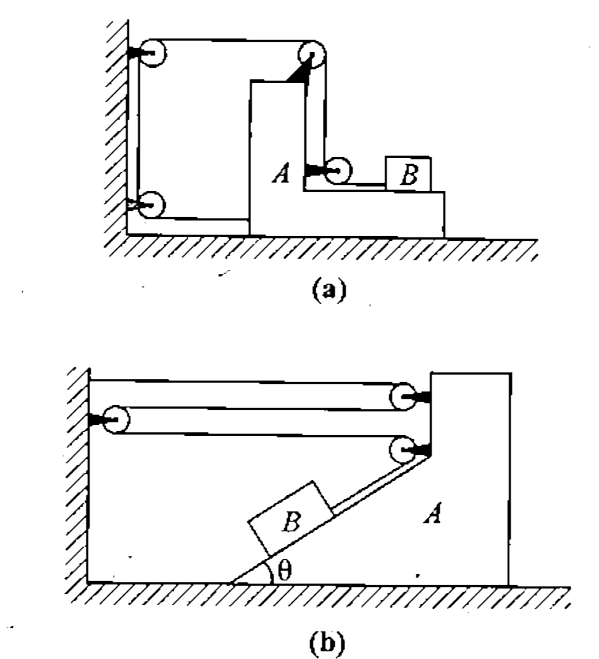
View SolutionIf the point P on string shown in figure-1.96 is pulled down with a velocity v, find the velocity of the block A connected to another string passing over a step pulley with radii ratio `1:2`.
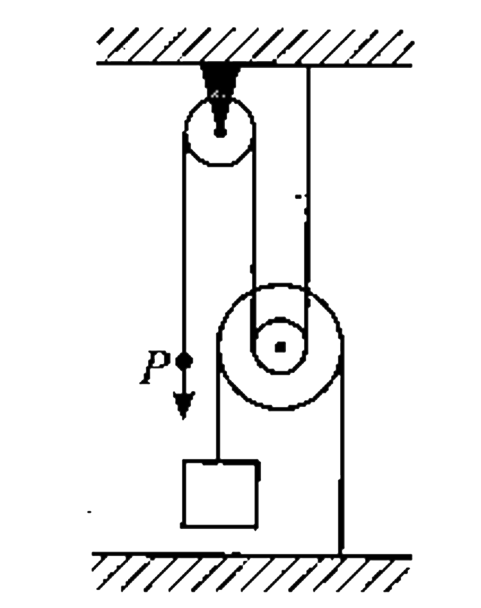
View SolutionFind the constrained relation among the acceleration of blocks A, B and C for the situation shown in figure-1.97. Ratio of radii of step pulley is given as `1:2`.
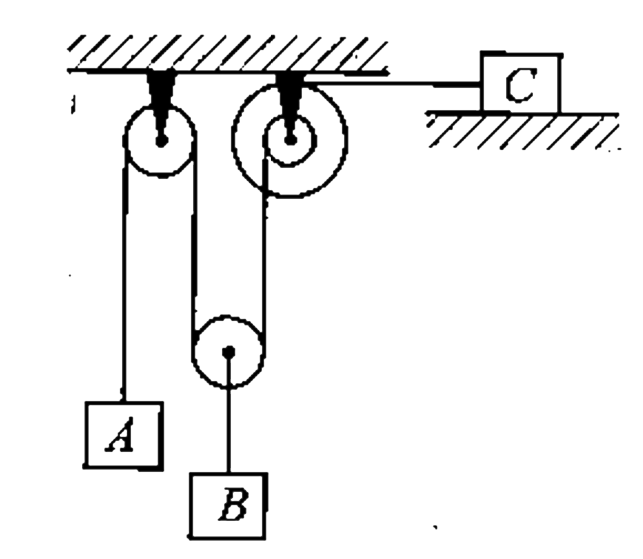
View Solution
Practice Exercise questions and complete solutions for chapter KINEMATICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11