Complete Solutions to Numerical of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| PHYSICS GALAXY | Numerical |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A particle starts moving in +ve x direction with initial velocity of `10 ms^(-1)` with a uniform acceleration of magnitude `2 ms^(-2)` but directed in -ve x direction. What is the distance traversed by the particle in 12 seconds:
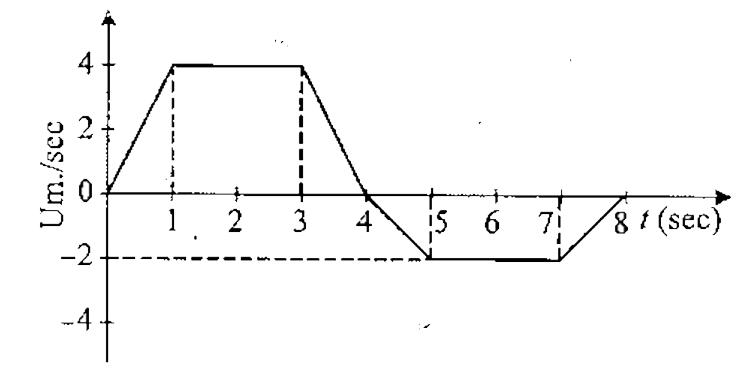
View SolutionFor the velocity time graph shown in Fig. 2 (CF).14, the distance covered by the body in last two seconds of its what fraction if the total distance covered by it in all the seven seconds?
 .
.
View SolutionA particle is moving in a straight line and passes through a point O with a velocity of `6ms^(-1)` The particle moves with a constant retardation of `2ms^(-2)` for 4 s and there after moves with constant velocity. How long after leaving O does the particle return to O
View SolutionThe velocity ofacar travelling on a straight road is given by the equation `v=6+8t-t^(2)` where vis in meters per second and t in seconds. The instantaneous acceleration when `t=4.5 s` is :
View SolutionThe following figure-1.114 shows the linear motion velocity-time graph of a body.The body will be displaced in 5 seconds by:
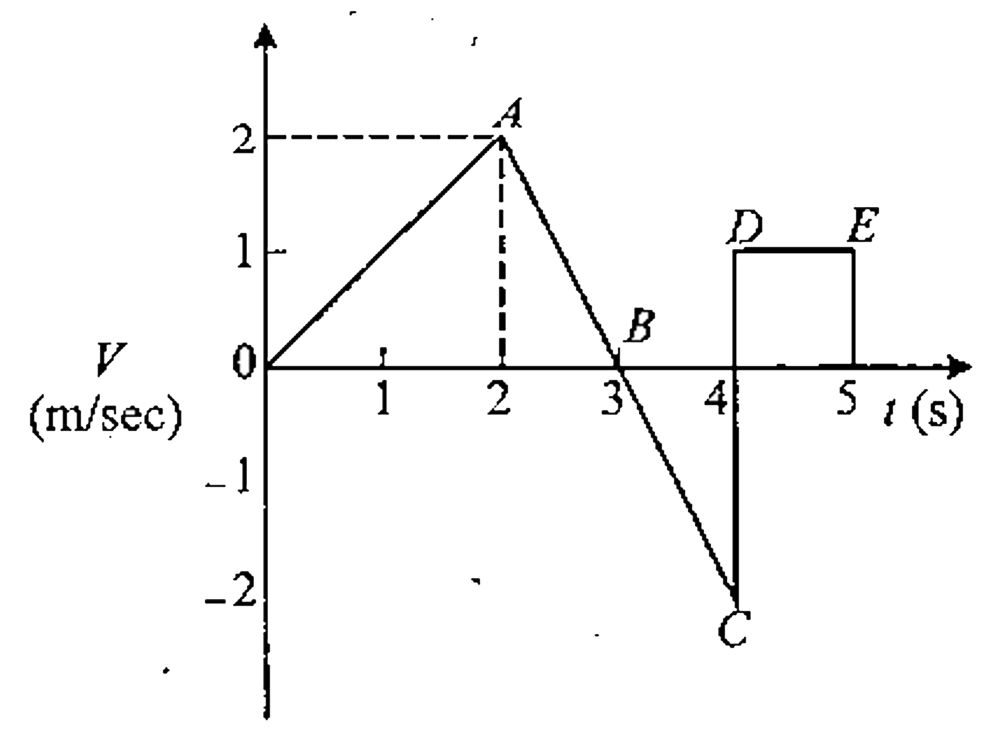
View SolutionIn the above question, the acceleration in the portion OA of the curve will be :
View SolutionIn the above question, which portion of the will have zero acceleration:
View SolutionA particle has initial velocity of `17 ms^(-1)` towards east and constant acceleration of `2 ms^(-2)` due west. The distance covered by it in 9th second of motion is :
View SolutionA ball is thrown vertically upwards from the ground. It crosses a point at the height of 25 m twice at an interval of 4 secs. The ball was thrown with the velocity of
View SolutionThe velocity of a particle moving on the `x-` axis is gienv by `v=x^(2)+x(` for `xgt0)` where `v` is in `m//s` and `x` is in `m`. Find its acceleration in `m//s^(2)` when passing through the point `x=2m`
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
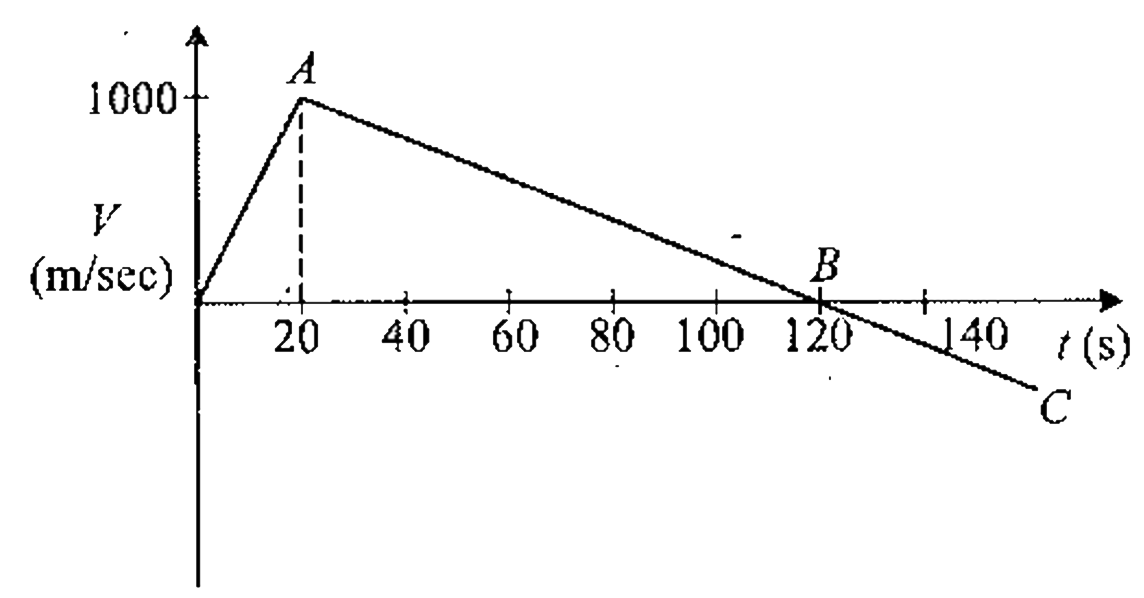
View SolutionIn the previous question, the height attained by the rocket before deceleration is :
View SolutionIn the previous question, the mean velocity of the rocket reaching the maximum height is :
View SolutionIn the above question, the acceleration of the rocket is :
View SolutionThe engine of a motoecycle can produce a maximum acceleration of `5 m//s^(2)`. Its brakes can produce a maximum retardation of `10 m//s^(2)`. What is the minimum time in which the motorcycle can cover a distance of `1.5 km`?
View SolutionTwo balls are dropped from the same point after an interval of 1s. If acceleration due to gravity is `10 m//s^(2)`, what will be their separation 3 seconds after the release of first ball?
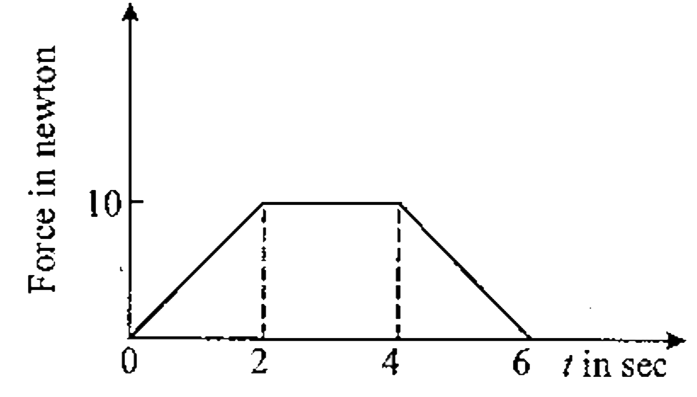
View SolutionThe following figure-1.116 shows the time and applied force graph for a body. What will be the momentum gained by the body in 6 seconds :
View SolutionA person throws balls into the air one after the other at an interval ofone second. The next ball is thrown when the velocityof the ball thrown earlier is zero. To what height the ball rise:
View SolutionA body starts from rest and moves for n seconds with uniform acceleration a, its velocity after n seconds is v. The displacement of the body in last 3 seconds is :
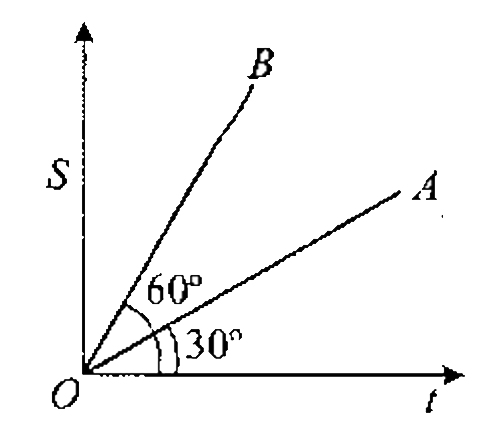
View SolutionThe displacement-time graph for two particle A and B straight lines inclined at angle of `30^(@)` and `90^(@)` with the time axis. The ratio of the velocities `V_(A)` and `V_(B)` is :
View SolutionA particle has an initial velocity of `9m//s` due east and a constant acceleration of `2m//s^(2)` due west. The distance coverd by the particle in the fifth second of its motion is :
View SolutionThe velocity-time graph of a linear motion is shown below. The distance from the origin after 8 seconds is :
View SolutionWater drops fall at regular intervals from a roof. At an instant when a drop is about to leave the roof, the separations between 3 successive drops below the roof are in the ratio
View SolutionA body is in straight line motion with an acceleration given by `a=32-4v`. The initial conditions are at `t=0, v=4`. Find the velocity when `t=ln 2`:
View SolutionA particle is moving in a circle of radius `r` with speed `v` as shown in the figure. The magnitude of change in velocity in moving from `P` to `Q` is

View SolutionA car accelerates from rest at constant rate for the first 10 s and covers a distance x. It covers a distance y in the next 10 s at the same acceleration. Which of the following is true?
View SolutionA particle starts from rest and moves with acceleration a which varies with time `t` as `a=kt` where `k` is a costant. The displacement `s` of the particle at time `t` is
View SolutionThe following shows the time-velocity graph for a moving object. The maximum acceleration will be:
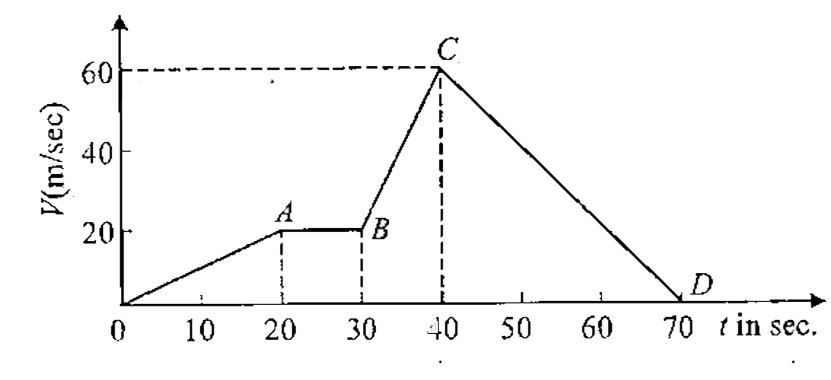
View SolutionIn the above question the magnitude of retardation will be:
View SolutionA rocket is fired vertically upwards and moves with net acceleration of `10 m//s^(2)`. After 1 min the fuel is exhausted. The time taken by it to reach the highest point after the fuel is exhausted will be:
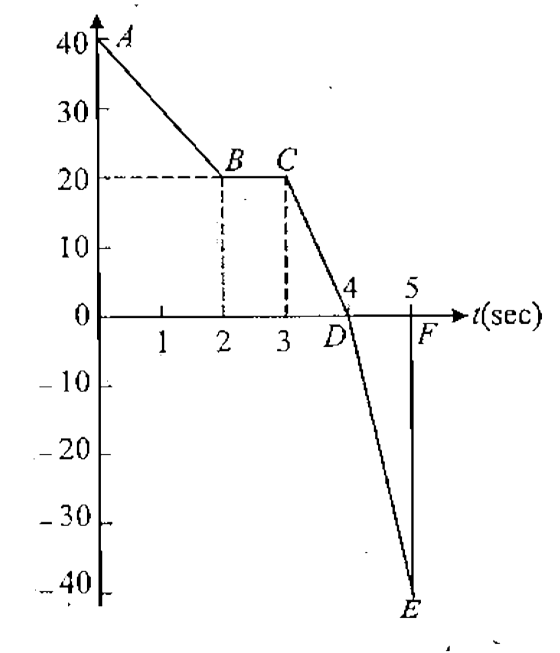
View SolutionIn the following velocity-time graph of a body, the distance and displacement travelled by the body in 5 seconds in meters will be:
View SolutionThe displacement `x` of a body varies with time `t` as `x= -2/3 t^(2)+16 t+2`. The body will come to rest after :
View SolutionA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation `x = (2-5t +6t^(2))m`. The initial velocity of the particle is
View SolutionA parachutist drops first freely from a plane for `10 s` and then his parachute opens out. Now he descends with a net retardation of `2.5 ms^(-2)` If he bail out of the plane at a height of `2495 m` and `g=10 ms^(-2)`, his velocity on reaching the ground will be`.
View SolutionThe acceleration of a'particle starting from rest, varies with time according to the relation `a=kt+c`. The velocity of the particle after time `t` will be :
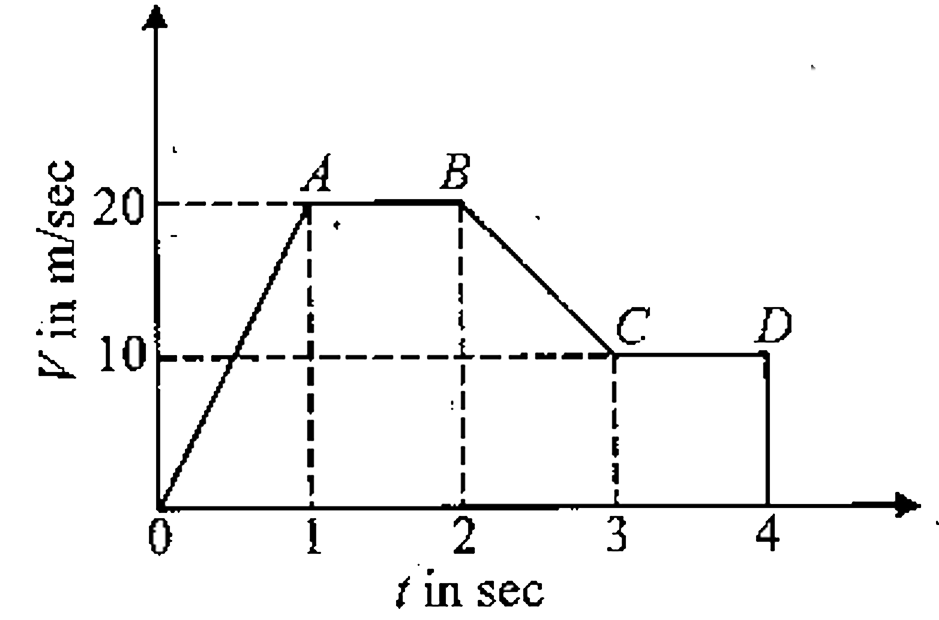
View SolutionThe variation ofvelocity ofa particle moving along a straight line is illustrated in the following figure-1.122. The distance covered by the particle in 4 seconds is :
View SolutionA street car moves rectilinearly from station A to the next station B with an acceleration varying according to the law `f=a-bx`, where a and b are constants and x is the distance from station A. The distance between the two stations & the maximum velocity are :
View SolutionWhen the speed of the car is v, the minimum distance over which it can be stopped is x. If the speed becomes nv, what will be the minimum distance over which it can be stopped during same time:
View SolutionThe following figure-l .123 shows the velocity-time graph of a moving body along a straight line. The displacement and distance travelled in six seconds be respectively given as :
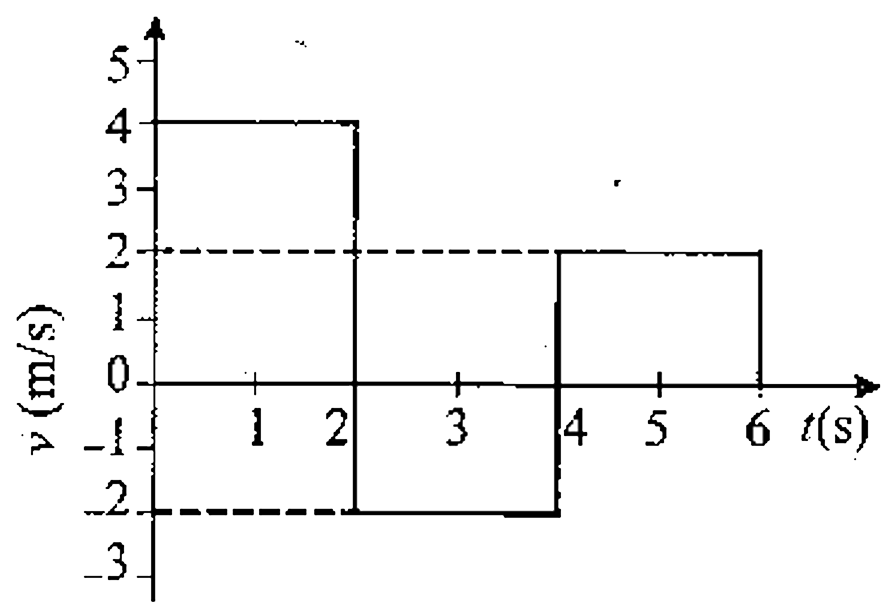
View SolutionA particle is moving in a straight line with initial velocity `u` and uniform acceleration `f`. If the sum of the distances travelled in `t^(th) and (t + 1)^(th)` seconds is `100 cm`, then its velocity after `t` seconds, in `cm//s`, is.
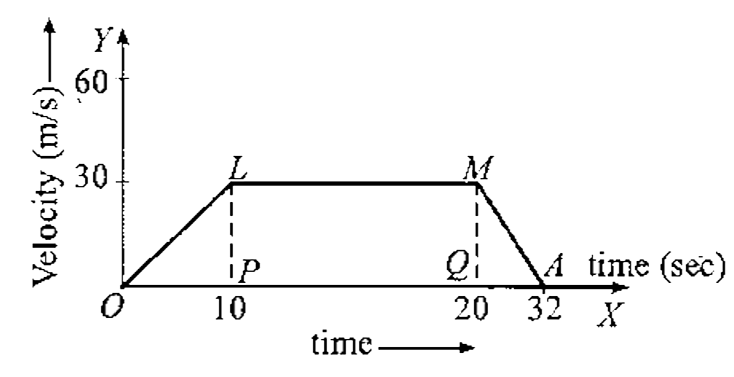
View SolutionThe following figure-1.124 shows the velocity-time graph of a train. The total distance travelled by the train is :
View SolutionA stone falls freely rest. The distance covered by it in the last second is equal to the distance covered by it in the first 2 s. The time taken by the stone to reach the ground is
View SolutionThe figure-1.125 shows the acceleration versus time graph of a train. If it starts from rest, the distance it travels before it comes to rest is :

View SolutionA particle moving on a straight line ultimately comes to rest ? What is the angle between its initial velocity and acceleration ?
View SolutionOna twolaneroada carAistravelling witha speedof `v=5 ms^(-1)`. Two car B and C approach car A in opposite direction with a speed `u=10 ms^(-1)` each. At a certain instant when the B and C are equidistant from A each being `l=1500 m`, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident with C:

View SolutionTwo cars get closer by 8 m every second while traveling in the opposite directions. They get closer by 0.8 m while traveling in the same directions. What are the speeds of the two cars ?
View SolutionAt rain 200m long moving at constant acceleration crosses a bridge 300 m long. It enters the bridge with a speed of 3m/s and leaves it with a speed of 5m/s. What is the time taken to cross the bridge ?
View SolutionA ball is dropped from top of a tower of 100 m height. Simultaneously another ball was thrown upward from bottom of the tower with a speed of `50 m//s (g = 10m//s^(2))`. They will cross each other after
View SolutionA truck travelling due north at 20 m/s turns east and travels at the same speed. What is the change in velocity :
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its position coordinates s from 50m/s to a value approaching zero at = 100 m, the time it takes to reach the 100 m position will be:
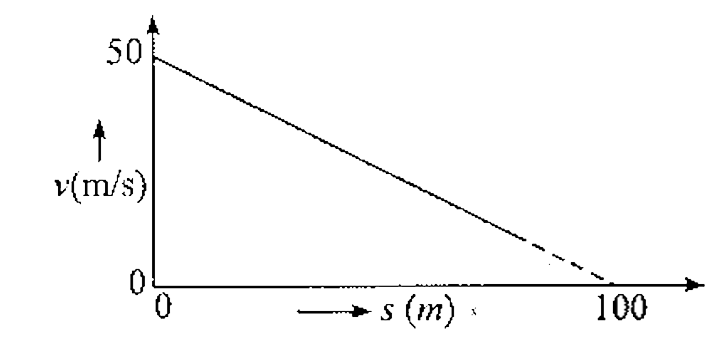
View SolutionA particle moves towards east with velocity `5m//s`. After `10 seconds` its direction changes towards north with same Velocity. The average acceleration of the particle is
View SolutionA body of mass 2kg is moving along north-east direction with a speed `sqrt(2)` m/s. A force of `0.2 N` is applied on the body due west for 10 sec. The final velocity ofthe body is :
View SolutionA person moves 30m north and then 20 m towards east and finally `30sqrt(2)`m in south-west direction. The displacement of the person from the origin will be
View SolutionA river is flowing with a speed of `1 km h^-1` A swimmer wants to go point `C` starting from `A`. He swims with a speed of `5 km h^-1` at an angle `theta` w.r.t. the river flow. If `AB = BC = 400 m`, at what angle with the river bank should the swimmer swim ?
 .
.
View SolutionA blind person after walking each 10 steps in one direction, each of length 80 cm, turns randomly the left or to right by `90^@`. After walking a total of 40 steps the maximum possible displacement the person from his starting position could be (A) 320 m (B) 32 m (C) `16/sqrt2` m (D) `16sqrt2` m
View SolutionA person standing on the roof of a house of height h throws a particle vertically downwards and otherparticle in a horizontal direction with the same speed u. The ratio ofspeeds of the particles on reaching the earth is :
View SolutionA particle moves along a horizontal straight line with a velocity-time relationship as shown in the figure-1.129. The total distance moved by the particle is :
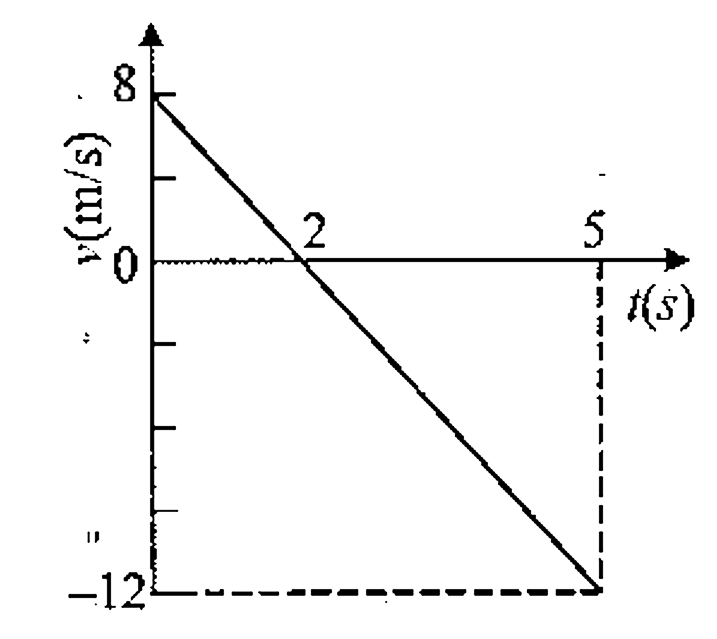
View SolutionA car is going east wards with a velocity of 8m/s. To the passengers in the car, a train appears to be moving north wards with a velocity of 15 m/s. What is the actual velocity of the train:
View SolutionRain is falling vertically with a velocity of 3`kmh^-1`. A man walks in the rain with a velocity of 4`kmh^-1`. The rain drops will fall on the man with a velocity of
View SolutionA man walks in rain with a velocity of 5 kmph. The rain drops strike at him at an angle of `45^(@)` with the horizontal. The downward velocity of the rain drops will be :
View SolutionThe velocities of A and B are marked in the figure-1.130. The velocity of block C is (assume that the pulleys are ideal and string inextensible) :

View SolutionIf `theta` is the angle between the velocity and acceleration of a projectile at a point of its path, its value when the projectile is at the highest point is :
View SolutionIf the angle of projection `theta` corresponds to horizontal range being equal to the maximum height then `tantheta` equals :
View SolutionA thief is running away on a straight road in a jeep moving with a speed of 9m/s. A police man chases him on a motor cycle moving at a speed of 10 m/s. If the instantaneous separation of the jeep from the motorcycle is 100m, how long will it take for the police man to catch the thief?
View SolutionTwo cars are moving in the same direction with the same speed `30 km//hr`. They are separated by a distance of `5 km`, the speed of a car moving in the opposite direction of it meets these two cars at an interval of `4` minutes, will be.
View SolutionA particle is projected upwards with a velocity of 110m/sec at an angle of `60^(@)` with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g `=10m//sec^(2)`
View SolutionThe horizontal range of a projectile is R and the maximum height at tained by it is H. A strong windnow begins to blow in the direction of the motion of the projectile, giving it a constant horizontal acceleration = g/2. Under the same conditions of projection, the horizontal range of the projectile will now be:
View SolutionTwo particles, one with constant velocity 50 m/s and the other with uniform acceleration `10 m//s^(2)` start moving simultaneously from the same place in the same direction. They will be at a distance of 125m from each other after:
View SolutionA stone is dropped from an aeroplane which is rising with acceleration `5 ms^(-2)`. If the acceleration of the stone relative to the aeroplane be `f`, then the following is (are) true :
View SolutionA ball is thrown vertically upwards in air. If the air resistance can not be neglected (Assume it be directly proportionalto velocity) thenthe acceleration of the ball at the highest point will be :
View SolutionIf `y=x-x^(2)` is the of the path of a projectile, then which of the following is incorrect:
View SolutionA rocket is fired upwards. Its velocity versus time graph is shown in the figure-1.131. The maximum height reached by the rocket is:
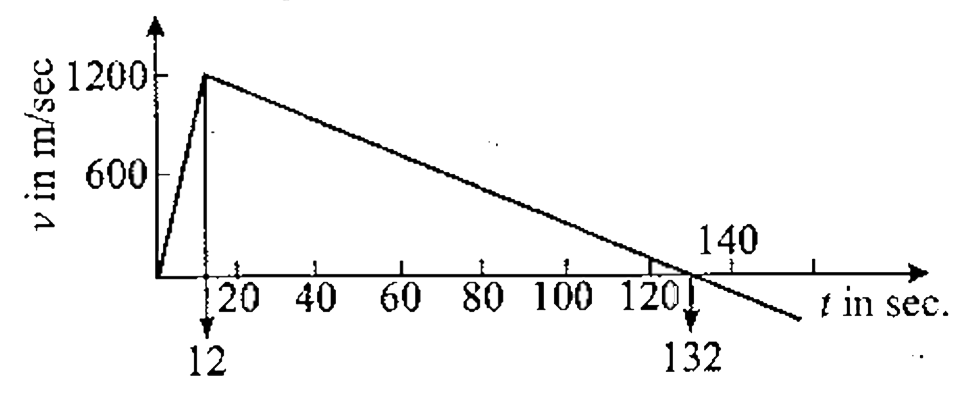
View SolutionA person walks up a stalled escalator in 90 s. When standingon the same escalator, now moving, he is carried in 60 s.The time it would take him to walk up the moving escalator will be:
View SolutionAn object is thrown horizontally from a tower H meter high with a velocity of `sqrt(2gH)` m/s. Its velocity on striking the ground will be :
View SolutionFor a train that travels from one station to another at a uniform speed of `40 kmh^(-1)` and returns to initial station at speed of `60kmh^(-1)` then its average speed is
View SolutionA motor car is going due north at a speed of 50 km/h.It makes a `90^(@)` left turn without changing the speed. The change in the velocity of the car is about :
View SolutionA bird flies for 4 sec with a velocity of `|t-2|` m/s in a straight line, where `t=` time in seconds. It covers a distance of :
View SolutionThree particles A, B and C are thrown from the top of a tower with the same speed. A is thrown up, B is thrown down and C is horizontally. They hit the ground with speeds `v_(A),v_(B) and v_(C)` respectively then,
View SolutionA particle is thrown with a speed u at an angle ` theta` with the horizontal. When the particle makes an angle `phi` with the horizontal. Its speed changes to v :
View SolutionTwo projectiles A and B are projected with angle of projecton `15^(@)` for the projectile A and `45^(@)` for the projectile B. If `R_(A)` and `R_(B)` be the horizontal range for the two projectiles then :
View SolutionIn the arrangement shown in the figure -1.132 if `v_(1)` and `v_(2)` are instaneous velocities of masses `m_(1)` and `m_(2)` respectively, and angle `ACB=2 theta` at the instant then :
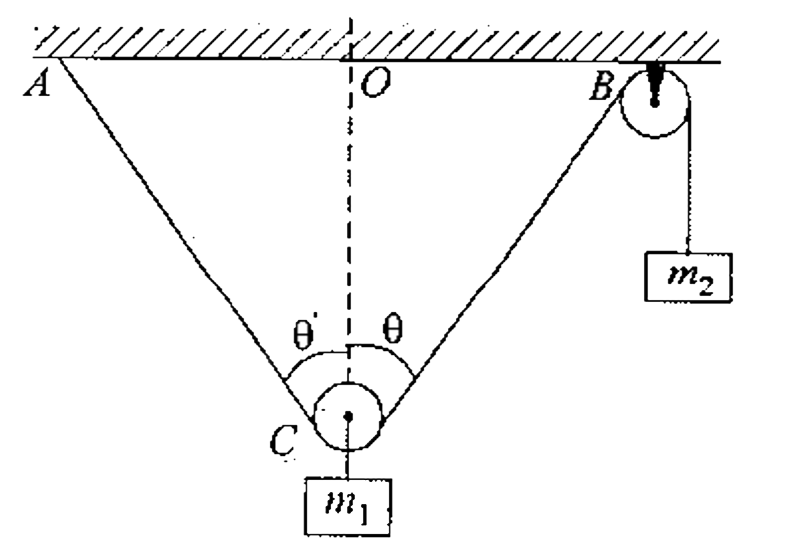
View SolutionA man rows a boat with a speed of 18 km/hr in northwest direction. The shoeline makes an angle of `15^(@)` south of west. Obtain the component of the velocity of the boat along the shoreline:
View SolutionA bullet is fired from a gun falls at a distance half of its maximum range. The angle of projection of the bullet can be :
View SolutionA bus begins to move with an accelaration of ` 1 ms^(-1)` . A man who is `48m` behind the bus starts running at ` 10 ms^(-1)` to catch the bus, the man will be able to catch the bus after .
View SolutionAn experiment on the take-off performance of an aeroplane shows that the acceleration varies as shown in the figure-l. 133, and that it takes 12s to take off from a rest position. The distance along the run way covered by the aeroplane is :
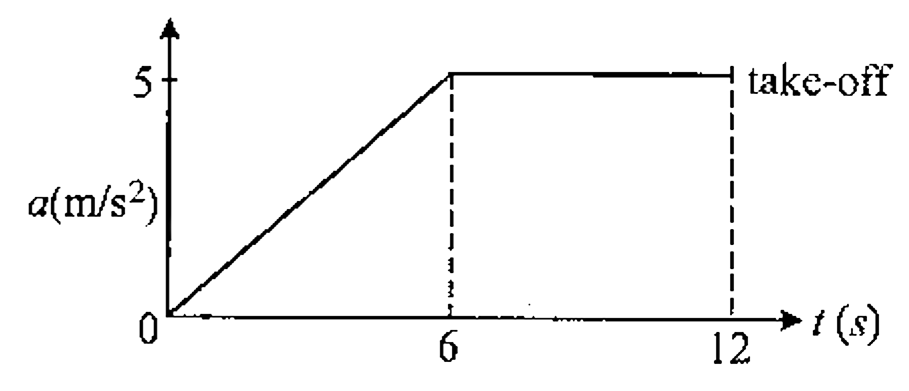
View SolutionWind is blowing in the north direction at speed of 2 m/s which causes the rain to fall at some angle with the vertical. With what velocity should acyclist drive so that the rain appears vertical to him:
View SolutionA particle has a velocity u towards east at `t=0`. Its acceleration is towards west and is constant. Let `x_A` and `x_B` be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA particle thrown up vertically reaches its highest point in time `t_(1)` and returns to the ground in a further time `t_(2)`. The air resistance exerts a constant force on the particle opposite to its direction of motion.
View SolutionThree particles starts from origin at the same time with a velocity `2 ms^-1` along positive x-axis, the second with a velocity `6 ms^-1` along negative y-axis, Find the velocity of the third particle along `x = y` line so that the three particles may always lie in a straight line.
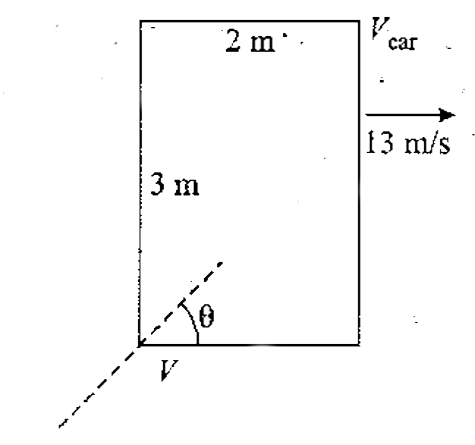
View SolutionA car 2 m long and 3 m wide is moving at 13m/sec when a bullet hits it in a direction making an angle `theta=tan^(-1) 3//4` with the car as seen from the street. The bullet enters one edge of the comer and passes out at the diagonally opposite comer. Neglectingany interaction between bullet and car find the time for the bullet to cross the car :
View SolutionRain is falling with a speed of 4nVs inadirection making an angle of `30^(@)` with vertical towards south. What should be the magnitude & direction of velocity of cyclist to hold his umbrella exactly vertical, so that rain does not wet him:
View SolutionThe greatest acceleration or deceleration that a train may have is a. The minimum time in which the train may reach form one station to the other seprated by a distance is-
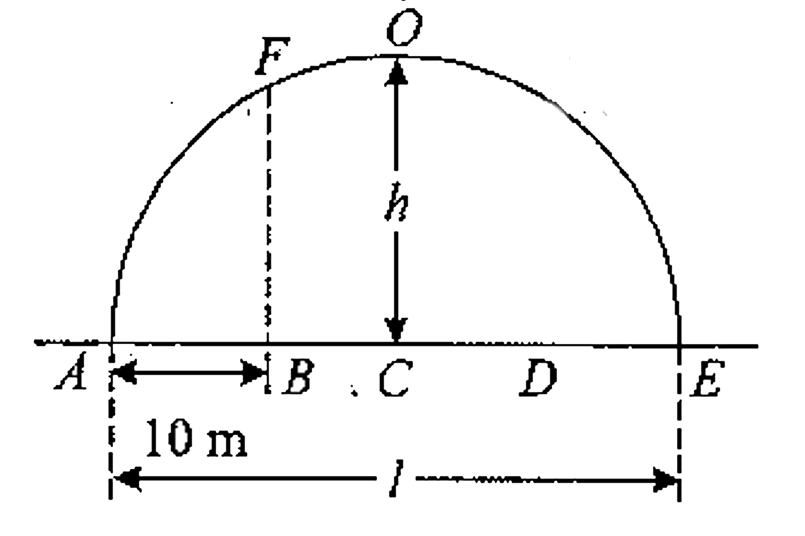
View SolutionA car of mass `=m=1000 kg` is moving with constant speed `v=100 m//s` on a parabolic shaped bridge AFOE of span force applied by the bridge on the car when he car is at point E, is:
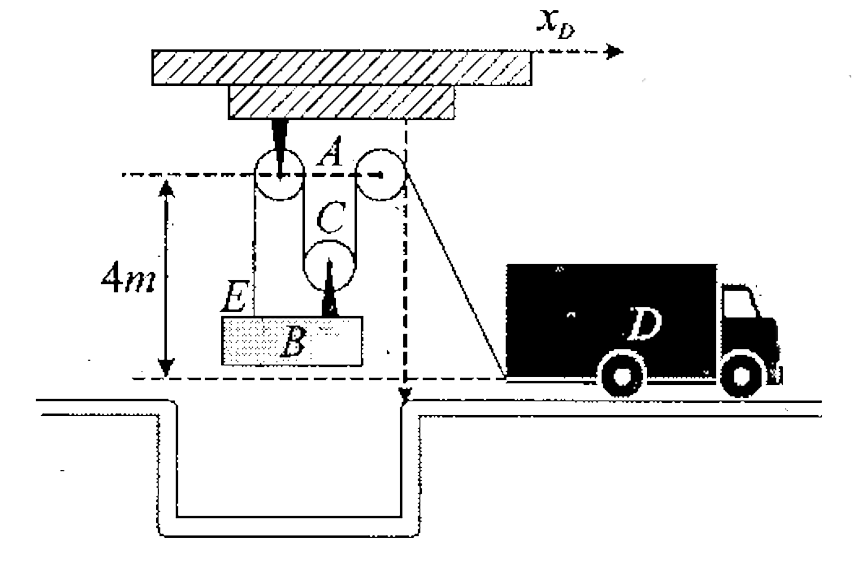
View SolutionA block B is suspended from a cable that is attached to the block at E, wraps around three pulleys and is tied to the back of a truck D. Ifthe tmck starts from rest when `x_(D)` is zero and moves forward with a constant acceleration of `a_(P)=3//2 m//s^(2)`, if the speed of the block at the instant `x_(D)=3 m` is :
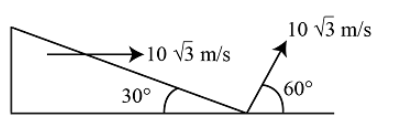
View SolutionA particle is projected at an angle `60^@` with speed `10(sqrt3)m//s`, from the point A, as shown in the figure. At the same time the wedge is made to move with speed `10 (sqrt3) m//s` towards right as shown in the figure. Then the time after which particle will strike with wedge is
View SolutionAn aeroplane flies along a straight line from `A` to `B` with a speed `v_(0)` and back again. A steady wind `v` is blowing if `AB=l` then
a)total time for the trip is `(2v_(0)l)/(v_(0)^(2)-v^(2))` if wind blows along the line `AB`
b)total time for the trip is `2l/sqrt(v_(0)^(2)-v^(2))`,if wind blows perpendicular to the line `AB`
c)total time for the trip decrease because of the presence of wind
d)total time for the trip increase because of the presence of wind
View SolutionIn the arrangement of rigid links of equal length `l`, they can freely rotate about the joined ends as shown in the figure- 1.138. If the end U is pulled horizontally with constant speed 20 m/s, find the approx. speed of end `P` when the angle SUT is `90^(@)`.

View SolutionA snapshot of apetrol engine is given in which piston is moving downwards with velocity `40sqrt(3)` m/s. Find the angular velocity of the shaft:
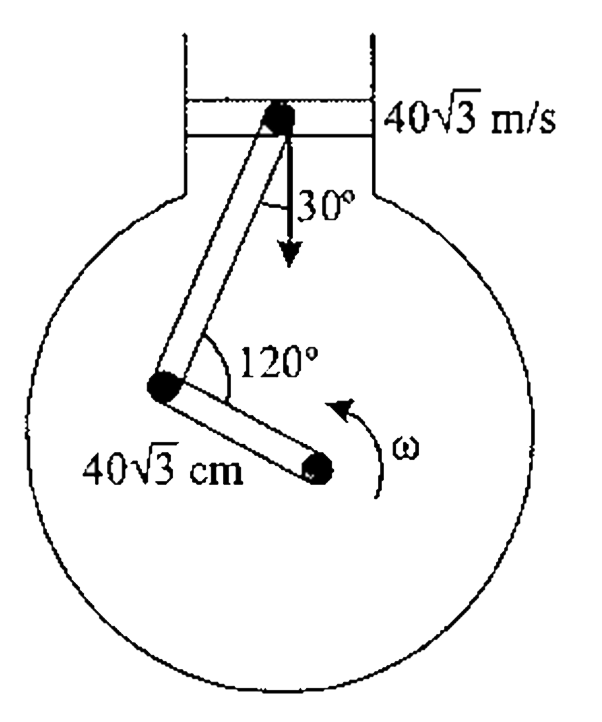
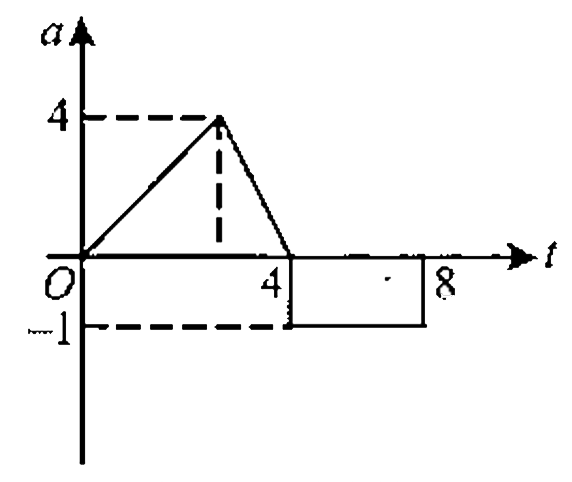
View SolutionThe acceleration time graph of a particle is shown in the figure-1.140. What is the velocity of particle at t=8s, if initial velocity of particle is 3 m/s? (Assume motion is 1 dimension) :
View SolutionA particle is moving on a circular path of radius R with uniform angular speed `omega`. The magnitude of average velocityof particle during time `t=0` to `t=(2pi)/(3 omega)`:
View Solution
Numerical questions and complete solutions for chapter KINEMATICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11