Complete Solutions to Practice Exercise of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| PHYSICS GALAXY | Practice Exercise |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
A factory worker pushes a 25.0 kg crate downward at an angle of `30^(@)` below the horizontal a distance of 6.0 m along a level floor.
(a) What magnitude of force must the worker apply to move the crate at constant velocity, if the coefficient of kinetic friction between the crate and floor is 0.3 ?
(b) How much work is done on the crate by this force when the crate is pushed a distance of 6.0 m?
(c) How much work is done on the crate by friction during this displacement ?
(d) How much work is done by the normal force and by gracity ?
(e) What is the total work done on the crate ? Take `g=10m//s^(2)`
View SolutionFind the work a boy of weight 55 kg has to do against gravity when climbing from the bottom to the top of a 3.0 m high tree.
View SolutionA force of 20.0 N is required to hold a spring stretched by 5.0 cm from its equilibrium position. How much work was done in stretching the spring ?
View SolutionA spring requires 46 J of work to extend it 12 cm and 270 J of work to extend it 27 cm. Is the spring force linearly varying with the stretch.
View SolutionA force is given by `F=kx^(2)` where x is in meters and `k=10 N//m^(2)` What is the work done by this force when it acts from x=0 to x=0.1m ?
View SolutionA block shown in figure -3.12 slides on a semicircular frictionless track. If it starts from rest at position A, what is its speed at the point marked B ? Take `g=10m//s^(2)`
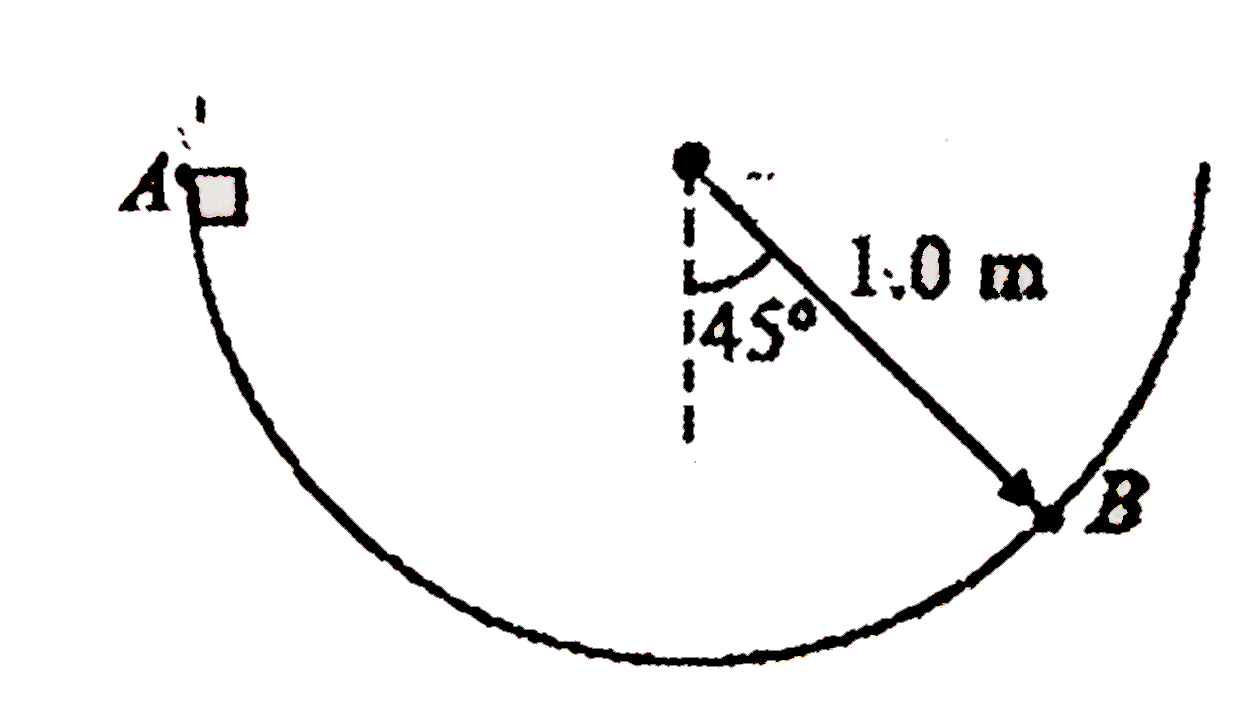
View SolutionA stone is dropped by an astronaut from a height of 1.47 m above the surface of a planet. When stone reaches a point P at a height of 0.32 m it attains a speed of `4.1 m//s` Is the planet earth ?
View SolutionA brick is placed on a vertical compressed massless spring of force constant `350N//m` attached to the ground. When the spring is released the brick is propelled upward. If the brick mass is 1.8 kg and will reach a maximum height of 3.6 m above its initial position on the compressed spring, what distance must the spring be compressed initially ? Take `g=10m//s^(2)`
View SolutionIn figure-3.13, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless until the block reaches the higher level. There a frictional force stops the block in a distance d. The block's initial speed `v_(0)` is `6 m//s` the height difference h is 1.1 m and the coefficient of kinetic friction `mu` is 0.6 find d. Take `g=10m//s^(2)`

View SolutionA particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length `l=3m`. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is `mu_k=0.2`. The particle is released at point A which is at height `h=1.5m` above the flat part of the track. Where does the particle finally come to rest?

View SolutionA 80 kg person expends 400 W when walking on a horizontal tracker belt at a speed of 7.2 kph. When the tracker belt is inclined without changing the speed, the person's expended power increases to 600 W. Estimate the angle of incline of the tracker belt by assuming that all of the increased output power goes into overcoming the force of gravity. Assume constant friction by tracker belt in both horizontal and inclined position `Take g=10m//s^(2)`
View SolutionA bus of mass 1000 kg has an engine which produces a constant power of 50 kW. If the resistance to motion, assumed constant is 1000 N. The maximum speed at which the bus can travel on level road and the acceleration when it is travelling at 25 m/s, will respectively be -
View SolutionAn automobile engine develops 30 hp in moving the automobile at a constant speed of 50 `miles//hr` What is the average retarding force due to such things as wind resistance, internal friction, tire friction, etc. ?
View SolutionThe force needed to pull the tape through an audio cassette player is 0.98 N. In operation the tape travels at a constant speed of 2.5 `cm//s` The motor consumes a power of 1.8 W. what percentage of the power input to the motor is required to pull the tape at its operating speed ?
View SolutionThe power P delivered by a windmill whose blades sweep in a circle of diameter D by a wind of speed v is proportional to the square of the diameter and the cube of the wind speed. Show that this dependence on diameter and wind speed exist when 100% energy transfer takes place. Also show that
`P=pi/8 rhoD^(2)v^(3)`
Where is `rho` the density of air.
View SolutionA train of mass `10^(6)` kg is going up an incline plane with incline 1 in 49 at a rate of `10m//s` if the resistance due to friction be 10 N per metric ton, calculate the power of the engine. If the engine is shut off, how far will the train move before it comes to rest ? take `g=9.8m//s^(2)`
View SolutionA car is moving with speed `30m//sec` on a circular path of radius 500 m . Its speed is increasing at the rate of , `2m//sec^(2)`, What is the acceleration of the car
View SolutionA solid body starts rotating about a stationary axis with an angular acceleration `beta` = at. How soon after the beginning of rotation will the total acceleration vector of a general point on the body form an angle `alpha` with its velocity vector ?
View SolutionA solid body rotates with deceleration about a stationary axis with an angular deceleration `betapropsqrt(omega)`, where `omega` is its angular velocity. Find the mean angular velocity of the body averaged over the whole time of rotation if at the initial moment of time its angular velocity was equal to `omega_0`.
View SolutionA solid body starts rotating about a stationary axis with an angular acceleration `alpha=alpha_(0) cos theta`, where `alpha_(0)` is a constant and `theta` is an angle of rotation from the initial position. Find the angular velocity of the body as a function of `theta`.
View SolutionA ball is attached to a horizontal cord of length `l` whose other end is fixed. (a) If the ball is released, what will be its speed at the lowest point of its path? (b) A peg is located a distance `h` directly below the point of attachment of the cord. If `h=0.75l`, what will be the speed of the ball when it reaches the top of its circular path about the peg?
View SolutionAn automatic tumble dryer has a 0.65 m diameter basket that rotates about a horizontal axis. As the basket turns, the clothes fall away from the basket at a point `60^(@)` from the vertical what is the rate of rotation of dryer drum ? Take `g=10 m//s^(2)`
View SolutionA smooth circular tube is held in a vertical position. A small ball which is free to slide inside the tube is held stationary at the highest position in the tube. If the ball is slightly displaced from its position of rest, show that the force exerted by the ball on the wall of the tube is given as `mg(3 costheta-2)` , where m is the mass of the ball and `theta` is the angular displacement from highest position. Upto what value of `theta` , this result will remain valid.
View SolutionA particle is suspended from a fixed point by a string of length 5m. It is projected from the equilibrium position with such a velocity that the string slackens after the particle has reached a height 8 m above the lowest point. Find the velocity of the particle, just before the string slackens. Find also, to what height the particle can rise further Take `g=10 m//s^(2)`
View SolutionA stunt pilot in an airplane diving vertically downward at a speed of 220 kph turns vertically upward by following an approximately semicircular path with a radius of 180 m.
(a) How many g's does the pilot experience due to his motion alone ?
(b) By what factor does the pilot's weight appear to increase at the bottom of the dive ?
View SolutionA particle of mass `m` initially at rest starts moving from point `A` on the surface of a fixed smooth hemisphere of radius `r` as shown. The particle looses its contact with hemisphere at point `B.C` is centre of the hemisphere. The equation relating `theta` and `theta'` is
 .
.
View SolutionA space station 960 m in diameter rotates fast enough that the artificial gravity at the outer edge is 1.5 g
(a) What is the frequency of rotation ?
(b) What is its period ?
(c) At what distance from the center will the artificial gravity be 0.75 g ? Take `g=10m//s^(2)`
View SolutionCalculate the angle of banking required for a curve of 200 m radius so that a car rounding the curve at 80 kph would have no tendency to skid outward or inward. Assume the surface is frictionless. Take `g=10m//s^(2)`
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is ` 0.05 m` and the speed of rotation is `2 rev//s`, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R(figure). The system is set in rotation with a constant angular velocity `omega` about a vertical axis `OO^'`. Find the angle `theta` corresponding to the steady position of the sleeve.
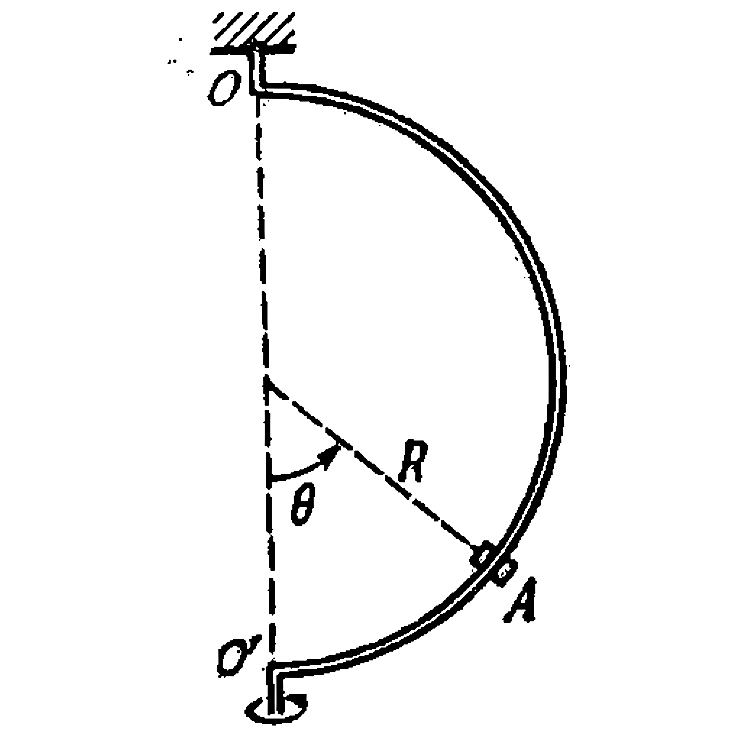
View SolutionA hemispherical bowl of radius `R=0.1m` is rotating about its own axis (which is verticle) with an angular velocity `omega`. A particle of mass `10^(-2)kg` on the smooth inner surface of the bowl is also rotating with the same `omega`. The particle is at a height `h` from the bottom of the bowl (a) obtain the relation betweemn `h` and `omega`. what is the minimum value of `omega` needed, in order to have a non-zero value of `h`? (b) it is desired to measure `g` using this set up, by measuring `h` accurately. assuming that `R` and `Omega` are known precisely and least count in the measurement of `h` is `10^(-4)m`, what is the minimum possible error `Deltag` in the measured value of `g`? `(g=10m//s^(2))`
View SolutionA smooth light horizontal rod AB can rotate about a vertical axis passing through its end A. The rod is fitted with a small slieeve of mass m attached to the end A by a weightless spring of length `l_0` and stiffness `x`. What work must be performed to slowly get this system going and reaching the angular velocity `omega`?
View SolutionAn ideal massless spring `S` can compressed `1.0` m in equilibrium by a force of `100 N`. This same spring is placed at the bottom of a friction less inclined plane which makes an angle `theta =30^@` with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by `2 m. if `g =10 ms^(-2)`, what is the speed of just before it touches the spring?
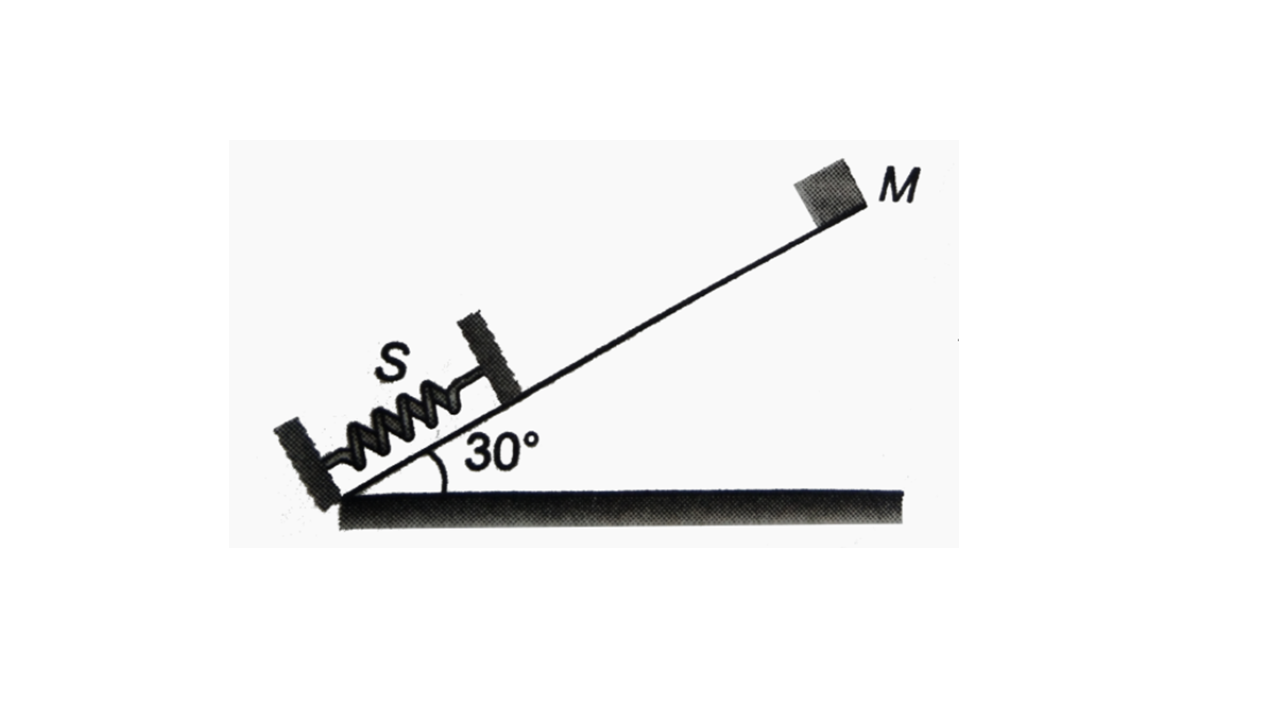 .
.
View SolutionA particle of mass `0.5kg` travels in a straight line with velocity `v=ax^(3//2)` where `a=5m^(-1//2)s^-1`. What is the work done by the net force during its displacement from `x=0` to `x=2m`?
View SolutionA block of mass `m` attached with a massless spring of force constant k The block is placed over a rough inclined surface for which the coefficient of friction is `0.5` the system is released from rest when the spring was unstretched The minimum mass of the hanging block to move the small block "m" up the plane is (neglect mass of spring and pulley and friction in pulley)
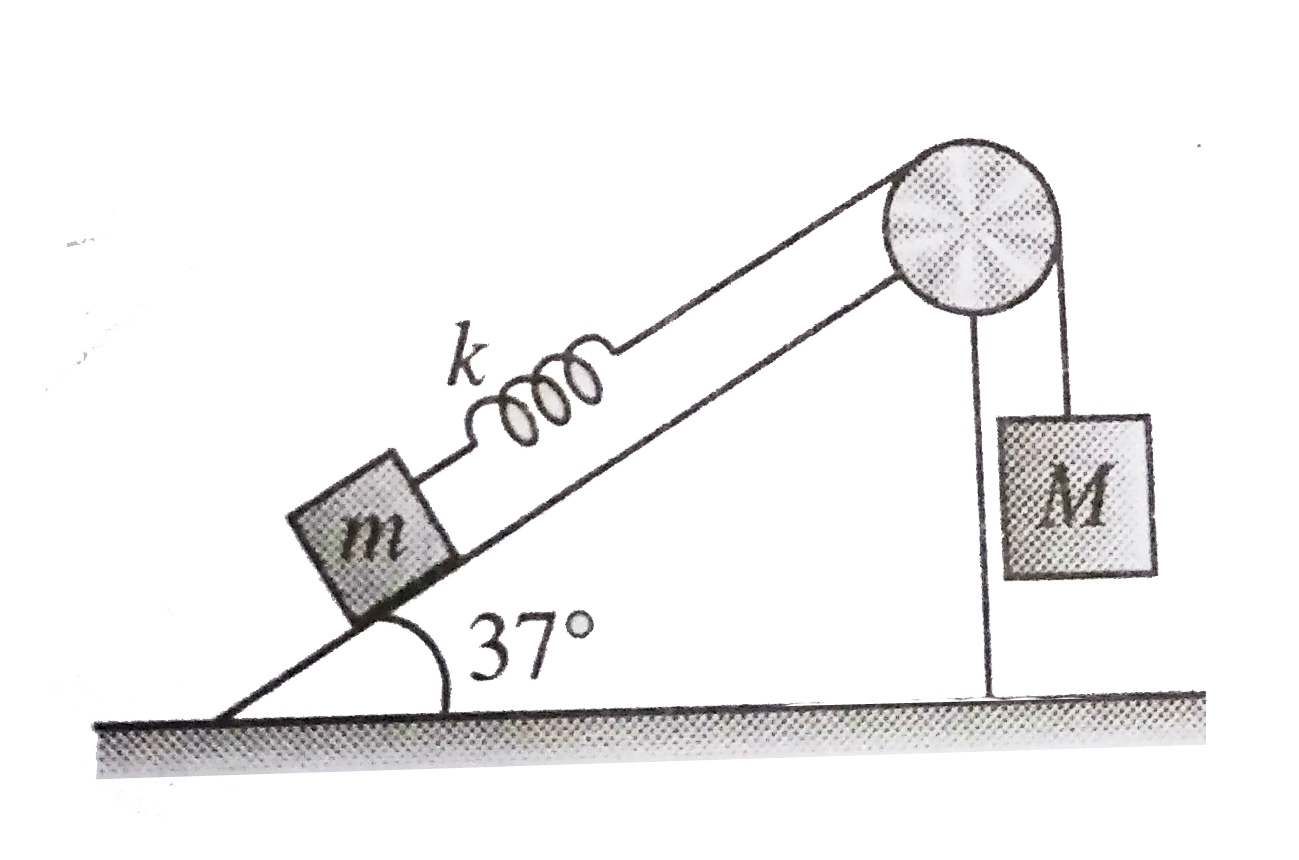
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximate given by `U(r) = (a)/(r^(12)) - (b)/(r^(6))`, where `a` and `b` are constants and `r` is the distance between the atoms. If the dissociation energy of the molecule is `D = [U (r = oo)- U_("at equilibrium")],D` is
View SolutionA bob tied to the end of a string of length 2m, other end of which is fixed at a point in a vertical wall at a point O. The bob is imparted a vertical downward velocity of `5 m//s` when the string is horizontal and swings in a vertical plane. Find the angular displacement of the bob from its initial position, when the string breaks. Given that the tensile strength of the string is twice the weight of the bob. Take `g=10 m//s^(2)`
View SolutionIn a spring gum having spring constant 100 `N//m` a small ball of mass 0.1 kg is put in its barrel by compressing the spring through 0.05 m
(a) Find the velocity of the ball when the spring is released.
(b) Where should a box be placed on the ground so that the ball falls in it, if the ball leaves the gun horizontally at a height of 2m above the ground. Take `g=10 m//s^(2)`
View SolutionA chain AB of length equal to the quarter of a circle of radius R is placed on a smooth hemisphere as shown in figure -3.66. When it is released, it starts falling. Find the velocity of the chain when it falls of the end B from the hemisphere.

View SolutionA particle of mass m approaches a region of force starting from `r=+infty` The potential energy function in terms of distance r from the origin is given by,
`U(r) = K/(2a^(3))(3a^(2)-r^(2)) for 0 lt r lt a`
`=K//r for r gt a`
(a) Derive the force F(r) and determine whether it is repulsive or attractive.
(b) With what velocity should the particle start at `r=infty` to cross over to other side of the origin.
(c) If the velocity of the particle at `r= infty` is `sqrt((2K)/(am))` towards the origin describe the motion.
View SolutionA particle moving in a straight line is acted by a force, which works at a constant rate and changes its velocity from u to v in passing over a distance x. The time taken will be -
View SolutionThe potential energy function of a particle in a region of space is given as `U=(2xy+yz)` J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View Solution
Practice Exercise questions and complete solutions for chapter WORK, ENERGY AND POWER of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11