Complete Solutions to Illustration of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| PHYSICS GALAXY | Illustration |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
A boy pulls a 5 kg block 20 metres along a horizontal sur- face at a constant speed with a force directed 45° above the horizontal. If the coefficient of kinetic friction is 0.20, how much work does the boy do on the block?
View SolutionA body is thrown on a rough surface such that the friction force acting on it is linearly varying with the distance travelled by it as `f=ax+b`. Find the work done by the friction on the box if before coming to rest the box travels a distance s.
View SolutionA force varying with distance is given as `F=ae^(-bx)` acts on a particle of mass m moving in a straight line. Find the work done on the particle in its displacement from origin to a distance d.
View SolutionA 2kg body is displaced on a rough plane with friction coefficinet `mu=0.5` with a variable force `F=(4x^(2)+15)` N. Find the kinetic energy of the block after the block has travelled a distance 5 m.
View SolutionA body of 4 kg mass placed on a smooth horizontal surface experiences a force varying with displacement of block as shown in figure-3.7. Find the speed of the body when force ceases to act on it.

View SolutionA trolley car starts from rest at the top of a hill as shown in figure -3.9 and moves down the curved track. Determine its speed as it reaches the bottom. Assume that the work done by frictional forces is negligible.
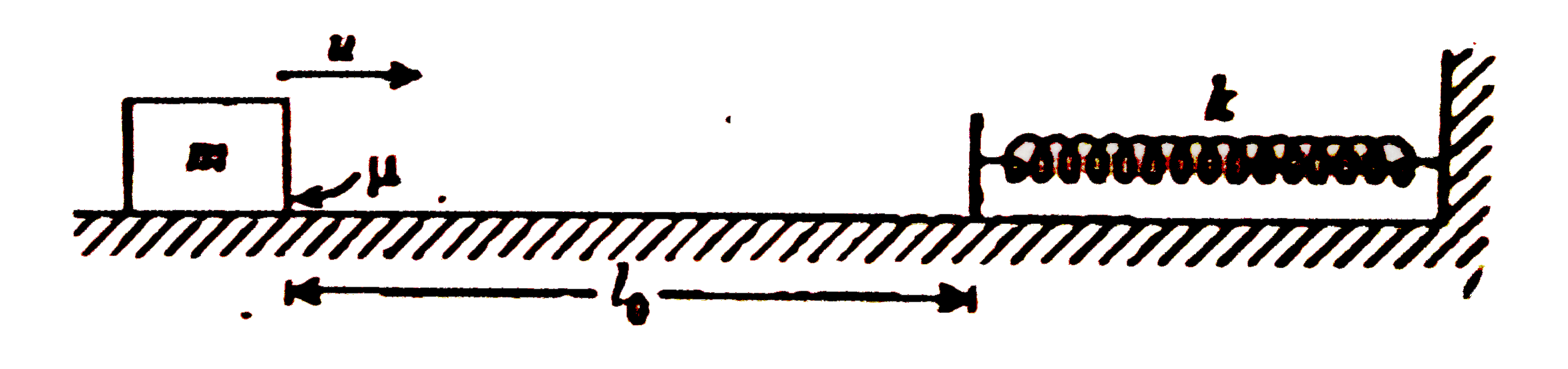
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance `l_(0)` from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is `mu`..
View SolutionFigure. shows a rough incline at an angle `theta` with coefficient of friction `mu` At the bottom a spring is attached with force constant k. A block of mass m is released from a position at a length l away from the spring. Write down the work energy equations to find the maximum compression in the spring and the distance by which the block rebound up the inclined plane. the distance by which the block rebound up the inclined plane

View SolutionA disc of mass `50 g` slides with zero initial velocity down an inclined plane at an angle `30^@` to the horizontal. Having traversed a distance of `50 cm` along the horizontal plane, the disc stops. Find the work performed by the friction forces over the whole distance, assuming the friction coefficient `0.15` for both inclined and horizontal planes. `(g =10 m//s^(2))`.
View SolutionA body of mass `m` is thrown at an angle `alpha` to the horizontal with the initial velocity `v_0`. Find the mean power developed by gravity over the wholetime of motion of the body, and the instantaneous power of gravity as a function of time.
View SolutionAn electric motor that can develop 1.0 hp is used is used to lift a mass of 25 kg through a distance of 10.0 m. What is the minimum time in which it can do this ? (Take `g=10m//s^(2))`
View SolutionA pump is required to lift `1000kg` of water per minute from a well `12m` deep and eject it with a speed of `20ms^-1`. How much work is done per minute in lifting the water and what must be the power output of the pump?
View SolutionA small body of mass m is located on a horizontal plane at the point O. The body of mass m is located on a horizontal plane at the point O. The body acquires a horizontal velocity `v_0`. Find,
(a) the mean power developed by the friction force during the whole time of motion, if the friction coefficient `k=0.27`, `m=1.0kg`, and `v_0=1.5m//s`,
(b) the maximum instantaneous power developed by the friction force, if the friction coefficient varies as `k=alphax`, where `alpha` is a constant, and x is the distance from the point O.
View SolutionA stone with a mass of 0.9 kg is attached to one end of a string 0.8 m long. The string will break if its tension exceeds 500 N. The stone is whirled in a horizontal circle on a frictionless table top. The other end of the string is kept fixed. Find the maximum speed of the stone, it can attain without breaking the string.
View SolutionA person stands on a spring balance at the equator.
(a) How much is the reduction in weight as measured by the balance.
(b) If the speed of earth's rotation is changed such that the balance reading is half of its true weight, what will be the length of the day in this case? `(g=10m//s^(2),R_(e)=6400km)`
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle `theta` with the horizontal, at a point where the velocity of particle makes an angle `theta//2` with the horizontal.
View SolutionA wheel rotates around a stationary axis so that the rotation angle `theta` varies with time as `theta=at^(2)` where `a=0.2rad//s^(2)`. Find the magnitude of net acceleration of the point A at the rim at the moment `t=2.5s` if the linear velocity of the point A at this moment is `v=0.65m//s`.
View SolutionA stone is thrown horizontally with a velocity of `10m//sec`. Find the radius of curvature of it’s trajectory at the end of `3 s` after motion began. `(g=10m//s^(2))`
View SolutionA 40 kg mass, hanging at the end of a rope of length l, oscillates in a vertical plane with an angular amplitude `theta_0.` What is the tension in the rope when it makes en angle `theta` with the vertical ? If the breaking strength of the rope is 80 kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionFigure shows a loopthe loop track of raidus R. A car (without engine) starts from a platform at a distance h above the top of the loop and goes around the loop without falling off the track. Find the minimum value of h for a successful looping. Neglect friction.

View SolutionFigure shows a smooth track, a part of which is a circle of radius `r`. A block of mass `m` is pushed against a spring of spring constant `k` fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force `mg` when it reaches the point P, where the radius of the track is horizontal.

View SolutionA small box of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the box makes an angle of `30^(@)` with the vertical. The box is released from this position
(a) What is the force exerted by the sphere on the box just after the release ?
(b) Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA particle is suspended from a fixed point by a string of lengh `5m`. It is projected from the equilibrium position with such a velocity that the string slakens after the particle has reached a height `8m` above lowest point. Find the velocity of the particle, just before the string slackens.
Find also, to what to what height the particle can rise further?
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA particle of mass m is attached to one end of a weightless and inextensible string of length L. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other and is attached a small particle of equal mass m. The system is set in motion with the first particle describing a circle on the table with constant angular velocity `omega_(1)` and the second particle moving in the horizontal circle as a conical pendulum with constant angular velocity `omega_(2)` Show that the length of the portions of the string on either side of the hole are in the ratio `omega_(2)^(2): omega_(1)^(2)`
View SolutionA particle describes a horizontal circle on the smooth inner surface of a conical funnel as shown in figure - 3.44. If the height of the plane of the circle above the vertex is 9.8 cm, find the speed of the particle.
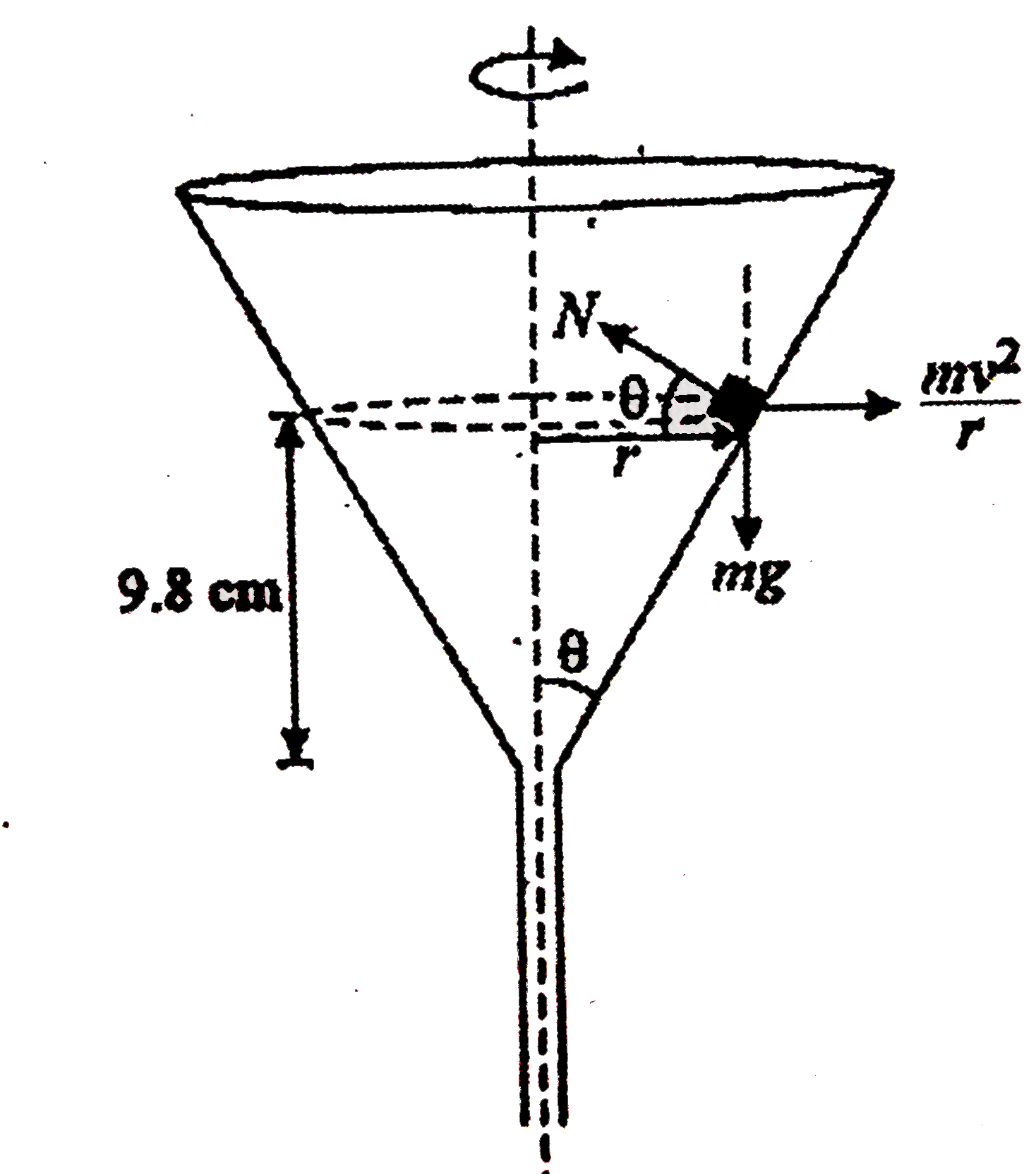
View SolutionA car starts from rest in a circular flat road of radius R with an acceleration a. The friction coefficient between the road and the tyred is `mu` Find the distance car will travel before is start skidding.
View SolutionA particle is attached by means of two equal strings to two points A and B in the same vertical line and describes a horizontal circle with a uniform angular speed. If the angular speed of the particle is `2sqrt(2g//h)` with AB=h, show that the ratio of the tensions of the strings is `5:3`
View SolutionA hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is `theta`, find the angular speed at which the bowl is rotating.
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximately given by `U(x) =a/x^(12)-b/x^(6)` where a and b are constant and x is the distance between the atoms. Find the dissoociation energy of the molecule which is given as `D=[U(x- infty)-U_(at equilibrium)]`
View SolutionFind the expresstion of potential energy `U(x,y,z)` for a conservative force in a force field where force is given as `vec(F)=yzhat(i)+xyhat(k)` Consider the zero of the potential energy chosen at the point (2,2,2).
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by `U(x) =(x^(2)/2-x)` joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionA chain of mass m and radius R placed on a smooth table is revolving with a speed v about a vertical axis coinciding with the symmetry axis of the chain. Find the tension in the chain.
View SolutionFigure-3.54(a) shows a cone of half angle `theta` on which a chain of mass m is resting with sufficient friction so that it will not slip on the surface of cone. If cone starts rotaring at an angular velocity `omega` find the tension developed in the chain.
View SolutionA uniform chain is held on a frictionless table with one third of its length hanging over the edge. IF the chain has a length l and a mass m, how much work is required to pull the hanging part back on the table ?
View SolutionA particle of mass m moves along a circle of radius R with a normal acceleration varying with time as `a_(N)=kt^(2)` where k is a constant. Find the time dependence of power developed by all the forces acting on the particle and the mean value of this power averaged over the first t seconds after the beginning of the motion.
View SolutionA system consists of two identical blocks, each of mass m, linked together by the compressed weightless spring of stiffness k, as shown in figure -3.57. The blocks are connected by a thread which is burned through at a certain moment. Find
(a) At what values of initial compression, the inital compression of the spring, the lower block will bounce up after the thread has been burned through
To what height will the centre of gravity of this system will rise if the initial compression of the spring is 7 `mg//k`

View SolutionA horizontal plane supports a plank with a bar of mass `m=1.0kg` placed on it and attached by a light elastic non-deformed cord of length `l_0=40cm` to a point O(figure). The coefficient of friction between the bar and the plank equals `k=0.20`. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord deviates from the vertical by an angle `theta=30^@`. Find the work that has been performed by that moment by the friction force acting on the bar in the reference frame fixed to the plane.

View SolutionA table with smooth horizontal surface is turning at an angular speed `omega` about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
View SolutionA car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is `mu` Find the speed at which car will skid and also find the distance after travelling it skids.
View SolutionA small box of mass m is placed on the outer surface of a smooth fixed sphere of radius R at a point where the radius makes a angle `Pse` with the vertical. The box is released from this position. Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA smooth sphere of radius R is moving in a straight line with an acceleration a. A particle is released from top of the sphere from rest. Find the speed of the particle when it is at an angular position `theta` from the initial position relative to the sphere.
View Solution
Illustration questions and complete solutions for chapter WORK, ENERGY AND POWER of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11