Complete Solutions to solved examples of chapter LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF MOTION |
| PRADEEP | solved examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A force of `5N` gives a mass `m_(1)`, an acceleration of `8 m//s^(2)`, and a mass `m_(2)`, an acceleration of `24 m//s^(2)`. What acceleration would it give if both the masses are tied together?
View SolutionA bullet of mass `100 gram` moving with `20 m//s` Strikes a wooden plank and penetrates upto 20 cm. Calculate the resistance offered by the wooden plank .
View SolutionA bus starts from rest accelerating unifromly with `4 ms^(-2)` . At `t = 10 s` ,a stone is dropped from the window of the bus 2 m high . If `g = 10 m//s^(2)` , what are the magnitude of velocity and acceleration of the stone at 10 .2 s ?
View SolutionAn astronaut accidentally gets separated out his small spaceship accelerating in interstellar space at a constant rate of `100ms^(-2)` . What is the acceleration of the astronaut the instant after he is outside the spaceship? (Assume that there are no nearby stars to exert gravitional force on him)
View SolutionThe motion of a particle of mass m is described by `y =ut + (1)/(2) g t^(2)` . Find the force acting on the particale .
View SolutionA balloon has a mass of 10 gram in air. The air escapes from the balloon at a unifrom rate with a velocity of `5 cm //s` and the balloon shrinks completely in 2.5 s . Calculate the average force acting on the balloon.
View SolutionTwo bodies A and B each of mass m are fixed together by a massless spring . A force F acts on the mass B as shown in fig .3 (a)18. At the instant shown , the body A has an acceleration a What is the acceleration of B ?

View SolutionA hydrogen gas filled ballon having a mass of 25 g is released up in air . As the ballon descends , the gas starts leking from it with a unifrom velocity of `12 cm//s` and as a result the balloon shrinks completely in 5 s . Find the average force acting on the ballon .
View SolutionForces of `sqrt 2 N` and `6 sqrt 2 N` are acting on a body of mass 10 kg at an angle of `60^(@)` to each other . Find the acceleration , distance covered and velocity of the body after 10 second , if the body is initially at rest .
View SolutionA bullet of mass 0.04 kg moving with a speed of `90 ms^(-1)` enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View SolutionA batsman hits back a ball straight in the direction of the bowler without changing its initial speed of `12 ms^(-1)` . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
View SolutionA ball moving with a momen - tum of `15 kg ms^(-1) ` strickes against the wall at an angle of `30 ^(@)` and is reflected back with the same momentum at the same angle . Calculte impulse.
View SolutionA cricket ball of mass 150 kg is moving with a velocity of `12 m//s` and is hit by a bat so that ball is turned back with a velocity of `20 m//s` . The force of the blow acts for 0.01 s on the ball . Find the average force exerted by the bat on the ball.
View SolutionA force acting on a body of mass 2 kg varies with time as shown in fig . 20 find impulse of the force and final velocity of the body.
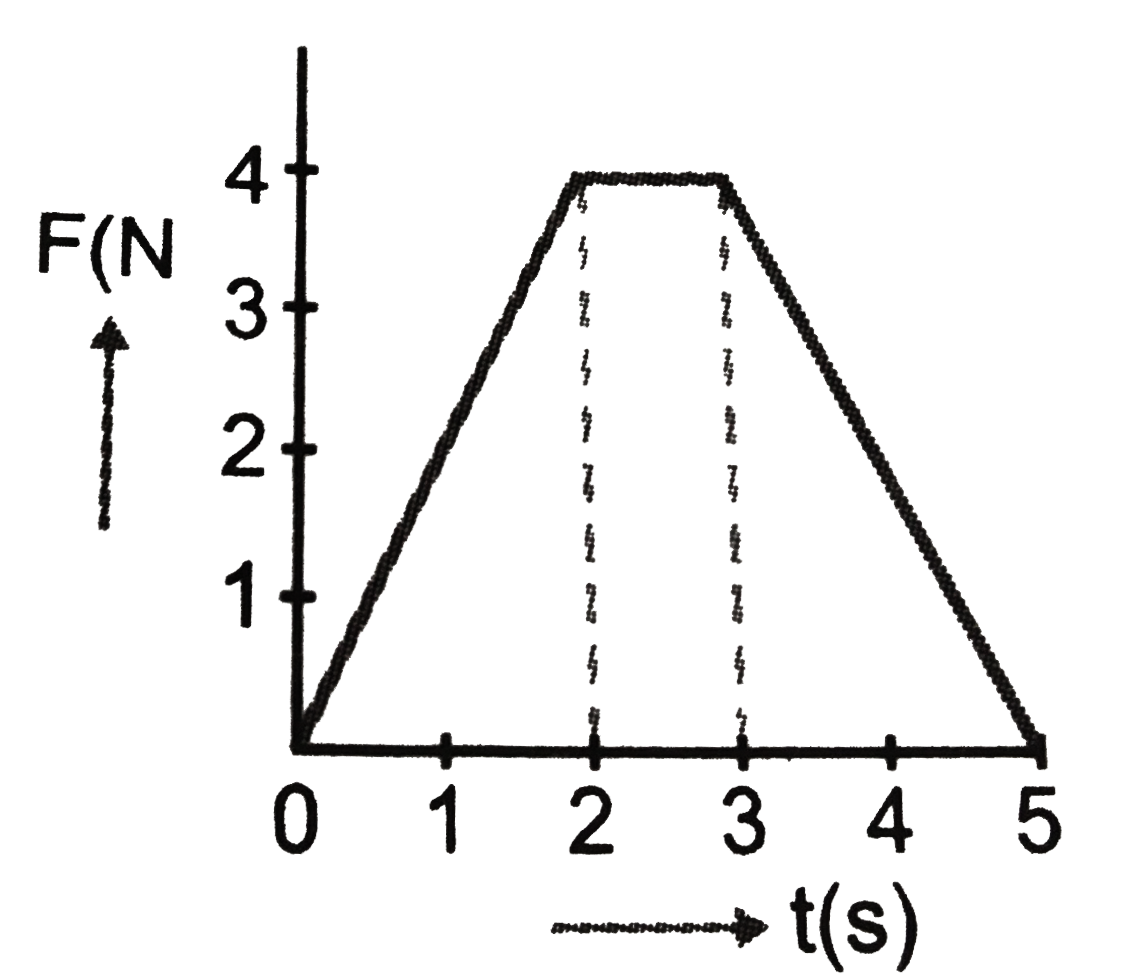
View SolutionA machine gun has a mass of 20 kg . It fire 20 gram bullets at the rate of 300 bullets per second at a speed of `250 m//s` . What force must be applied on the gun to keep it in position ?
View SolutionTwo identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View SolutionA ball of mass 0.2 kg travelling in a straight line with a speed of `m//s` along negative x- axis id deflected by a bat `15 m//s` along negative x - axis is deflected by a bat at an angle of `30^(@)` If the speed of the ball after deflection is `10 m//s`, find the impulse on the ball.
View SolutionAn elevator weighing 5000 kg is moving upward and tension in the supporting cable is 5000 N . Find upward acceleration . Starting from rest , how far does it rise in 10 secound ?
View SolutionFind the appared weight of a man weighing 49 kg on earth, when he is standing in a lift which is (i) rising with an acceleration of `1.2 m//s^(2)` (ii) going down with same acceleration (iii) falling freely under gravity (iv) going up or down with unifrom velocity . Take `g= 9.8 m//s^(2) `. \
View SolutionA 70 kg man in sea is being lifted by a helicopter with the help of a rope , which can bear a maximum tension of 100 kg wt . With what maximum acceleration the helicopter should rise so that the rope does not break ? Take `g = 9.8 m//s^(2)` .
View SolutionA lift of mass 2000 kg is supported by thick steel ropes . If maximum upward acceleration of the lift be `1.2 m//s^(2)` , and the breaking stress for the ropes be
`2.8 xx 10^(8) Nm^(-2)`
what should be the minimum diameter of rope ?
View SolutionA lift starts from rest with a constant upward acceleration It moves 1.5 m in the first 0.4 A person standing in the lift holds a packet of 2 kg by a string Calculate the tension in the string during the motion .
View SolutionA lift is going up. The total mass of the lift and the passengers is 1500 kg . The variation in the speed of the lift is given by the graph shown in Fig . What will be the tension in the rope pulling the lift at (i) `t = 1 s` , (ii) `t =6 s` (iii) `t = 11 s` ?
What is the height to which the lift takes the passengers ? During the course of entirs motion What is the average velocity and average acceleration of the lift ? Taken `g = 9.8 m//s^(2) `
 .
.
View SolutionFig show two bodies A and B of masses 2.5 kg and 2.8 kg respectively from a rigid support by two inextensible wires each of length 1.8 m . The upper wire is of negligible mass and lower wire is of mass `1.5 kg // m` . If the entire system moves upwards with an acceleration of `2 m//s^(2)`, find tension (i) at middle point p of upper wire (ii) at middle point Q of lower wire . Take `g =10 m//s^(2)`
.
View SolutionA machine gun has a mass of 10 kg . It fires 30 gram bullets at the rate of 6 bullets per secound with a speed of `400 m//s` . What force must be to the gun to keep it in position ?
View SolutionA hunter has a machine gun that can fire 50 g bullets with a velocity of `150 m//s` . A 60 kg tiger springs at him with a velocity of `10 ms^(-1)` How many bullets must the hunter fire per secoud into the tiger in order to stop him in his track.
View SolutionA man weighing `60kg` runs along the rails with a velocity of `8km//h` and jumps into a car of mass 1 quintal standing on the rails. Calculaate the velocity with which car will start travelling along the rails.
View SolutionA car of mass one metric ton travelling at `32m//s`c dashes into the rear of a truck of mass `8000kg` moving in the same direction with a velocity of `4m//s` After the collision the car bounces back wards with a velocity of `8m//s` What is the velocity of the truck after the impact ?
View SolutionA dise of mass 10 g is kept floating horizontally by throwing 10 marbles per secound against it from below . If mass of each marble is 5 g Calculate the velocity with which marbles are striking the disc . Assume that marbles strike the disc . Normally and rebound downwards with the same speed.
View SolutionA body of mass 1 kg at rest explodes into three fragments of masses in the ratio 1 : 1 : 3 . The two pieces of equal mass fly in mutually perpendicular directions with a speed of `30 m//s` each . What is the velocity of the heavier fragment ?
View SolutionA machine gun fires a bullet of mass 40 g with a velocity `1200 ms^-1`. The man holding it can exert a maximum force of 144 N on the gun. How many bullets can be fire per second at the most?
View SolutionA hunter has a machine gun that can fire 50 g bullets with a velocity of `150 m//s` . A 60 kg tiger springs at him with a velocity of `10 ms^(-1)` How many bullets must the hunter fire per secoud into the tiger in order to stop him in his track.
View SolutionA rocket has a mass of `2 xx10 ^(4)` kg of which half is fuel Assume that the fuel is consumed at a constant rate as the rocket is fired and there is contact thrust of `5 xx 10^(6)` N neglecting air resistance and any possible variation of g comput (i) the intial acceleration (ii) acceleration just when the whole fuel is consumed .
View SolutionCalculate the ration `m _(0)//m` for a rocket if it is to escape from the earth . Given escape velocity `= 11.2 km//s ` and exhaust speed of gases is `2 km// s` .
View SolutionA rocket is set for vertical firing If the exhaust speed is `1200ms^(-1)` , how much gas must be ejected per second to supply the thrust needed (i) to overcome the weight of rocket (ii) to give to the rocket an initial vertical upward acceleration of `29.6 m//s^(2)` Given mass of rocket = 6000 kg.
View SolutionA ballon of mass m is rising up with an acceleration a show that the fraction og weight of balloon that must be detached in order to double its acceleration , assuming the upthrust of air to remain the same
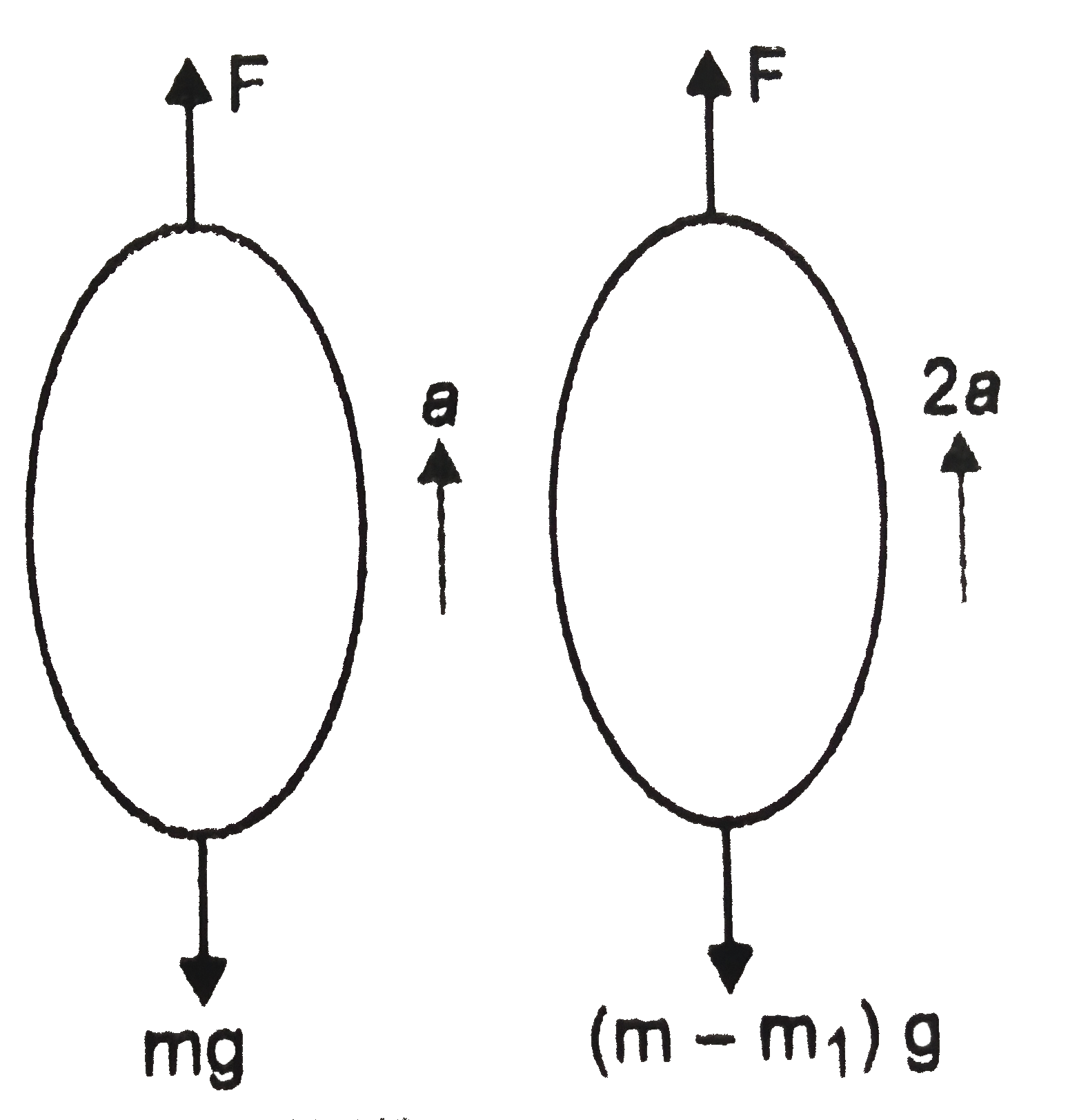
View SolutionA rocket motor consumes 100 kg of fuel per second exhausting it with a speed of `6 xx 10^(3) ms^(-1)` What thrust is exerted on the rocket ? What will be the velocity of the rocket at the instant its mass is reduced to `(1 // 40)` of its initial mass ? Take initial velocity of rocket as zero . Neglect gravity .
View SolutionA rocket burns 0.5 kg of fuel per second ejecting it as gases with a velocity of `1600 m//s` relative to the rocket . How much force is exerted on the rocket ? Also , calculate the velocity attainted by the rocket , when its mass
reduces to `(1)/(200)` th of its initial mass .
View SolutionA ballon of mass m is rising up with an acceleration a show that the fraction og weight of balloon that must be detached in order to double its acceleration , assuming the upthrust of air to remain the same

View SolutionA train is moving along a horizontal track . A pendulum suspended from the roof makes an angle of `4^(@)` with the vertical . If `g = 10 m//s^(2)` , what is the acceleration of the train ?
View SolutionA body of mass m is suspended by two strings making angles `alpha and beta` with the horizontal. Find the tensions in the strings.
View SolutionA body `m_(1)` of mass 10 kg is placed on a smooth horizontal table It is connected to a string which passes over a frictionless pulley and carries at the other end , a body `m_(2)` of mass 5 kg What acceleration will be produced in the bodies when the nail fixed on the table is removed ? what will be the tension in the string during the motion of the bodies ? What when the bodies stop ? (g= 9.8 N ? kg ) .
View SolutionA mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = `10 ms^(-2)`) . Neglect mass of the rope .
View SolutionThe masses `m_(1) m_(2)` and `m_(3)` of the three bodies shown in fig . Are 5 , 2 and 3 kg respectively Calculate the valuse of tension `T_(1) T_(2)` and `T_(3)` when (i) the whole system is going upward with an acceleration of `2 m//s^(2)` (ii) the whole system is stationary ` (g=9.8 m//s^(2))` .
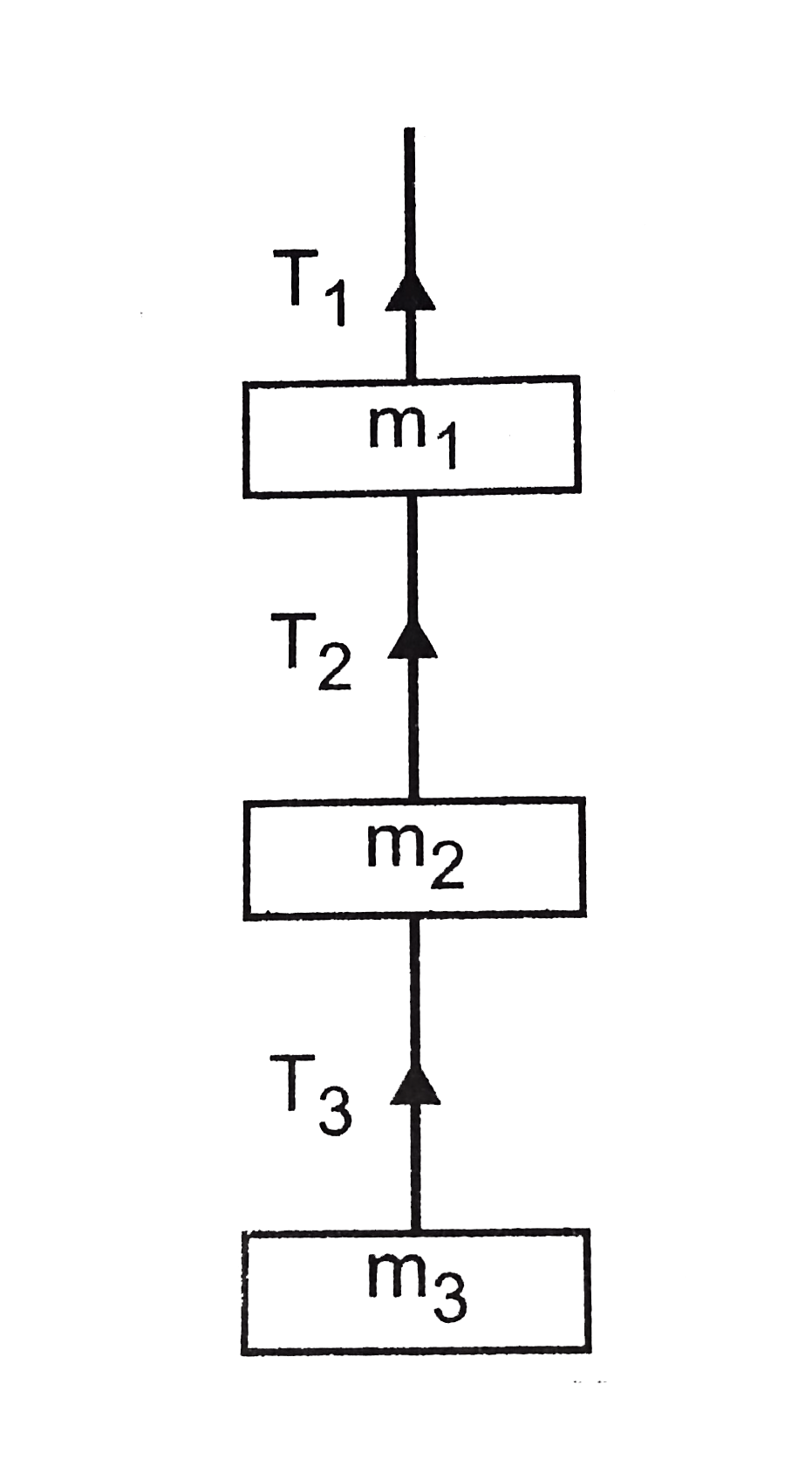 .
.
View SolutionWhat is the tension in a rod of length length L and mass M at a distance y from`F_(1)` when the rod is acted on by two unequal force `F_(1)` and `F_(2) ( lt F_(1))` as shown in.
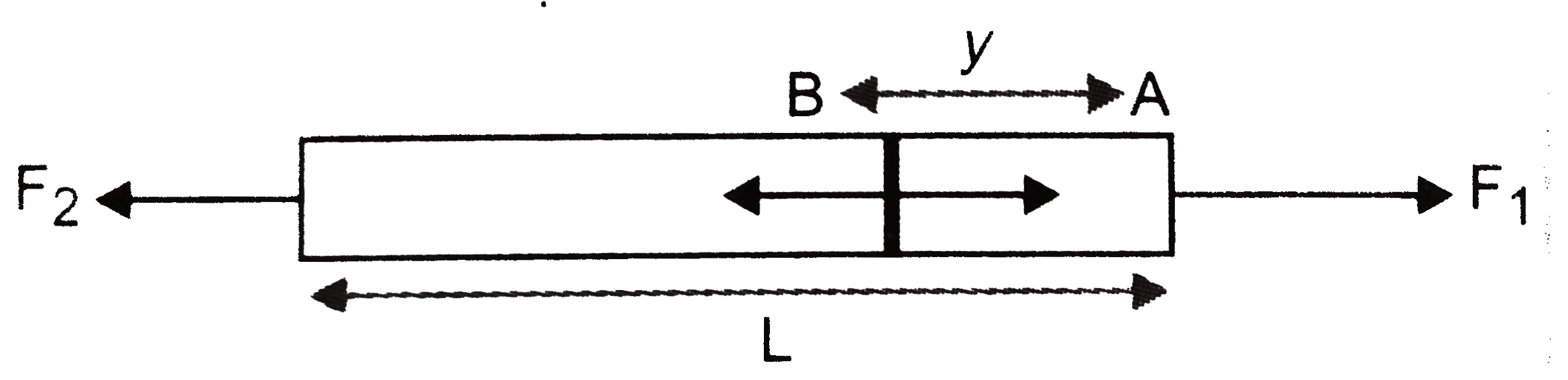
View SolutionTwo blocks of masses `2.9 kg` and `1.9 kg` are suspended from a rigid support `S` by two inextensible wires each of length `1 m` , as shown in figure.The upper wire has negligible mass and the lower wires and support have an uniformly distributed mass of `0.2 kg` .The whole system of blocks, wire and support have an upwards acceleration of `0.2 m//s^(2)`. Acceleration due to gravity is `9.8 m//s^(2)`.
(a) Find the tension at the mid point of the lower wire.
(b)Find the tension at the mid point of the upper wire.

View SolutionThe pulley arrangements of fig (a) and (b) are identical. The mass of the rope is negligible. In (a) the mass m is lifted up by attaching a mass 2 m to the other end of the rope. In (b) m is lifted up by pulling the other end of the rope with a constant downward force F = 2 mg. Which of the following is correct?

View SolutionA pull of 15 N is applied on a rope attached to a block of mass 7 kg lying on a smooth horizontal surface. forcs exerted on the rope by the block ?
View SolutionA block of mass 100 kg is set into motion on a frictionless horizontal surface with the help of a frictionless pulley and rope system shown in What horizontal force should be applied on the rope to produce an acceleration of `0.1 m//s^(2)`
 .
.
View SolutionTwo blocks of masses 50 kg and 30 kg connected by a massless string pass over a light frictionless pulley and rest on two smooth planes inclined at angles `30^(@)` and `60^(@)` resp . With horizontal .Determine the accelertion in the two blocks and tension in the string `g = 10 m//s^(2)` .
View SolutionA block of weight 20 N is placed on a horizontal table and a tension T is applied on the block . Tension can be increased to 8 N before the block begins to slide . A force of 4 N keeps the block moving at constant speed , once it has been set in motion . Find the coefficients of static friction and kinetic friction].
View SolutionThe coefficient of friction between the ground and the wheels of a car between the ground and the wheels of acar moving on a horizontal road is 0.5 If the car starts from rest , what is the minimum distance in which it can acquire a speed of `72 km // h` ? take `g = 10 ms^(-2)` .
View SolutionIn the masses of A and B are 10 kg and 5 kg . Calculate the minimum mass of C which may stop A from slipping Coefficient of static friction between block A and table is 0.2
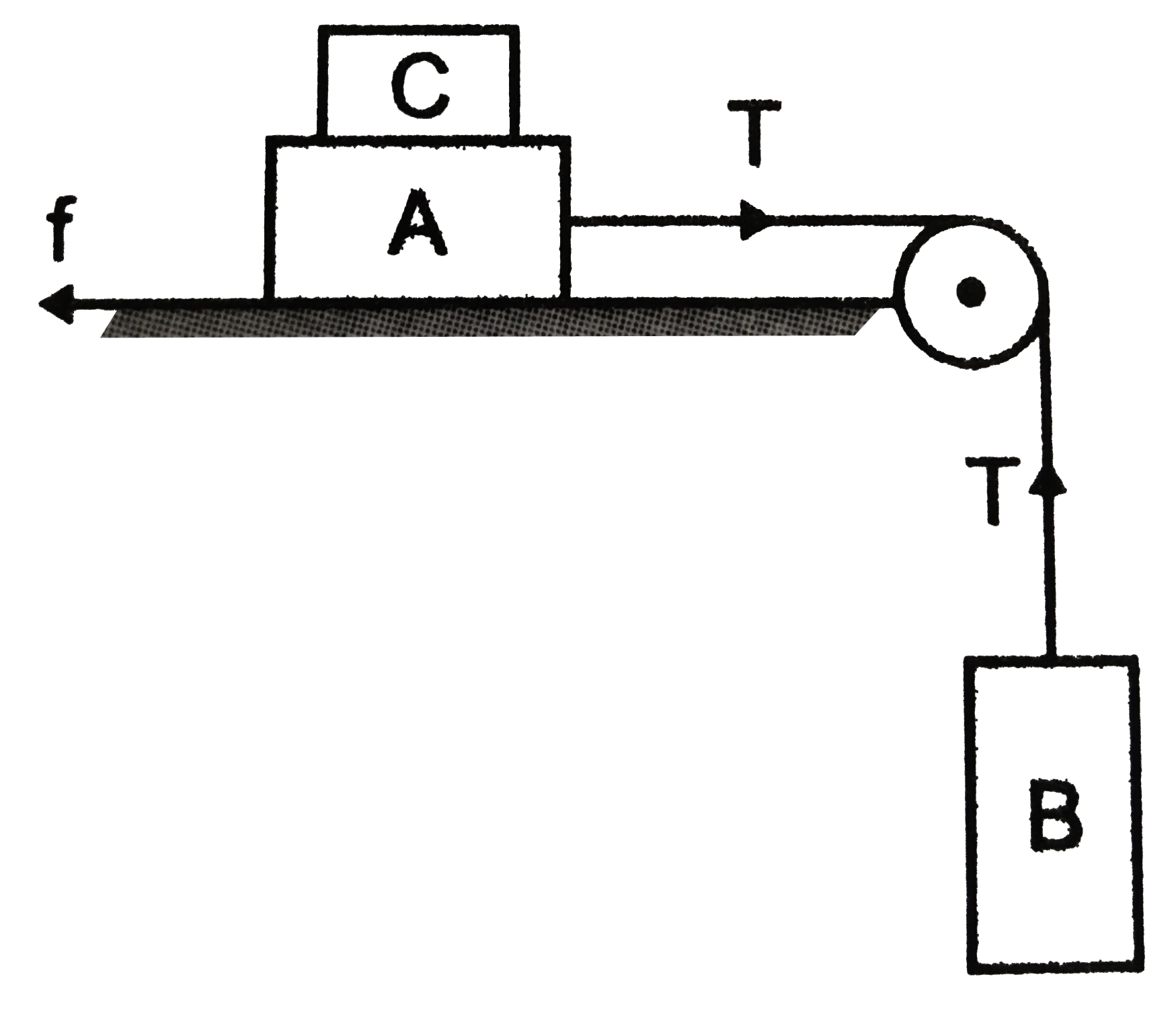 .
.
View SolutionA body rolled on ice with a velocity of `8 ms^(-1)` comes to rest after travelling a distance of 4 m . Calculate the coefficient of friction .
View SolutionDetrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given `g = 10 m//s^(2)` .
View SolutionWhat is the acceleration of the block and trolley system shown in if the coefficient of kinetic friction between the trolley and the surface is 0 .04 ? What is the tension in the string ? Take `g = 10 ms^(-2)` Neglect the mass of the string
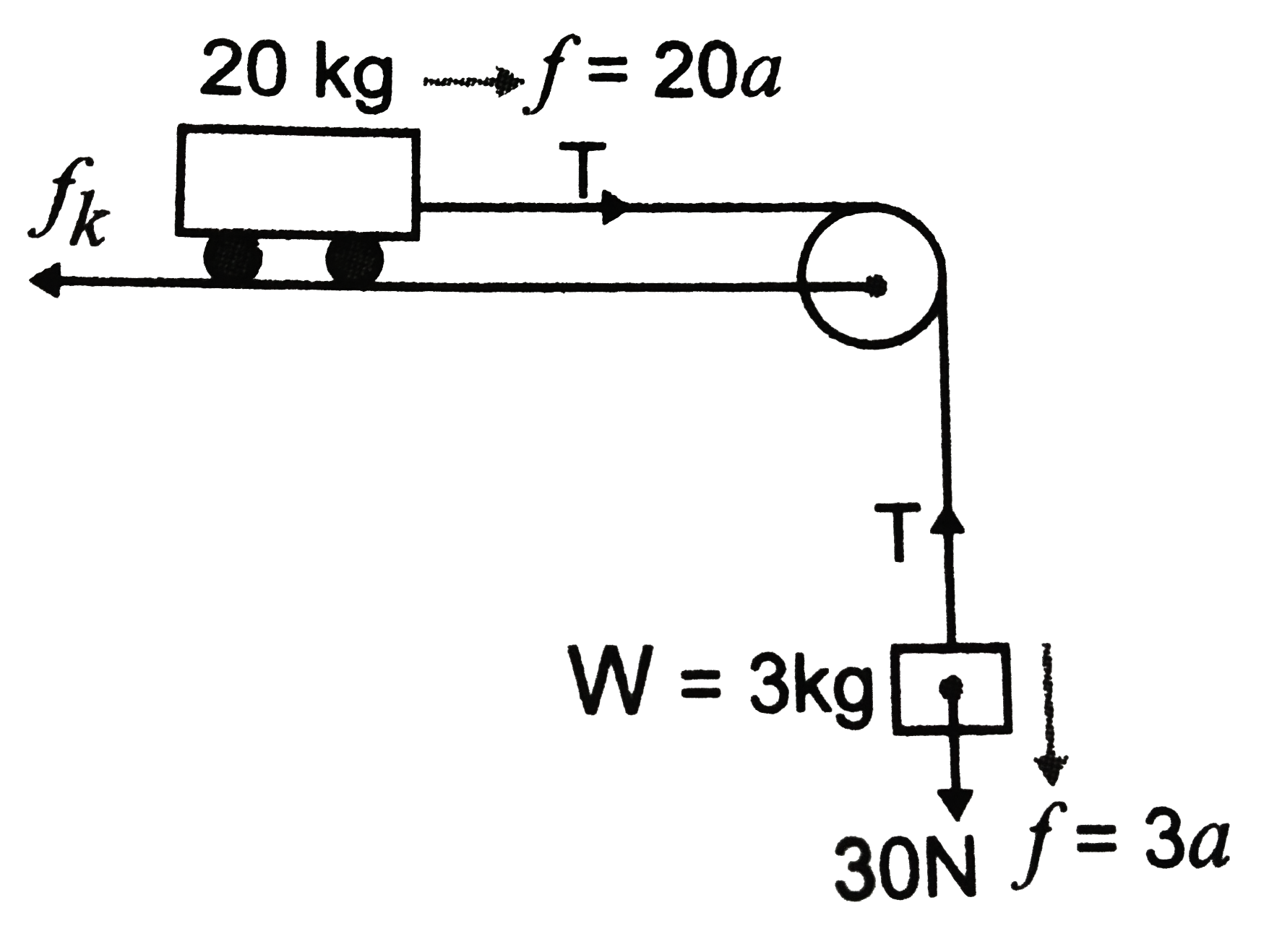 .
.
View SolutionA block the of mass `4kg` is placed on another block of mass `5kg` and the block `B` rests on a smooth horizontal table for sliding the block `A` on `B` a horizontal force `12N` is required to be applied force on it How much maximum horizontal force can be applied on 'B' s that both `A` and `B` move together? Also find out the accleration proudced by this force
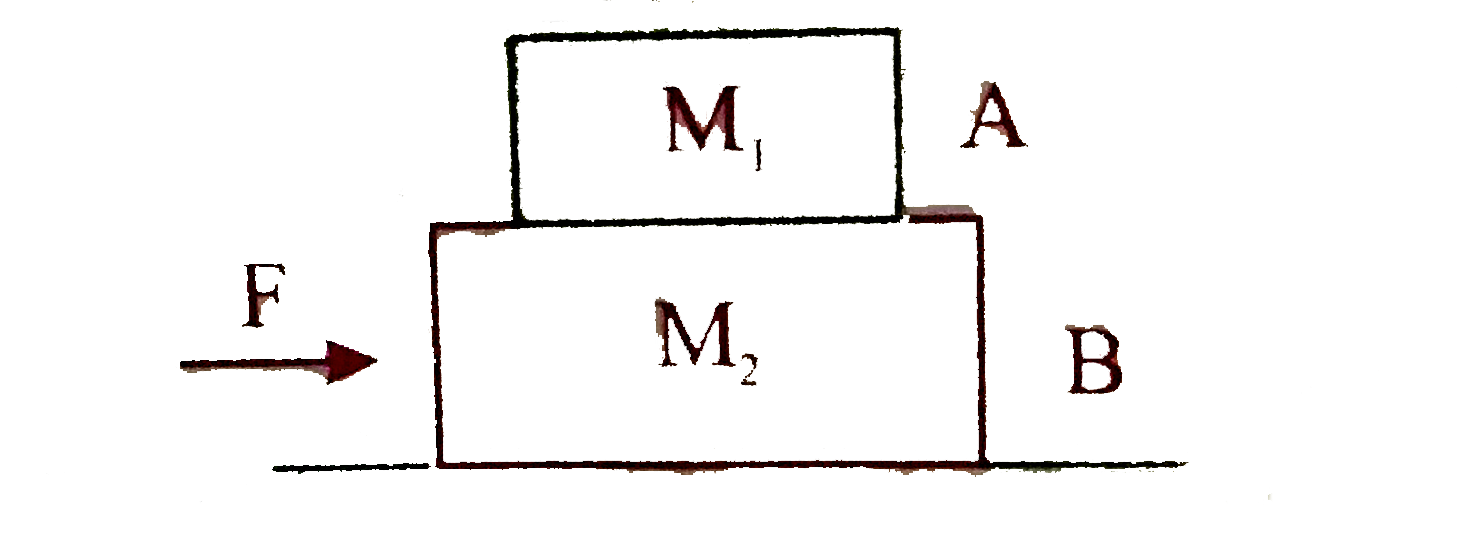 .
.
View SolutionA particle of mass m rests on a horizontal floor with which it has a coefficient of static friction `mu`. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has to be applied.
View SolutionA bullet of mass 0.01 kg is fired horizontal into a 4 kg wooden block block at rest , on a horizontal surface. The coefficient of kinetic friction between the block and surface is 0.25 the combination moves 20 m before coming to rest . With what speed did the bullet strike the block ?
View SolutionA cubical block rests on an inclined plance of `mu = (1)/sqrt(3)` . Determine the angle at which the block just slides down the incline .
View SolutionA block of mass 10 kg is sliding on a surface inclined at `30^(@)` with horizontal . If coefficient of friction between the block and the surface is 0.5 , find acceleration produced in the block . Take ` g = 9.8 m //^(2)` .
View SolutionFind the force required to move a train of mass `10^(5)` kg up an incline of 1 in 50 with an acceleration of `2 ms^(-2)`. Coefficient of friction between the train and rails is 0.005. Take `g = 10^(2)`.
View SolutionA railway engine weighing 40 metric ton is travelling along a level track at a speed of `54 km H^(-1)` What additional power is required to maintain the same speed up an incline of 1 in 49 Take `g = 9.8 m//s^(2)` and `m u = 0.1`.
View SolutionA block A of mass 14 kg moves alongg an inclined plance that makes an angle of `30^(@)` with the horizontal . This block is connected to another block B of mass 14 kg by a taut massless string that runs around a massless frictionless pulley . The block B moves down with constant velocity . Calculate force of friction and coefficient of kinetic friction .
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle `0 = 15^(@)` with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
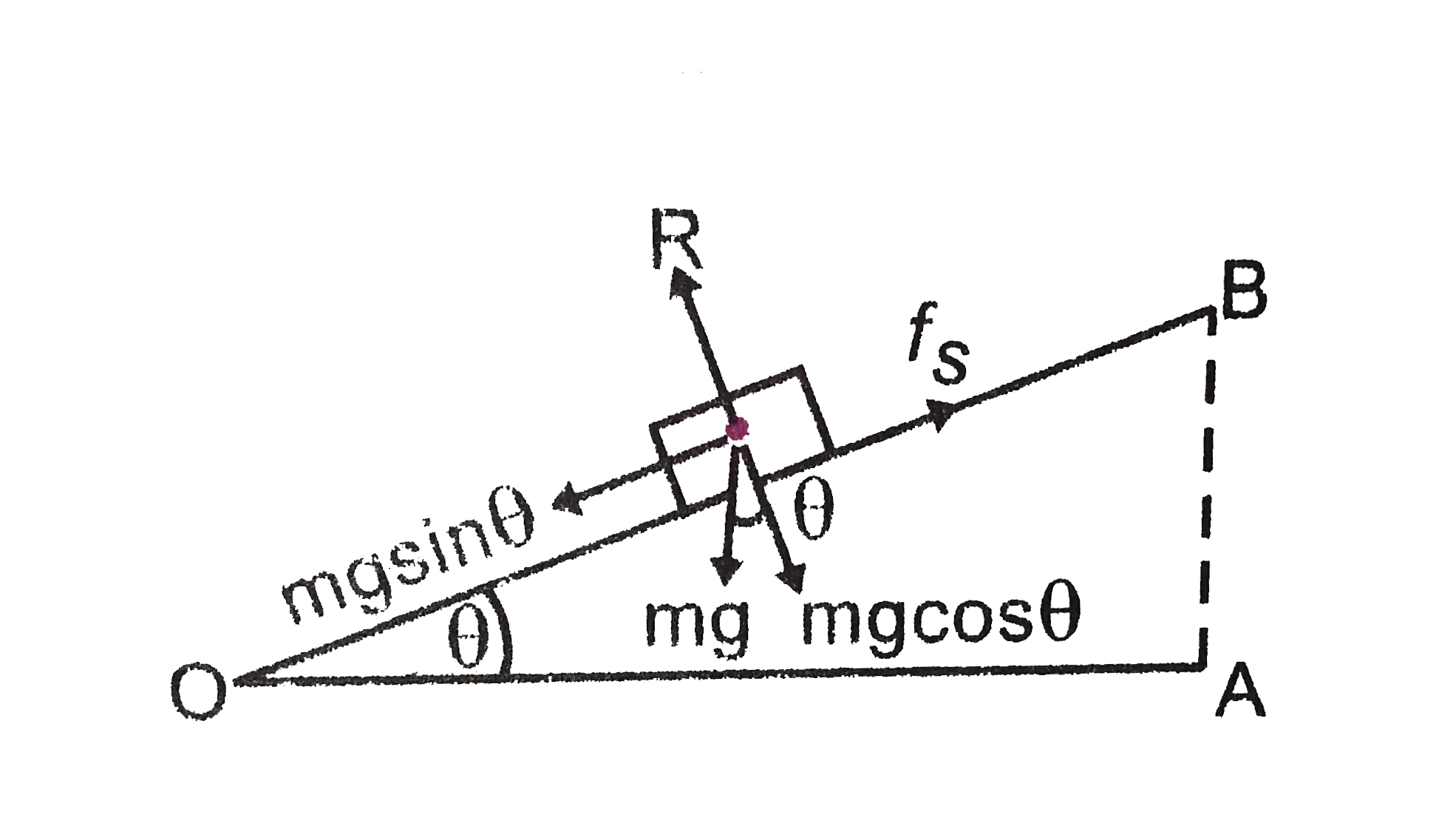
View SolutionAn engine of 100 H.P draws a train of mass 200 metric ton with a velocity of `36 km // h` . Find the coefficient of friction.
View SolutionA mass of 200 kg is placed on a rough inclined plane of angle `30^(@)` . If coefficient of limiting friction is `1 // sqrt 3` , find the least forces in newton , acting parallel to the plane (i) to keep the mass from sliding down (ii) to move the mass up the plane.
View SolutionFind the force required to move a train of 2000 quintals up an incline of 1 in 50 , with an acceleration of `2 ms^(-2)`, the force of friction being 0.5 newton per quintal.
View SolutionA piece of ics slides down a `45^(@)` incline in twice the time it takes to slide down a frictionless `45^(@)` incline . What is the coefficient of friction between the ice and the incline ? .
View SolutionTwo blocks `m_(1) = 4 kg` and `m_(2) = 2` kg connected by a weightless rod slide down a plane having an inclination of `37^(@)` . The coefficient of dynamic friction of `m_(1)` and `m_(2)` with the inclined plane are `mu_(1) = 0 .75` and `mu_(2) = 0 . 25` respectively Find the common acceleration of the two blocks and tension in the rod Take is `37^(@) = 0.6` and `cos 37^(@) = 0 .8` .
View SolutionAparticle of mass 1 g executes an oscillatory motion on the concave surface of a spherical dish of radius 2m placed on a horizontal plane, Figure . If the motion of the particle begins from a point on the dis at a height of 1 cm. from the horizontal plane and coefficient of friction is 0.01 , fing the total distance covered by the particle before coming to rest.

View SolutionA block of mental of mass 50 gram placed over an inclined plane at an angle of `15^(@)` slides down without acceleration . If the inclination is increased by `15^(@)` , what would be the acceleration of the block ?
View SolutionA body of mass 10 kg is placed on an inclined surface of angle `30^(@)` . If coefficient of limiting friction is `1 //sqrt3` , find the inclined plane. Force is being exerted parallel to the inclined plane
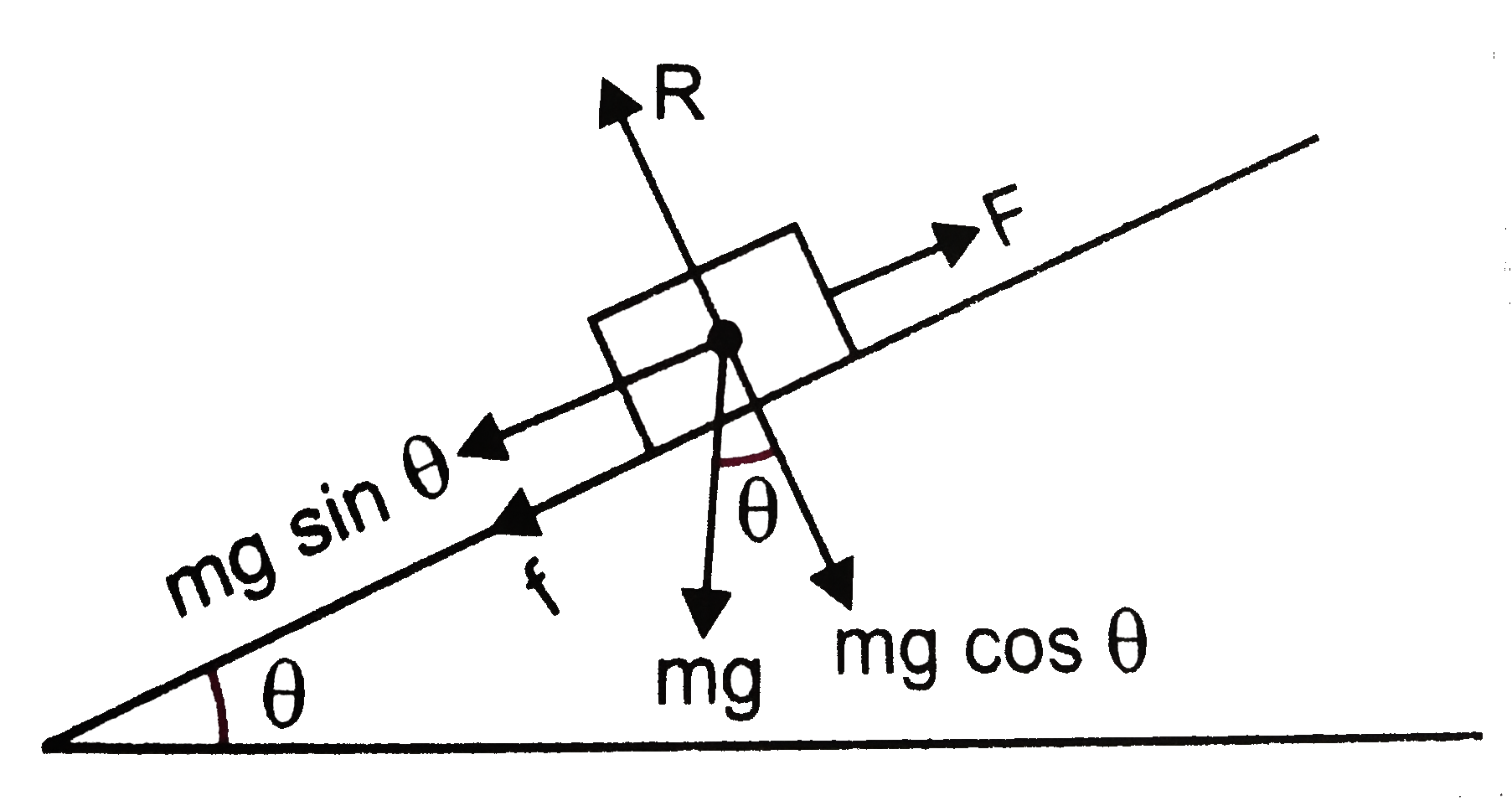 .
.
View SolutionA stone of mass 4 kg is attached to a string of 10 m length and is whirled in a horizontal circle . Calculate the max . Velocity with which the stone can be whirled if the string can withstand a maximum tension of 160 N .
View SolutionA gramophone disc rotates at 60 rpm . A coin of mass 18 g is placed at a distance of 8 cm from the centre . Calculate centrifugal force on the coin . Take `pi^(2) = 9. 87` .
View SolutionFind the maximum speed at which a car can turn round a curve of `30 m` radius on a level road if coefficient of friction between the tyres and road is `0.4. Take g = 10 m//s^(2)`.
View SolutionA string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle. Calculate the greatest number of revolutions that the mass can make without breaking the string.
View SolutionA car travels on a flat, circular track of radius `200 m` at `30 ms^(-1)` and has a centripetal acceleration `= 4 .5 ms^(-2)`. (a) If the mass of the car is 1000 kg , what frictional force is required to provide the acceleration ? (b) If the coefficient of static friction is 0.8, what is the maximum speed at which the car can circle the track ?
View SolutionTwo small wooden blocks are placed on a crircular rotating table of radius 1 m at distance 10 cm and 60 cm from the centre of the table the table is rotating with angular velocity `4 rad// s` , about the axis of rotation . Out of these two blocks , which one continues to revolve with the table ? Give `mu = 0.2 ` .
View SolutionA sphere of mass 200 g is attached to an inextensible string of length 130 cm whose upper end is fixed to the ceilling . The sphere is made to describe a horizontal circle of radius 50 cm Calculate the periodic time of this conical pendulum and the tension in the string .
View SolutionA particle describes a horizontal circle on the smooth inner surface of a conical funnel as shown in Fig. If the height of the plane of the circle above the vertex is `9.8 cm`, find the speed of the particle.
View SolutionA curve in a road froms an are of radius 800 m If the road is 39.2 m wide Calculate the safe speed for turning if outer edge of the road is 0.5 m higher than the inner edge .
View SolutionA cyclist riding at a speed of `14 sqrt(3 ) ms^(-1)` takes a turn around a circular road of radius `20 sqrt(3)` m . What is his inclination with horizontal ?
View SolutionA cyclist speeding at `6 m//s` in a circle of 36 m diameter makes an angle 0 with the verticl . What is the value of 0 ? Also , deter - mine the minimum possible value of the coefficient of friction between the tyres and the road .
View SolutionA car is speeding on a horizontal road curving round with a radius 60 m The coefficient of friction between the wheels and the road in 0.5 The height of centre of gravity of the car from the road level is 0.3 m and the distance between the wheels is 0 .8 m . Calculate the maximum safe velocity for negotiating the curve . Will the car skid or topple if this velocity is exceeded ?
View SolutionFind the angle through which a cyclist bends when he covers a circular path `34.3 m` long in `sqrt (22)` sec . Given `g = 9.8 ms^(-2)` .
View SolutionA cyclist speeding at `18 km// h` on a level road takes a sharp circular turn of radius 3 m without reducing the speed . The coefficient of static friction between the tyres and the road is 0.1 Will the cyclist slip while taking the turn ?
View SolutionA circular racetrack of radius 300 m is banked at an angle of `15^(@)` If the coefficient of friction between the wheels of a race car and the road is 0.2 what is the (a) optimum speed of the race car to avoid wear and tear on its tyres , and (b) maximum permissible speed to aviod slipping ?
View SolutionA circular race track of radius 400 m is banked at an angle of `10^(@)` . If the coefficient of friction between the wheels of a race car and the road is 0.2 , what is the (i) optimum speed of the race car to aviod wear and tear on its tyres .
maximum permissible speed to aviod slipping ?
View SolutionA railway carriage has its CG at a height of 1 m above the rails , which are 1 m apart . Calculate the maximum safe speed at which it can travel round an unbanked curve of radius 80 m .
View SolutionA stone is tied to a weightless string and revolved in a vertical circle of radius 5 m . What should be the minimum speed of the stone at the highest point of the circle so that the string does not slack ? What should be the speed of the stone at the lowest point of vertical circle ? Take ` g = 9.8 ms^(2) ` .
View SolutionA bucket containing water is tied to one end of a rope of length 2.5 m and rotated about the other end in a vertical circle so that water does not spill even when bucet is upside down . What is the maximum velocity of the bucket at which this happens ? How many rotations per minute is it making `g = 10 m//s^(2) ` .
View SolutionIn a circus , the diameter of globe of death is 20 m . From what minimum height must a motor cyclist start in order to go around the globe successfully ? .
View SolutionA small stone of mass 200 g is tied to one end of a string of length 80 cm . Holding the other end in hand , the stone is whirled into a vertical circle What is the minimum speed that needs to be imparted at the lowest point of the circular path , so that the stone is just able to complete the vertical circle ? what would be the tension at the lowest point of circular path ? ` (Take g = 10 m//s^(2)) ` .
View SolutionA massless string of length 1.2 m has a breaking strength of 2 kg wt . A stone of mass 0.4 kg tied to one end of the string is made to move in a vertical circle by holding the other end in hand . Can the particle describe the vertical circle ? Take `g = 10 ms^(-2)`.
View SolutionA small stone of mass 0.2 kg tied to a massless , inextensible string is rotated in a vertical circle of radius 2 m If the particle is just able to complete the vertical circle what is its speed at the highest point of the circular path ? How would the speed get affected if the mass of the stone is increased by 50% ? Take ` g = 10 m//s^(2) ` .
View SolutionA particle of mass 150 g is attached to one end of a massless inextensible string It is made to describe a vertical circle of radius 1 m When the string is making an angle of `48.2^(@)` with the vertical , its instantaneous speed is ` 2 m//s ` What is the tension in the string in this position ? Whould this particle be able to complete its circular path ? .
View SolutionA bucket containing 4 kg of water , is tied to a rope of length 2.5 m and rotated in a vertical circle in such a way that the water in upside down position What is the speed of the bucket at (a) highest point and (b) lowest point of its circular path ? Take ` g= 10 m//s ` .
View SolutionShown a smooth looping the loop track A particle of mass m is released from oint A , as shown If H = 3 r , whould the particle loop the loop ? What is the force on the circular track when the particle is at point (i) B (ii) C ? .
View SolutionA child revolves a stone of mass 0 .5 kg tied to the end of a string of length 40 cmin a vertical circle . The speed of the stone at the lowest point of the circle is `3 m//s` Calculate tension in the string at this point.
View Solution
solved examples questions and complete solutions for chapter LAWS OF MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS LAWS OF MOTION
- Additional Examples / Exercises
- Advanced problems for competitions
- Assertion- Reason Type Questions
- conceptual problmes
- Curiosity Question
- EXERCISES
- Fill in the blanks
- Higher order thinking skills
- Integer Type Questions
- JEE (Main and Advanced)/ Medical Entrance Special
- Long Answer Questions
- Multiple Choice Questions
- Problems for practice
- sample problems
- Short Answer Questions
- Short Answer Questions
- solved examples
- Value Based Questions with Answers
- Very short answer questions