Complete Solutions to QUESTIONS of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP | QUESTIONS |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Two forces `50N and 100 N` are acting on a rod capable of rotating it about `O` as shown in Fig. What is the net torque acting on the rod ?

View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of `(3v^2)/(4g)
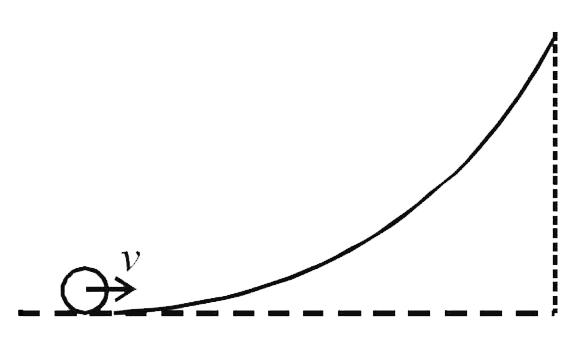
with respect to the initial position. The object is
View SolutionA circular plate of unifrom thickness has a diameter of `56 cm`. A circular portion of diameter `42 cm` is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA stone of mass m tied to the end of a string is whirled around in a horizontal circle (neglect force du eto grvaity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then the tension in the given by `T = A r^(n)`, where `A` is a constant and `r` is instantaneous radius of the circle. Show that `n = - 3`.
View SolutionA threaded rod with `12 turns//cm` and diameter `1.18 cm` is mounted horizontal. A bar with a threaded hole to match the rod is screwed onto the rod. The bar spins at `216 rev//min`. How long will it take for the bar to move `1.50 cm` along the rod ?
View SolutionFind the centre of mass of `a` unifrom disc of radius a from which a circulr section of radius `b` has been removed. The centre of hole is at a distance `c` from the centre of the disc.
View SolutionA solid cylinder of mass `20 kg` and radius `0.12 m` rotating wit initial angula speed of `125 rad//s` is placed lightly (i.e. without any translational push) on a horizontal table with coefficient of kinetic friction `mu_(k) = 0.15` between the cylinder and the table.
(a) After how long does the cylinder start rolling ?
(b) What is the initial translational energy, rotational energy and total energy of the cylinder ?
(c) What is the final (i.e. after rolling begins) translational energy, rotational energy and total energy of the cylinder ? (d) Is the finl total enrgy equal to the initial total energy of motion of the cylinder ? If not, where does the difference of energy disappear ?
(e) Account for the loss of total energy of motion in the following way : find the work done by friction on the body its translational motion. Show that net work done by friction on the body is negative, equal in magnitude to the loss of total energy calculated in (d) above.
View SolutionPoint masses `m_(1) and m_(2)` are placed at the opposite ends of a rigid rod of length `L`, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point `P` on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity `omega_(0)` is minimum, is given by :
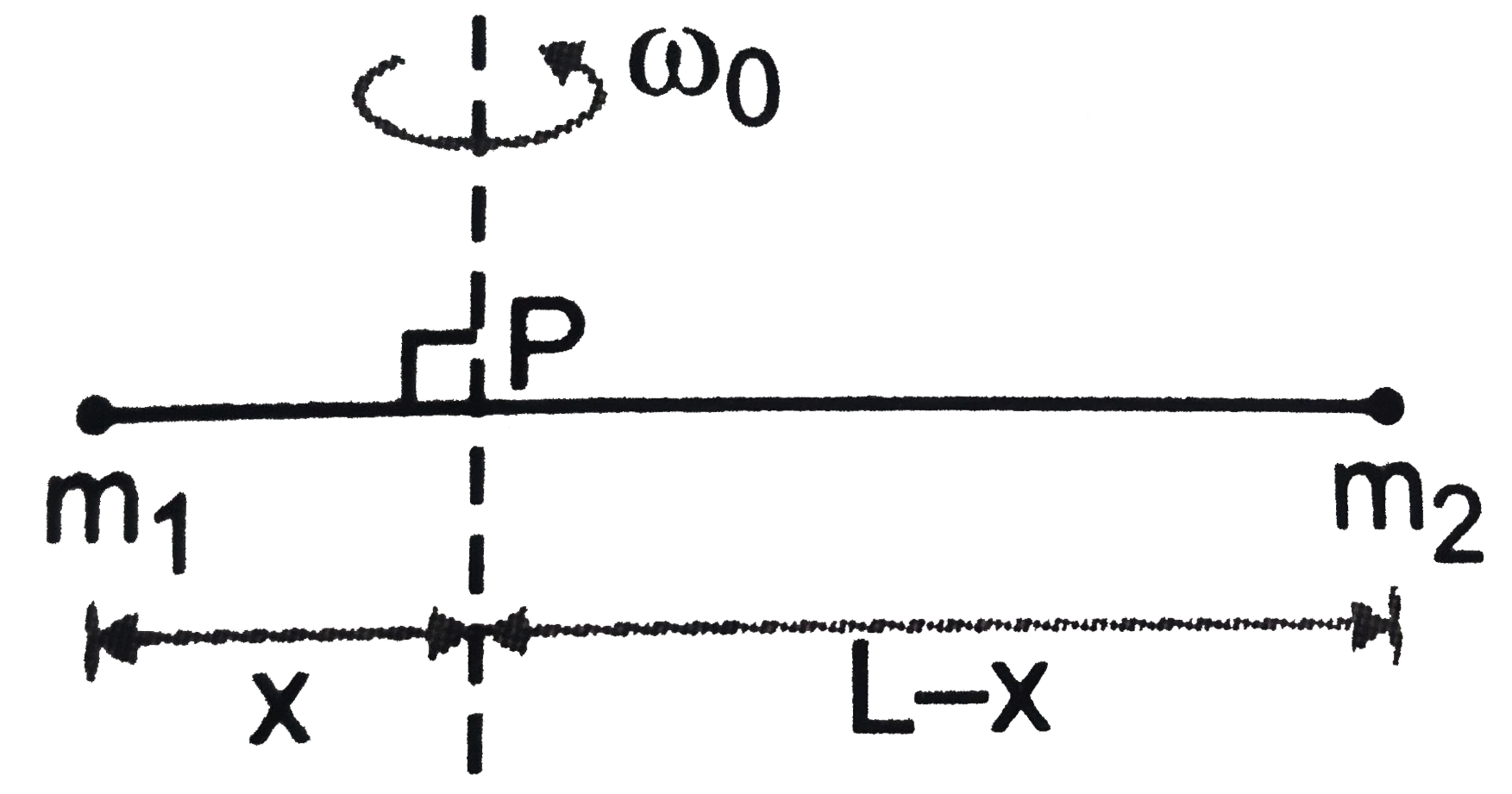
View SolutionA ball of mass `10^(-2) kg` and having charge `+ 3 xx 10^(-6)C` is tied at one end of a `1m` along thread. The other end of the thread is fixed and a charge `- 3 xx 10^(-6) C` is placed at this end. The ball can move in the circulr orbit of radius `1m` in the vertical plane. Initially, the ball is at the bottom. Find the monimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.
View SolutionThree particles, each of the mass `m` are situated at the vertices of an equilateral triangle of side `a`. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation `a`. Find the initial velocity that should be given to each particle and also the time period of the circular motion. `(F=(Gm_(1)m_(2))/(r^(2)))`
View SolutionFrom a uniform circular disc of diameter `d,a` circular disc of diameter `d//6` and having centre at a distance `d//4` from the centre of the disc is scooped out. Determine the centre of mass of remaining portion.
View SolutionA spot light `S` rotates in a horizontal plane with a constant angular velocity of `0.1 rad//s`. The spot of light `P` move along the wall at a disatnce `3 m`. What is the velocity of the spot `P` when `theta = 45^(@)` ?
View SolutionA nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of `60^(@)` with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.
View SolutionA uniform sphere of mass `m` and radius `R` is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when `h = 7R//5`.
View SolutionA carpet of mass `M` is rolled along its length so as to from a cylinder of radius `R` and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to `R//2`.
View Solution
QUESTIONS questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion- Reason Type questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- FILL IN THE BLANKS
- Focus Multiple Choice Questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- Multiple Choice Questions Comprehension 2
- Multiple Choice Questions II.
- Multiple Choice Questions III. Comprehension 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- NCERT
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- QUESTIONS
- Sample problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.