Complete Solutions to MULTIPLE CHOICE QUESTIONS of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP | MULTIPLE CHOICE QUESTIONS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The centre of mass of a body is moving with a uniform velocity of `10 cm//s`. Three forces are applied on the body, which are in equilibrium. The velocity of centre of mass would become
View SolutionA fire cracker following a parabolic path explodes in mid air. The centre of mass of all the fragments will follow a path
View SolutionThe correct relation between linear velocity `overset rarr(v)` and angular velocity `overset rarr(omega)` of a particle is
View SolutionObtain a expression for torque in polar co-ordinates.
View SolutionThe moment of linear momentum is called
View SolutionTo maintain a rotor at a uniform angular speed of `100 s^(-1)`, an engine needs to transmit a torque of `90 N-m`. The power of engine must be
View SolutionThe correct relation between torwue `tau` and angular momentum `L` is
View SolutionA rigid body is said to be in translational equilibrium, when its velocity `overset rarr(v)` is
View SolutionA rigid body is said to be in partial equilibrium, when it is in
View SolutionCalculate the angular velcity of the minute`s hand of a clock.
View SolutionMoment of inertia of a body depends upon
View SolutionFormation of a neutron star is explained on the basis of
View SolutionMoment of inertia of a uniform circular ring of mass `2 kg` and diameter `1 m` about its diameter is
View SolutionThe radius of gyration of a uniform circular disc of radius `R`, about any diameter of the disc is
View SolutionMoment of inertia of a hollow cylinder of mass `M` and radius `R`, about the axis of cylinder is
View SolutionKinetic energy of a body rolling without slipping is
View SolutionAcceleration of a solid cylinder rolling without slipping down an incline of inclination `theta` is
View SolutionThe rotational analgue of force is
View SolutionA grindstone of moment of inertia `6 kg m^(2)` is found to have a speed of `150` rpm, `10 sec`. After starting from rest. Torque applied is
View SolutionWhat would be the length of the day, if earth were to shrink suddenly to `1//64th` of its original volume ?
View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.
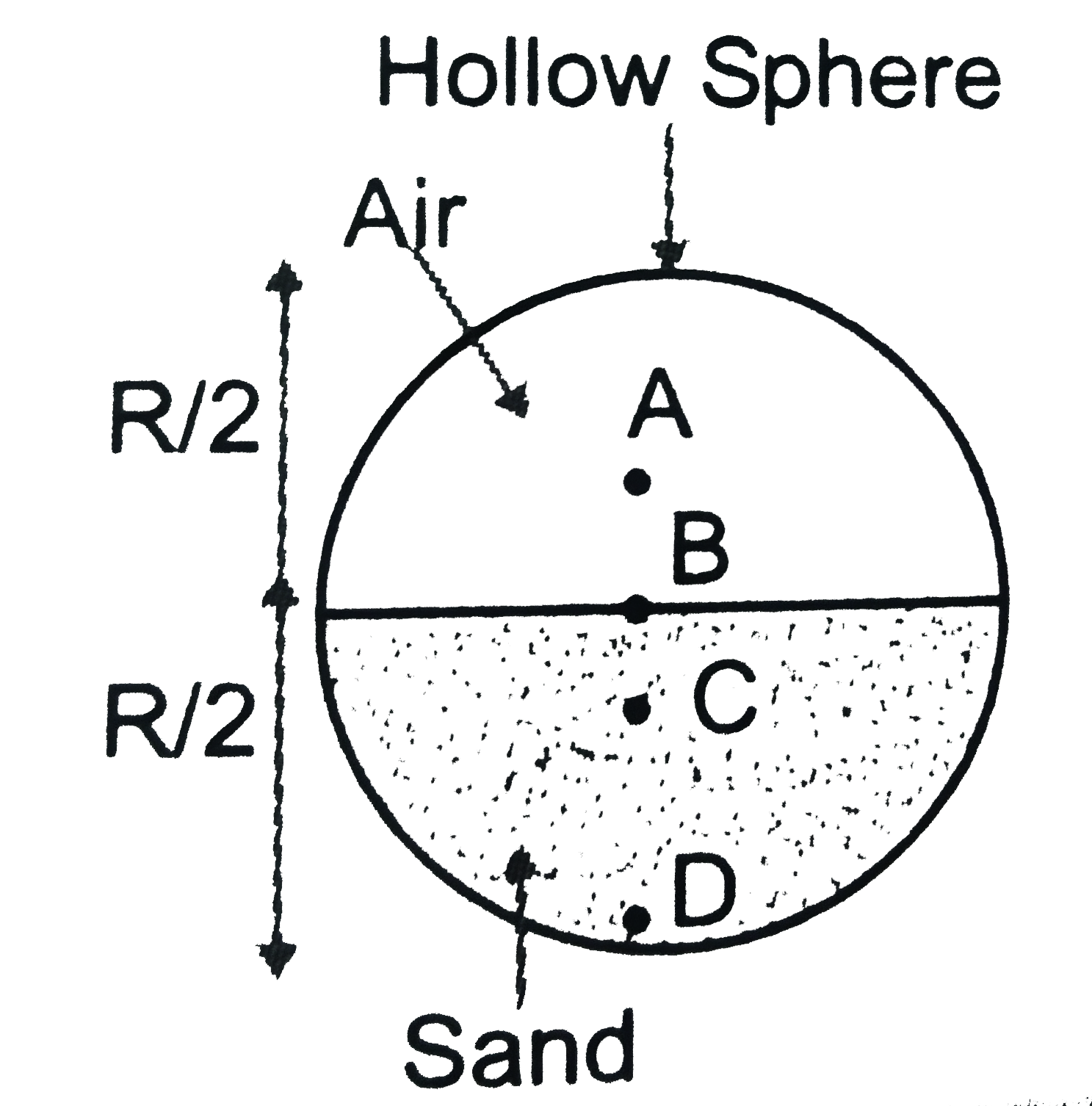
View SolutionA particle of mass `m` is moving in yz-plane with a unifrom velocity `v` with its trajectory running parallel to +ve y-axis and intersecting z-axis at `z = a` Fig. The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is :

View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
View SolutionA unifrom square plate has a small piece `Q` of an irregular shape removed and glued to the centre of the plate leaving a hole behind [Fig.] The moment of inertia about the z-axis is than
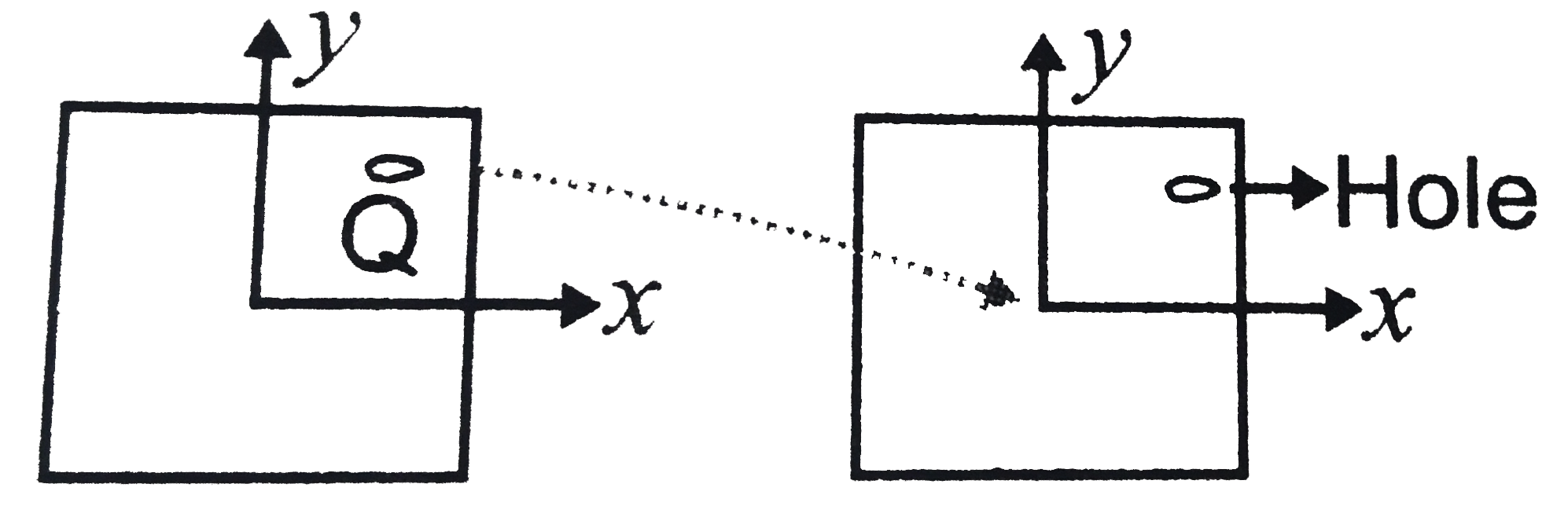
View SolutionIn problem `5, the CM` of the plate is now in the following quadrant of `x-y` plane.
View SolutionThe density of a non-uniform rod of length `1m` is given by `rho (x) = a (1 + bx^(2))`
where a and b are constants and `0 le x le 1`.
The centre of mass of the rod will be at
View SolutionA Meery -go-round, made of a ring-like plarfrom of radius `R and mass M`, is revolving with angular speed `omega`. A person of mass `M` is standing on it. At one instant, the person jumps off the round, radially awaay from the centre of the round (as see from the round). The speed of the round after wards is
View SolutionFigure shows two identical particles `1` and `2`, each of mass `m`, moving in opposite directions with same speed `vec V` along parallel lines. At a particular instant, `vec r_1` and `vec r_2` are their respective position vectors drawn from point `A` which is in the plane of the parallel lines. Which of the following is the correct statement ?
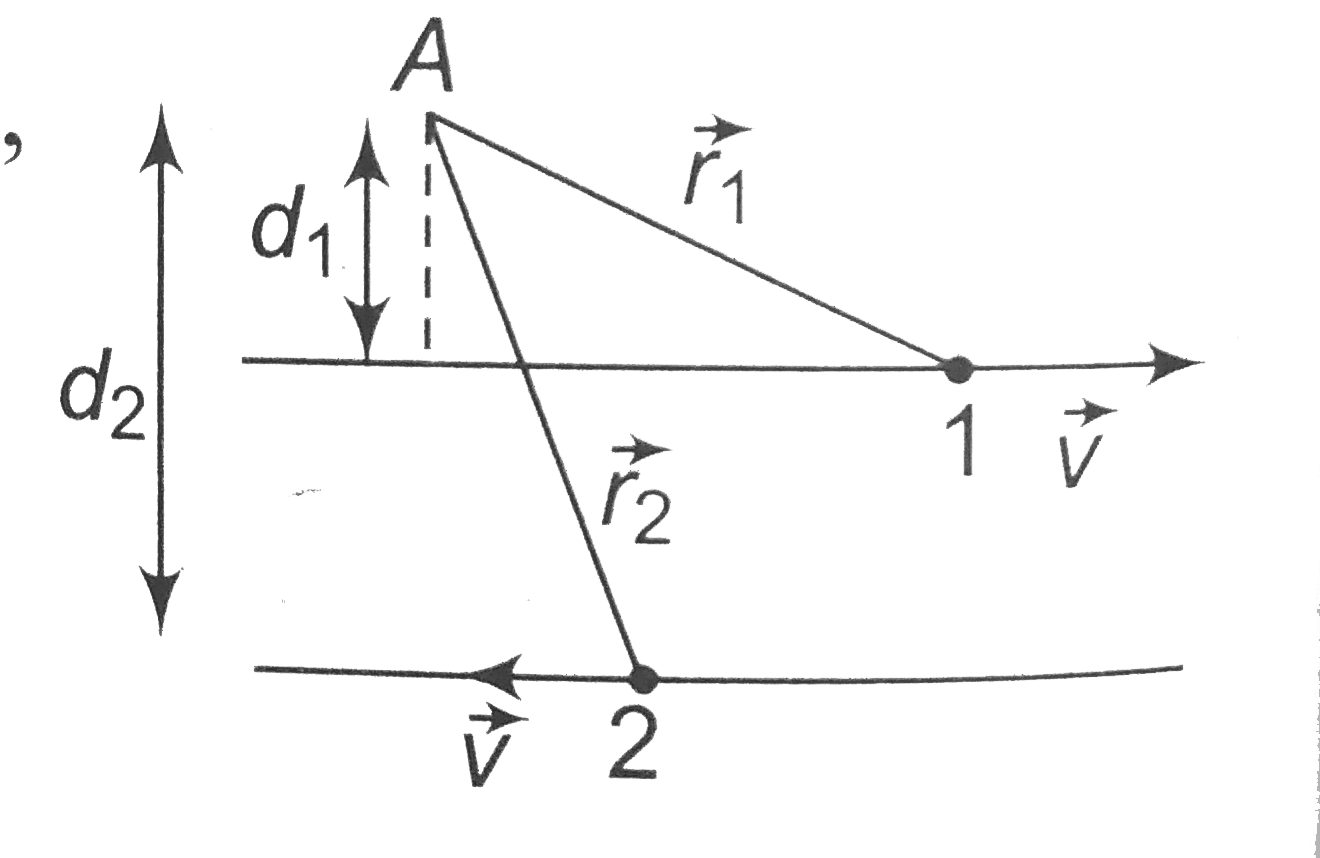 .
.
View SolutionThe net external torque on a system of particles about an axis is zero. Which of the following are compatible with it ?
View SolutionFigure shows a lamina in `x-y` plane. Two axes `z` and `z'` pass perpendicular to its plane. A force `F` acts in the plane of lamina at point `P` as shown. Which of the following statements is incorrect ?
(The point `P` is closer to `z'-axis` than the z-axis).
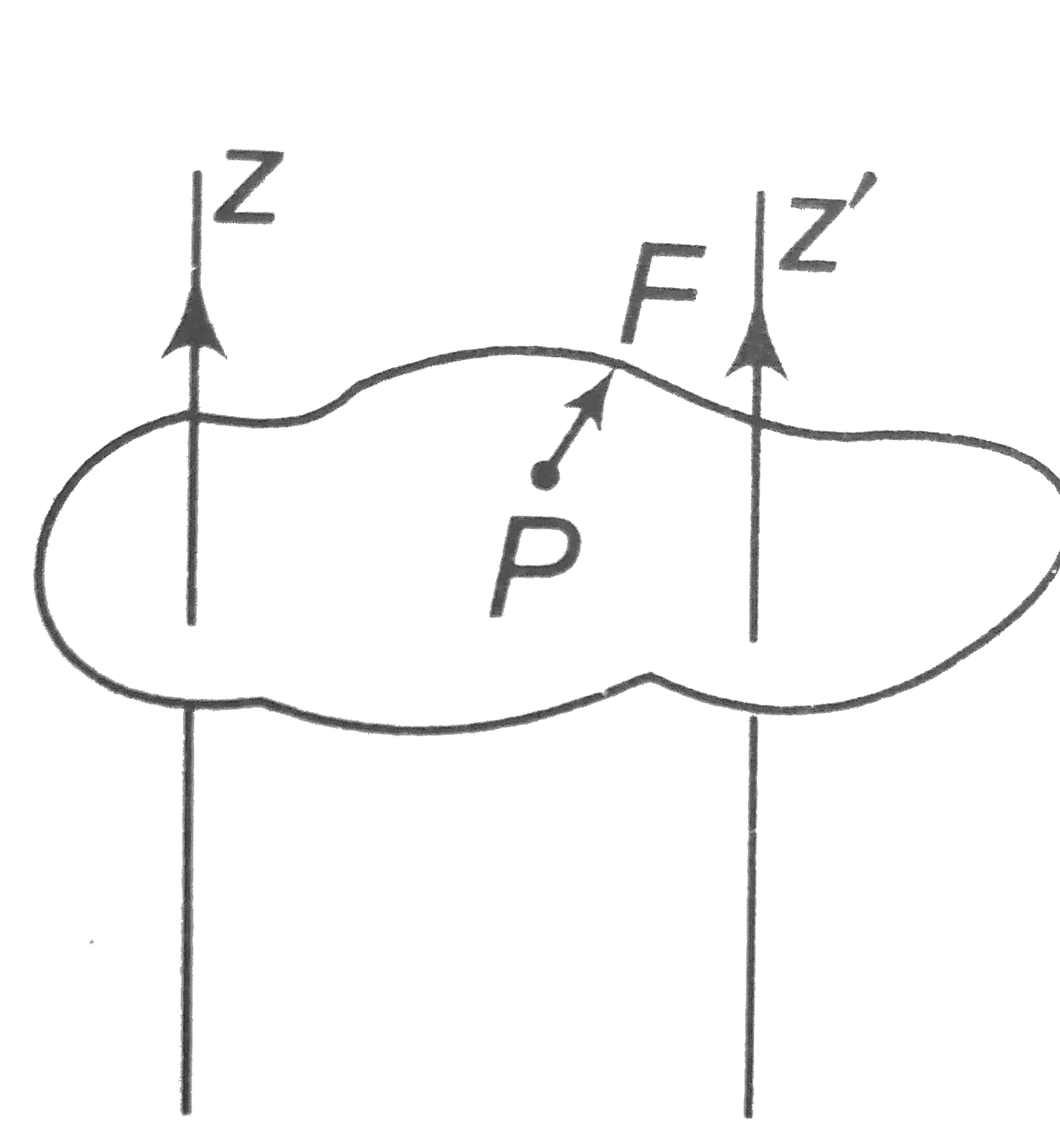 .
.
View SolutionWith reference to Fig. of a cube of edge a and mass m, state whether the following are true or false. (O is the centre of the cube.)
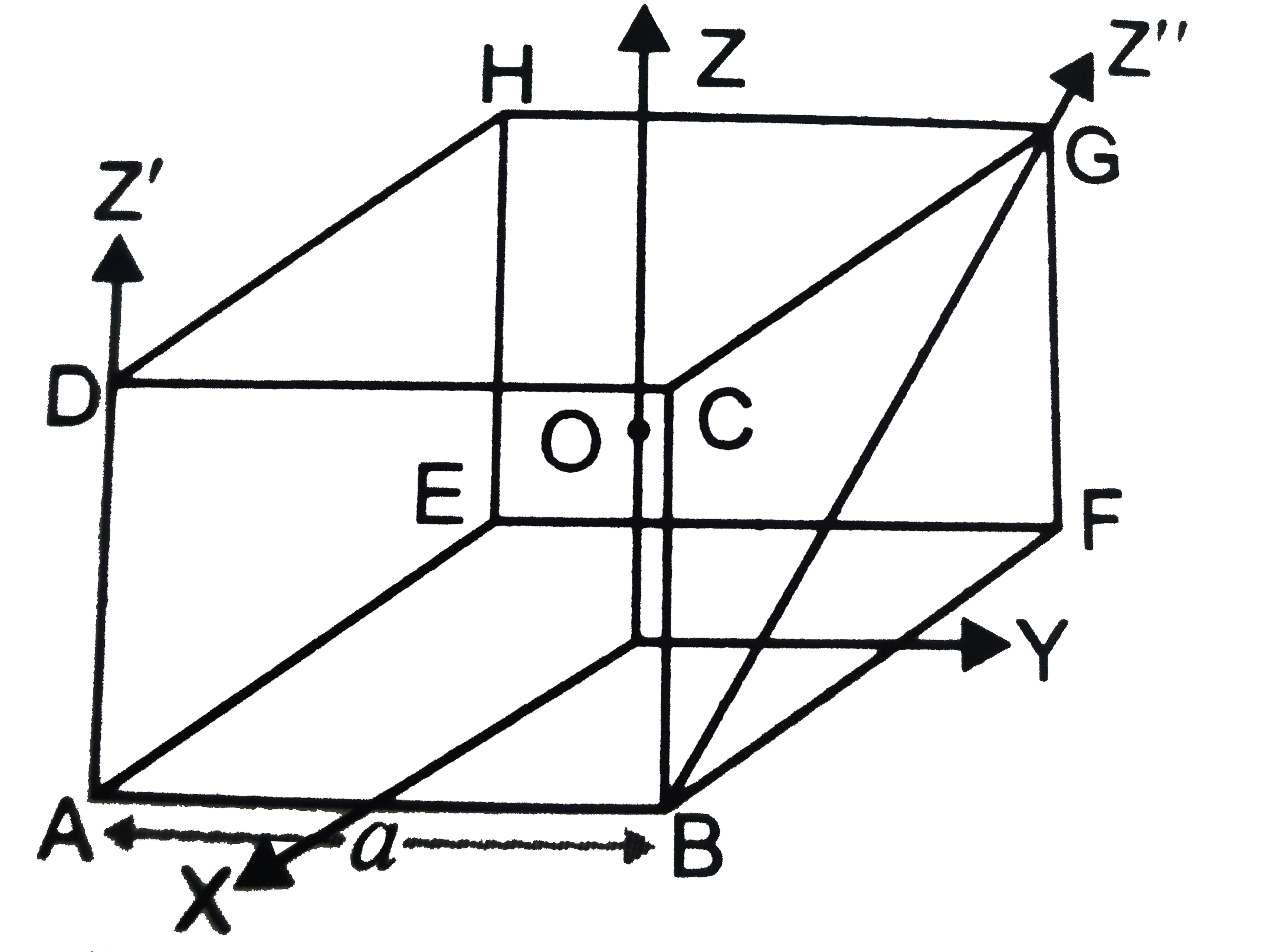
View SolutionA rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......
View SolutionThree identicle particle each of mass `1 kg` are placed with their centres on a straight line. Their centres are marked `A, B and C` respectively. The distance of centre of mass of the system from `A` is.
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is `alpha/R` from the center of the bigger disc. The value of `alpha` is
View SolutionA thin rod of length 'L' is lying along the `x`-axis with its ends at `x=0` and `x=L` its linear (mass/length) varies with `x` as `k((x)/(L))^n`, where n can be zero of any positive number. If to position `x_(CM)` of the centre of mass of the rod is plotted against 'n', which of the following graphs best apporximates the dependence of `x_(CM)` on n?
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is `omega`. Its cenre of mass rises to a maximum height of :
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution(1) Centre of gravity (C.G.) of a body is the point at which the weight of the body acts,
(2) Centre of mass coincides with the centre of gravity if the earth is assumed to have infinitely large radius,
(3) To evaluate the gravitational field intensity due to any body at an external point, the entire mass of the body can be cosidered to be concentrated at its C.G..,
(4) The radius of gyration of any body rotating about ab axis is the length of the perpendicular dropped from thr C.G. the body to the axis. which one of the following paires of statements is correct ?
View SolutionConsider a two particle system with particles having masses `m_1 and m_2` if the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle is moved, so as to keep the center of mass at the same position?
View SolutionFrom a disc of radius `R and mass M`, a circular hole of diameter `R`, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
View SolutionA disc and a solid sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
View SolutionFrom a disc of radius `R` and mass `M`, a circular hole of diameter `R`, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
View SolutionThe densities of two solid spheres A and B of the same radii R very with radial distance `r as p_A(r ) = k ((r )/(R )) and p_B(r ) = k((r )/(R )^5,` respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are `I_A and I_B` respectively. if `(I_B)/(I_A) = (n)/(10),` the value of n is
View SolutionFrom a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View SolutionThree idential spherical shells each of mass `m` and radius `r` are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
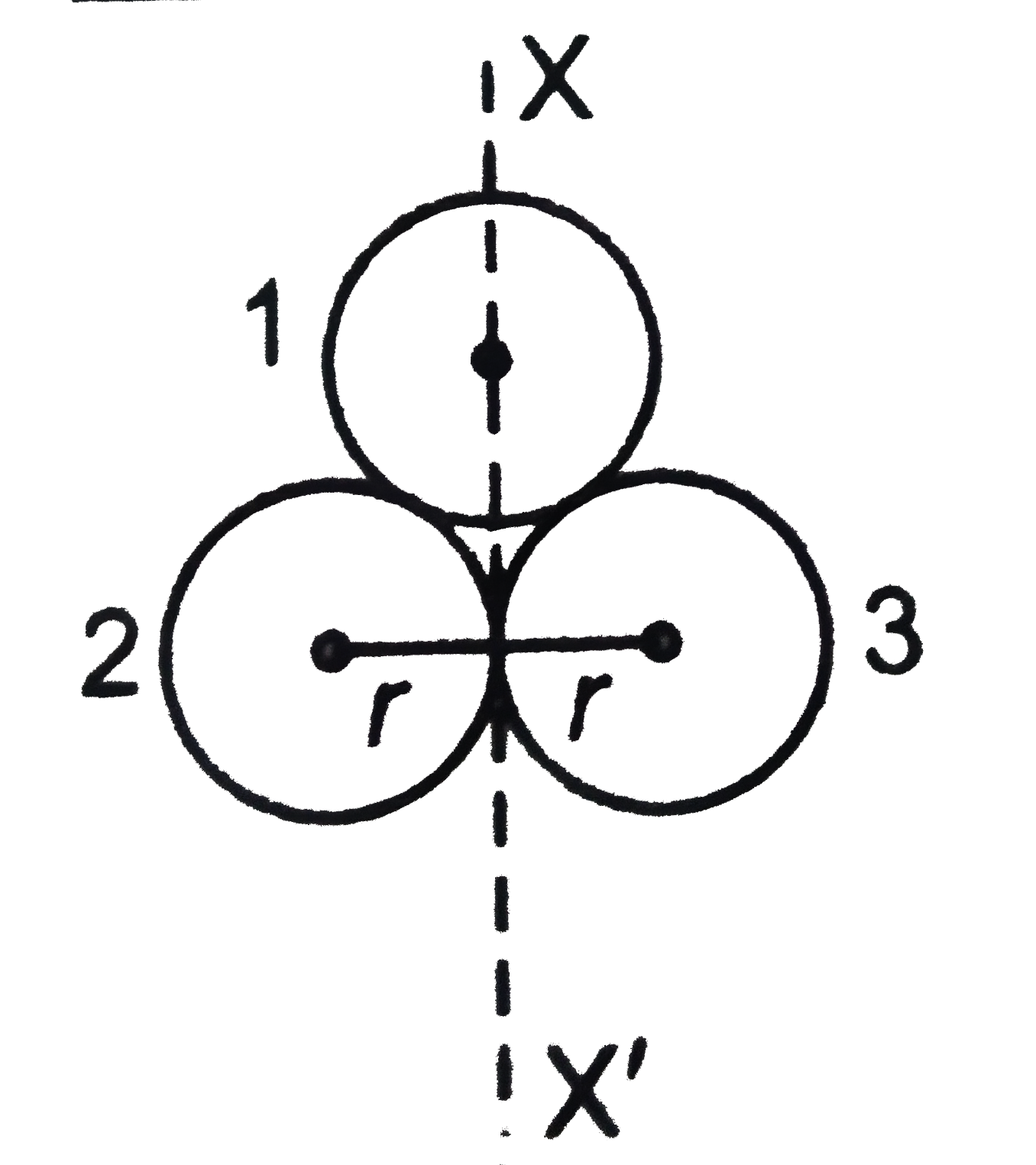
View SolutionPoint masses `m_(1) and m_(2)` are placed at the opposite ends of a rigid rod of length `L`, and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point `P` on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity `omega_(0)` is minimum, is given by :
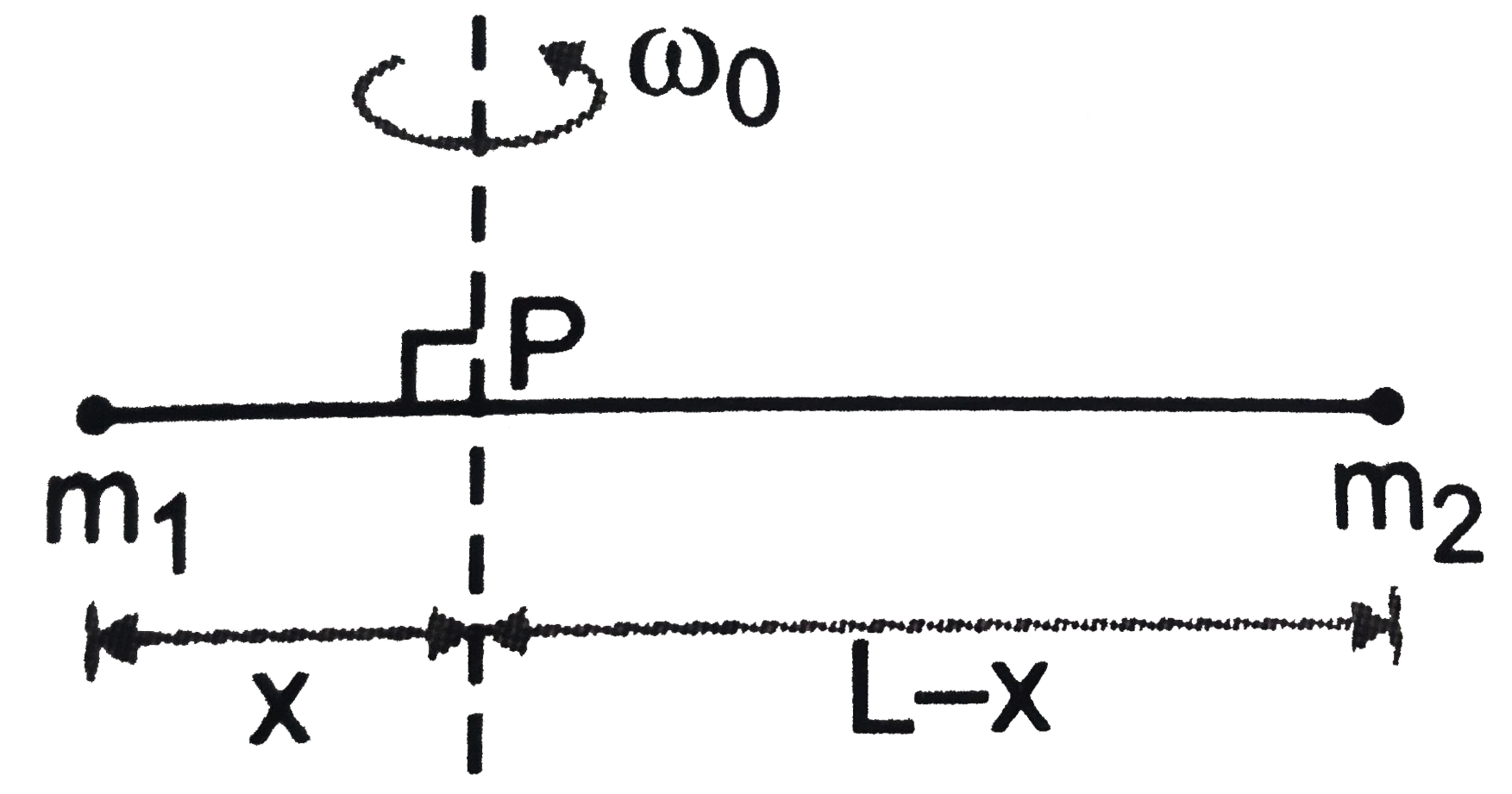
View SolutionIf `l_(1)` is the moment of inertia of a thin rod about an axis perpendicular to its length and passing thorugh its centre of mass and `l_(2)` the moment of inertia of the ring formed by the same rod about an axis passing through the centre of mass of the ring and perpendicular to the plane of the ring. then find the ratio `(l_(1))/(l_(2))`.
View SolutionA raw egg and a hard boiled egg are made to spin on a table with the same angular speed about the same axis. The ration of the time taken by the two to stop is
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tengential axis in the plane of the ring is
View SolutionThree identical rods, each of length `L`, are joined to from a rigid equilateral triangle. Its radius of gyration about an axis passing through a corner and perpendicular to plane of triangle is
View SolutionConsider a uniform square plate of side 'a' and mass 'm' The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is
View SolutionFour identical thin rods each of mass `M` and length `l`, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionA circular disc of moment of inertia `I_(t)` is rotating in a horizontal plane about its symmetry axis with a constant angular velocity `omega_(i)`. Another disc of moment of inertia `I_(b)` is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed `omega_(f)`. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionFour solid spheres each of diameter `sqart5`cm and mass 0.5 kg are placed with their centers at the corners of a square of side 4cm. The moment is `Nxx10^(-4)kg - m^2` , then N is .
View SolutionA pulley has radius 2m is rotated about its axis by a force `F= (20 t- 5t^2)` newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is `10kg m^2` the number of rotations made by the pulley before its direction of motion is reversed, is:
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of `(3v^2)/(4g)` with respect to the initial position. The object is
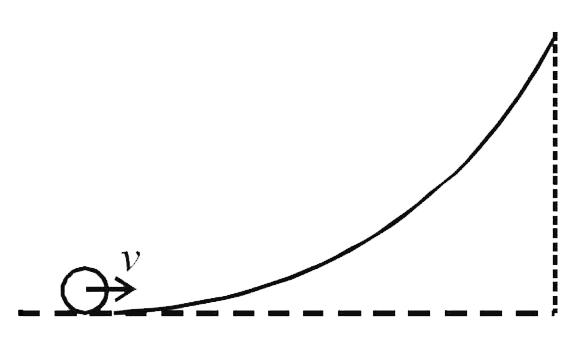
View SolutionA small mass attached to a string rotates on a frictionless table top as shown in Fig. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will

View SolutionAn autmobile moves on road with a speed of `54 km//h`. The radius of its wheel is `0.45 m` and the moment of inertia of the wheel about its axis of rotation is `3 kg m^(2)`. If the vehicle is brought to rest in `15 s`, the magnitude of average torque tansmitted by its brakes to the wheel is :
View SolutionThe moment of inertia of a uniform cylinder of length `l and radius R` about its perpendicular bisector is `I`. What is the ratio `l//R` such that the moment of inertia is minimum ?
View SolutionWhen a celling fan is switched off, its angualr velocity falls to half while it makes `36` rotations. How many more rotations will it make before coming to rest ?
View SolutionA point `P` moves in counter - clockwise direction on a circular path as shown in the figure . The movement of `P` is such that it sweeps out a length `s = t^(3) + 5 ` , where `s` is in metres and ` t` is in seconds . The radius of the path is `20 m` . The acceleration of `P` when ` t = 2 s` is nearly .
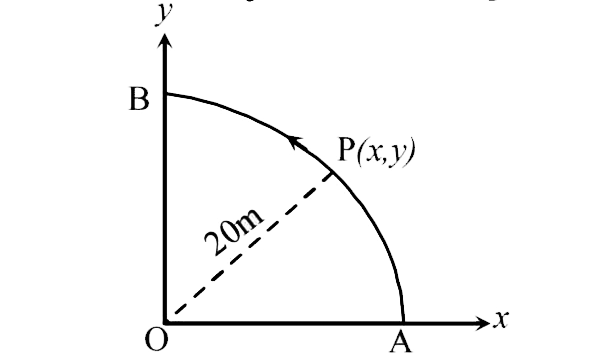
View SolutionA ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
View SolutionA wheel is subjected to uniform angular acceleration about its axis. Initially, its angular velocity is zero. In the first `2 sec`, it rotates through an angle `theta_(1)`, in the next `2 sec`, it rotates through an angle `theta_(2)`. The ratio of `theta_(2)//theta_(1)` is
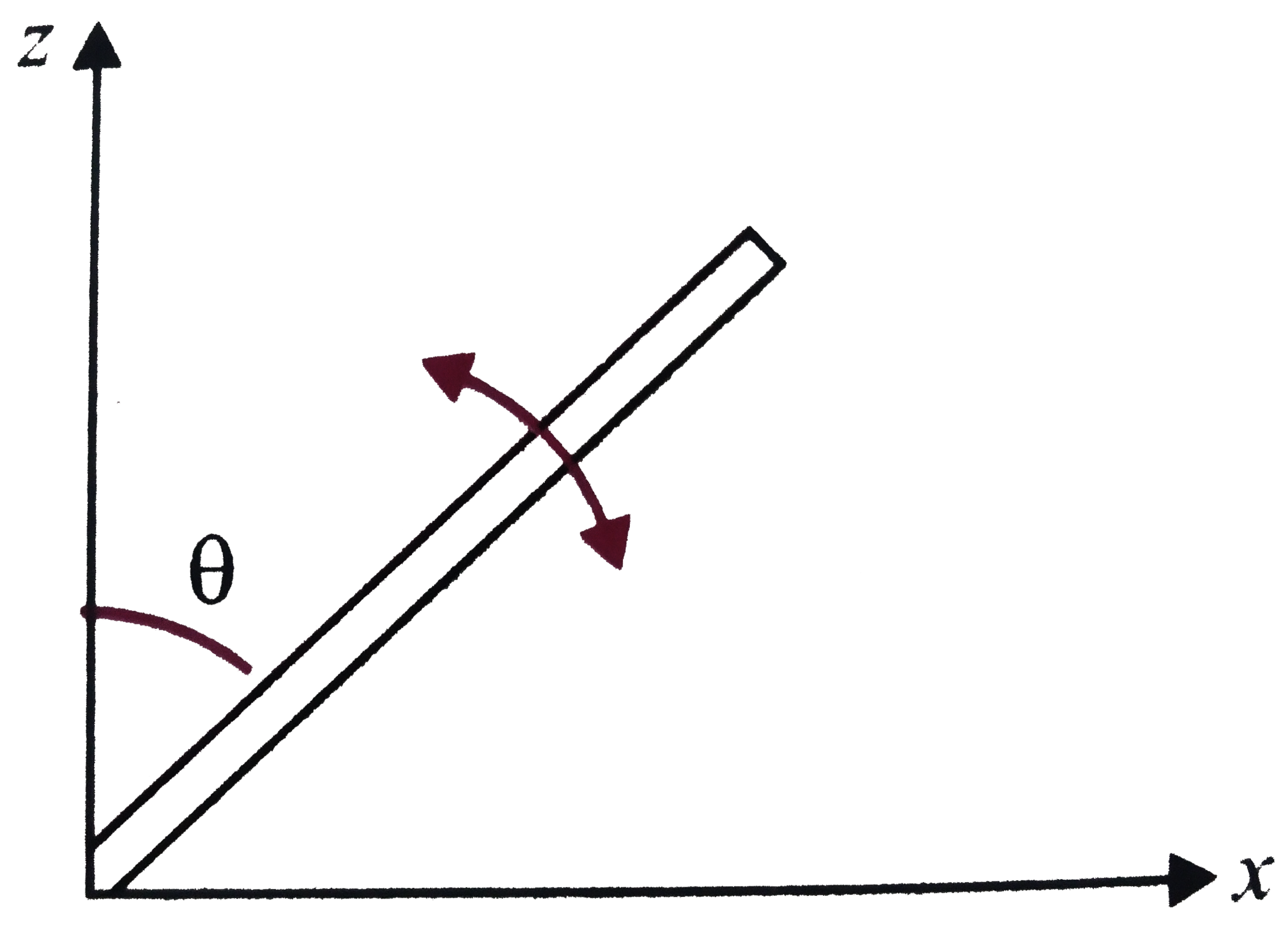
View SolutionA slender uniform rod of mass `M` and length `l` is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle `theta` with the vertical is
View SolutionThe ratio of the accelerations for a solid sphere (mass `m, and radius R`) rolling down an incline of angle `theta` without slipping, and slipping down the incline without rolling is
View SolutionA rod of length `L` is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, When it is in verticle position is
View SolutionA force `overset rarr(F) = alpha hati + 3 hatj + 6 hatk` is acting at a point `overset rarr(r ) = 2 hati - 6 hatj - 12 hatk`. The value of `alpha` for which angular momentum about origin is conserved is
View SolutionTwo stone of masses `m and 2 m` are whirled in horizontal circles, the heavier one in a radius `r//2` and the lighter one in radius `r`. The tangential speed of lighter stone is `n` times that of the value of heavier stone when thy experience same centripetal forces. the value of `n` is
View SolutionA uniform metallic rod rotates about its perpendicular bisector with constant angualr speed. If it is heated uniformly to raise its temperature slightly, then
View SolutionA unifrom disc is acted by two equal forces of magnitude `F`. One of them, acts tangentially to the disc, while other one is acting at the central point of the disc. The friction between disc surface and ground surface in `nF`. If `r` be the radius of the disc, then the value of `n` would be (in `N`)
View SolutionA massless rod S having length `2l` has equal point masses attached to its two ends as shown in figure. The rod is rotating about an axis passing through its centre and making angle `alpha` with the axis. The magnitude of change of momentum of rod i.e., `|(dL)/(dt)|` equals
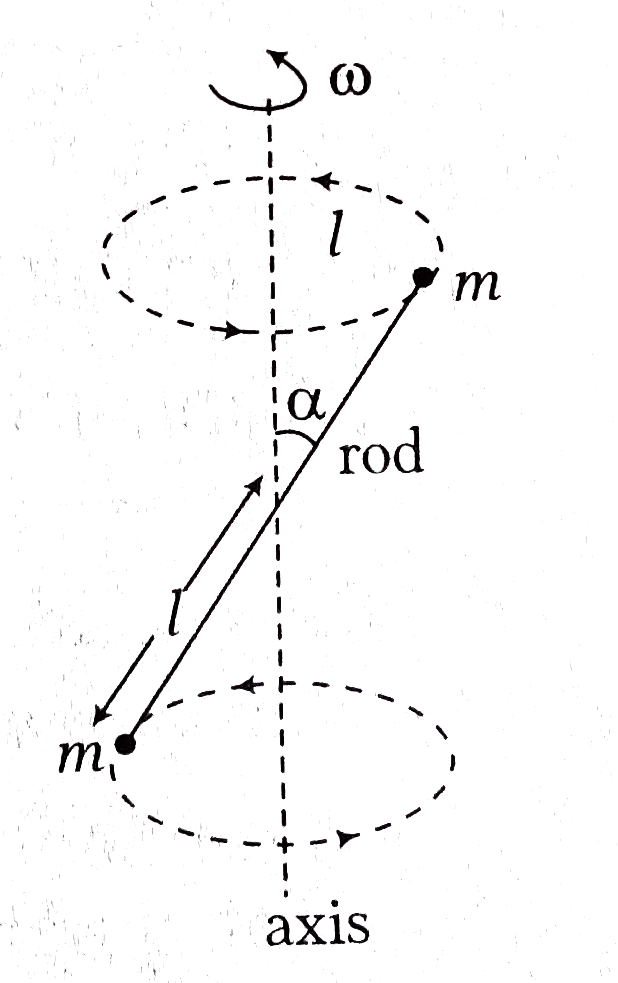
View SolutionA hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is `theta`, find the angular speed at which the bowl is rotating.
View SolutionA uniform circular disc of radius `50 cm` at rest is free to turn about an axis, which is perpendicular to the plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of `2.0 rad//s^(2)`. Its net acceleration in `m//s^(2)` at the end of `2.0 s` is approximately
View SolutionA uniform sphere of mass `500 g` rolls without slipping on a plane surface so that its centre moves at a speed of `0.02 m//s`.
The total kinetic energy of rolling sphere would be (in `J`)
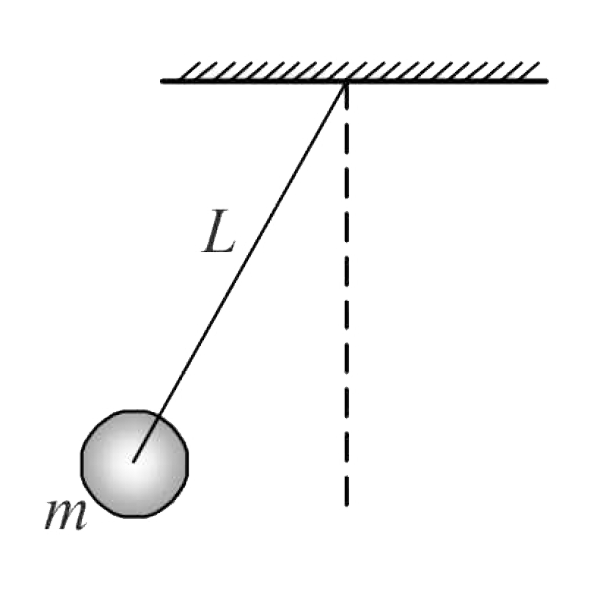
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed `omega` red/s about the vertical. About the point of suspension:
View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
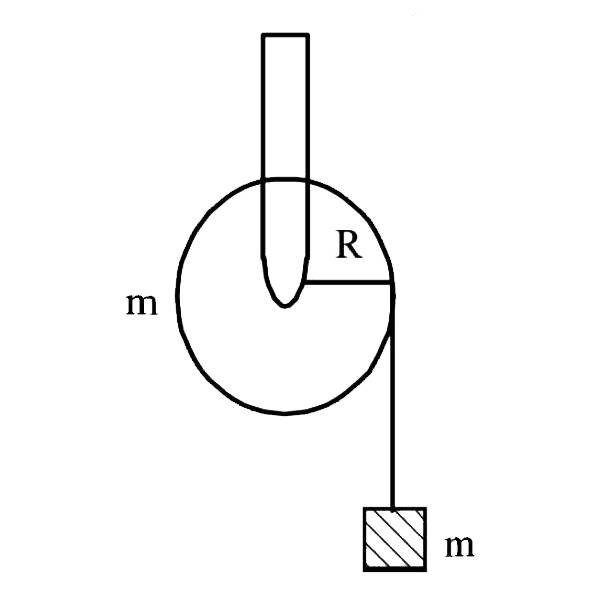
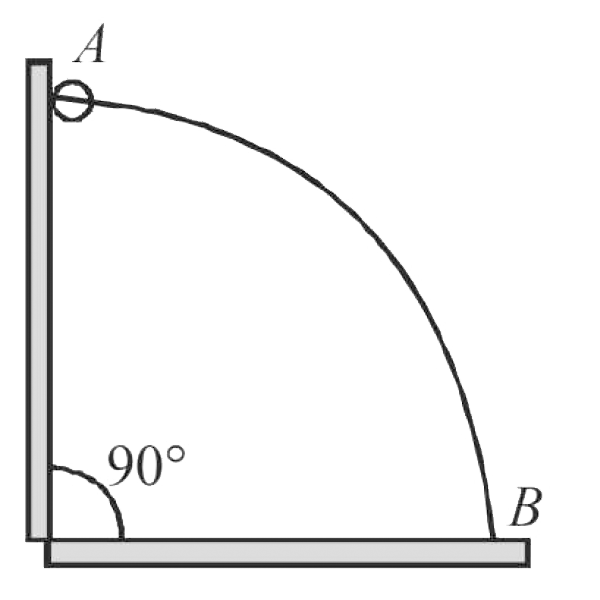
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
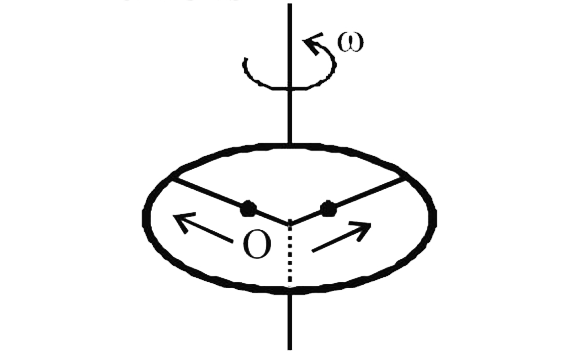
View SolutionA ring of mass M and radius R is rotating with angular speed `omega` about a fixed vertical axis passing through its centre O with two point masses each of mass `(M)/(8)` at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is `(8)/(9) omega` and one fo the masses is at a distance of `(3)/(5) R` from O. At this instant the distance of the other mass from O is
View SolutionA unifrom circular disc of radius `50 cm` at rest is free to turn about an axis, which is perependicular to the plane and passes through its centre. It is subjected to a torque which produces a constant angualr acceleration of `2.0 rad//s^(2)`. Its net acceleration in `m//s^(2)` at the end of `2.0 s` is approximately
View SolutionA paritcal of mass `10 g` moves along a circle of radius `6.4 cm` with a constant tangennitial acceleration. What is the magnitude of this acceleration . What is the magnitude of this acceleration if the kinetic energy of the partical becomes equal to `8 xx 10^(-4) J` by the end of the second revolution after the beginning of the motion?
View SolutionA particle of mass `m` is moving along the side of a square of side `a`, with a unifrom speed v in `XY` palne as shown in Fig. Which of the followig statements is false for the angualr momentum `overset rarr(L)` about the origin?
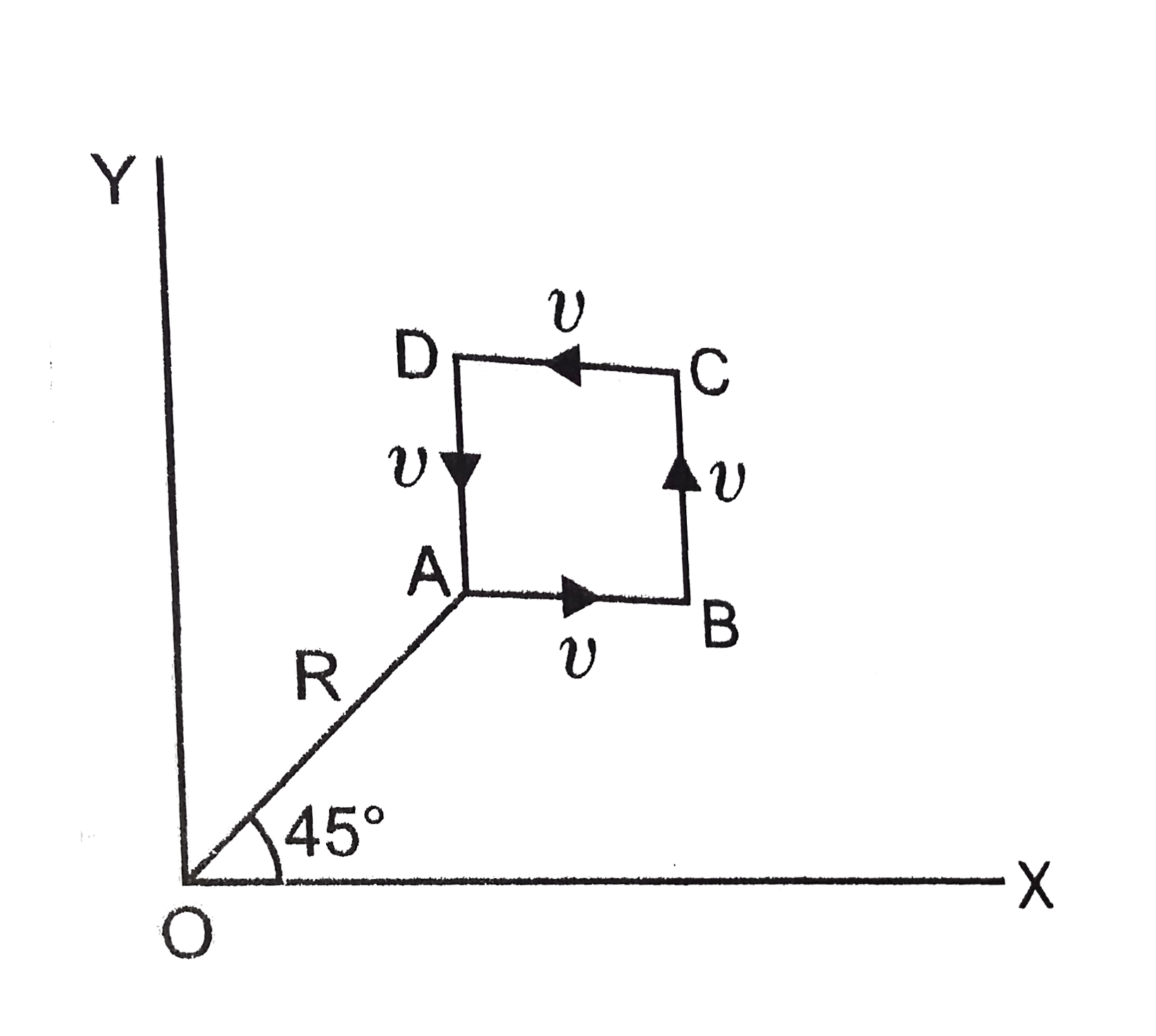
View SolutionA roller is made by joining together two cones at their vertices O, ti is kept on two rails AB and CD, which are placed asymmetrically with its axis perpendiuclar to CD and its center O at the centre of line joining AB and Cd it is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown As it moves, the roller wil tand to:
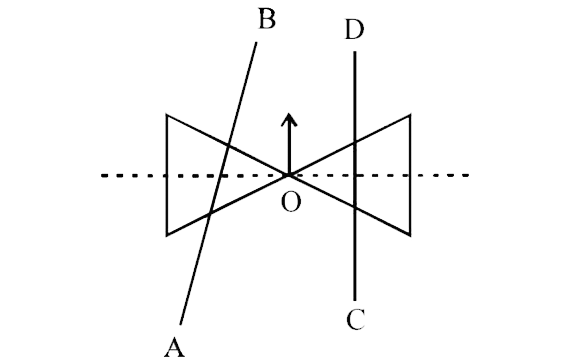
View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, h ltltR). The minimum increase in its orbital velocity required, So that the satellite could escape from the erth's gravitational field, is close to :(Neglect the effect of atomsphere.)
View SolutionA particle of mass `2 kg` located at the position `(hati + hatj)m` has velocity `2(hati - hatj + hatk) m//s` . Its angualr momentum about Z-axis in `kg m^(2)//s` is
View SolutionA wheel of radius `R` rolls on the ground with a unifrom velocity `v`. The velocity of topmost point releative to bottom must point is
View SolutionThe centre of a wheel rolling on a plaen surface moves with a speed `v_0`. A particle on the rim of the wheel at the same level as the centre will be moving at speed
View SolutionA disc and a solid sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
View SolutionA particle moves so that its position vertor is given by `overset rarr(r ) = cos omegat hatx + sin omegat haty`, where `omega` is a constant. Which of the following is true?
View SolutionA solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity `v m//s`. If it is to climb the inclined surface then `v` should be :
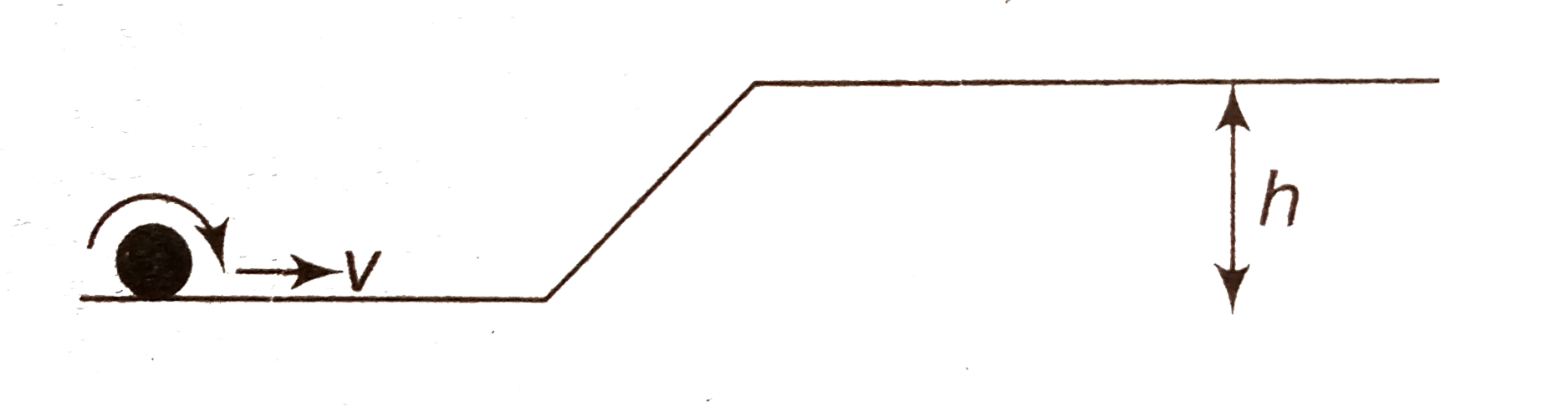
View SolutionA particle of mass `m = 5` unit is moving with a uniform speed `v = 3 sqrt(2)` unit `XY` plane aong the line `Y = X + 4`. The magnitude of the angular momentum about origin is
View SolutionA table fan rotating at a speed of `2400` rpm is switched off and the resulating variation of the revolution/minute time is shown in Fig. The total number of revolutions of the fan before it comes to rest is
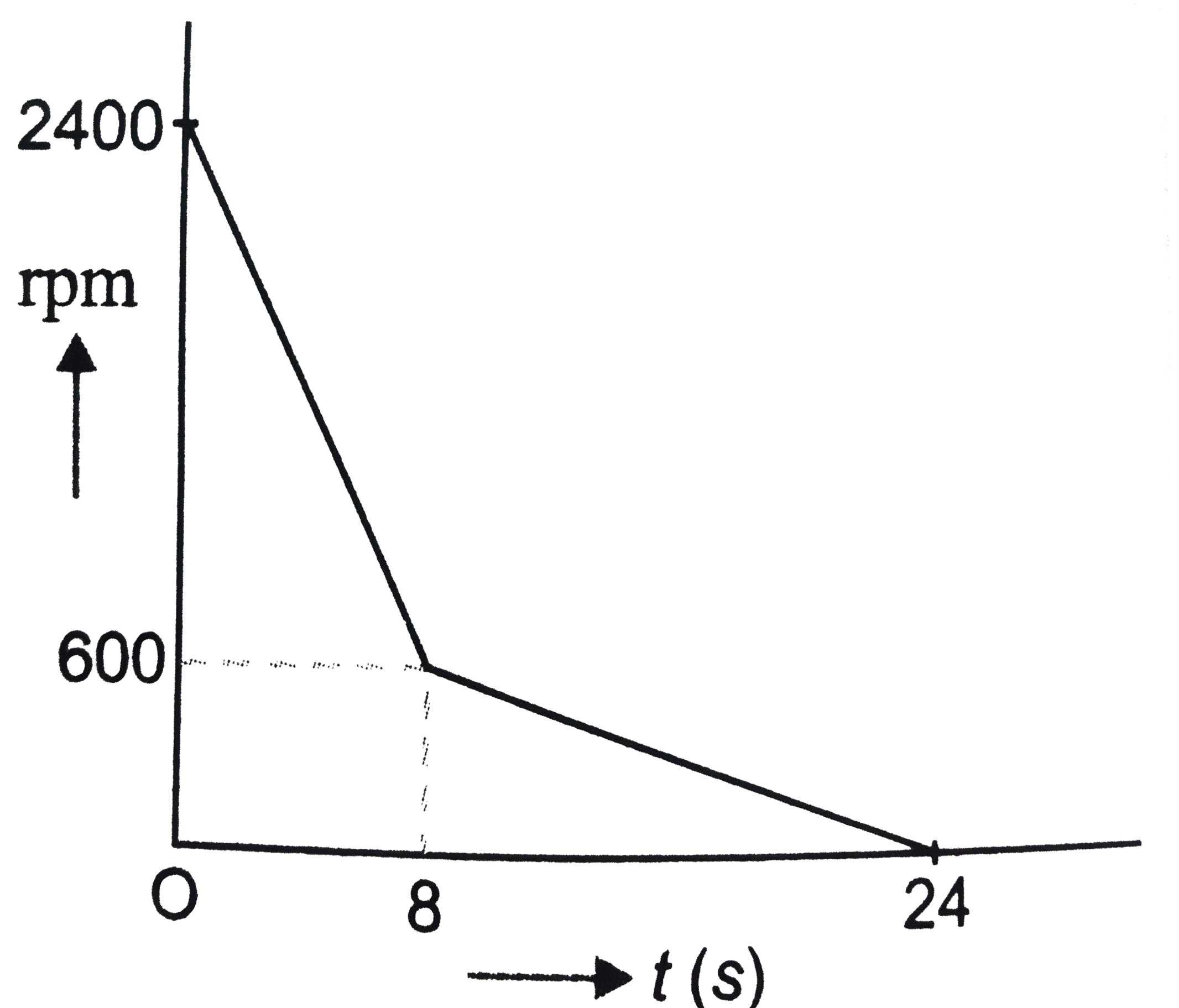
View SolutionA unifrom rod of length `l` and mass `m` is free to rotate in a vertical plane about `A` as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA wheel is subjected to uniform angualr acceleration about its axis. Initially, its angualr velocity is zero. In the first `2 sec`, it rotates through an angle `theta_(1)`, in the next `2 sec`, it rotates through an angle `theta_(2)`. The ratio of `theta_(2)//theta_(1)` is
View SolutionA sphere can roll on a surface inclined at an angle `theta` if the friction coefficient is more than `(2)/(7) g sin theta`. Suppose the friction coefficient is `(1)/(7) g sin theta`, and a sphere is released from rest on the incline,
View SolutionAngular momentum `L` is given by `L = P r` The variation of log `L` and `log P` is correctly shown in Fig.
View Solution`O` is the centre of an equilateral triangle `ABC`. `F_(1), F_(2)` and `F_(3)` are the three forces acting along the sides `AB, BC` and `AC` respectively. What should be the value of `F_(3)` so that the total torque about `O` is zero?
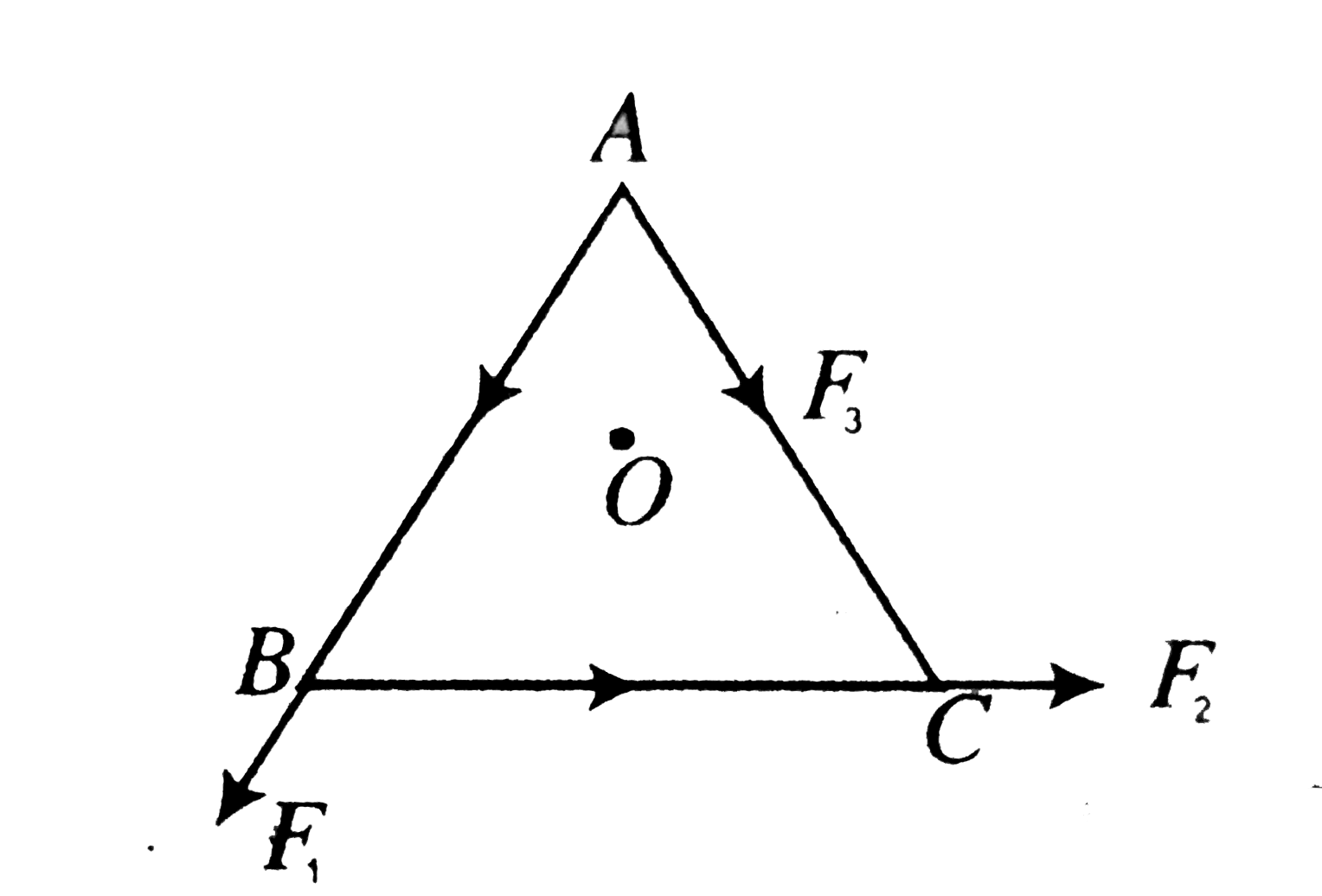
View SolutionA solid cylinder and a hollow cylinder, both of the same mass and same external fiameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which one will reach the bottom first ?
View SolutionA wheel has moment of inertia `5 xx 10^(-3) kg m^(2)` and is making `20 "rev" s^(-1)`. The torque needed to stop it in `10 s` is….. `xx 10^(-2) N-m`
View SolutionA wheel having moment of inertia `2 kg m^(2)` about its vertical axis, rotates at the rate of `60 rom` about this axis. The torque which can stop the wheel's rotation in one minuted woould be
View Solution
MULTIPLE CHOICE QUESTIONS questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion- Reason Type questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- FILL IN THE BLANKS
- Focus Multiple Choice Questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- Multiple Choice Questions Comprehension 2
- Multiple Choice Questions II.
- Multiple Choice Questions III. Comprehension 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- NCERT
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- QUESTIONS
- Sample problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.