Complete Solutions to PROBLEMS FOR PRACTICE of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP | PROBLEMS FOR PRACTICE |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
The centre of mass of three particles of masses `1 kg, 2kg and 3 kg` lies at the point `(3m, 3m, 3m)` where should a fourth particles of mass `4 kg` be positioned so that centre of mass of the four particle system at `(1m, 1m, 1m)`?
View SolutionThree point masses of `1 kg, 2kg and 3 kg` lie at `(1,2), (0,-1) and (2, -3)` respectively. Calculate the co-ordinates of the centre of mass of the system.
View SolutionTwo particle of mass `2 kg and 1 kg` are moving along the same straight line with speeds `2m//s and 5m//s` respectively. What is the speed of the centre of mass of the system if both the particles are moving (a) in same direction (b) in opposite direction ?
View SolutionFour particles `A, B, C and D` of masses `m, 2m, 3m and 4m` respectively are placed at corners of a square of side `x` as shown in Fig.

Locate the centre of mass.
View SolutionIf a man of mass `M` jumps to the ground from a height `h` and centre of mass moves a distance `x` in time taken by him to hit the ground, show that the average force acting on him is `Mgh//x`.
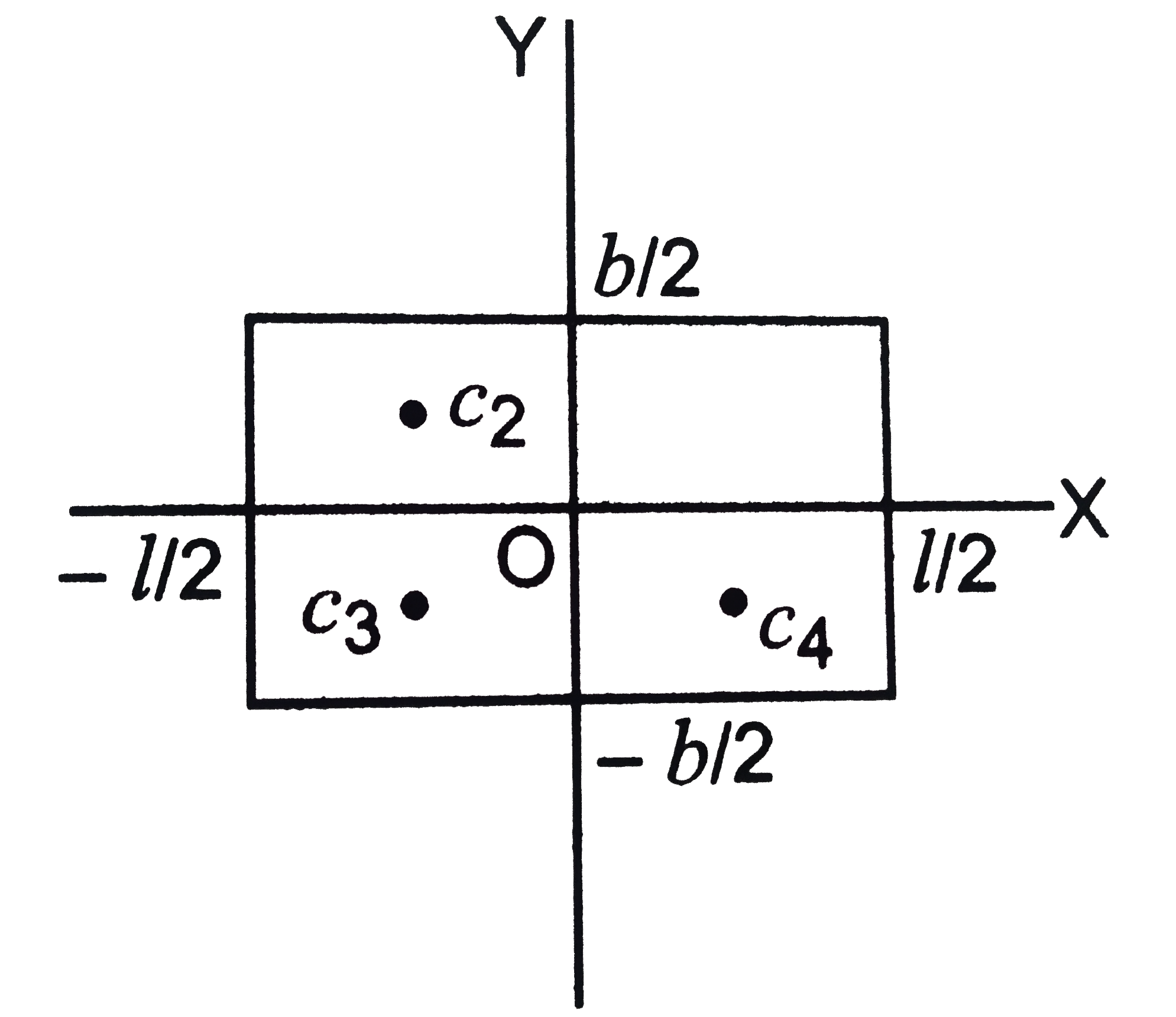
View SolutionFour particles of masses `m_(1) = 1 kg, m_(2) = 2 kg, m_(3) = 3 kg and m_(4) = 4 kg` are located at the corners of a rectangle as shown in Fig. Locate the position of centre of mass.
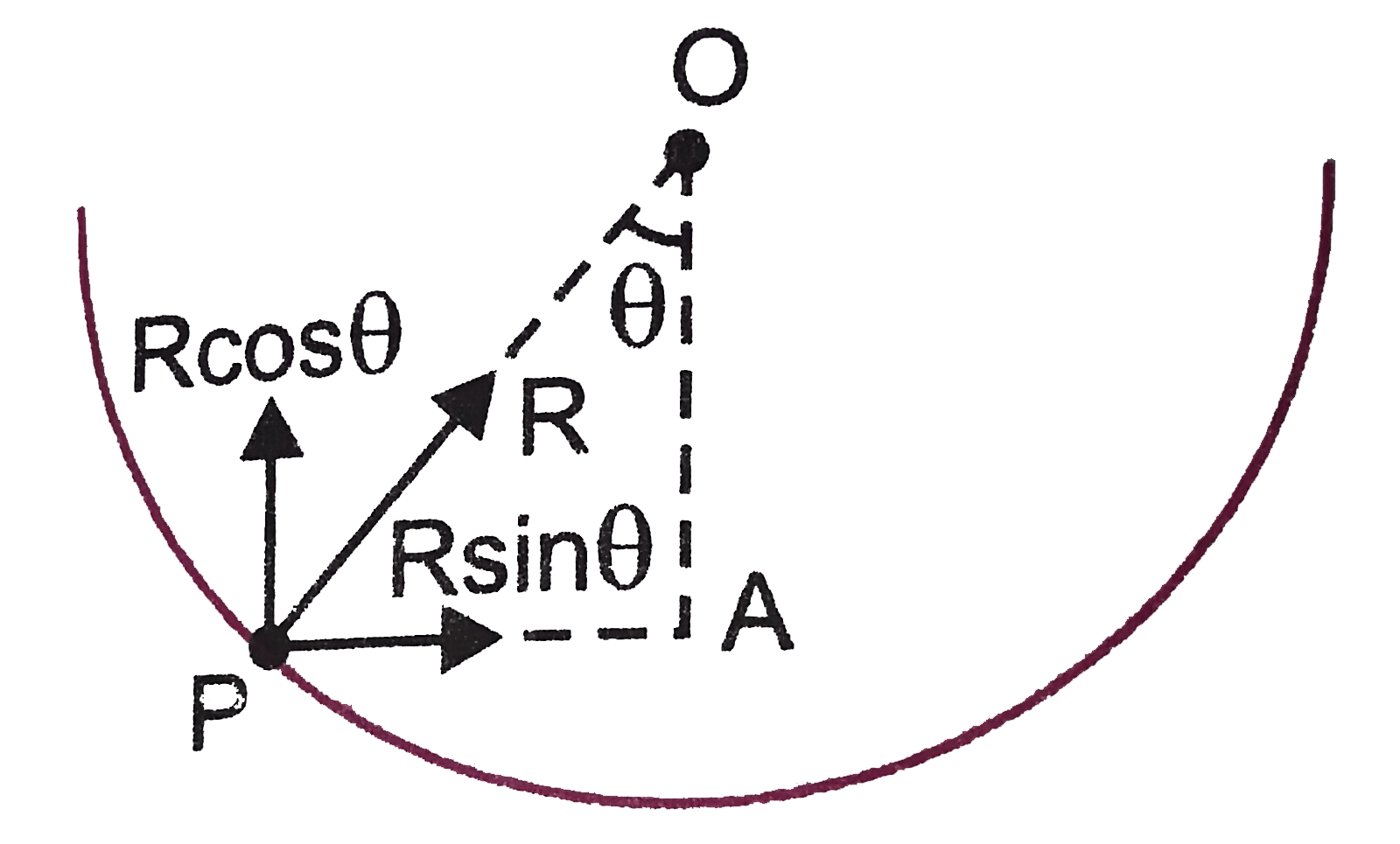
View SolutionTwo bodies of masses `10 kg and 2 kg` are moving with velocities `(2 hati - 7 hatj + 3hat k) and (-10 hati + 35 hatj - 3hatk) m//s` respectively. Calculate the velocity of their centre of mass.
View SolutionA square of side `4 m` having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre `O`.
View SolutionFrom a uniform circular disc of diameter `d,a` circular disc of diameter `d//6` and having centre at a distance `d//4` from the centre of the disc is scooped out. Determine the centre of mass of remaining portion.
View SolutionA rectangular plate of dimensions `l xx b` is in `x -y` plane as shown in Fig. If the portion of this plate lying in quadrant `I` is removed, find the position of centre of mass of remaining part of plate.
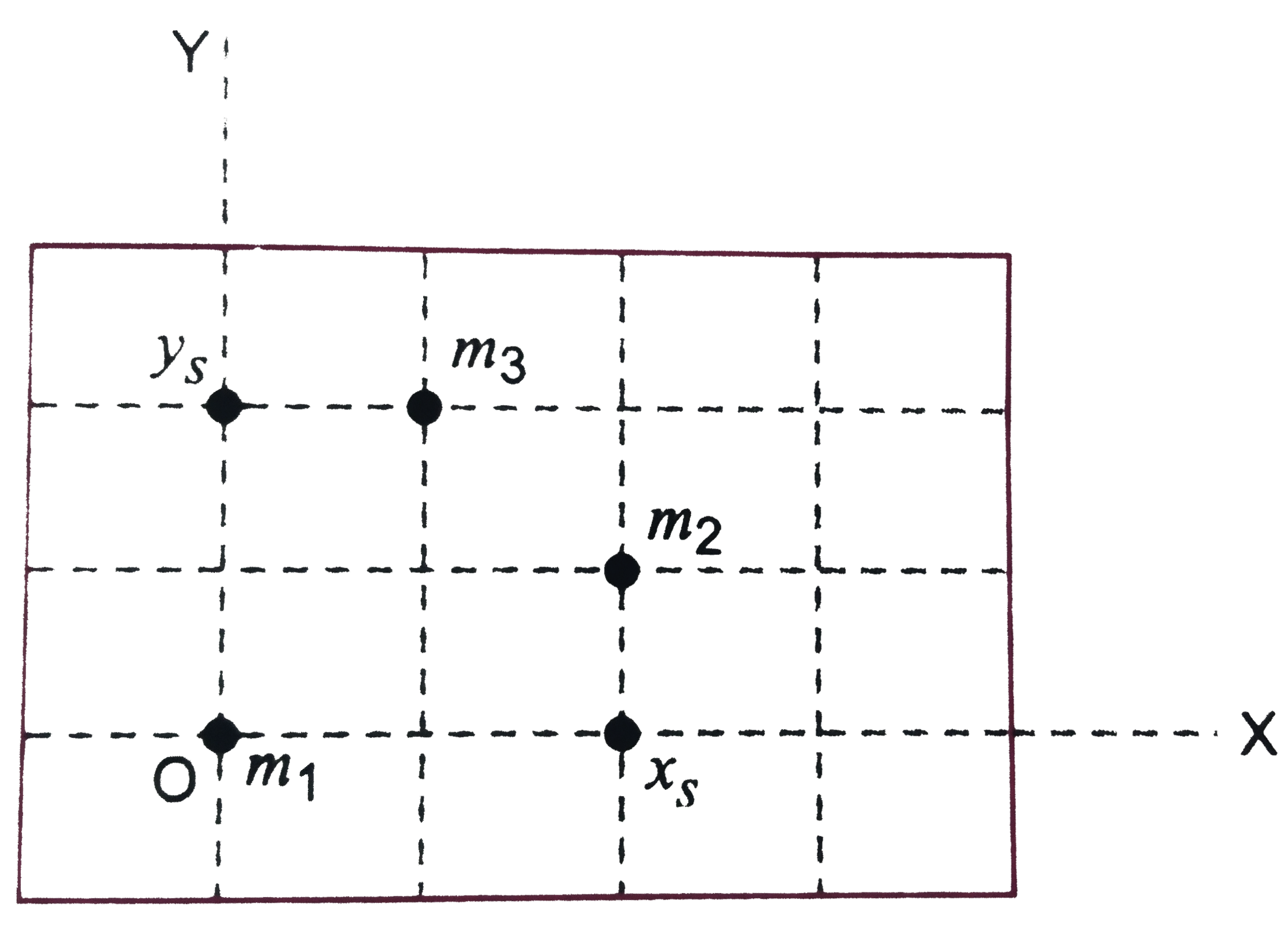
View SolutionFig. shown a three particle system with masses `m_(1) = 3.0 kg, m_(2) = 4.0kg` and `m_(3) = 8.0 kg`. The scales on the axes are set by `x_(s) = 2.0 m` and `y_(s) = 2.0m`. What are the co-ordinates of centre if mass ? If `m_(3)` is gradually increased, does the centre of mass of the system shift towards or away from that particle or does it remain stationary ?
View SolutionA flywheel of mass `25 kg` has a radius of `0.2 m`. It is making 240 rpm. What is the torque necessary to bring it to rest in `20 s` ? If the torque is due to a force applies tangentially on the rim of the wheel, what is the magnitude of the force ? Assume that mass of flywheel is concentrated at its rim.
View SolutionA rope is wound round a hollow cylinder of mass `3 kg and radius 40 cm`. If the rope is pulled with a force of `30 N`, what is the angualr acceleration of the cylinder ?
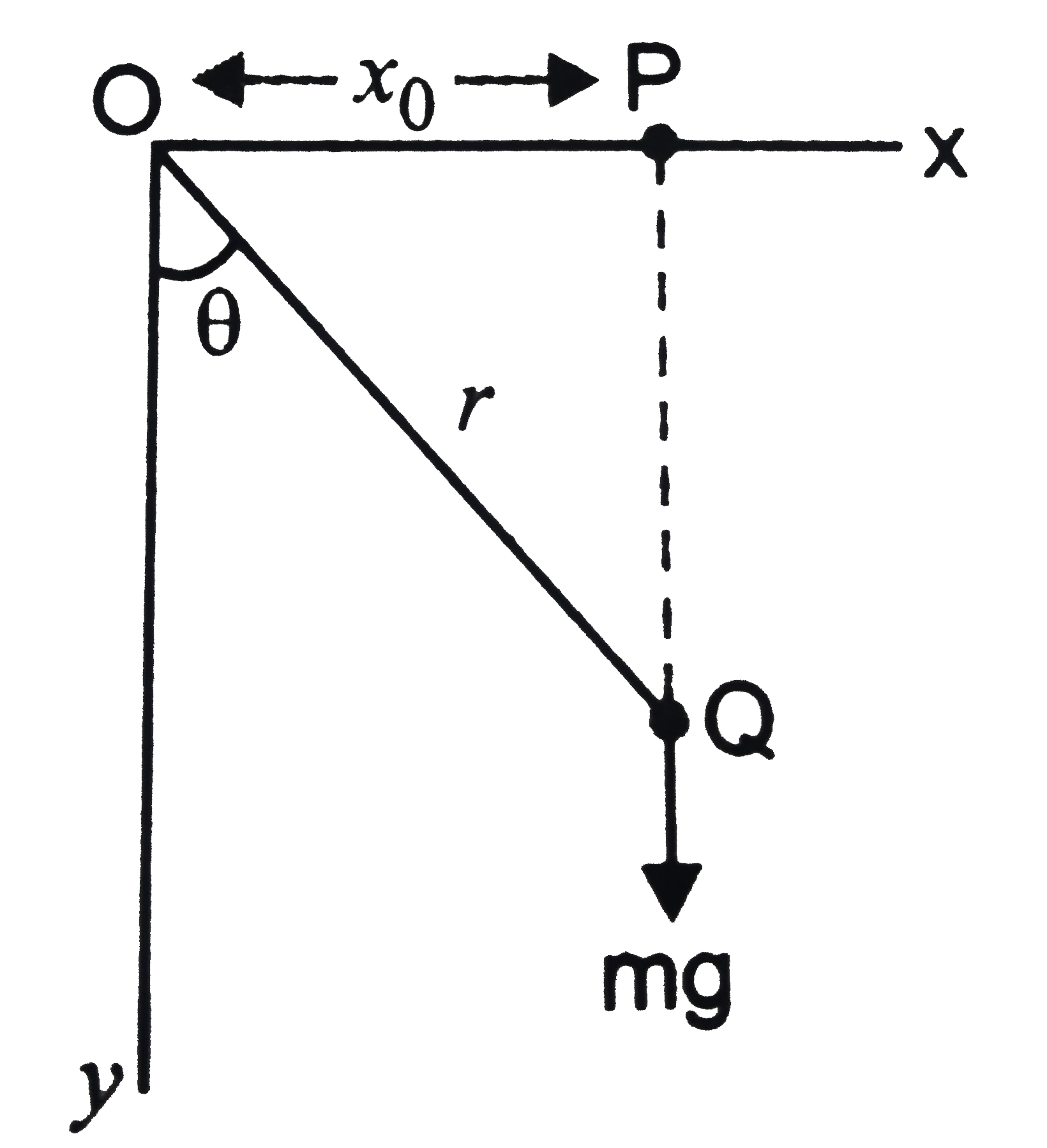
View SolutionA particle of mass `m` is released from rest from point `P` at `x = x_(0)` on X-axis from origin `O` and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time `t`, when it is at the point `Q w.r.t.O` ?
View SolutionA unifrom circular disc of mass `200g` and radius `4 cm` is rotated about one of its diameters at an angular speed of `10 rad//s`. Find its abgular momentum about the axis of rotation ?
View SolutionDetermine the angular momentum of a car of mass `200 kg` moving in a circular track of diameter `100 m` with a speed of `40 m//s`.
View SolutionAn electron revolves around the nucleus of an atom in a circular orbit of radius `4 Å` with a speed of `6.0 xx 10^(6) m//s`. If mass of electron is `9.0 xx 10^(-31) kg`, what is its angular momentum ?
View SolutionSuppose earth is a point mass of `6 xx 10^(24) kg` revolving around the sun in a circular orbit of diameter `3xx10^(8) km` in time `3.14 xx 10^(7) s`. What is the angular momentum of the eart around the sun ?
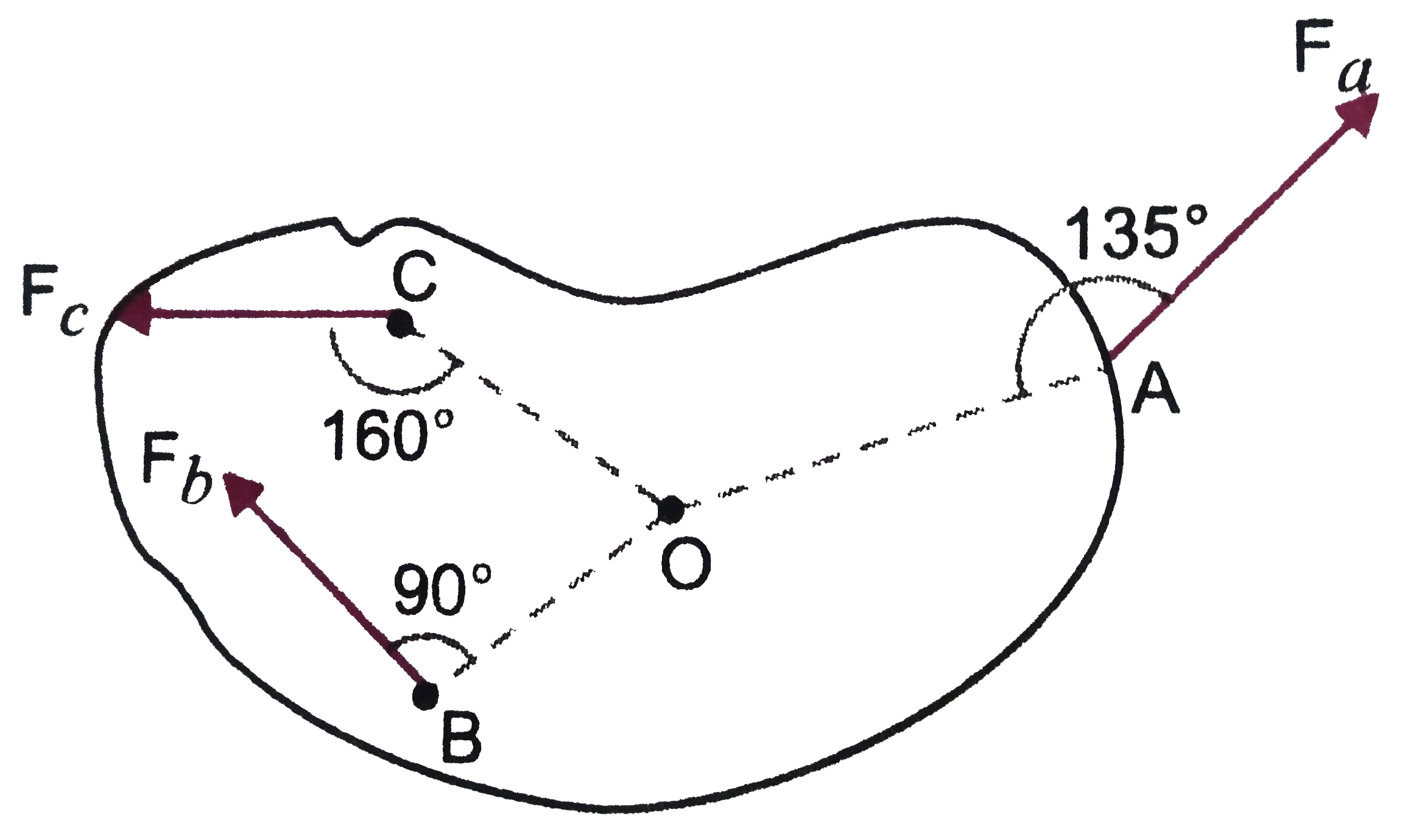
View SolutionThe body shown in Fig. is pivoted at point `O`. Three forces act on it `F_(a) = 10N` at point `A, 8.0 m` from `O, F_(b) = 16 N` at` B, 4.0m` from O, and `F_(c) = 19 N` at `C, 3.0 m` from `O`. What is the net torque about `O`.
View SolutionThe speed of a wheel increases from `600 `rpm to 1200 rpm in `20 s`. What is its angular acceleration ? How many revolutions will it make during this time ?
View SolutionA flywheel rotating at `420` rpm slows sown at a constant rate `2 rad s^(-2)`. What time is required to stop the flywheel ?
View SolutionThe spin drier of a washing machine revolving at`15 rps` slows down to `5 rps`, while making `50` revolutions. Find (a) angular acceleration and (b) time taken.
View SolutionOn applying a consatnt torque, a wheel at rest, turns through `400` radian in `10 s`. Find angular acceleration. If same torque continues to act, what will be angular veclocity of the wheel after `20 s` from stars ?
View SolutionA cord is wound around the circumference of a bicycle wheel (without tyre) of diameter `1 m`. A mass of `2 kg` is tied at the end of the cord and it is allowed to fall from rest. The weight falls `2 m` in `4 s`. The axle of the wheel is horizontal and the wheel rotates which its plane vertical. if `g = 10 ms^(-2)`, what is the angular acceleration of the wheel ?
View SolutionA car is moving at a speed of `72 km//h`. The diamter of its whells is `0.5 m`. If the wheels are stopped in `20` rotations by applying brakes, calcualte the angular retardation produced by the brakes.
View SolutionAn autmobile travelling at `80 km//h` has tyres of `75.0 cm` diameter. What is the angualr speed of the tyres about their axles ? If the car is brought to stop uniformly in `30` complete turns of the tyres without skidding, what is the magnitude of angular acceleration of the wheels ? How far does the car move during the braking ?
View SolutionA wheel rotating at an angular speed of 20 rad/s ils brought to rest by a constant trouque in 4.0 secons. If the moiment of inertia of the wheel about the axis of rotation is 0.20 `kg-m^2` find the work done by the torque in the first two seconds.
View SolutionThe centre of gravity of a loaded texi is `1.5 m` above the ground, and the distance between the wheels is `2m`. What is the maximum speed with which it can go round an unbanked curve of radius `100 m` without being turned upside down. What minimum value of coefficient of friction is needed at this speed ?
View SolutionCalculate rotational `K.E.` of earth about its own axis, taking it to be a sphere of mass `6 xx 10^(24) kg` and radius `6400 km`.
View SolutionA wheel of mass `5 kg` and radius `0.40 m` is rolling on a road without sliding with angular velocity `10 rad s^-1`. The moment of ineria of the wheel about the axis of rotation is `0.65 kg m^2`. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
View SolutionA thin metal hoop of radius `0.25 m` and mass `2 kg` stars from rest and rolls down an inclined plane. If its linear velocity on reaching the foot of the plane is `2 m//s`, what is its rotational `KE` at that instant ?
View SolutionA circular disc of mass `M` and radius `r` is set rolling on a table. If `omega` be its angular velocity, show that its total `K.E.` is given by `(3//4)M v^(2), where v` is its linear velocity `M.I.` of circular disc `= (1//2) mass xx (radius)^(2)`.
View SolutionA spherical ball rolls on a table without slipping. Determine the percentage of its `K.E.` which is rotational. Moment of inertia of sphere `= (2//5) xx mass xx ("radius")^(2)`.
View SolutionA solid cylinder rolls down an inclined plane. Its mass is `2 kg and radius 0.1 m`. It the height of the inclined plane is `4m`, what is its rotational `K.E.` when it reaches foot of the plane ? Assume that the surfaces are smooth. Take `M.I.` of solid cylinder about its axis = `mr^(2)//2`.
View SolutionThe earth has a mass of `6 xx 10^(24) kg` and a radius of `6.4 xx 10^(6)m`. Calculate the amount of work that must be done to slow down its rotation so that duration of day becomes `30` hrs instead of 24 hours.
Moment of inertia of earth `= (2)/(5)MR^(2)`.
View SolutionA bucket of mass `8 kg` is supported by a light rope wound around a solid wooden cylinder of mass `12 kg and radius 20 cm`, free to rotate about its axis. A man holding the free end of the rope with the bucket and the cylinder at rest initially, lets go the bucket freely downward in a well `50 m` deep. Neglecting friction, obtain the speed of bucket and angualr speed of the cylinder just before the bucket enters water. Take `g = 10 m//s^(2)`.
View SolutionA hoop of radius `2 m` weight `100 kg`.It rolls along a horizontal floor so that its centre of mass has a speed of `20 cm s^-1`. How much work has to be done to stop it ?
View SolutionIf a constant torque of `500 N-m` turns a wheel of moment of inertia `100 kg m^(2)` about an axis passing through its centre, find the gain in angular velocity in `2 s`.
View SolutionA ring of diameter `0.4 m` and of mass `10 kg` is rotating about its axis at the rate of 2100 rpm. Calculate moment of inertia, angular momentum and rotational `KE` of the ring.
View SolutionA cylinder of length `20 cm` and radius `10 cm` is rotating about its central axis at an angular speed of `100 rad//s`. What tangential force will stop the cylinder at a unifrom rate is `10 s` ? Given moment of inertia of the cylinder about its axis of rotation is `8.0 kg m^(2)`.
View SolutionA `40 kg` flywheel in the from of a unifrom circular disc `200 cm`. in diameter is making `120` revolutions/minute. Calculate angular momentum. Moment of inertia of disc `= (1//2) mass xx ("radius")^(2)`.
View SolutionA circular ring of diameter `40 cm` and mass `1 kg` is rotating about an axis normal to its plane and passing through the centre with a frequency of `10 rps`. Calculate the angular momentum about the axis of rotation.
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A stirng is wrapped over its rim and is ulle dby a force of 5.0 N. It is found that the torque roduces an angular acceleration 2.0 `rad/s^2` in the wheel. Calculate the moment of inertia of the wheel.

View SolutionA force of `36N` is applied to a particle located at `0.15 m` from the axis of rotation. What is the magnitude of the torque about this axis, if the angle between the direction of the applied force and radius vector is (a)`120^(@) (b) 45^(@)`?
View SolutionA circular ring of diameter `40 cm` and mass `1 kg` is rotating about an axis normal to its plane and passing through the centre with a frequency of `10 rps`. Calculate the angular momentum about the axis of rotation.
View SolutionA torque of `10^(8)` dyne - cm is applied to a fly wheel of mass `10 kg` and radius of gyration `50 cm`. What is the resultant angular acceleration ?
View SolutionA sphere of mass `2 kg` and radius `5 cm` is rotating at the rate of `300` revolutions per minute. Calculate the torque required to stop it in `6.28` revolutions. [Moment of inertia of sphere about diameter `= 2//5 mass xx ("radius")^(2)]`.
View SolutionA flywheel of moment of inertia 5.0 `kg-m^2` is rotated at a speed of 60 rad/s. Because of the friction at the axle, it comes to rest in 5.0 minutes. Find a. The average torque of the friction. B. the total work done by the friction and c. the angular momentum of the wheel 1 minute before it stops rotating.
View SolutionHow much tangential force will be needed to stop the earth in one year, if it is rotating with an angular velocity of `7.3 xx 10^(-5) rad//s` ? Given moment of inertia of earth `= 9.3 xx 10^(37) kg m^(2)` and radius of earth `= 6.4 xx 10^(6) m`.
View SolutionA boy is seated in a revolving chair revolving at an angular speed of 120 rpm. By some arrangement, the boy decrease the moment of inertia of the system from `6 kg m^(2)` to `2 kg m^(2)`. What will be the new angular speed ?
View SolutionIf the earth expands suddenly to twice its diamteter, what would be the length of the day ?
View SolutionProve that for an earth satellite, the ratio of its velocity at apogee (when farthest from earth) to its velocity at perigee (when closer to earth) is in the inverse ratio of its distance at apogee and perigee.
View SolutionA uniform disc rotating freely about a vertical axis makes `90` rpm. A small piece of wax of mass `m` gram falls vertically on the disc and sticks to it at a distance `r cm` from the axis. If number of rotations per minute reduces to `60`, find the moment of inertia of the disc.
View SolutionA circular disc of moment of inertia `I_(t)` is rotating in a horizontal plane about its symmetry axis with a constant angular velocity `omega_(i)`. Another disc of moment of inertia `I_(b)` is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed `omega_(f)`. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA disc of mass `M` and radius `r` is rotating with an angular velocity `omega`. If gently, two masses `m` each are placed at a distance `r//2` on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionCalculate moment of inertia of a uniform circular disc of mass `700 g` and diameter `20 cm` about
(i) an axis through the centre of disc and perpendicular to its plane, (ii) a diameter of disc, (iii) a tangent in the plane of the disc, (iv) a tangent perpendicular to the plane of the disc.
View SolutionWhat is the moment of inertia of a ring of mass `2 kg` and diameter `1 m` about a transverse axis passing through its centre. How is moment of inertia affected if axis passes through edge of the ring parallel to given axis ?
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionFind the radius of gyrational and moment of inertia of a rod of mass `100g` and length `1 m` about an axis passing through its centre and perpendicular to its length.
View SolutionFour particles of masses `4 kg, 2 kg, 3kg and 5 kg` are respectively located at the four corners `A, B, C, D` of a square of side `1 m`. Calculate the moment of inertia of the system about
(i) the axis passing through point of intersection of the diagonals and perpendicualr to the plane of the square. (ii) side `AB` (ii) diagonal `BD`.
View SolutionCalculate the moment of inertia of a circular disc of radius `10 cm`, thickness `5 mm` and uniform density `8 g cm^(-3)`, about a transverse axis through the centre of the disc.
View SolutionThe earth has a mass of `6 xx 10^(24) kg` and a radius of `6.4 xx 10^(6)m`. Calcualte the amount of work that must be done to slow down its rotation so that duration of day becomes `30` hrs instead of 24 hours.
Moment of inertia of earth `= (2)/(5)MR^(2)`.
View SolutionA uniform rod of length 1 metre has a mass of `500 gram`. What is moment of inertia of the rod about an axis passing through the centre of the rod perpendicular to its length. How is moment of inertia changed when the same axis passes through one end of the rod ?
View SolutionThe wheel of a motor, accelerated uniformly from rest, rotates through 2.5 radian during the first second. Find the angle rotated during the next second.
View SolutionA rod of length `l` whose lower end is fixed along the horizontal plane starts from the vertical position. The velocity of the upper end of the rod when it hits the ground is
View SolutionA uniform rod of length `1m` having mass `1 kg` rests against a smooth wall at an angle of `30^(@)` with the ground. Calculate the force exerted by the ground on the rod. Take `g = 10 ms^(-2)`.
View SolutionTwo small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed `omega`. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionA cylinder of mass `5 kg` and radius `30 cm` is rolling down an inclined plane at an angle of `45^(@)` with the horizontal. Calculate (i) force of friction (ii) acceleration of cylinder (iii) minimum value of coeff. of static friction so that cylinder does not slip while rolling down the plane.
View SolutionA wheel of radius `6 cm` is mounted so as to rotate about a horizontal axis through its centre. A string of negligibe mass wrapped round its circumference carries a mass of `0.2 kg` attrached to its free end. When let fall, the mass descends through `1 m` in `5 s`. Calculate the angular acceleration of the wheel, its moment of inertia and tension in the cord.
View Solution
PROBLEMS FOR PRACTICE questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion- Reason Type questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- FILL IN THE BLANKS
- Focus Multiple Choice Questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- Multiple Choice Questions Comprehension 2
- Multiple Choice Questions II.
- Multiple Choice Questions III. Comprehension 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- NCERT
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- QUESTIONS
- Sample problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.