Complete Solutions to ADVANCED PROBLEMS FOR COMPETITIONS of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP | ADVANCED PROBLEMS FOR COMPETITIONS |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
A `70kg` man stands in contact against the inner wall of a hollow cylindrical drum of radius `3m` rotating about its verticle axis. The coefficient of friction between the wall and his clothing is `0.15` . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA solid cylinder at rest at top of an inclined plane of height `2.7 m` rolls down without slipping. If the same cylinder has to slide down a frictionaly inclined plane and acquires the same velocity as that acquired by centre of mass of rolling cylinder at the bottom of the incline, what should be the height of inclined plane ?
View SolutionFind the maximum speed at which a car can turn round a curve of `30 m` radius on a level road if coefficient of friction between the tyress and road is `0.4. Take g = 10 m//s^(2)`.
View SolutionA tube of length L is filled completely with an incomeressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity `omega.` The force exerted by the liquid at the other end is
View SolutionA particle describes a horizontal circule on the smooth inner surface of a coincal funnel as shown in Fig. If the height of the plane of the circle above the vertex is `9.8 cm`, find the speed of the particle.
View SolutionA uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to `L`. Locate the position of centre of mass of the system w.r.t. the centre of the square.
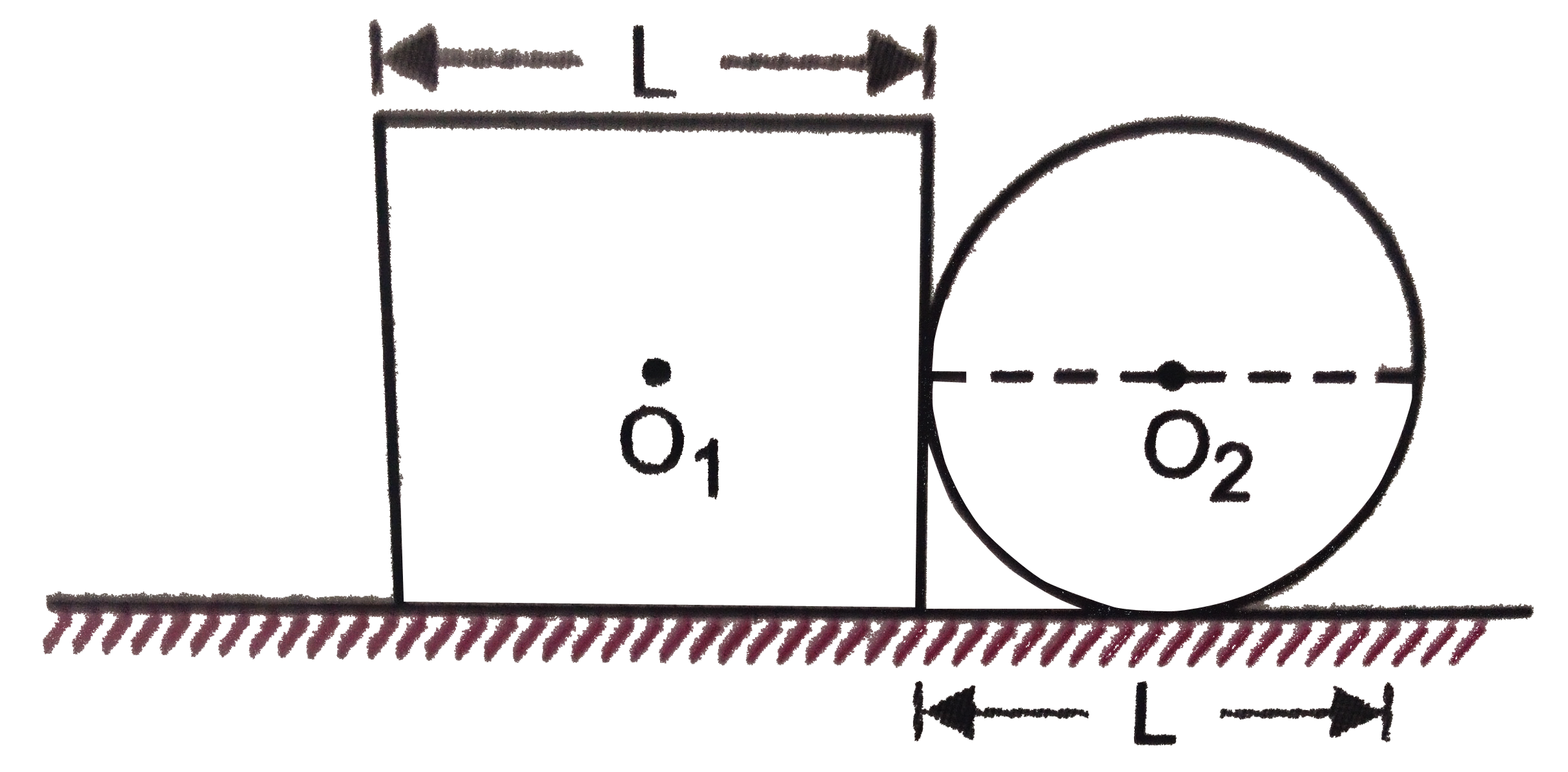
View SolutionFind the centre of mass of a uniform semicircular ring of radius `R` and mass `M`.
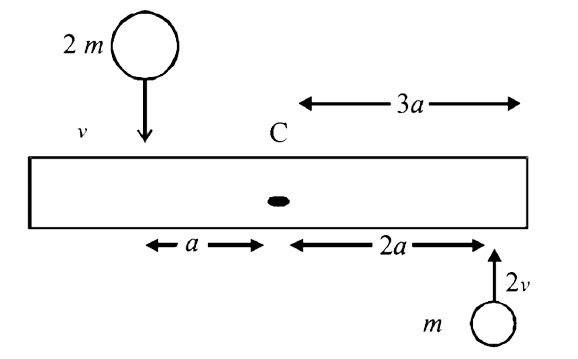
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by `omega`, E and `v_c` respecitvely, we have after collison
View SolutionHalf of the recrtangular plate shown in figure is made of a material of density `rho_1` and the other half of density `rho_2`. The length of the plate is L. Locate the centre of mass of the plate.

View SolutionFind the location of centre of mass of a uniform semicirular plate of radius `R` and mass `M`.
View SolutionThe density of a linear rod of length L varies as `rho=A+Bx` where x is the distance from the left end. Locate the centre of mass.

View SolutionA cubical block of ice of maas m and edge L is placed in a large tray of maas M. If the ie melts, how far does the centre of maas of the system ''ice plus tray'' come down?
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 `kg-m^2` nd radius 20 cm. The wheel is free to rotate about it axis. Initially, thewheel is t rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA wheel of rdius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination `theta` as shownin figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. INitialy, tehwheel is rotating at a speed `omega` in direction such that the block slides pu the plane. How far wil the block move before stopping?

View SolutionA solid sphere of mass `3 kg` and radius `2m` is free to rotate about an axis passing through its centre. Find a constant tangential force `F` required to rotate the sphere with a velocity of `10 rad//s` in `2 sec`. Starting from rest. Also, find the number of rotations made by the sphere in that time interval.
View SolutionTwo discs of radii `R and 2R` are pressed against eachother. Initially, disc wit radius `R` is rotating with angular velocity `omega` and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is `I` and of bigger disc is `2I` about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
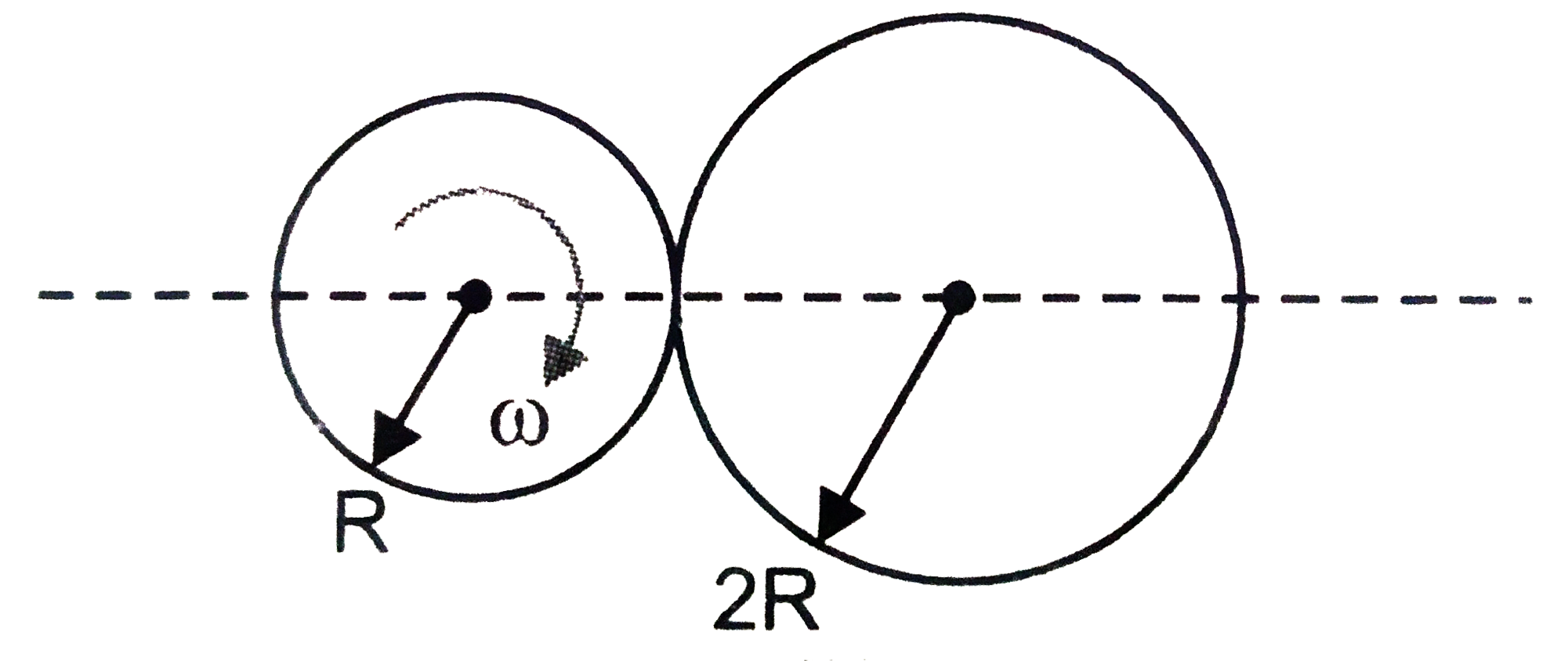
View Solution
A solid ball rolls down a parabolic path ABC from a height h as shown in figure. Portion AB of the path is rough while BC is smooth. How high will the ball climb in BC?
View SolutionA cylinder of mass `2kg` and radius `10cm` is held between two planks as shown in Fig. Calculate `KE` of the cylinder when there is no slipping at any point.

View SolutionA rod of mass `m` and length `l` is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View Solution
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance `h` above the centre line as shown in figure. The ball leaves the cue with a speed `v_(0)` and because of its backward slipping eventually acquires a final
speed `(9)/(7)v_(0)` show that `h=(4)/(5)R`
Where `R` is the radius of the ball.
View Solution
ADVANCED PROBLEMS FOR COMPETITIONS questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion- Reason Type questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- FILL IN THE BLANKS
- Focus Multiple Choice Questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- Multiple Choice Questions Comprehension 2
- Multiple Choice Questions II.
- Multiple Choice Questions III. Comprehension 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- NCERT
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- QUESTIONS
- Sample problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.