Complete Solutions to SOLVED EXAMPLES of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| PRADEEP | SOLVED EXAMPLES |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
Find the centre of mass of a uniform triangula lamina.
View SolutionFind the centre of mass of three particle at the vertices of an equilateral triangle. The masses of the particle are `100g, 150 g, and 200g` respectively. Each side of the equilateral triangle is `0.5m` along.
View SolutionFind the centre of mass of a uniform `L` shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is `3kg`.

View SolutionFind the position of centre of mass of the T-shaped plate from `O`, in Fig.

View SolutionFrom a uniform circular disc of radius `R`, a circular disc of radius `R//6` and having centre at a distance `R//2` from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA circular plate of uniform thickness has a diameter fo 56cm. A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.

View SolutionDetermine the coordinates of the centre of mass of a right circular soild cone of base radius `R` and height `h`.
View SolutionA uniform thin rod of length `3 L` is bent at right angles at a distance `L` from one end as shown in Fig. If length of rod is `1.8m`, find the co-ordinates and position vector of the mass of the system.

View SolutionA man of mass `m_(1)` is standing on a platform of mass `m_(2)` kept on a smooth horizontal surface. If the man moves a distance `d` w.r.t., the platform, find the displacement of the platform w.r.t., ground.
View SolutionA torque of `10^(3) N-m` acting on a rigid body, turns it throughr `30^(@)` in `0.2` second. Calculate work done by the body and power of torque.
View SolutionA constant torque is acting on a wheel. If starting from rest, the wheel makes n rotations in t seconds, show that the angular
acceleration is given by `alpha = (4pi n)/(t^(2)) rad s^(-2)`.
View SolutionA torque of `20 N-m` is applied on a wheel initially at rest. Calculate the angular momentum of the wheel after `3` sec.
View SolutionShow that angular momentum of a satellite of mass `M_(s)` revolving around earth of mass `M_(e)` in an orbit of radius `r` is `sqrt(GM_(s)^(2)M_(e)r)`.
View SolutionCalculate angular momentum to Neptune about the sun. Given, mass of neptune `= 10^(12) m` and period of revolution around the sun` = 5 xx 10^(9)s`.
View SolutionAt any instant,`overset rarr(F) = (4.0 hatj)N` acts on a `0.25kg` object that has position vector `overset rarr(r ) = (2.0hati - 2.0 hatk)m` and velocity `overset rarr(upsilon) = (-5.0 hati + 5.0 hatk) m//s`. About the origin, what are angular momentum and torque acting on the object ?
View SolutionA small particle of mass `m` is projected at an angle `theta` with x-axis with initial velocity `upsilon_(0)` in x-y plane as shown in Fig. Calculate the momentum of the particle
at `t lt (upsilon_(0) sin theta)/(g)`.

View SolutionA car of mass `2500 kg` is moving in a circular track of diameter `100m` with a speed of `72 km//h`. What is the angular momentum of the car ?
View SolutionThe radius of a wheel of car is `0.4m`. The car is accelerated from rest by an angular acceleration of `1.5 rad//s^(2)` for `20 s`. How much distance will the wheel cover in this time and what will be its linear velaocity ?
View SolutionA flywheel rotating at a speed of `600` rpm about its axis is brough to rest by applying a constant torque for `10` seconds. Find the angular deceleration and angular velocity `5` second after the application of the torque.
View SolutionObtain the equation `omega = omega_(0) alpha t` from first principles.
View SolutionA flywheel of mass 1 metric ton and radius `1 m` is rotating at the rate of `420` rpm. Find the constant retarding torque required to stop the wheel in `14` rotations, assuming mass to be concentrated at the rim of the wheel.
View SolutionA dics rotates about the central axis starting from rest and accelerates with constant angular accelertion. At one time, it is rotating at `10 rps` , `60` revoluting later, its angular speed is `15rps`. Calculate (i) angular acceleration (ii) time required to complate `60` revols (iii) the time required to reach `10 rev//sec` angular speed and (iv) number of revoluting from rest until the time the disc reaches `10rps` angular speed.
View SolutionA disc of radius `0.5 m` is rotating about an axis passing through its centre and perpendicular to its plane. A tangential force of `2000 N` is applied to bring the disc to rest `2 s`. Calculate its abgular momentum.
View SolutionA moton car is travelling at `30 m//s` on a circular road of radius `500m`. It is increasing in speed at the rate of `2 ms^(-2)`. What is its acceleration ?
View SolutionAn energy of `484 J` is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Calculate moment of inertia of flywheel.
View SolutionA soild sphere is rolling on a frictionless plane surface about the axis of symmetry. Find the rotational energy of the sphere. Also, find the ratio of rotational `K.E.` to total energy.
View SolutionThe moment of inertia of a body about a given axis is `1.2 kg m^(2)`. Initially, the body is at rest. In order to produce a rotational `KE` of `1500 j`, for how much duration, an acceleration of `25 rad s^(-2)` must be applied about that axis ?
View SolutionA thin hollow cylinder open at both ends and weight `5 kg` (i) slides with a speed of `5m//s` without rotating and (ii) rolls with the same speed without slipping. Compare the `KE` of the cylinder in the two cases.
View SolutionA spherical ball of radius `r` and mass `m` is rolling without slipping on a horizontal table. Calculate the percentage of `KE`, which is translational.
View SolutionA disc of radius `0.5 m` is rotating about an axis passing through its centre and perpendicular to its plane. A tangential force of `2000 N` is applied to bring the dics to rest `2 s`. Calculate its abgular momentum.
View SolutionA flywheel of mass `25 kg` has a radius of `0.2 m`. It is making 240 rpm. What is the torque necessary to bring it to rest in `20 s` ? If the torque is due to a force applies tangentially on the rim of the wheel, what is the magnitude of the force ? Assume that mass of flywheel is concentrated at its rim.
View SolutionShow that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
View SolutionShow that moment of a couples does not depend on the point about which you take the moments.
View SolutionA metal bar `70 cm` long and `4.00 kg` in mass is supported on two knife edges placed `10 cm` from each end. A `6.00 kg` weight is suspended at `30 cm` from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
View SolutionA car moves on a road with a speed of `54 km h^(-1)`. The radius of its wheels is `0.35 m`. What is the average negative torque transmitted by its brakes to the wheels if the car is brought to rest in `15 s`? Moment of inertia of the wheels about the axis of rotation is `3 kg m^(2)`.
View SolutionA grindstone has moment of inertia of `6 kg m^(2)`. A constant torque is applied and the grindstone is found to have a speed of `150` rpm, 10 second after satrting from rest. Calculate the torque.
View SolutionA body whose moment of intertia is `3 kg m^(2)` is at rest. It is rotated for `20 s` with a moment of force `6 N-m`. Find angular displacement of the body. What is work done ?
View SolutionA wheel, initially at rest, rotates for `2 s` under angular acceleration of `3 rad s^(-2)`. Find (i) angular velocity acquired in `2 s`.
(ii) angular displacement in `2 s`.
(ii) torque acting on the wheel if its moment of inertia is `12 kg m^(2)`.
View SolutionA cylinder of mass `5 kg` and radius `30 cm` and free to rotate about its axis receives an angular impulse of `3 kg m^(2) s^(-1)` initially, followed by a similar impulse after every `4` second. What is the angular speed of the cylinder `30 s` after the initial impulse ? The cylinder is at rest initially.
View SolutionTo speed up a flywheel from 60rpm to 120 rpm, energy equal to `9000 J` is requires. Calculate the moment of inertia of flywheel. Also calculate change in angular momentum of flywheel.
View SolutionWhat will be the duration of the day, if the earth suddenly shrinks to `1//64 th` of its original volume, mass remaining unchenged ?
View SolutionThe maximum and minimum distances of a comet from the sun `1.4 xx 10^(12) m` and `7 xx 10^(10) m`. If its velocity nearest of the sun is `6 xx 10^(4) ms^(-1)`. What is its velocity at the farthest position ? Assume that path of commet in both the instantaneous position is circular.
View SolutionA horizontal disc ratating about a vertical axis passing through its centre makes `180` rpm. A small piece of wax of mass `10 g` falls vertically on the disc and stricks to it at a distance reduced to `150 rpm`, calculate moment of inertia of the disc.
View SolutionA ball tied to a string takes `4 s` to complete one revoluting along a horizontal circule. If by pulling the cord, the radius of the circle is reduced to half, how much time will the ball take to complete one revolution ?
View SolutionA preson is standing on the centre of a rotating table with his arms outstretched. The table is rotating freely with an angular his hands towards his chest. The moment of inertia reduces to `(3)/(5)` time the original moment of inertia. Calculate angular speed of the man when he withdraws his hands.
View SolutionIf the earth suddenly contracts to one third of its present size, calculate by how much would the day be shortened ?
View SolutionA disc of moment of inertia `I_(1)` is rotating freely with angular speed `omega_(1)` when another non-rotating disc of moment of inertia `I_(2)` is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
View SolutionCalculate the moment of inertia of a uniform rod of mass `M` and length `l` about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.

View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass `M` and radius `R` about an axis which is tangent ot the ring and (`a`) in the plane of the ring (`b`). perpendicular to the plane of the ring.
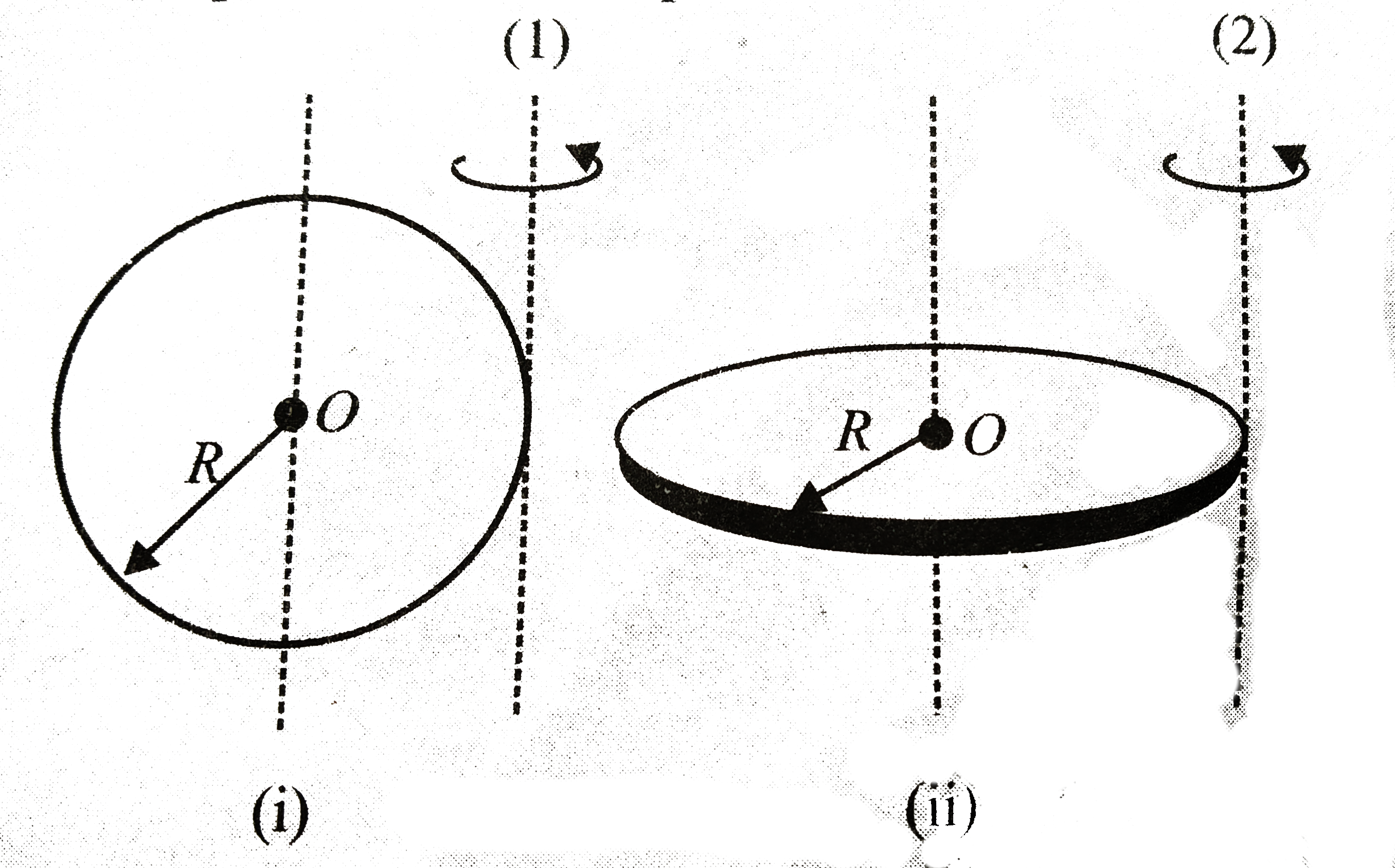
View SolutionFour spheres, each of diameter `2a and mass M` are placed with their centres on the four corners of a square of side `b`. Calculate one side of the square taken as the axis.
View SolutionFind the moment of inertia of a rectangular bar magent about an axis passing through its centre and parallel to its thickness. Mass of magent is `100 g`, its length is `12 cm`, breadth is `3 cm` and thickness is `2 cm`.
View SolutionCalculate the moment of inertia of a cylinder of length `1.5 m`, radius `0.05m` and density `8 xx 10^(3) kg//m^(3)` about the axis of the cylinder.
View SolutionThree balls of masses `1 kg, 2 kg and 3 kg` are arranged at the corners of an equilateral triangle of side `1 m`. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionA circular ring of radius `10 cm` is made of a wire of mass `0.02 g//cm`. Calculate its radius of gyration and moment of inertia about an axis passing perpendicular to its plane through the centre of the ring.
View SolutionA soild cylinder rolls down an inclined plane. Its mass is `2 kg and radius 0.1 m`. It the height of the inclined plane is `4m`, what is its rotational `K.E.` when it reaches foot of the plane ? Assume that the surfaces are smooth. Take `M.I.` of soild cylinder about its axis = `mr^(2)//2`.
View SolutionA `70kg` man stands in contact against the inner wall of a hollow cylindrical drum of radius `3m` rotating about its verticle axis. The coefficient of friction between the wall and his clothing is `0.15` . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA `3m` along ladder weighing `20 kg` leans on a frictionless wall. Its feet rest on the floor `1 m` from the wall. Find the rection forces of the wall and the floor.
View SolutionThe angular speed of a moton wheel is increased from `1200` rpm to 3120 rpm in `16` seconds. (i) What is the angular acceleration, assuming the acceleration to be uniform ? (ii) How many revolutions does the engine make during this time ?
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass `20 kg` and radius `20 cm`. A steady pull of `25 N` is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
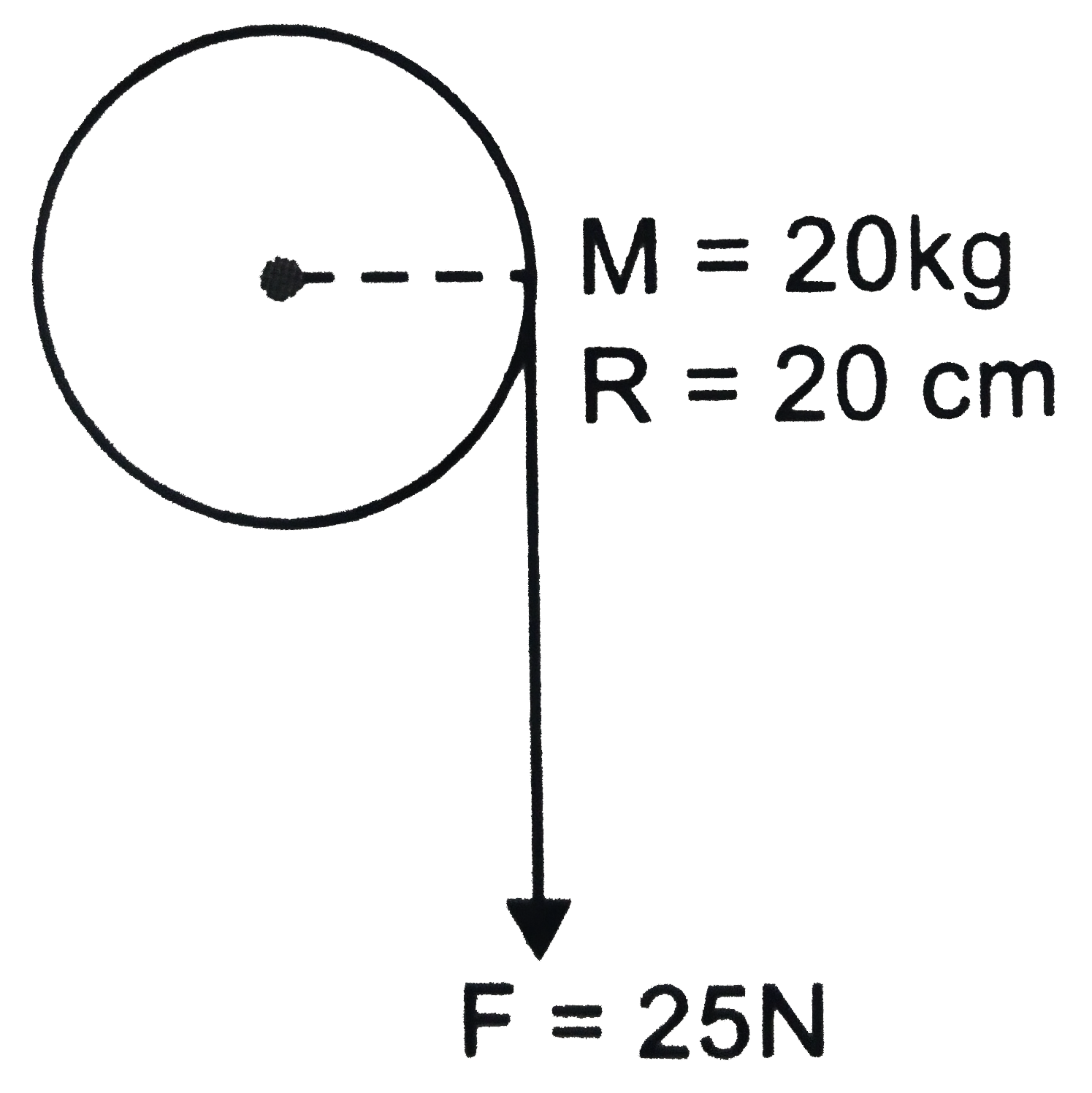
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when `2 m` of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionThree bodies, a ring, a soild cylinder and a soild sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity ?
View SolutionA body of mass `5 kg` is attached to a weightless string wound round a cylinder of mass `8 kg` and radius `0.3 m`. The body is allowed to fall. Calculate (i) tension in the string, (ii) acceleration with which the body falls and (iii) angular acceleration of the cylinder.
View SolutionThe moment of inertia of a body about a given axis is `1.2 kg m^(2)`. Initially, the body is at rest. In order to produce a rotational `KE` of `1500 J`, for how much duration, an acceleration of `25 rad s^(-2)` must be applied about that axis ?
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- ADDITIONAL EXERCISES
- ADVANCED PROBLEMS FOR COMPETITIONS
- Assertion- Reason Type questions
- CONCEPTUAL PROBLEMS
- CONCEPTUAL PROBLEMS I.
- CONCEPTUAL PROBLEMS II.
- CURIOSITY QUESTIONS
- FILL IN THE BLANKS
- Focus Multiple Choice Questions I.
- Integer Type Questions
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- Multiple Choice Questions Comprehension 2
- Multiple Choice Questions II.
- Multiple Choice Questions III. Comprehension 1
- MULTIPLE CHOICE QUESTIONS-I
- MULTIPLE CHOICE QUESTIONS-II
- NCERT
- PROBLEMS FOR PRACTICE
- PROBLEMS FOR PRACTICE TYPE A
- PROBLEMS FOR PRACTICE TYPE B
- PROBLEMS FOR PRACTICE TYPE C
- PROBLEMS FOR PRACTICE TYPE D
- PROBLEMS FOR PRACTICE TYPE E
- QUESTIONS
- Sample problem
- SHORT ANSWER QUESTIONS
- SHORT ANSWER QUESTIONS I.
- SHORT ANSWER QUESTIONS II.
- SOLVED EXAMPLES
- SOLVED EXAMPLES TYPE A
- SOLVED EXAMPLES TYPE B
- SOLVED EXAMPLES TYPE C
- SOLVED EXAMPLES TYPE D
- SOLVED EXAMPLES TYPE E
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS
- VERY SHORT ANSWER QUESTIONS I.
- VERY SHORT ANSWER QUESTIONS II.