Complete Solutions to Exercise of chapter KINEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| RESONANCE | Exercise |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
A particle moves along a path `ABCD` as shown in the figure. Then the magnitude of net displacement of the particle from position `A` to `D` is:

View SolutionA particle starts from rest with uniform acceleration `a`. Its velocity after 'n' second is 'v'. The displacement of the body in the last two second is
View SolutionA particle whose speed in 50 m/s moves along the line from A(2, 1) to B(9, 25). Find its velocity vector in the form of `a hat(i) + b hat(j)`.
View SolutionA clock a minute-hand `10 cm` long. Find the average velocity between `6.00 AM` to `6.30 AM` for the tip of minute-hand.
View SolutionA particle is moving in a circle of radius `r` with speed `v` as shown in the figure. The magnitude of change in velocity in moving from `P` to `Q` is
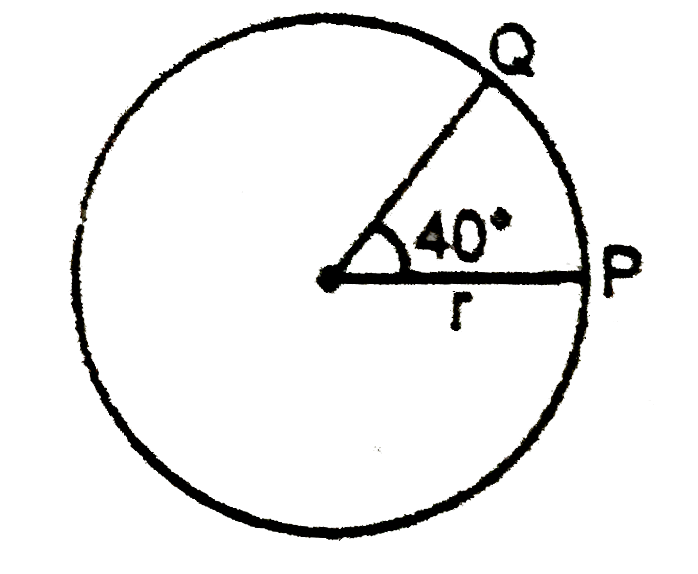
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in `nth` second to that covered in `n` second is.
View SolutionTwo bikes `A and B` start from a point. A moves with uniform speed `40 m//s and B` starts from rest with uniform acceleration `2 m//s^2`. If `B` starts at `t = 10` and `A` starts from the same point at `t = 10 s`, then the time during the journey in which `A` was ahead of `B` is :
View SolutionA stone is dropped from the top of tower. When it has fallen by `5 m` from the top, another stone is dropped from a point `25m` below the top. If both stones reach the ground at the moment, then height of the tower from grounds is : (take `g=10 m//s^(2)`)
View SolutionFor a particle moving in a straight line, the displacement of the particle at time `t` is given by
`S=t^(3)-6t^(2) +3t+7`
What is the velocity of the particle when its acceleration is zero?
View SolutionThe displacement time graphs of two bodies `A` and `B` are shown in figure. The ratio of velocity of `A` to velocity of `B, v_(A)//v_(B)` is:

View SolutionThe force acting on a particle moving along a straight line varies with time as shown in diagram.
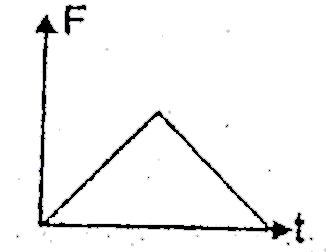
Which of the following graphs is best representative of its speed and time graphs. Initial velocity the particle is zero.
View SolutionA particle initially at rest is subjected to two forces, one is constant, the other is retarding force proportional to the particle velocity. In the subsequent motion of the particle, the acceleration
View SolutionVelocity `(v)` versus displacement (s) graph of a particle moving in a straight line is shown in figure. Corresponding acceleration (a) versus velocity (v) graph will be
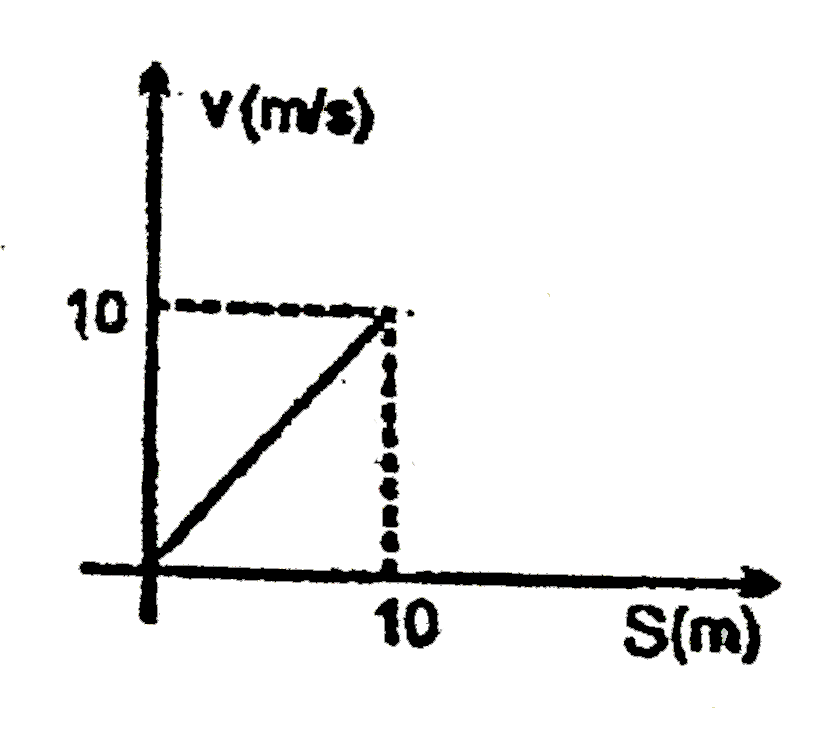
View SolutionDisplacement-time curve of a particle moving along a straight line is shown. Tangents at `A` and `B` makes angle `45^(@)` and `135^(@)` with positive `x`-axis respectively. The average acceleration of the particle during `t=1,t=2` seconds is
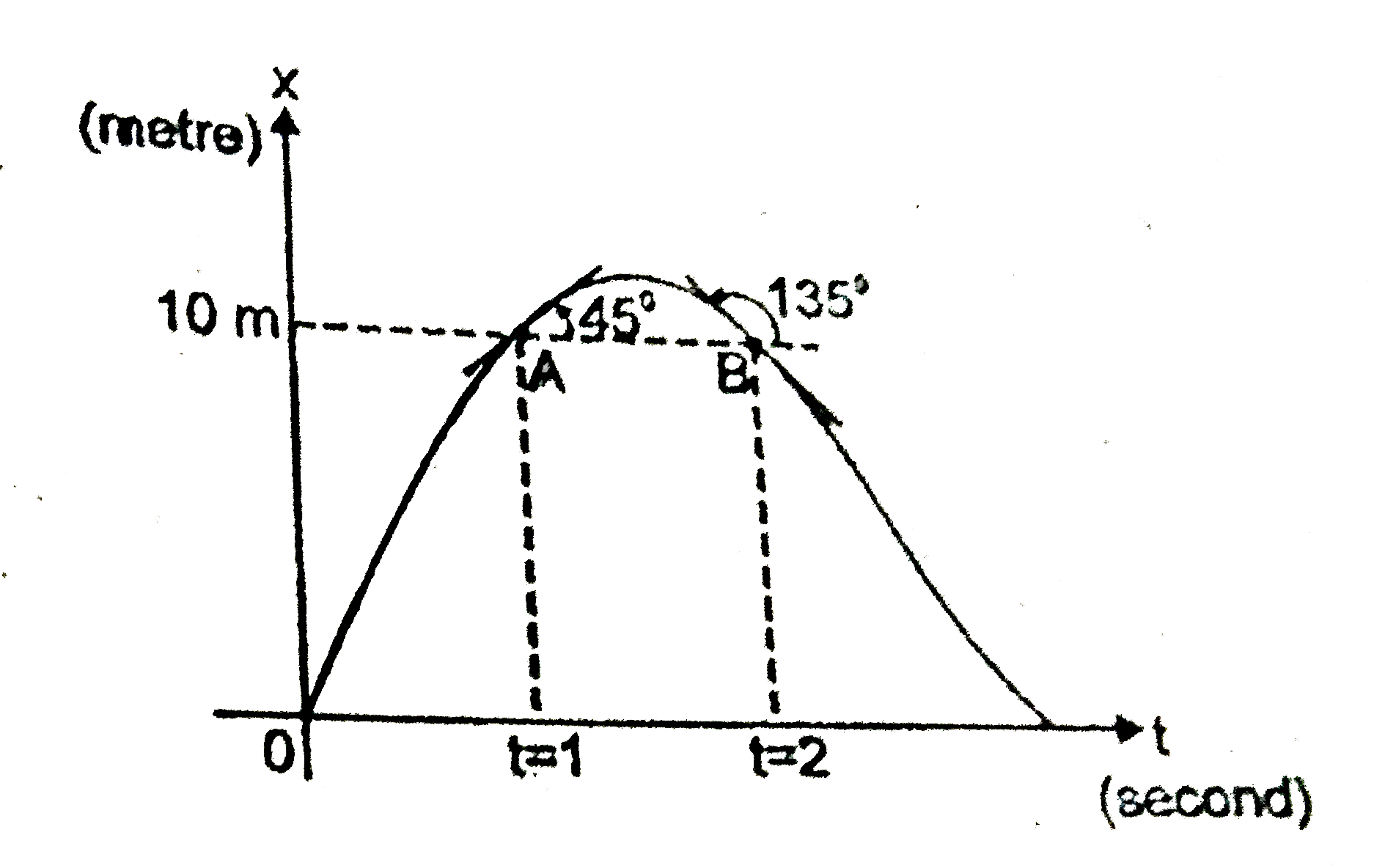
View SolutionTwo identical balls are shot upward one after another at an interval of 2s along the same vertical line with same initial velocity of `40 ms^-1`. The height at which the balls collide is
View SolutionA stone thrown upwards with a speed u from the the top of the tower reaches the ground with a speed 3u. The height of the tower is
View SolutionThree particles are projected upwards with initial speeds `10 m//s,20 m//s,30 m//s`. The displacements covered by them in their last second of motion are `x_(1),x_(2),x_(3)` then:
View SolutionA ball is thrown vertically upwards from the top of tower of height `h` with velocity `v` . The ball strikes the ground after time.
View SolutionParticle is projected along a rough horizontal table, its path must be : (assuming only gravity and contanct force due to the table acting).
View SolutionA particle is resting over a smooth horizontal floor. At `t = 0,` a horizontal force starts acting on it. Magnitude of the force increases with time according to law `F = alpha t,` Where alpha is a positive constant. From figure, which of the following statements are correct ?
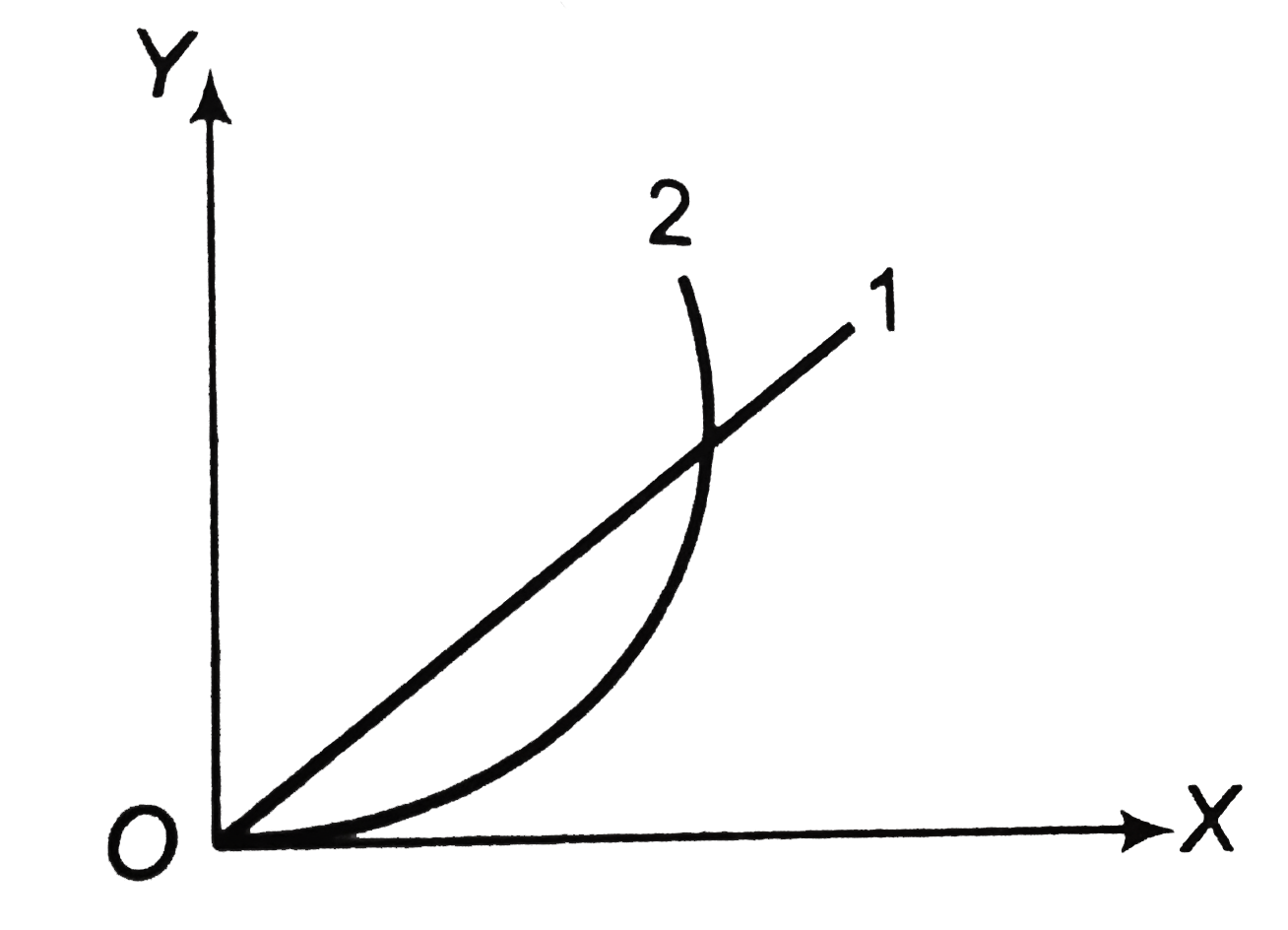
View SolutionA particle is moving with initial velocity `bar(u)=hati-hatj+hatk`. What should be its acceleration so that it can remain moving in the same straight line?
View SolutionA particle moving along a straight line with a constant acceleration of `-4 m//s^(2)` passes through a point `A` on the line with a velocity of `+8 m//s` at some moment. Find the distance travelled by the particle in `5` seconds after that moment.
View SolutionA moving train is stopped by applying brakes. It stops after travelling `80 m`. If the speed of the train is doubled and retardation remain the same, it will cover a distance-
View SolutionA particle starts from rest and moves along a straight time with constant acceleration. The variation of velocity v with displacement s is
View SolutionA body starts from rest, what is the ratio of the distance travelled by the body during the 4th and 3rd s?
View SolutionThe initial velocity of a body moving along a straight lines is `7m//s`. It has a uniform acceleration of `4 m//s^(2)` the distance covered by the body in the `5^(th)` second of its motion is-
View SolutionAcceleration of a particle under projectile motion at the highest point of its trajectory is :
View SolutionA particle `A` is projected with speed `V_(A)` from a point making an angle `60^(@)` with the horizontal. At the same instant, a second particle `B` is thrown vertically upwards from a point directly below the maximum height point of parabolic path of A, with velocity `V_(B)` . If the two particles collide then the ratio of `V_(A)//V_(B)` should be:
View SolutionA particle is projected from a horizontal floor with speed `10 m//s` at an angle `30^(@)` with the floor and striking the floor after sometime. State which is correct.
View SolutionA particle is projected up the inclined such that its component of velocity along the incline is `10 m//s`. Time of flight is `2` sec and maximum height above the incline is `5m`. Then velocity of projection will be
View SolutionA particle P is projected from a point on the surface of a smooth inclined pane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same postion. P and Q colide on the inclined plane after `t=4` seconds. Find the speed projection in m/s.
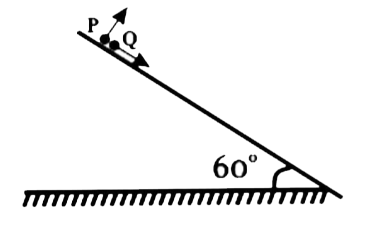
View SolutionVelocity of a stone projected, 2 second bofore it reaches the maximum height makes angle `53^@` with the horizontal then the velocity at highest point will be
View SolutionA stone projected at angle `theta` with horizontal from the roof of a tall building falls on the ground after three seconds. Two second after the projection it was again at the level of projection. Then the height of the building
View SolutionA stone projected at angle `53^(@)` attains maximum height 25m during its motion in air. Then its distance from the point of projection where it will fall is
View SolutionA particle is projected with speed `10 m//s` at angle `60^(@)` with the horizontal. Then the time after which its speed becomes half of initial.
View SolutionA stone is projected with speed `20 m//s` at angle `37^(@)` with the horizontal and it hits the ground with speed `12m//s` due to air resistance. Assume the effect of air resistance to reduce only horizontal component of velocity. Then the time of flight will be-
View SolutionSpeed at the maximum height of a projectile is half of its initial speed `u`. Its range on the horizontal plane is `:`
View SolutionDistance between a frog and an insect on a horizontal plane is 10m. Frog can jump with a maximum speed of `sqrt(10) m//s`. Minimum number of jumps required by the frog to catch the insect is : `g=10 m//s^2`.
View SolutionA stone is projected from point `A` with speed `u` making an angle `60^(@)` with horizontal as shown. The fixed inclined surface makes an angle `30^(@)` with horizontal. The stone lands at `B` after time `t`. Then the distance `AB` is equal to .

View SolutionA projectile can have the same range 'R' for two angles of projection . If `'T_(1)'` and `'T_(2)'` to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .
View SolutionTwo stones are projected from level ground. Trajectory of two stones are shown in figure. Both stones have same maximum heights above level ground as shown. Let `T_(1)` and `T_(2)` be their time of flights and `u_(1)` and `u_(2)` be their speeds of projection respectively (neglect air resistance). then
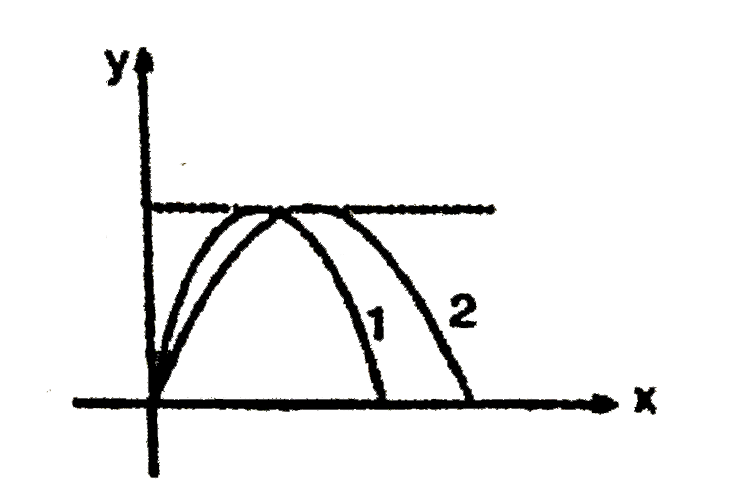
View SolutionOne stone is projected horizontally from a `20 m` high cliff with an initial speed of `10 ms^(-1)`. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View SolutionA small rolls of the top of a stairway horizontally with a velocity of `4.5 ms^(-1)`. Each step is 0.2 m high and 0.3 m wide. If g is `10ms^(-2)`, then the ball will strike the nth step where `n` is equal to (assume ball strike at the edge of the step).
View SolutionA projectile is thrown with velocity v making an angle `theta` with the horizontal. It just crosses the top of two poles,each of height h, after 1 seconds 3 second respectively. The time of flight of the projectile is
View SolutionAn arrow is shot in air, its time of flight is 5 sec and horizontal range is 200 m. the inclination of the arrow with the horizontal is
View SolutionTwo projectiles are projected angle `((pi)/(4) + theta)` and `((pi)/(4) - theta)` with the horizontal , where `theta lt (pi)/(4)`, with same speed. The ratio of horizontal ranges described by them is
View SolutionThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [`g=10 m//s^(2)`]
View SolutionAn eaeroplane is to go along straight line from A to B, and back again. The relative speed with respect to wind is V. The wind blows perpendicular to line AB with speed v. The distance between A and B is `l`. The total time for the round trip is:
View SolutionA man crosses the river perpendicular to river in time t seconds and travels an equal distance down the stream in T seconds. The ratio of man's speed in still water to the river water will be:
View SolutionPassenger of a train just drops a stone from it. The train was moving with constant velocity. What is path of the stone as observed by (a) the passenger itself, (b) a man standing on ground?
View Solution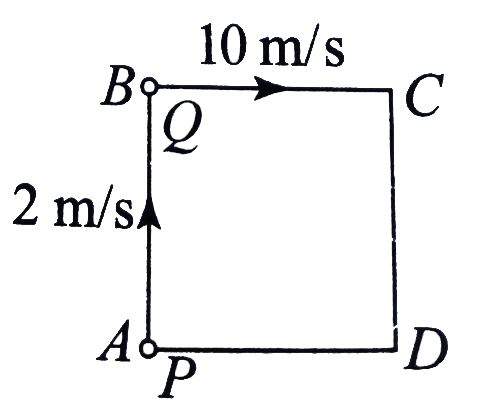
Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed `2(m)/(s)` and `10(m)/(s)` respectively. Find the time when they will meet for the first time
View SolutionP is a point moving with constant speed `10 m//s` such that is velocity vector always maintains an angle `60^(@)` with line OP as shown in figure (O is a fixed point in space). The initial distance between O and P is 100 m.

View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of `9 m//s^(2)`downwards. The time after which the coin will strike with the lift is : `(g=10 m//s^(2))`
View SolutionA man is holding an umbrella at angle `30^(@)` with vertical with lower end towards himself, which is appropriate angle to protect him from rain for his horizontal velocity `10 m//s` . Then which of the following will be true-

View SolutionA man is sitting inside a moving train and observes the stationary objects outside of the train. Then choose the single correct choice from the following statements`-`
View SolutionWhich of the following is true ?
View SolutionTwo particles are moving along a straight line as shown. The velocity of approach between A and B is
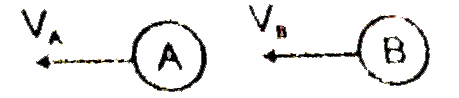
View SolutionA man who can swin at the rate of 2 `(km)/hr)`(in still river) crosses a river to a point exactly opposite on the other bank by swimming in a direction of `120^@` to the flow of the water in the river. The velocity of the water current in `(km)/(hr)` is
View SolutionA river is flowing from west to east at a speed of ` 5 metres per minute` . A man on the south bank of the river , capable of swimming at `10 metres per minute`, in still water , wants to swim across the river in the shortest time . He should swim in a direction
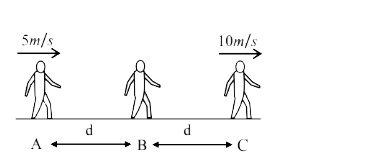
View SolutionThree persons A, B and C are moving along a straight line with constant speed in same direction as shown in figure. Speed of A is 5 m/s and speed of C is 10 m/s. Initially separation between A and B is ‘d’ and between B and C is also d. When ‘B’ catches ‘C’, separation between A and C becomes 3d. Then the speed of B will be:
View SolutionA jet airplane travelling at the speed of `500 km h^(-1)` ejects its products of combustion at the speed of `1500 km h^(-1)` relative to the jet plane. The speed of the products of combustion with respect to an observer on the ground is
View SolutionA man is on ship which is moving in east direction with speed `60km//hr.` Waves of ocean is taking ship towards west with speed `20km//hr`. Man start running on ship with flag in his hand in north direction with speed `30km//hr` and wind is blowing with `50km//hr,37^(@)` towards south of west then find the direction of flutter the flag as seen by man on ground.
View SolutionA battalion of soldiers is ordered to swim across a river `500 m` wide. At what minimum rate should they swim perpendicular to river flow in order to avoid being washed away by the waterfall 300 m downstream. The speed of current being 3m/sec:
View SolutionA stone is just released from the window of a train moving along a horizontal straight track. The stone will hit the ground in
View SolutionThe motion of a projectile as seen from other projectile is
View Solution
Exercise questions and complete solutions for chapter KINEMATICS of RESONANCE ENGLISH of Class 11