Complete Solutions to Exercise of chapter RIGID BODY DYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS |
| RESONANCE | Exercise |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
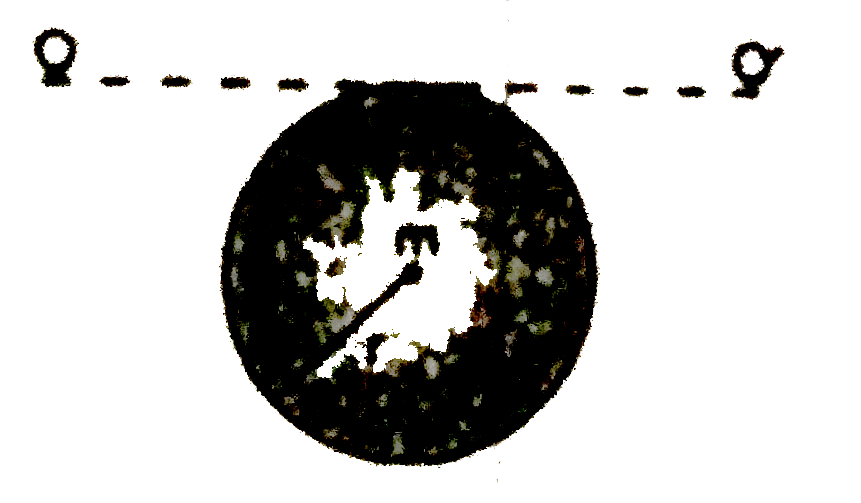
Moment of inetia of a disc about OO' is
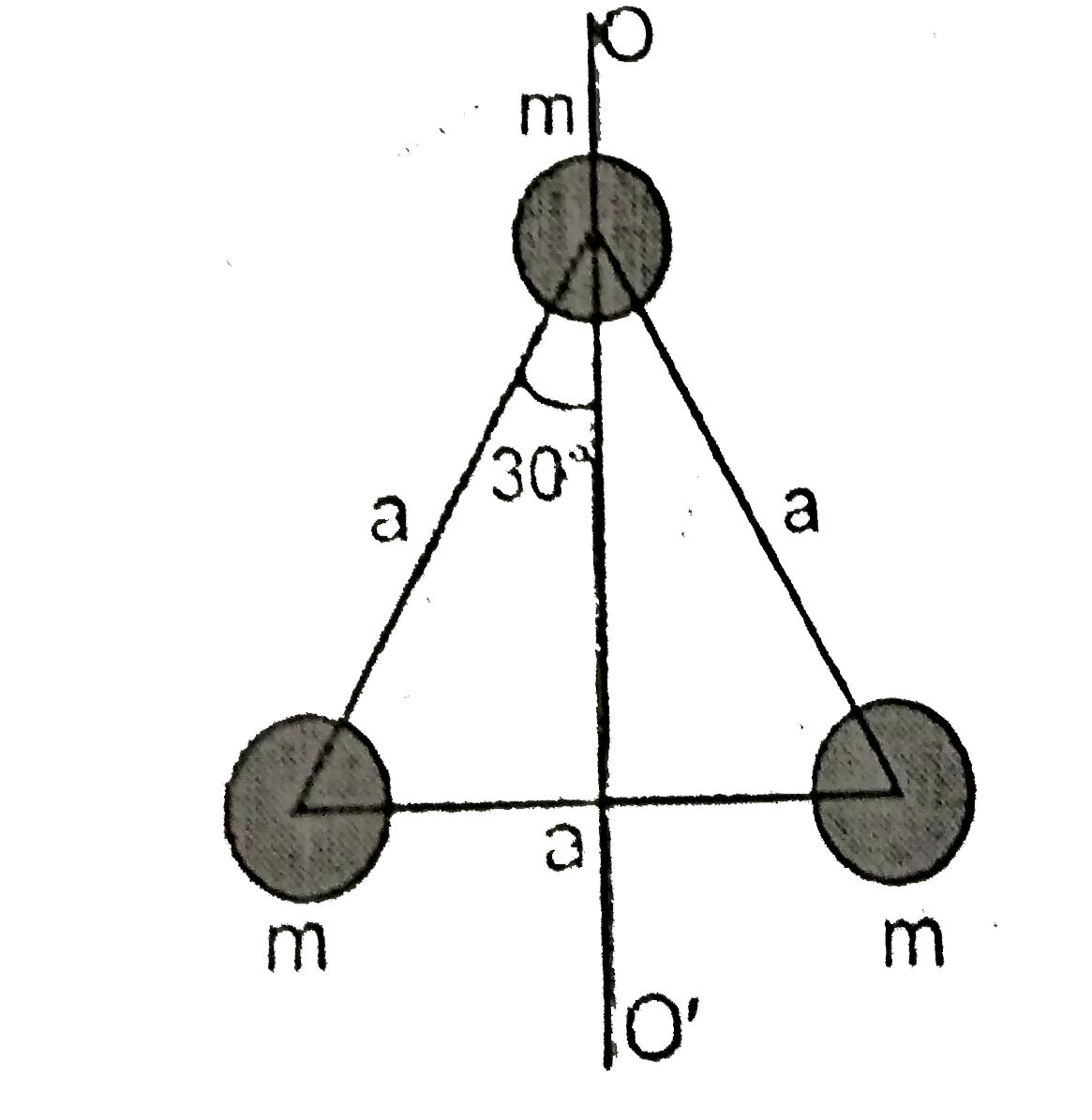
View SolutionThree point masses are arranged as shown in the figure. Moment of inertia of the system about the axis `O O'` is `: (` passing through its plane `)`
View SolutionA thin wire of length `L` and uniform linear mass density `rho` is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis `XX'` is
View SolutionThree identical rods, each of length `L`, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing thorugh a corner and perpendicular to plane of triangle is
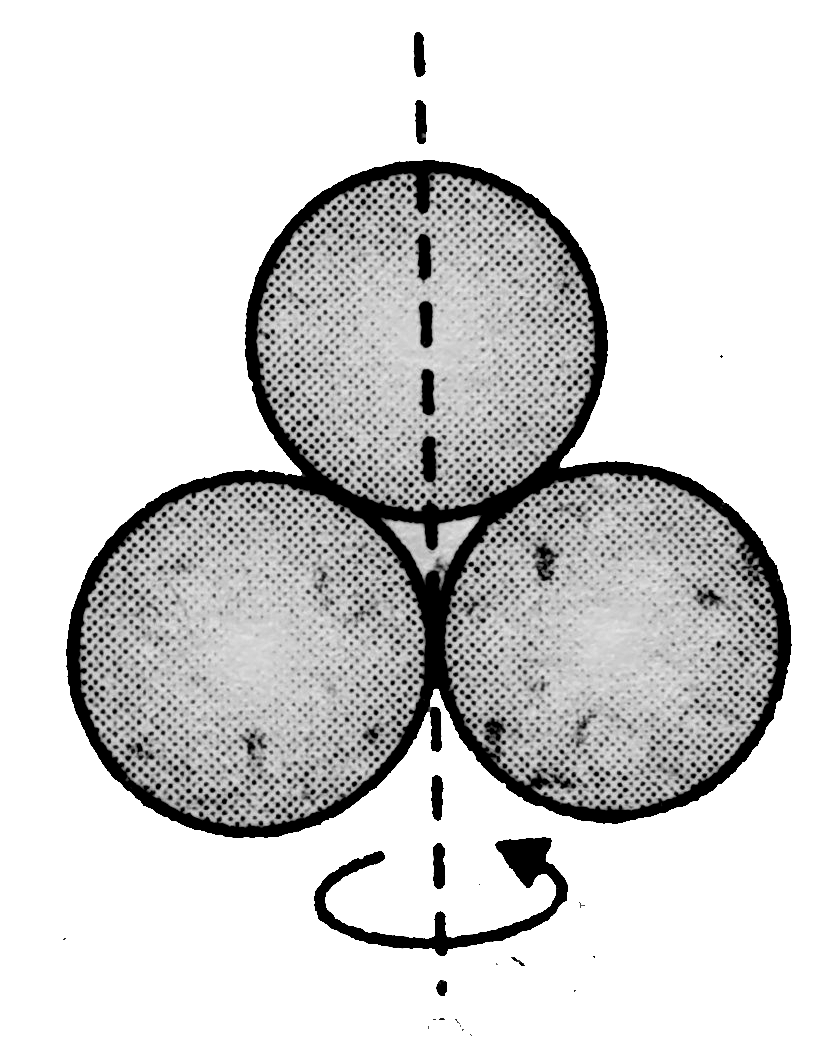
View SolutionThree rings, each of mass `m` and radius `r`, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
View SolutionThe moment of inertia of a door of mass `m`, length `2l` and width `l` about its longer side is
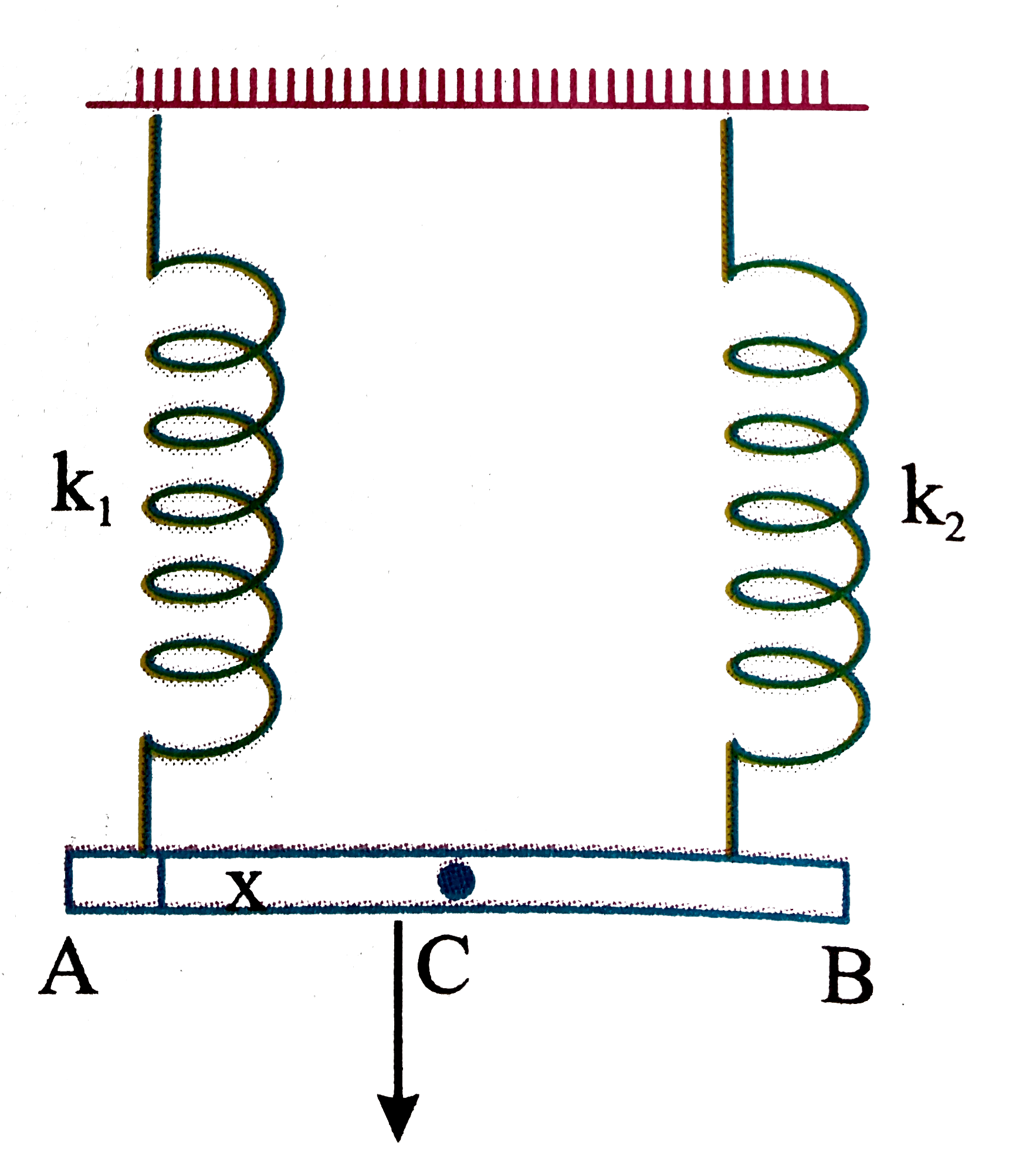
View SolutionTwo light vertical springs with equal natural length and spring constants `k_(1)` and `k_(2)` are separated by a distance `l`. Their upper ends are rigidly connected and the lower ends are connected to `A` and `B` of a light horizontal rod `AB`. A vertically downwards force `F` is applied at point `C` on the rod. `AB` will remain horizontal in equilibrium if the distance `AC` is
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings `T_1/T_2` is:
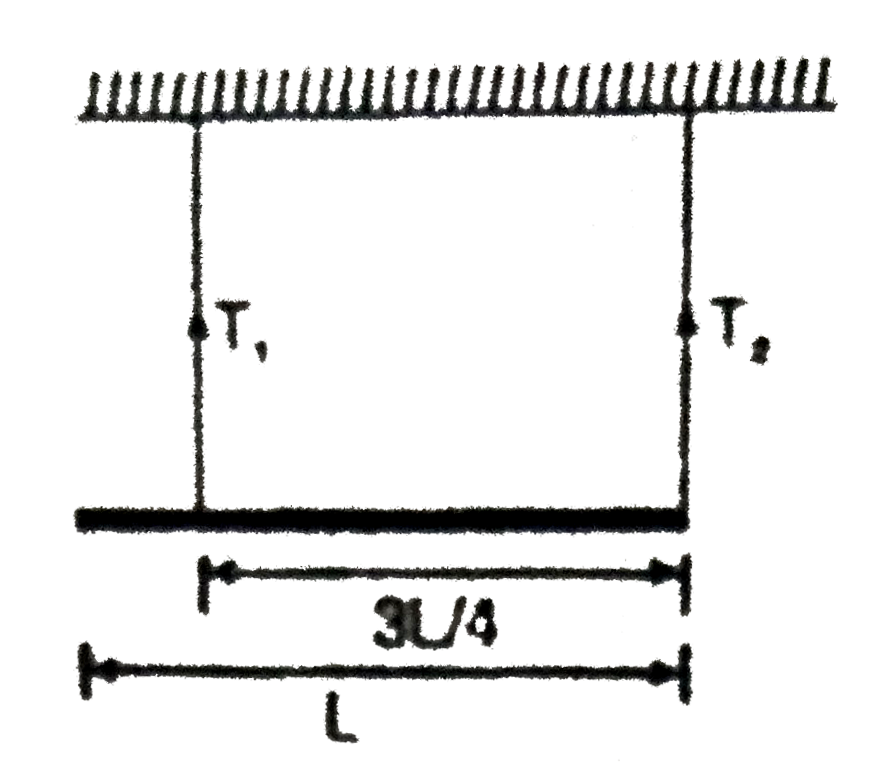
View SolutionTwo persons of equal heights are carrying a long uniform wooden plank of length `l` . They are at distance `(l)/(4)` and `(l)/(6)` from nearest end of the rod. The ratio of normal reaction at their heads is

View SolutionA force `vec(F)=4hati-10 hatj` acts on a body at a point having position vector `-5hati-3hatj` relative to origin of co-ordinates on the axis of rotation. The torque acting on the body is
View SolutionA uniform rod of length L and weight `W_(R)` is suspended as shown in the accompanying figure. A weight W is added to the end of the rod. The rod rests in horizontal position and is hinged at O. the support wire is at an angle `theta` to the rod. What is the tension T in the wire ?

View SolutionTwo points of a rod move with velocities `3v` and `v` perpendicular to the rod and in the same direction rod is separated by a distance `'r'`. The angular velocity of the rod is
View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
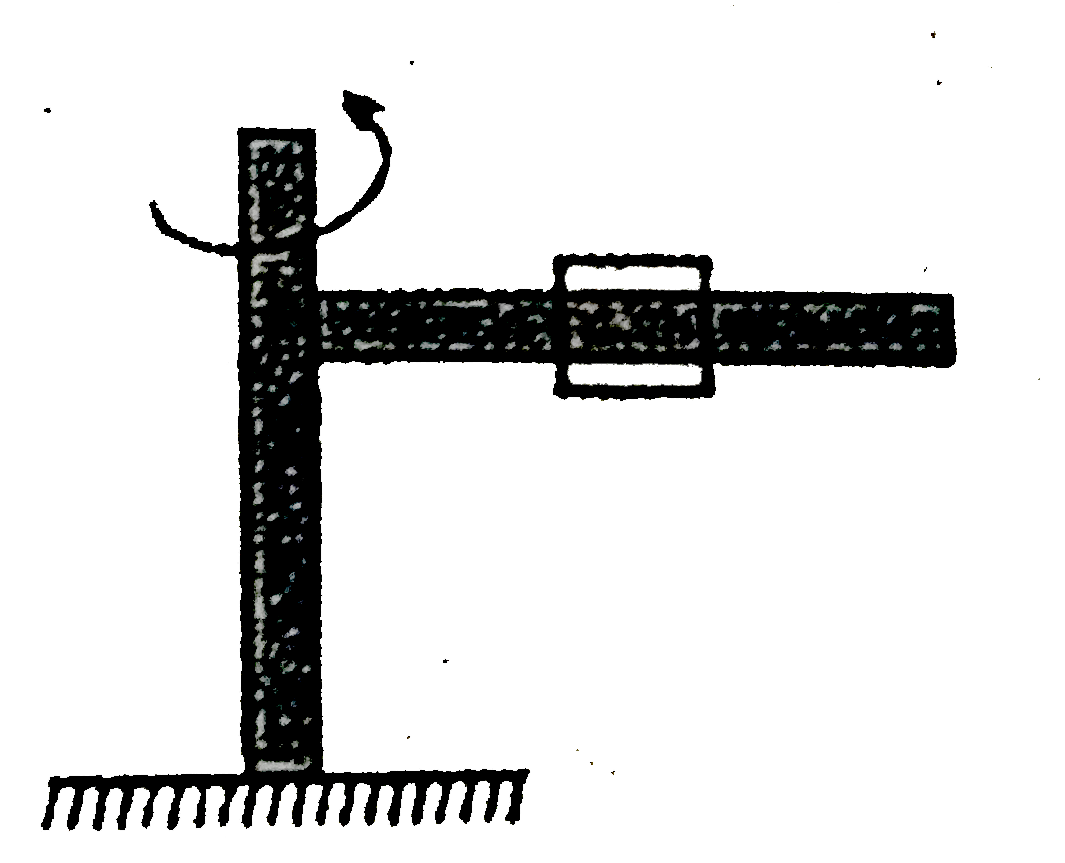
A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
D. the magnitude of friction force on the bead will be variable
View SolutionIn the pully system shown, if radii of the bigger and smaller pulley are 2m and 1m respectively and the acceleration of block A is `5 m//s^(2)` in the downward direction, then the acceleration of block B will be

View SolutionA rod of mass m and length l is kept on a surface that has no friction. If a ball comes & hits the lower end with a velocity v, then the velocity of centre of mass will be

View SolutionIf `vec(tau)xxvec(L)=0` for a rigid body, where `vec(tau)=` resultant torque & `vec(L)` =angular momentum about a point and both are non-zero. Then
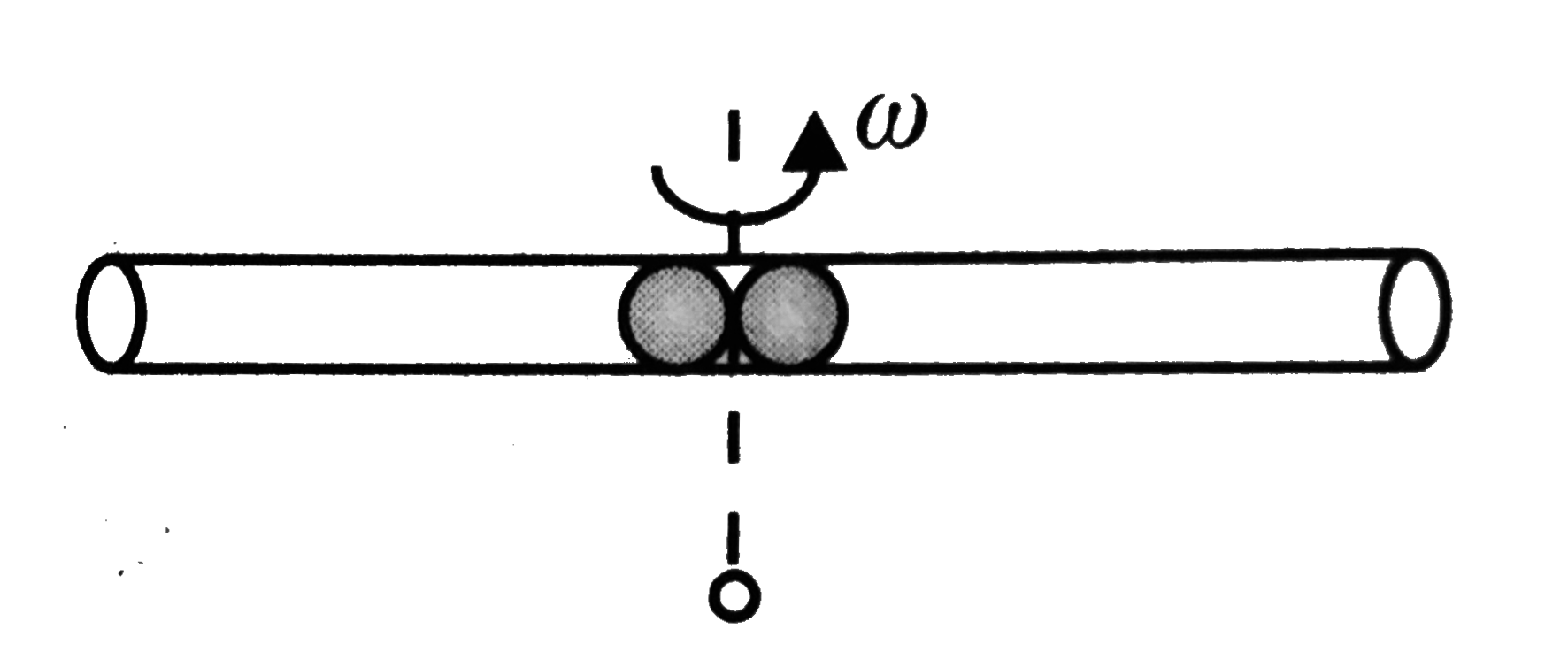
View SolutionA smooth tube of certain mass is rotated in a gravity-free Space and released. The two balls shown in Fig move towards the ends of the tube. For the whole system, which of the following quantities is not conserved.
View SolutionA smooth sphere `A` is moving on a frictionless horizontal plane with angular speed `omega_(A)` and `omega_(B)`, respectively. Then
View SolutionA body of mass m and radius r is rotated with angular velocity `omega` as shown in the figure & kept on a surface that has sufficient friction then the body will move

View SolutionA uniform sphere of radius R is placed on a rough horizontal surface and given a linear velocity `v_(0)` and angular velocity `omega_(0)` as shown. The sphere comes to rest after moving some distance to the right. It follows that

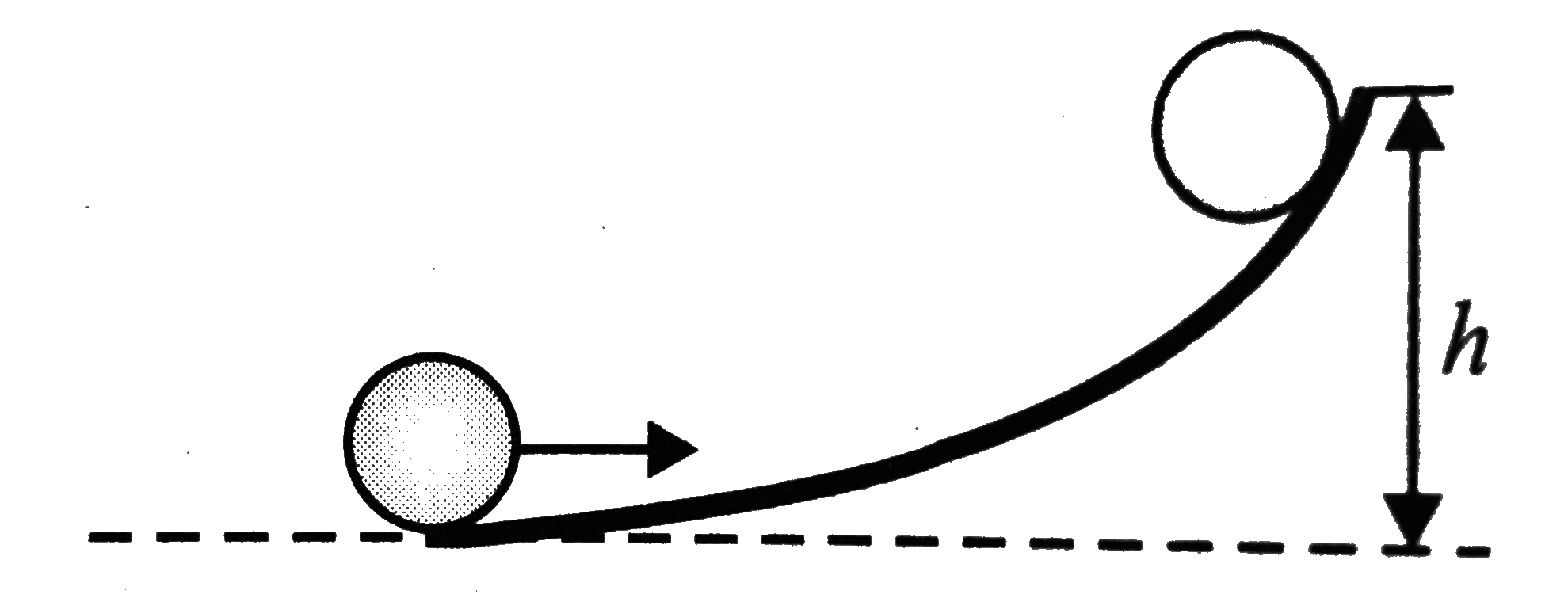
View SolutionIn the figure shown, a ball without sliding on a horizontal, surface. It ascends a curved track up to height `h` returns. The value of h is `h_(1)` for sufficiently rough curved track to avoid sliding and is `h_(2)` for smooth curved track then
View SolutionAs shown in the figure, a disc of mass `m` is rolling without slipping a angular velocity `omega`. When it crosses point `B` disc will be in `:`
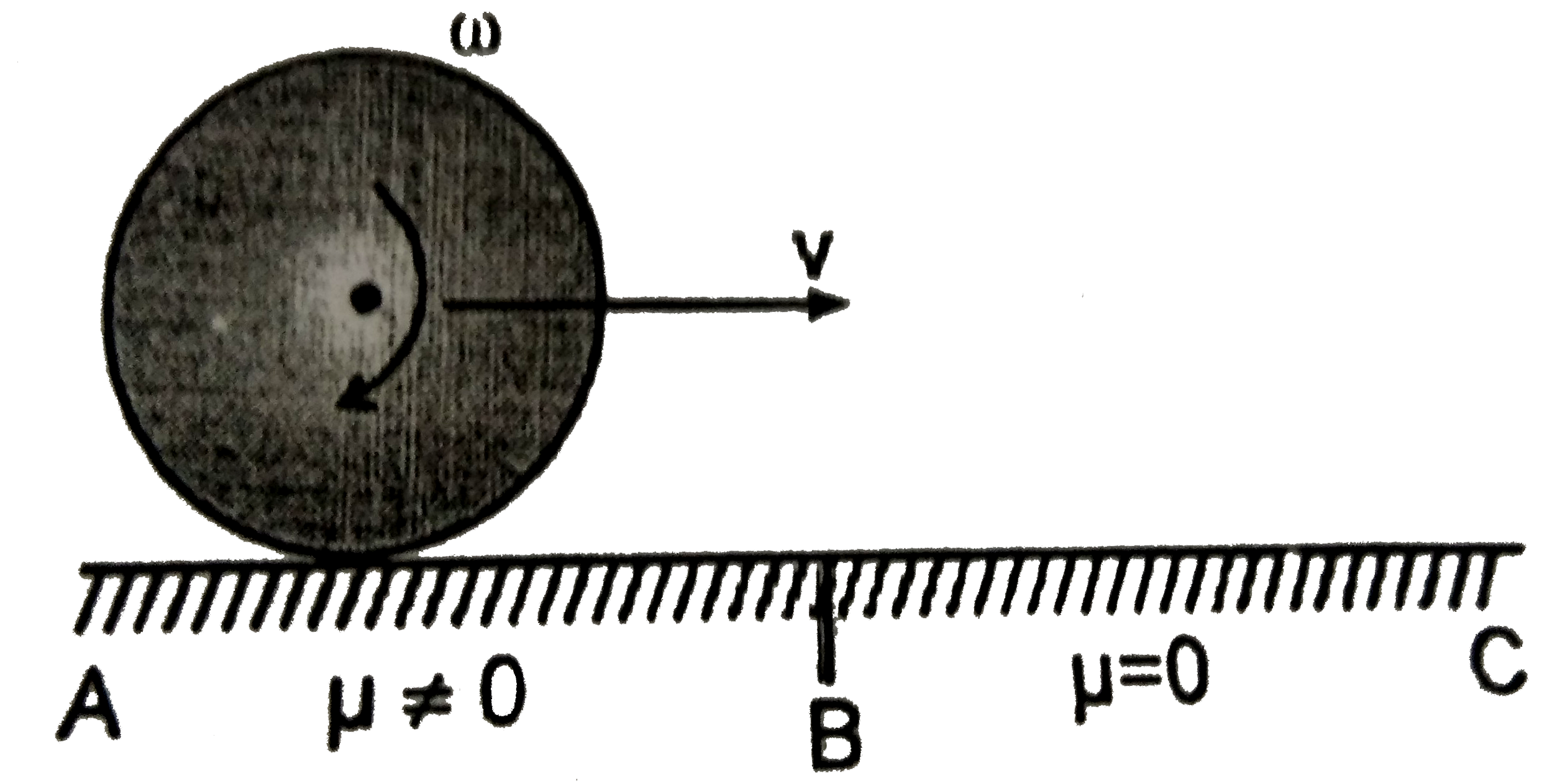
View SolutionWhen a sphere rolls without slipping the ratio of its kinetic energy of translation to its total kinetic energy is.
View SolutionA solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an inclined plane and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
View SolutionIn the previous question the smallest kinetic energy at the bottom of the incline will be achieved by
A. the solid sphere
B. the hollow sphere
C. the disc
D. all will achieve same kinetic energy
View SolutionA box of dimensions l and b is kept on a truck moving with an acceleration a. If box does not slide maximum acceleration for it to remain in equillibrium(with respect to truck) is

View SolutionA rectangular block has a square base measuring `axxa` and its height is `h`. It moves on a horizontal surface in a direction perpendicular to one of the edges. The coefficient of friction is `mu`. It will topple if
View SolutionA weightless rod is acted upon by upward parallel forces of 2N and 4N at ends A and B respectively. The total length of the rod AB=3 m. To keep the rod in equilibrium, a force of 6N should act in the following manner
View SolutionA circular disc `X` of radius `R` is made from an iron of thickness `t`, and another disc `Y` of radius `4R` is made from an iron plate of thickness `t//4`. Then the relation between the moment of mertia `I_(x)` and `I_(Y)` is :
View SolutionA solid spere is rotating freely about its symmetry axis in free space.The radius of the sphere is increased keeping its mass same.Which of the following physical quantites would remain constant for the sphere?
View SolutionA 'T' shaped object with dimension shown in the figure, is lying on a smooth floor. A force F is applied at the point P parallel to AB, such that the objects has only hte translational motion without rotation. Find the location of P with respect to C.
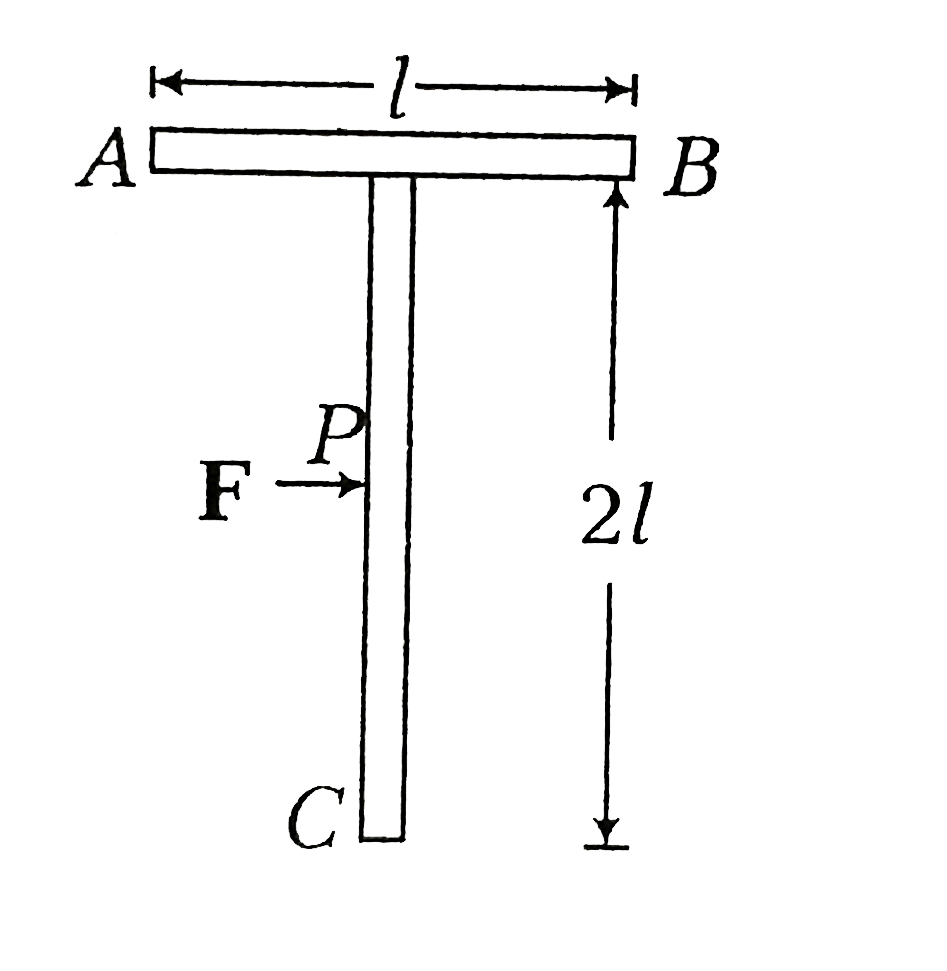
View SolutionAngular momentum of the particle rotating with a central force is constant due to
View SolutionA small paricle of mass m is projected at an angle `theta` with the x-axis with an initial velocity `v_(0)` in the x-y plane as shown in the figure. At a time `tlt(v_(0)sin theta)/(g)`, the angular momentum of the particle is
where `hati, hatj and hatk` are unit vectors along x, y and z-axix respectively.

View Solution`S_(1)`: Net torque on a system due to all internal force about any point is zero.
`S_(2)`: For rigid body undergoing fixed axis rotation, the direction of its angular acceleration and angular velocity
`S_(3)`: if net torque on a rigid body about its centre of mass is zero, the angular speed of the rigid body is always zero.
`S_(4)`: For a rigid body undergoing fixed axis rotation abouts its centre of mass, then net torque on rigid body about any point is same.
View SolutionA rigid body is in pure rotation, that is, undergoing fixed axis rotation. Then which of the following statement(s) are true?
View SolutionA particle falls freely near the surface of the earth. Consider a fixed point `O` (not vertically below the particle) on the ground. Then pick up the correct alternative or alternatives.
View SolutionA particle has a linear momentum p and position vector r. the angular momentum of this particle about the origin will not be zero under the conditions
View SolutionIn the given figure a ball strikes a uniform rod of same mass elastically and rod is hinged at point `A`. Then which of the statements `(s) is//are` correct ?
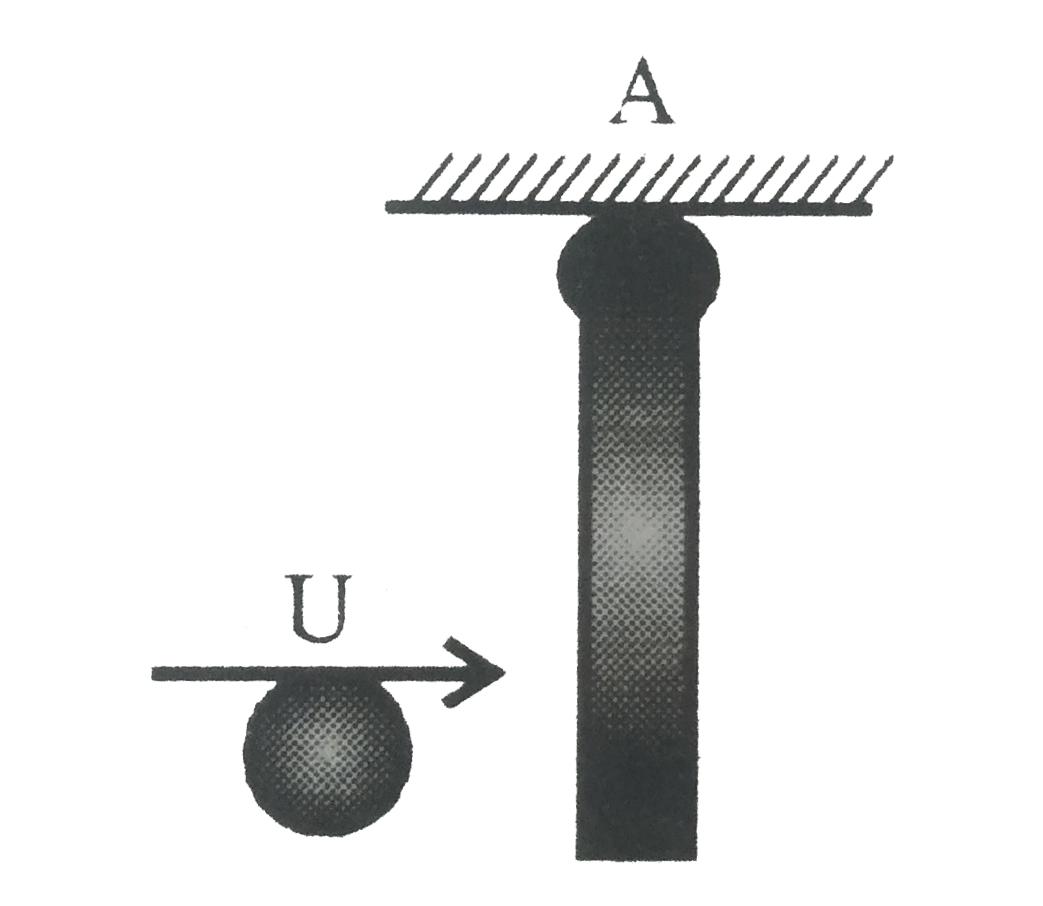 .
.
View SolutionA disc of circumference `s` is at rest at a point `A` on horizontal surface when a constant horizontal force begins, to act on its centre. Between `A` and `B` there is sufficient friction to prevent slipping and the surface is smooth It the right of `B, AB = s`. The disc moves from `A` to `B` in time `T`. To the right of `B`.
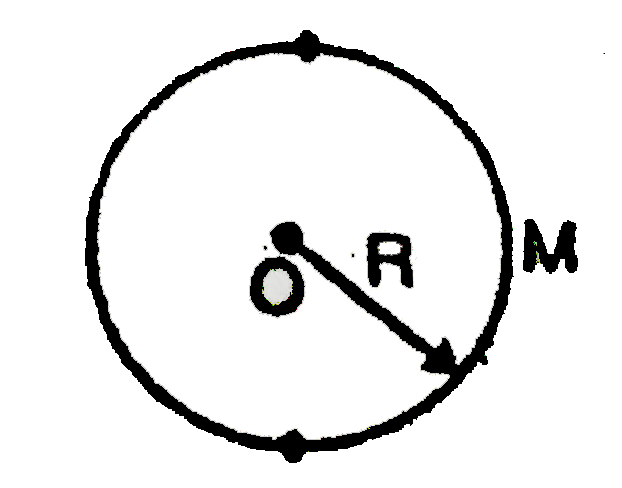
View SolutionA hole of radius R/2 is cut from a thin circular plate of raduis R as shown in the figure. If the mass of the remaining plate is M, then find moment of inertia of the plate about an axis through O perpendicular to plane

A. `13/25 MR^(2)`
B. `13/24 MR^(2)`
C. `11/24 MR^(2)`
D. `11/25 MR^(2)`
View SolutionA uniform disc of mass `m` and radius `R` is rolling up a rough inclined plane which makes an angle of `30^@` with the horizontal. If the coefficients of static and kinetic friction are each equal to `mu` and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View SolutionA uniform cube of side a and mass `m` rests on a rough horizontal table. A horizontal force `F` is applied normal to one of the faces at a point directly above the centre of the face, at a height `(3a)/(4)` above the base. What is the minimum value of `F` for which the cube begins to tip about an edge?
View SolutionIf radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionA disc of mass M and radius R is suspended in a vertical plane by a horizontal axis passing through its centre. After sticking an object of same mass M at its rim the mass is raised to the position of maximum height. Now this unstable system is released. when the object passes the position right below the centre the angular velocity of the system would be
View SolutionA particle performing uniform circular motion has angular momentum `L`. If its angular frequency is double and its kinetic energy halved, then the new angular momentum is :
View SolutionA small ball of radius r rolls down without sliding in a big hemispherical bowl. of radius R. What would be the ratio of the translational and rotational kinetic energies at the bottom of the bowl?
View SolutionA solid iron sphere A rolls down an inclined plane, while another hollow sphere B with the same mass and same radius also rolls down the inclided plane. If `V_(A)` and `V_(B)` are their velocities a the bottom of the inclined plane. Then
A. `V_(A)gtV_(B)`
B. `V_(A)=V_(B)`
C. `V_(A)ltV_(B)`
D. `V_(A)gt = ltV_(B)`
View SolutionA solid sphere and a solid cylinder having the same mass and radius, roil down the same incline. The ratio of their acceleration will be
View SolutionA ring, a disc a sphere and spherical shells are simutaneously released to roll down from the top of an inclined plane of height h. the four bodies will reach the bottom in the following order
View SolutionConsider a wheel of a bicycle rolling on a level road at a linear speed `v_0` figure.

View SolutionStatement 1: A solid sphere and a hollow sphere of same radius and same material are released (at rest ) from the top of a fixed inclined plane at the same time. They will reach the bottom simultaneously, if they roll with sliding.
Statement 2: In the situation of statement 1, the centres of both spheres have the same acceleration and they travel the same distance. Hence time taken is same.
View SolutionStatement-1: if moment of inertia of a rigid body is equal about two axis, then both the axis must be parallel.
Statement-2 from parallel axis theorem `I=I_(cm)+md^(2)`, where all terms have usual meaning.
View SolutionStatement-1 : A thin uniform rod is undergoing fixed axis rotation about one its end with variable angular accleration. Then acceleration vector of any two moving point on the can not be parallel at an instant of time.
Statement-2: for a rod undergoing fixed axis rotation, the velocity of any two moving points on the rod at different distances from centre of rotation are different.
View Solution
Exercise questions and complete solutions for chapter RIGID BODY DYNAMICS of RESONANCE ENGLISH of Class 11