Complete Solutions to Example of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| AAKASH INSTITUTE | Example |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
A uniform magnetic field exists in the space `vecB=B_(1)hati+B_(2)hatj+B_(3)hatk`. Find the magnetic flux through an area `vecS` if the area `vecS` is in (i) x-y plane (ii) y-z plane (iii) z-x plane
View SolutionFigure shows a long straight wire carrying current I and a square conducting wire loop of side l, at a distance 'a' from current wire. Both the current wire and loop are in the plane of paper. Find the flux of magnetic filed of current wire, passing through the loop.

View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA bar magnet is dropped through a horizontal aluminium ring along the axis of the ring. What will be direction of induced current in the loop for the observer shown? What will be the direction of magnetic force experienced by the bar magnet?

View SolutionConsider a coil (of area A, resistance R and number of turns N) held perpendicular to a uniform magnetic field of strength B. The coil is now turned through `180^(@)` in time `Deltat`. What is
(i) Average induced emf
(ii) Average induced current
(iii) Total charge that flows through a given cross-section of the coil?
View SolutionA conducting loop is moving from left to right through a region of uniform magnetic (B) field. Its four positiors are shown belwo. Show the direction of induced current in all four positions.

View SolutionA non uniform magnetic field `B=B_(0)that"i"` in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
View SolutionThrough a uniform B field, A small rectangular loop is moving towards left with constant velocity as shown in the figure. Counting of time t begins at the moment, the loop starts entering the field.
Plot the variation of flux through the loop with respect to time. Also, plot the variation of induced emf w.r.t. time t.

View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity `omega` in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionFigure shows two concentric loops of radii R and `(R gt r)`. A current i is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View SolutionFind the mutual inductance between two coaxial loops of radii R and r (R gtgt r) with separation between the centre x.
View SolutionTwo coaxial coils are very close to each other and their mutual inductance is 5 mH. If a current (50 A) sin 500t is passed in one of the coils, then find the peak value of induced emf in the secondary coil.
View SolutionFind the mutual inductance of two long concentric solenoids for a length l. The area of cross-section of inner solenoid is A and number of turns per unit length are `n_(1)` and `n_(2)`.

View SolutionA uniform magnetic field exists in a circular region of radius R centred at O. The field is perpendicular to the plane of paper and is strength varies with time as `B=B_(0)t`. Find the induced electric field at a distance r from the centre for (i)`r lt R`, (ii) `r gt R`. Also, plot a graph between `|E|` and r for both the cases.
View SolutionProve the energy stored in a current inductor, per unit volume is `(B^(2))/(2mu_(0))`, where B is the magnetic field inside the inductor.
View SolutionCompare the expression for magnetic energy density with electrostatic energy density stored in the space between the plates of a parallel plate capacitor.
View SolutionWhat is the physical role of self inductance?
View SolutionA time varying magnetic field `B=a+bt` exists in a cylindrical region of radius R. A rectangular conducting loop of dimension `Rxx2R` is kept as shown. Find the value of induced EMF in AE, ED and DB ltbegt

View SolutionA line charge `lambda` per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis (Fig. 6.22). A uniform magnetic field extends over a circular region within the rim. It is given by,
`B=B_(0)k" "(ra le a,a lt R)`
=0 `" "` (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off?

View SolutionShows a wire of length l which can slide on a U- shaped rail of negligible resistance. The resistance of the wire is R. The wire is pulled ot the right with a constant speed v. Draw an equivalent circuit diagram representing the induced emf by a battery. Find the current in the wire usingj this diagram.
(##HCV_VOL2_C38_S01_019_Q01##)
(##HCV_VOL2_C38_S01_019_Q02##)
View SolutionFigure shows four conducting rods with end points marked on them. Their dimensions are also mentioned in the figure. Each rod is being moved with a constant velocity v as shown. What is the emf developed between the end points of each rod?

View SolutionAn angle aob made of a conducting wire moves along its bisector through a magnetic field B as suggested by figure. Find the emf induced between the two free ends if the magnetic field is perpendicular ot the plane of the angle.
(##HCV_VOL2_C38_S01_022_Q01##)
(##HCV_VOL2_C38_S01_022_Q02##)
View SolutionA conducting rod AB is bent in the form of a semicircle of radius R. It is kept in a region of uniform magnetic field B such that plane of semicircle is perpendicular to magnetic field. This rod is being moved with a constant speed v perpendicular to AB. Find the emf developed between the ends.
View SolutionA rectangular conducting loop, PQRS is hanging from a thread as shown. Thread is now cut. Compute velocity with which the loop falls as function of time t. Show that if side PS is large enough the loop ultimately falls with constant speed. (m = mass of loop, r = Resistance of loop, PQ = l, PS = b)

View SolutionThe figure shows a part of a complete circuit. At the instant shown, the current `i=2A` and it is decreasing at rate `2xx10^(3)A//s`. Find the potential difference between A and B and energy stored in the magnetic field at this instant. `V_(A)-12+3i+15+5i+L(di)/(dt)+2i=V_(B)`

View SolutionA magnetic flux of `8xx10^(-4)` weber is linked with each turn of a 200 - turn coil when thereis an electric current of 4 A in it. Calculate the self inductance of the coil.
View SolutionTwo coils have self inductances `L_(1)=4 mH and L_(2)=8mH`. Current in both the coils is increasing at same rate. At an instant, when the power given to the two coils is same, find
(i) Ratio of current in the inductors.
(ii) Ratio of potential difference
(iii) Ratio of energy stored
View SolutionIn the Figure shown `i_1=10e^(-2t) A, i_2=4A` and `V_C=3e^(-2t)V`. Determine

a. `i_L` and `V_L` b. `V_(ac), V_(ab), V_(cd)`
View SolutionFigure shows two concentric loops of radii R and `(R gt r)`. A current i is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View SolutionTwo coaxial coils are very close to each other and their mutual inductance is 10 mH. If a current (60 A) sin 500t is passed in one of the coils, then find the peak value of induced emf in the secondary coil.
View SolutionA resistor and inductor are connected in series through a battery. The switch s is closed at time t = 0.

(a) Plot the graph of rate of Joule heating (P) in resistor versus time (t).
(b) Find out the magnitude of current flowing when the rate of increase of magnetic energy in the inductor is maximum.
View SolutionA 20 H inductor is placed in series with 10 W resistor and an emf of 100 V is suddenly applied to the combination. At t = 1 s from t = 1 s from the start, find the rate at which energy is being stored in the magnetic field around the inductor (givne `e^(-0.5)=0.61`).
View SolutionBuble-1 and Bulb-2 shown in the circuit are identical. Key is closed at time t = 0 and after the bulbs start glowing with their full intensities the key is again opened. Comment on the behaviour of the bulbs.
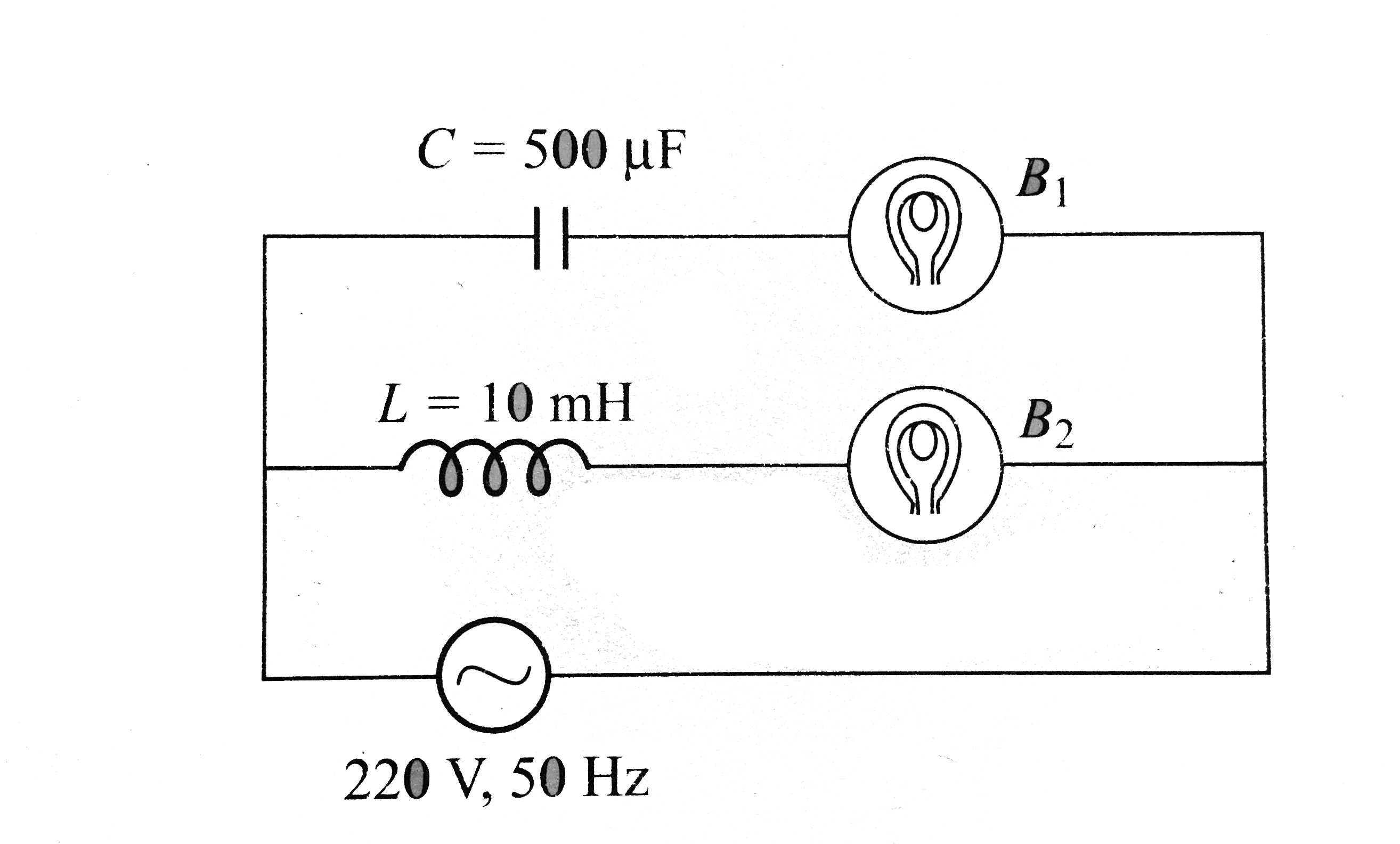
View SolutionA uniform magnetic field exists in the space `vecB=B_(1)hati+B_(2)hatj+B_(3)hatk`. Find the magnetic flux through an area `vecS` if the area `vecS` is in (i) x-y plane (ii) y-z plane (iii) z-x plane
View SolutionFigure shows a long straight wire carrying current , and a square conducting wire loop of side i, at a distance 'a' from current wire. Both the current wire and loop arc in the plane of paper. Find the flux of magnetic field of current wire, passing through the loop.
View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA bar magnet is dropped through a horizontal aluminium ring along the axis of the ring. What will be direction of induced current in the loop for the observer shown? What will be the direction of magnetic force experienced by the bar magnet?

View SolutionConsider a coil (of area A, resistance R and number of turns N) held perpendicular to a uniform magnetic field of strength B. The coil is now turned through `180^(@)` in time `Deltat`. What is
(i) Average induced emf
(ii) Average induced current
(iii) Total charge that flows through a given cross-section of the coil?
View SolutionA conducting loop is moving from left to right through a region of uniform magnetic (B) field. Its four positiors are shown belwo. Show the direction of induced current in all four positions.

View SolutionThere exists a uniform magnetic field `bar B = B_(0)t bar k` in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View SolutionThrough a uniform B field, A small rectangular loop is moving towards left with constant velocity as shown in the figure. Counting of time t begins at the moment, the loop starts entering the field.
Plot the variation of flux through the loop with respect to time. Also, plot the variation of induced emf w.r.t. time t.

View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity `omega` in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
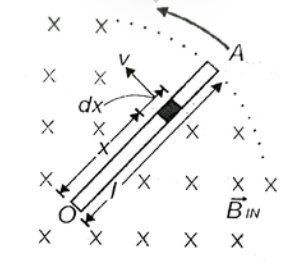
View SolutionA uniform magnetic field exists in a circular region of radius R centred at O. The field is perpendicular to the plane of paper and is strength varies with time as `B=B_(0)t`. Find the induced electric field at a distance r from the centre for (i)`r lt R`, (ii) `r gt R`. Also, plot a graph between `|E|` and r for both the cases.
View SolutionFigure shows two concentric loops of radii R and r (R gtgt r). A current `i` is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View SolutionFind the mutual inductance between two coaxial loops of radii R and r (R >> r) with separation between the centre x.
View SolutionTwo coaxial coils are very close to each other and their mutual inductance is 5 mH. If a current (50 A) sin 500t is passed in one of the coils, then find the peak value of induced emf in the secondary coil.
View SolutionFind the mutual inductance of two long concentric solenoids for a length l. The area of cross-section of inner solenoid is A and number of turns per unit length are `n_(1)` and `n_(2)`.

View SolutionProve the energy stored in a current inductor, per unit volume is `(B^(2))/(2mu_(0))`, where B is the magnetic field inside the inductor.
View SolutionCompare the expression for magnetic energy density with electrostatic energy density stored in the space between the plates of a parallel plate capacitor.
View SolutionWhat is the physical role of self inductance?
View Solution
Example questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Assignment (SECTION - A)
- Assignment (SECTION - B)
- Assignment (SECTION - C)
- Assignment (SECTION - D)
- Assignment (SECTION - E)
- Assignment (SECTION - F)
- Assignment (SECTION - G)
- Assignment (SECTION - H)
- Assignment (SECTION - I)
- Assignment (SECTION - J)
- ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT(SECTION - B) (OBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT(SECTION -C) Previous Years Questions
- ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
- Example
- EXERCISE
- Try Yourself