A resistor and inductor are connected in series through a battery. The switch s is closed at time t = 0.

(a) Plot the graph of rate of Joule heating (P) in resistor versus time (t).
(b) Find out the magnitude of current flowing when the rate of increase of magnetic energy in the inductor is maximum.
Current i at any time t = t is
i=vR(1−e−rtL)
P=i2R=v2R(1−e−RtL)2×R
=v2R(1−e−RtL^(2)
(b) Magnetic energy stored in the inductor
Em=12Li2
Rate of change of magnetic energy
dEmdt=12L(2i)didt=Lididt
(dEmdt)=Pm

Now, dPxdt=ddt(vR)1−e−RtL(vLeRtL)=0
v2LRddt{e−RtL−e2RtL}=0
=v2LR[−RLe−RtL−2RLe−2RTL]=0
⇒ e−Rt'L=12
Current at that time
i=vR(1−e−Rt'L)=vR(1−12)=v2R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
42 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A resistor and inductor are connected in series through a battery.
The switch is closed at time t=0 . Then what is the magnitude of current flowing when rate of increases of magnetic energy in the inductor is maximum
View SolutionA capacitor is charged to a potential of V0. It is connected with an inductor through a switch S. The switch is closed at time t=0. Which of the following statement(s) is/are correct?

View Solution
Knowledge Check
A capacitor is charged to a potential of V0. It is connected with an inductor through a switch S. The switch is closed at time t=0. Which of the following statement(s) is/are correct?
 AThe maximum current in the circuit is V0√CLBPotential across capacitor becomes zero for the first time at t=π√LCCEnergy stored in the inductor at time t=π2√LC is 14CV20DMaximum energy stored in the inductor 12CV20
AThe maximum current in the circuit is V0√CLBPotential across capacitor becomes zero for the first time at t=π√LCCEnergy stored in the inductor at time t=π2√LC is 14CV20DMaximum energy stored in the inductor 12CV20
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
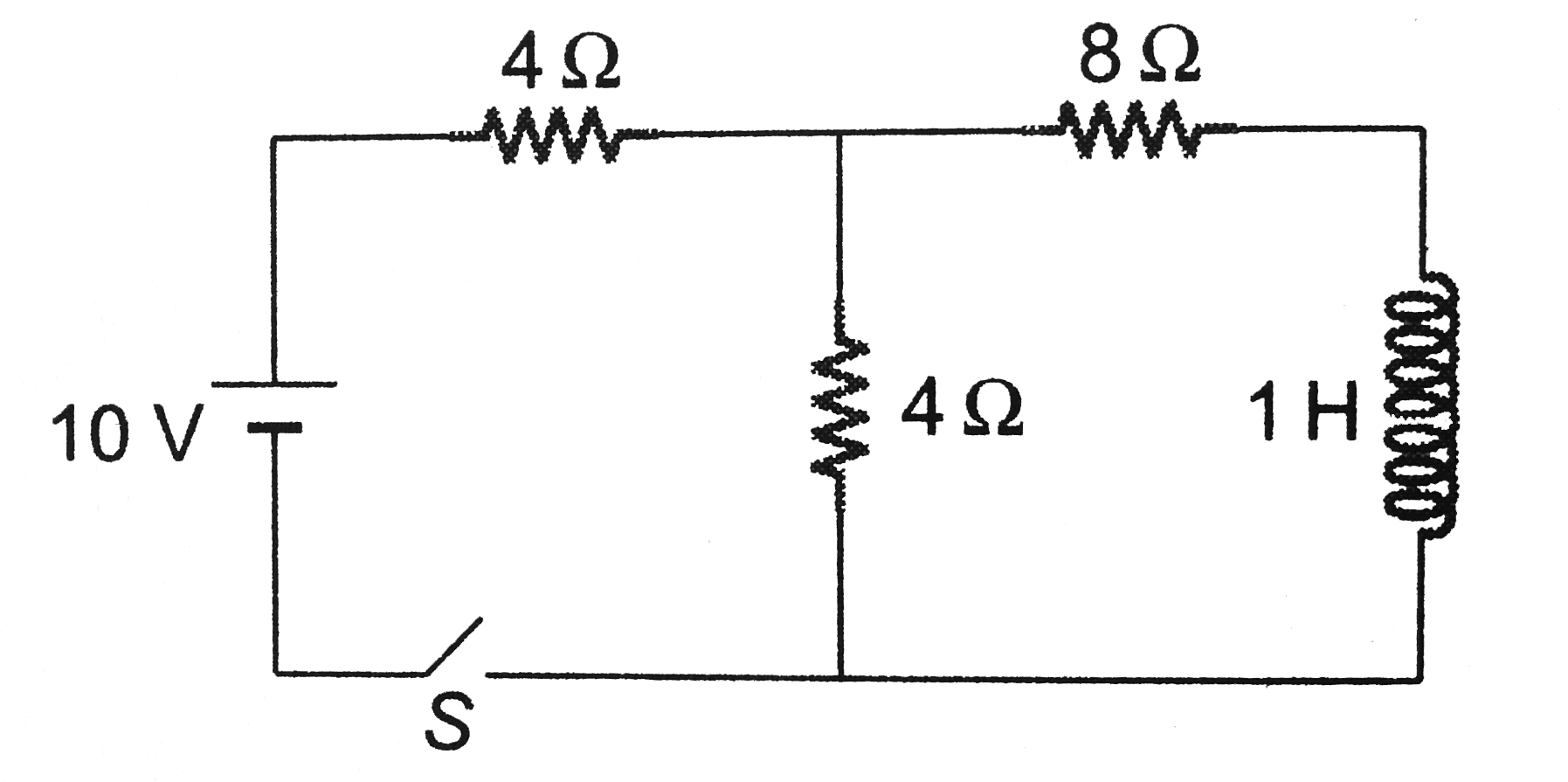
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.

View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

View Solution
