There exists a uniform magnetic field in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
To solve the problem, we need to determine the current flowing through a circular conducting loop placed in a uniform magnetic field that varies with time. Here are the steps to find the current and its direction:
Step 1: Identify the Magnetic Field and Area
The magnetic field is given as ¯B=B0t^k, where B0 is a constant and t is time. The area A of the circular loop with radius r is given by:
A=πr2
Step 2: Calculate the Magnetic Flux
The magnetic flux Φ through the loop is given by the product of the magnetic field and the area of the loop:
Φ=B⋅A=(B0t)⋅(πr2)=B0πr2t
Step 3: Determine the Rate of Change of Magnetic Flux
To find the induced electromotive force (emf), we need to calculate the rate of change of magnetic flux:
dΦdt=ddt(B0πr2t)=B0πr2
Step 4: Apply Faraday's Law of Electromagnetic Induction
According to Faraday's law, the induced emf (E) in the loop is given by:
E=−dΦdt=−B0πr2
Step 5: Calculate the Current through the Loop
Using Ohm's law, the current I through the loop can be calculated as:
I=ER=−B0πr2R
Since current is typically expressed as a positive quantity, we can take the magnitude:
I=B0πr2R
Step 6: Determine the Direction of the Current
According to Lenz's law, the direction of the induced current will be such that it opposes the change in magnetic flux. Since the magnetic flux is increasing in the positive z direction, the induced current will flow in a clockwise direction when viewed from above (in the positive z direction).
Final Answer
The current through the loop is:
I=B0πr2R
And the sense of the current is clockwise.
---
The magnetic field is given as ¯B=B0t^k, where B0 is a constant and t is time. The area A of the circular loop with radius r is given by:
A=πr2
The magnetic flux Φ through the loop is given by the product of the magnetic field and the area of the loop:
Φ=B⋅A=(B0t)⋅(πr2)=B0πr2t
To find the induced electromotive force (emf), we need to calculate the rate of change of magnetic flux:
dΦdt=ddt(B0πr2t)=B0πr2
According to Faraday's law, the induced emf (E) in the loop is given by:
E=−dΦdt=−B0πr2
Using Ohm's law, the current I through the loop can be calculated as:
I=ER=−B0πr2R
Since current is typically expressed as a positive quantity, we can take the magnitude:
I=B0πr2R
According to Lenz's law, the direction of the induced current will be such that it opposes the change in magnetic flux. Since the magnetic flux is increasing in the positive z direction, the induced current will flow in a clockwise direction when viewed from above (in the positive z direction).
The current through the loop is:
I=B0πr2R
And the sense of the current is clockwise.
Similar Questions
A non uniform magnetic field B=B0tˆi in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown
 View Solution
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
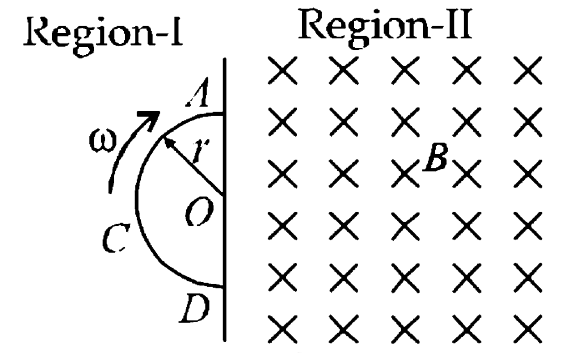
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.

(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.View SolutionA hypthetical magnetic field existing in a region is given by →B=B0→er, where →–––r denotes the uit vector along the redial direction. A circular loop of radus a, carrying a current I, is placed with its plane parallel to the x-y plane and the centre at (0,0, d) .Find the magnitude of the magnetic force acting on the loop.
View SolutionMagnetic field B in a cylindrical region of radius r varies according to the law B=B0t as shown in the figure. A fixed conducting loop ABCDA of resistance R is lying in the region as show . The current flowing through the loop is
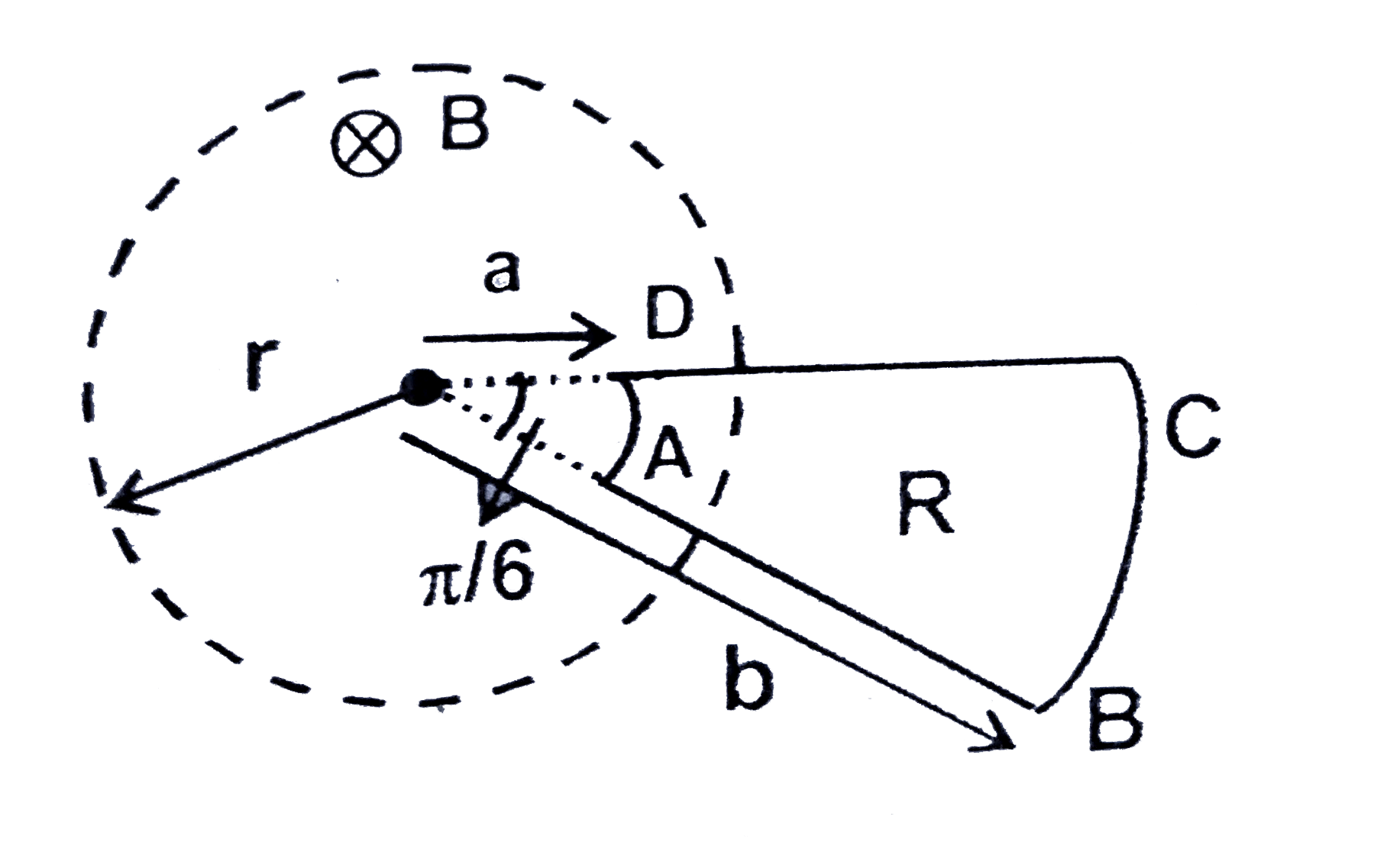 View Solution
View Solution

