Complete Solutions to Exercises Linked Comprehension of chapter CHEMICAL KINETICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETICS |
| CENGAGE CHEMISTRY | Exercises Linked Comprehension |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
The rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every `10^(@)C` rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every `10^(@)C` change in temperature.
`"Temperature coefficient" (mu) = ("Rate constant of" (T + 10)^(@)C)/("Rate constant at" T^(@)C)`
Arrhenius gave an equation which describes aret constant `k` as a function of temperature
`k = Ae^(-E_(a)//RT)`
where `k` is the rate constant, `A` is the frequency factor or pre-exponential factor, `E_(a)` is the activation energy, `T` is the temperature in kelvin, `R` is the universal gas constant.
Equation when expressed in logarithmic form becomes
`log k = log A - (E_(a))/(2.303 RT)`
For a reaction `E_(a) = 0` and `k = 3.2 xx 10^(8)s^(-1)` at `325 K`. The value of `k` at `335 K` would be13:39View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every `10^(@)C` rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every `10^(@)C` change in temperature.
`"Temperature coefficient" (mu) = ("Rate constant of" (T + 10)^(@)C)/("Rate constant at" T^(@)C)`
Arrhenius gave an equation which describes aret constant `k` as a function of temperature
`k = Ae^(-E_(a)//RT)`
where `k` is the rate constant, `A` is the frequency factor or pre-exponential factor, `E_(a)` is the activation energy, `T` is the temperature in kelvin, `R` is the universal gas constant.
Equation when expressed in logarithmic form becomes
`log k = log A - (E_(a))/(2.303 RT)`
For which of the following reactions `k_(310)//k_(300)` would be maximum?13:39View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every `10^(@)C` rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every `10^(@)C` change in temperature.
`"Temperature coefficient" (mu) = ("Rate constant of" (T + 10)^(@)C)/("Rate constant at" T^(@)C)`
Arrhenius gave an equation which describes aret constant `k` as a function of temperature
`k = Ae^(-E_(a)//RT)`
where `k` is the rate constant, `A` is the frequency factor or pre-exponential factor, `E_(a)` is the activation energy, `T` is the temperature in kelvin, `R` is the universal gas constant.
Equation when expressed in logarithmic form becomes
`log k = log A - (E_(a))/(2.303 RT)`
Activation energies of two reaction are `E_(a)` and `E_(a)'` with `E_(a) gt E'_(a)`. If the temperature of the reacting systems is increased form `T_(1)` to `T_(2)` (`k'` is rate constant at higher temperature).13:39View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every `10^(@)C` rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every `10^(@)C` change in temperature.
`"Temperature coefficient" (mu) = ("Rate constant of" (T + 10)^(@)C)/("Rate constant at" T^(@)C)`
Arrhenius gave an equation which describes aret constant `k` as a function of temperature
`k = Ae^(-E_(a)//RT)`
where `k` is the rate constant, `A` is the frequency factor or pre-exponential factor, `E_(a)` is the activation energy, `T` is the temperature in kelvin, `R` is the universal gas constant.
Equation when expressed in logarithmic form becomes
`log k = log A - (E_(a))/(2.303 RT)`
For the given reactions, following data is given
`{:(PrarrQ,,,,k_(1) =10^(15)exp((-2000)/(T))),(CrarrD,,,,k_(2) = 10^(14)exp((-1000)/(T))):}`
Temperature at which `k_(1) = k_(2)` is13:39View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
`log k(s^(-1)) = 14 - (1.25 xx 10^(4) K)/(T)`
Pre-exponential factor for this reaction is11:28View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
`log k(s^(-1)) = 14 - (1.25 xx 10^(4) K)/(T)`
Energy of activation (in `kcal`) is11:28View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
`log k(s^(-1)) = 14 - (1.25 xx 10^(4) K)/(T)`
At what temperature, rate constant is equal to pre-exponential factor?11:28View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
`log k(s^(-1)) = 14 - (1.25 xx 10^(4) K)/(T)`
What is the effect on the rate of reaction at `127^(@)C`, if in the presence of catalyst, energy of activation is lowered by `10 kJ mol^(-1)`?11:28View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
`log k(s^(-1)) = 14 - (1.25 xx 10^(4) K)/(T)`
A two-step mechanism has been suggested for the reaction of nitric oxide and bromine:
`NO(g) + Br_(2)(g) overset(k_(1))rarr NOBr_(2)(g)`
`NOBr_(2)(g)+NO(g) overset(k_(2))rarr 2NOBr(g)`
The observed rate law is, rate `= k[NO]^(2)[Br_(2)]`. Hence, the rate-determining step is11:28View SolutionThe following data were observed for the following reaction at `25^(@)C, CH_(3)OH + (C_(6)H_(5))_(3)C Clrarr(C_(6)H_(5))_(3)C.OCH_(3)+HCl`

Rates `(d[C])/(dt)` in sets I, II, and III are, respectively,
(in `M min^(-1)`):08:36View SolutionThe following data were observed for the following reaction at `25^(@)C, CH_(3)OH + (C_(6)H_(5))_(3)C Clrarr(C_(6)H_(5))_(3)C.OCH_(3)+HCl`

Rate constant of the above experiment is (in `L^(2) M^(-2) min^(-1)`) :08:36View SolutionThe following data were observed for the following reaction at `25^(@)C, CH_(3)OH + (C_(6)H_(5))_(3)C Clrarr(C_(6)H_(5))_(3)C.OCH_(3)+HCl`

Rate law of the above experiment is08:36View SolutionThe energy profile diagram for the reaction:
`CO(g)+NO_(2)(g) hArr CO_(2)(g)+NO(g)` is given below:

The activation energy of the forward reaction is03:04View SolutionThe energy profile diagram for the reaction:
`CO(g)+NO_(2)(g) hArr CO_(2)(g)+NO(g)` is given below:

The activation energy of the backward reaction is03:04View SolutionThe energy profile diagram for the reaction:
`CO(g)+NO_(2)(g) hArr CO_(2)(g)+NO(g)` is given below:
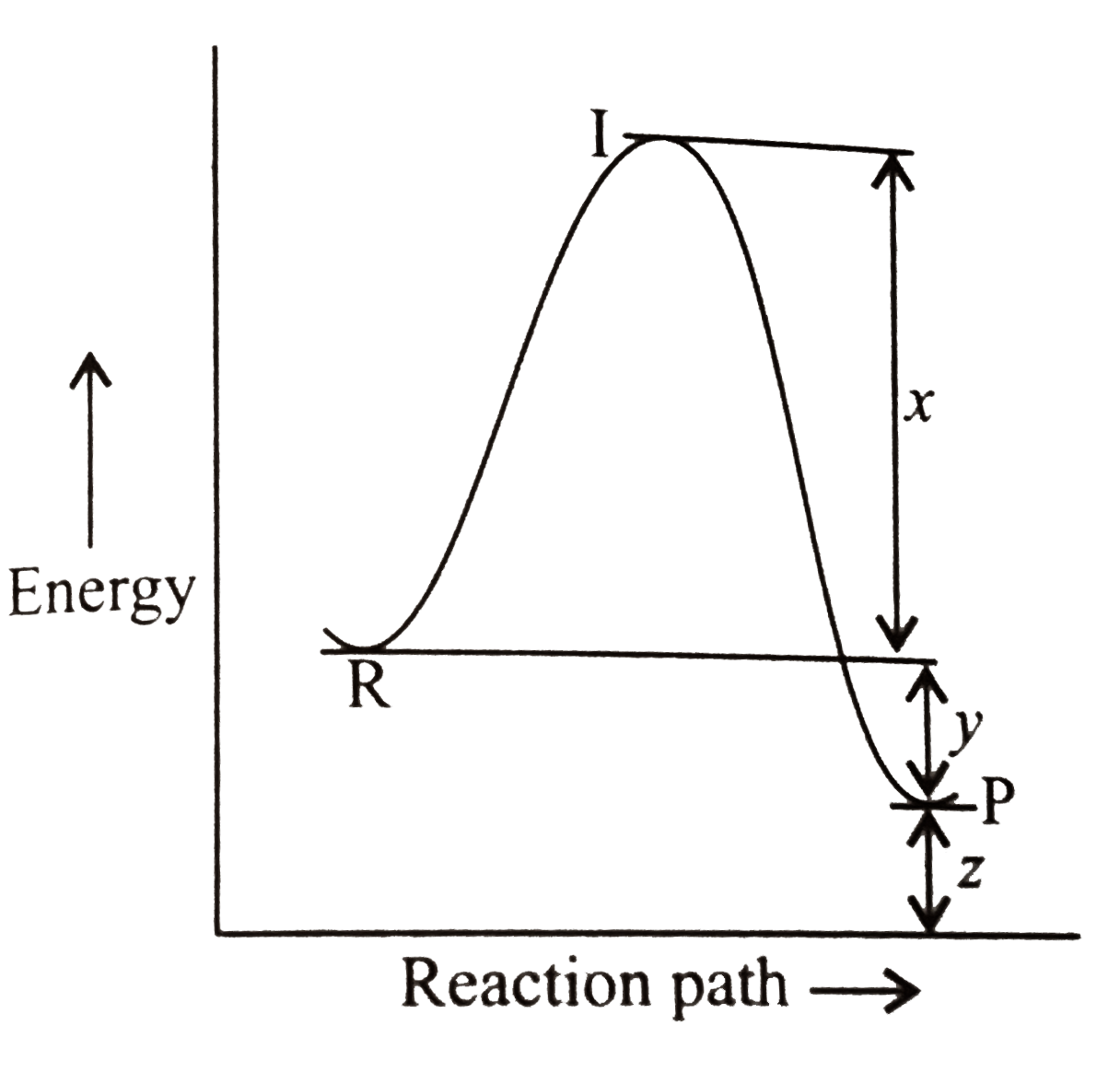
the heat of the reaction is03:04View SolutionThe energy profile diagram for the reaction:
`CO(g)+NO_(2)(g) hArr CO_(2)(g)+NO(g)` is given below:

The threshold energy of the reaction is03:04View SolutionThe reaction `S_(2)O_(8)^(2-) + 3I^(ɵ) rarr 2SO_(4)^(2-) + I_(3)^(ɵ)` is of first order both with respect to persulphate and iofide ions. Taking the initial concentration as `a` and `b`, respectively, and taking `x` as the concentration of the triofide at time `t`, a differential rate equation can be written.
Two suggested mechanism for the reaction are:
I. `S_(2)O_(8)^(2-)+I^(ɵ) hArr SO_(4)I^(ɵ)+SO_(4)^(2-) ("fast")`
`I^(ɵ)+SO_(4)I^(ɵ) overset(k_(1))rarrI_(2) + SO_(4)^(2-)` (show)
`I^(ɵ) + I_(2) overset(k_(2))rarr I_(3)^(ɵ) ("fast")`
II. `S_(2)O_(8)^(2-) + I^(ɵ) overset(k_(1))rarr S_(2)O_(8) I^(2-) (slow)`
`S_(2)O_(8)I^(3-) overset(k_(2))rarr2SO_(4)^(2-)+I^(o+) ("fast")`
`I^(o+) + I^(ɵ) overset(k_(3)) rarr I_(2) ("fast")`
`I_(2) + I^(o+) overset(k_(4))rarr I_(3)^(ɵ) ("fast")`
The general difference equation for the above reaction is06:22View SolutionThe reaction `S_(2)O_(8)^(2-) + 3I^(ɵ) rarr 2SO_(4)^(2-) + I_(3)^(ɵ)` is of first order both with respect to persulphate and iofide ions. Taking the initial concentration as `a` and `b`, respectively, and taking `x` as the concentration of the triofide at time `t`, a differential rate equation can be written.
Two suggested mechanism for the reaction are:
I. `S_(2)O_(8)^(2-)+I^(ɵ) hArr SO_(4)I^(ɵ)+SO_(4)^(2-) ("fast")`
`I^(ɵ)+SO_(4)I^(ɵ) overset(k_(1))rarrI_(2) + SO_(4)^(2-)` (show)
`I^(ɵ) + I_(2) overset(k_(2))rarr I_(3)^(ɵ) ("fast")`
II. `S_(2)O_(8)^(2-) + I^(ɵ) overset(k_(1))rarr S_(2)O_(8) I^(2-) (slow)`
`S_(2)O_(8)I^(3-) overset(k_(2))rarr2SO_(4)^(2-)+I^(o+) ("fast")`
`I^(o+) + I^(ɵ) overset(k_(3)) rarr I_(2) ("fast")`
`I_(2) + I^(o+) overset(k_(4))rarr I_(3)^(ɵ) ("fast")`
For the reaction `I_(2)+2S_(2)O_(3)^(2-) rarr S_(4)O_(6)^(2-) + 2I^(ɵ)`
I. `(-d[I_(2)])/(dt) = -(1)/(2) (d[S_(2)O_(3)^(2-)])/(dt)`
II. `(-d[I_(2)])/(dt) = -2 (d[S_(2)O_(3)^(2-)])/(dt)`
III. `(-d[I_(2)])/(dt) = -2 (d[I^(ɵ)])/(dt) xx (d[S_(2)O_(3)^(2-)])/(dt)`
IV. `(d[S_(4)O_(6)^(2-)])/(dt) = (1)/(2)(d[I^(ɵ)])/(dt)`
The correct option is06:22View SolutionConisder the reaction represented by the equation:
`CH_(3)Cl(g) + H_(2)O(g) rarr CH_(3)OH(g) + HCl(g)`
These kinetics data were obtained for the given reaction concentrations:
`{:("Initial conc (M)",,"Initial rate of disappearance"),([CH_(3)Cl],[H_(2)O],"of "CH_(3)Cl(Ms^(-1))),(0.2,0.2,1),(0.4,0.2,2),(0.4,0.4,8):}`
The rate law for the reaction will be07:28View SolutionConisder the reaction represented by the equation:
`CH_(3)Cl(g) + H_(2)O(g) rarr CH_(3)OH(g) + HCl(g)`
These kinetics data were obtained for the given reaction concentrations:
`{:("Initial conc (M)",,"Initial rate of disappearance"),([CH_(3)Cl],[H_(2)O],"of "CH_(3)Cl(Ms^(-1))),(0.2,0.2,1),(0.4,0.2,2),(0.4,0.4,8):}`
Order with respect to `[CH_(3)Cl]` will be07:28View SolutionConisder the reaction represented by the equation:
`CH_(3)Cl(g) + H_(2)O(g) rarr CH_(3)OH(g) + HCl(g)`
These kinetics data were obtained for the given reaction concentrations:
`{:("Initial conc (M)",,"Initial rate of disappearance"),([CH_(3)Cl],[H_(2)O],"of "CH_(3)Cl(Ms^(-1))),(0.2,0.2,1),(0.4,0.2,2),(0.4,0.4,8):}`
Overall order of the reaction will be07:28View SolutionConisder the reaction represented by the equation:
`CH_(3)Cl(g) + H_(2)O(g) rarr CH_(3)OH(g) + HCl(g)`
These kinetics data were obtained for the given reaction concentrations:
`{:("Initial conc (M)",,"Initial rate of disappearance"),([CH_(3)Cl],[H_(2)O],"of "CH_(3)Cl(Ms^(-1))),(0.2,0.2,1),(0.4,0.2,2),(0.4,0.4,8):}`
Unit of rate constant will be07:28View SolutionConisder the reaction represented by the equation:
`CH_(3)Cl(g) + H_(2)O(g) rarr CH_(3)OH(g) + HCl(g)`
These kinetics data were obtained for the given reaction concentrations:
`{:("Initial conc (M)",,"Initial rate of disappearance"),([CH_(3)Cl],[H_(2)O],"of "CH_(3)Cl(Ms^(-1))),(0.2,0.2,1),(0.4,0.2,2),(0.4,0.4,8):}`
If `H_(2)O` is taken in large excess, the order of the reaction will be07:28View SolutionFor the reaction: `aA + bB rarr cC+dD`
Rate `= (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt)`
For reaction `3BrO^(ɵ) rarr BrO_(3)^(ɵ) + 2Br^(ɵ)`, the value of rate constant at `80^(@)C` in the rate law for `-(d[BrO^(ɵ)])/(dt)` was found to be `0.054 L mol^(-1)s^(-1)`. The rate constant `(k)` for the reaction in terms of `(d[BrO_(3)^(ɵ)])/(dt)` is14:30View SolutionFor the reaction: `aA + bB rarr cC+dD`
Rate `= (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt)`
The rate of formation of `SO_(3)` in the following reaction `2SO_(2) + O_(2) rarr 2SO_(3)` is `100 g min^(-1)`. Hence the rate of disappearance of `O_(2)` is14:30View SolutionFor the reaction: `aA + bB rarr cC+dD`
Rate `= (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt)`
A reaction follows the given concentration-time graph. The rate for this reaction at `20 s` will be
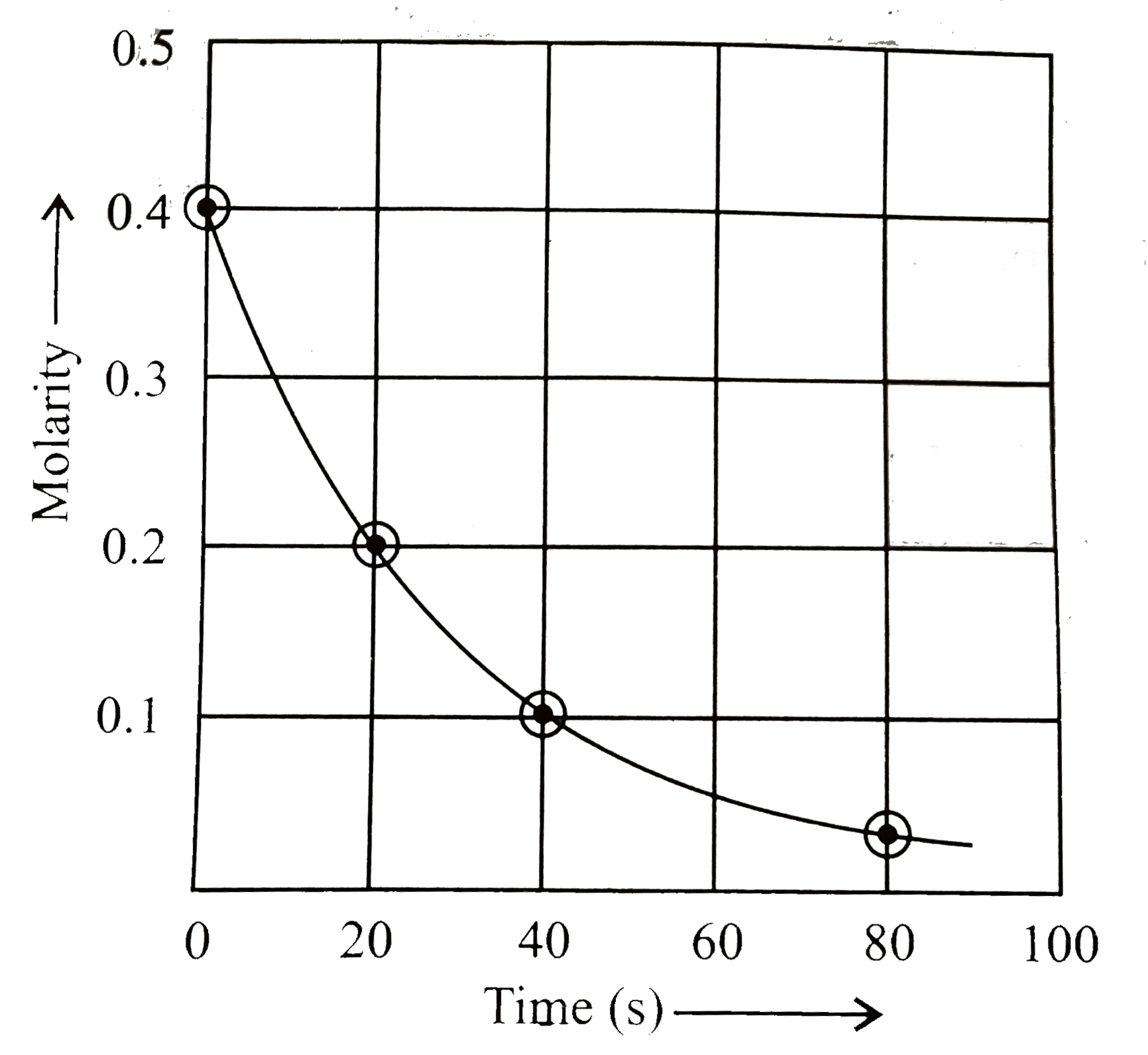 14:30View Solution
14:30View SolutionFor the reaction: `aA + bB rarr cC+dD`
Rate `= (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt)`
In the following reaction,
`xA rarr yB`
`log.[-(d[A])/(dt)] = log.[(d[B])/(dt)] + 0.3`
where negative isgn indicates rate of disappearance of the reactant. Thus, `x:y` is:14:30View SolutionThe energy change accompanying the equilibrium reaction `A hArr B` is `-33.0 kJ mol^(-1)`.
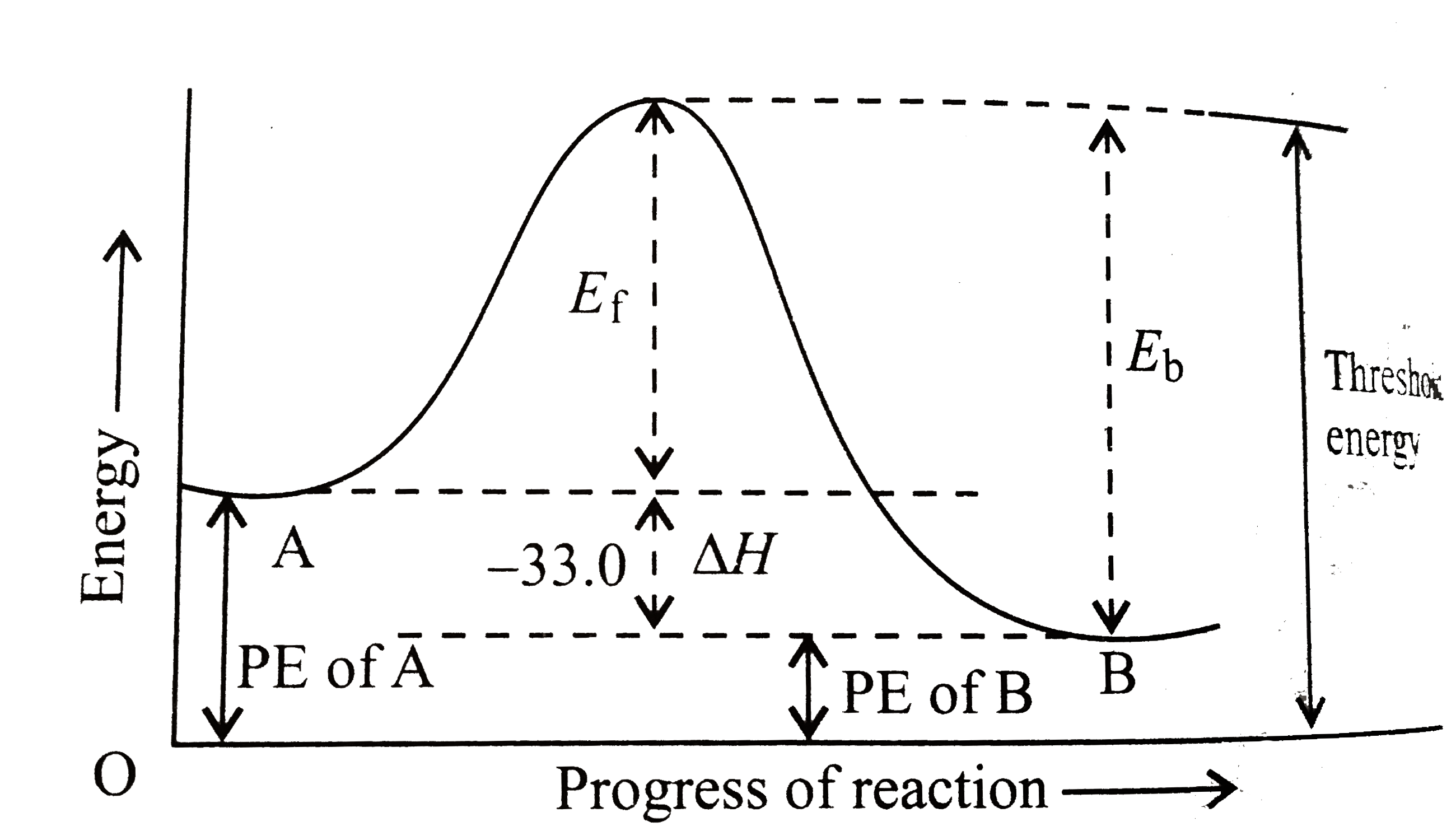
Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The equilibrium constant `k` for the reaction at `300 K`07:07View SolutionThe energy change accompanying the equilibrium reaction `A hArr B` is `-33.0 kJ mol^(-1)`.

Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The energy of activation for forward and backward reactions (`E_(f)` and `E_(b)`) at `300 K`. Given that `E_(f)` and `E_(b)` are in the ratio `20 : 31`,07:07View SolutionThe energy change accompanying the equilibrium reaction `A hArr B` is `-33.0 kJ mol^(-1)`.
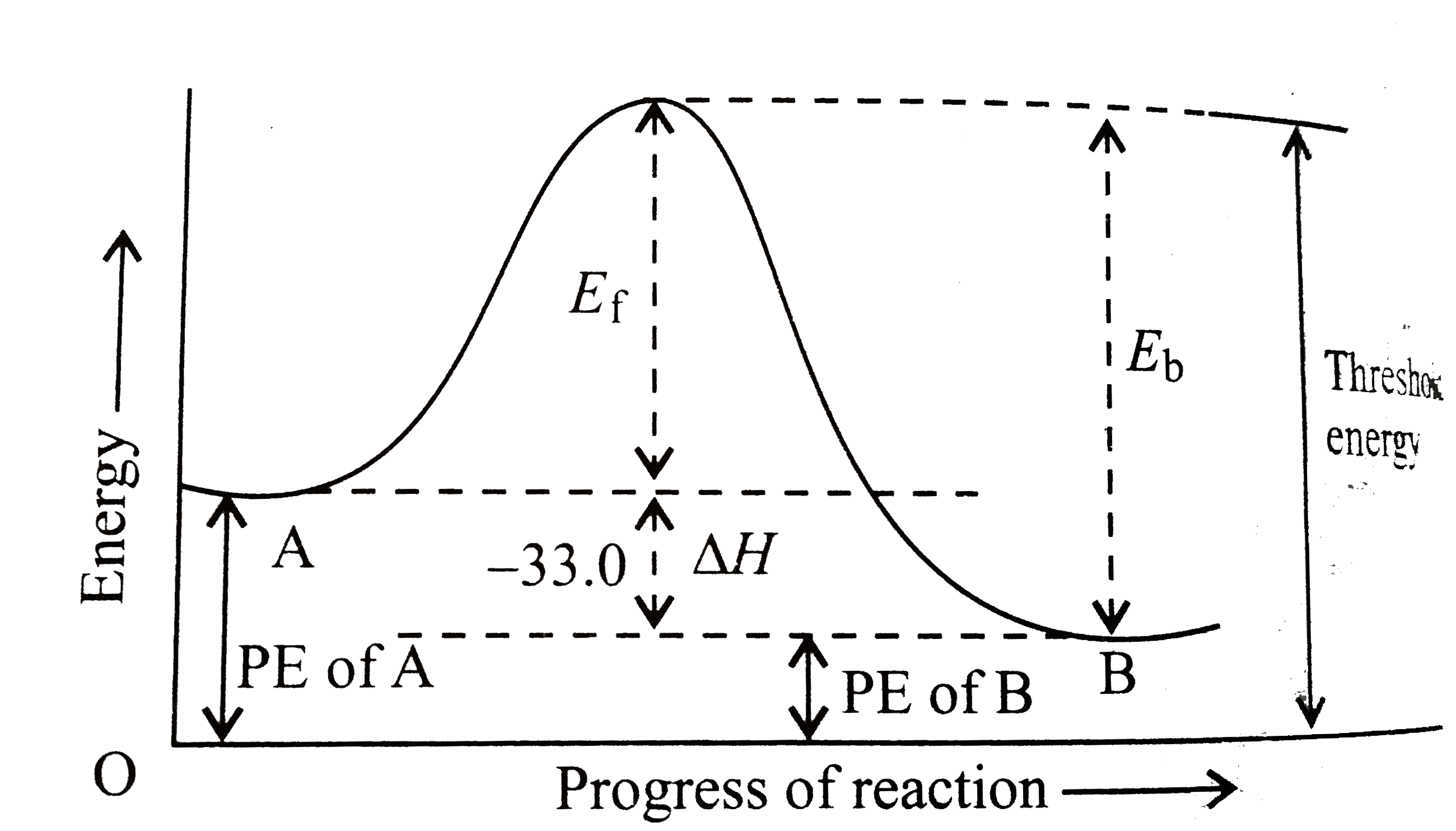
Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The threshold energy of the reaction is when `PE` of `B` is `30 kJ mol^(-1)`.07:07View SolutionIn the start of summer, a given sample of milk turns sour at room temperature `(27^(@)C)` in `48` hours. In a refrigerator at `2^(@)C`, milk can be stored there times longer before it sours.
The activation energy of the souring of milk is `(kJ mol^(-1))`08:30View SolutionIn the start of summer, a given sample of milk turns sour at room temperature `(27^(@)C)` in `48` hours. In a refrigerator at `2^(@)C`, milk can be stored there times longer before it sours.
The time taken by the milk to sour at `37^(@)C`08:30View SolutionIn the start of summer, a given sample of milk turns sour at room temperature `(27^(@)C)` in `48` hours. In a refrigerator at `2^(@)C`, milk can be stored there times longer before it sours.
Calculate the rate constant at `310 K`, when rate constant at `300 K` is `1.6 xx 10^(5)`08:30View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy `E_(a)` Large the value of activation energy, smaller the value of rate constant `k`. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant `k`.
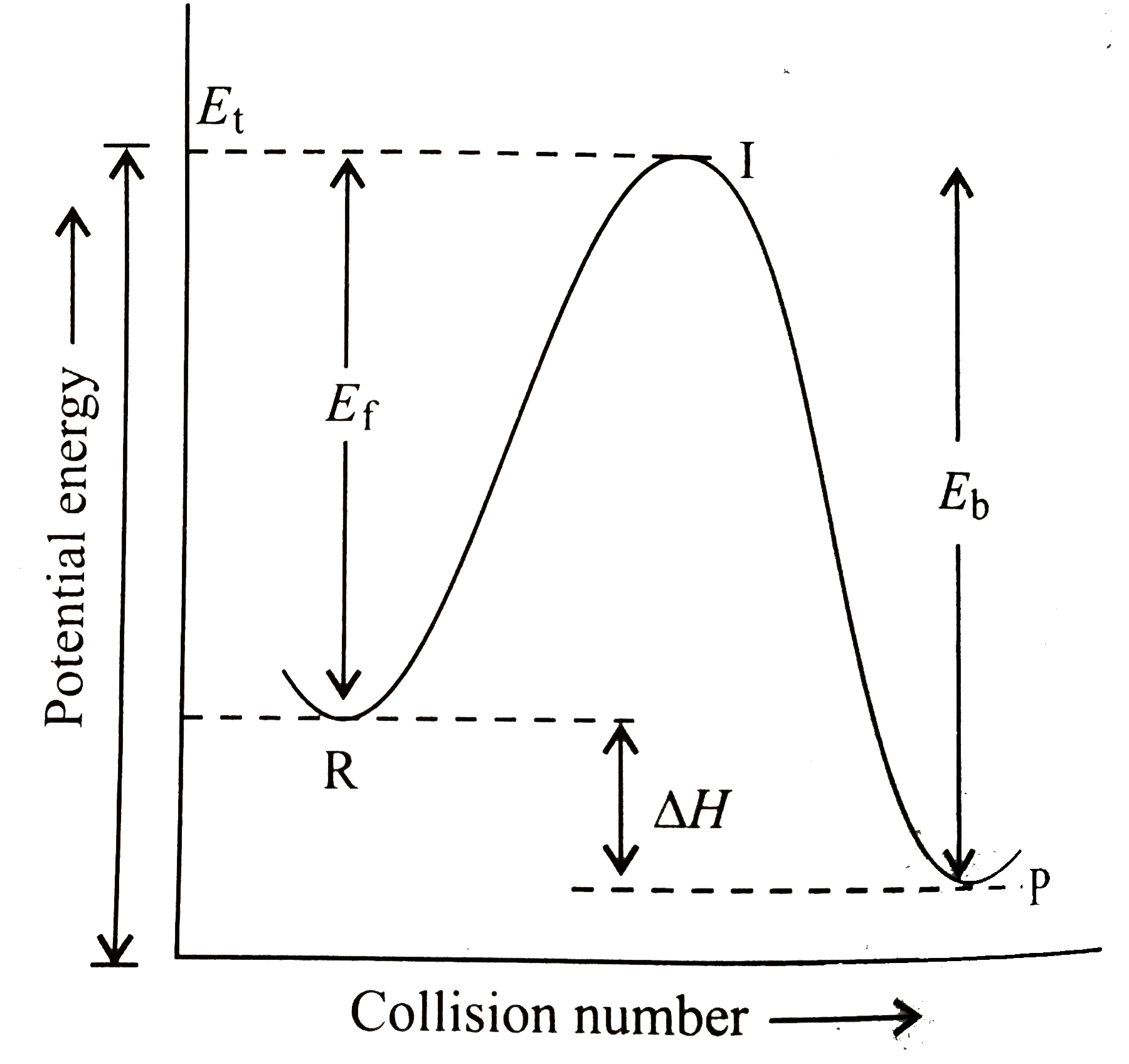
`E_(f) =` Activation energy of forward reaction
`E_(b) =` Activation energy of backward reaction
`Delta H = E_(f) - E_(b)`
`E_(f) =` threshold energy
If a reaction `A + B rarr C` is exothermic to the extent `30 kJ mol^(-1)` and the forward reaction has an activation energy of `249 kJ mol^(-1)` the activation energy for reverse reaction in `kJ mol^(-1)` is10:29View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy `E_(a)` Large the value of activation energy, smaller the value of rate constant `k`. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant `k`.
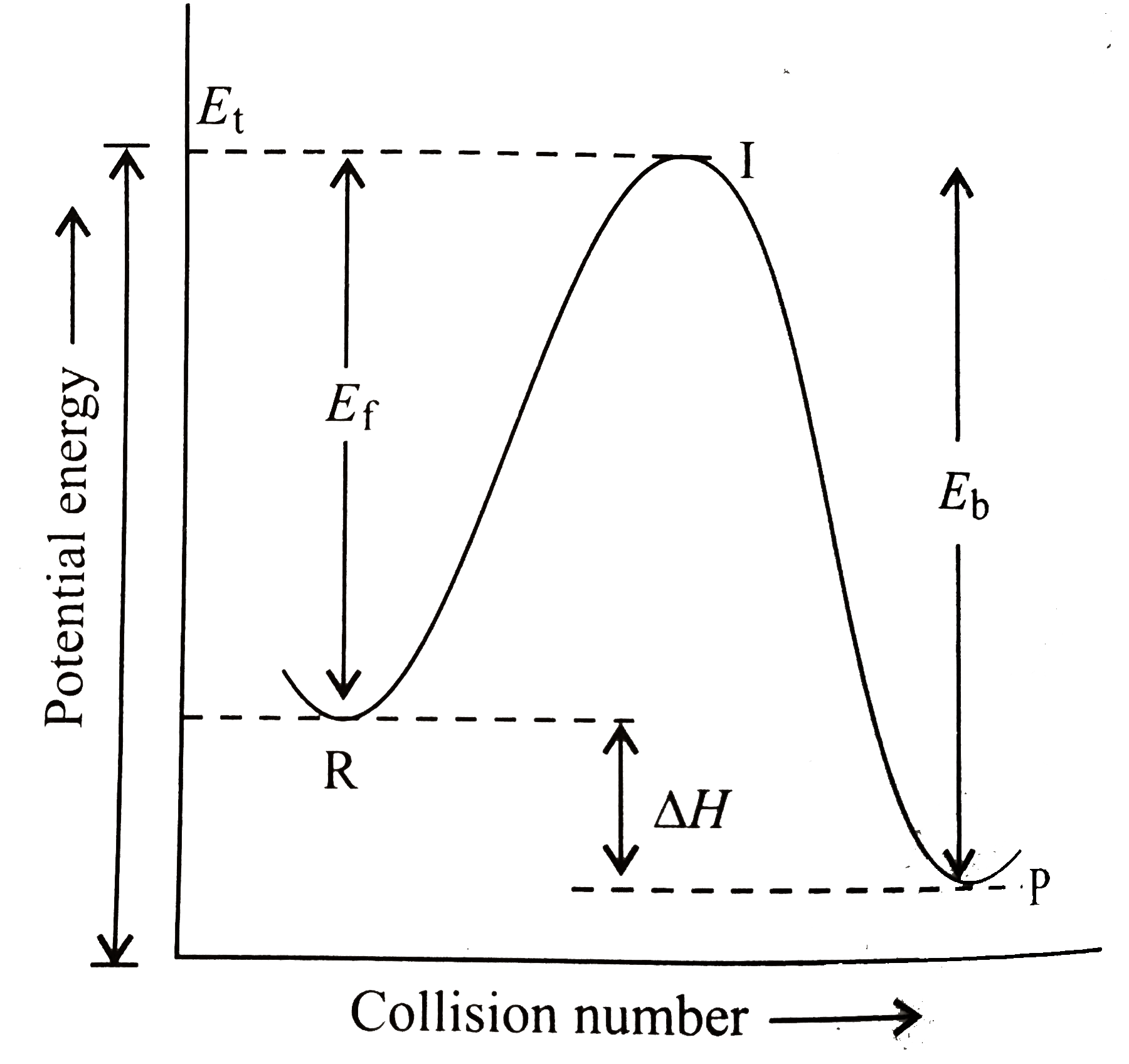
`E_(f) =` Activation energy of forward reaction
`E_(b) =` Activation energy of backward reaction
`Delta H = E_(f) - E_(b)`
`E_(f) =` threshold energy
For the following reaction at a particular temperature, according to the equations
`2N_(2)O_(5) rarr 4NO_(2)+O_(2)`
`2NO_(2) + (1)/(2)O_(2) rarr N_(2)O_(5)`
The activation energies are `E_(1)` and `E_(2)`, respectively. Then10:29View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy `E_(a)` Large the value of activation energy, smaller the value of rate constant `k`. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant `k`.

`E_(f) =` Activation energy of forward reaction
`E_(b) =` Activation energy of backward reaction
`Delta H = E_(f) - E_(b)`
`E_(f) =` threshold energy
In a hypothetical reaction `A rarr B`, the activation energies for the forward and backward reactions are `15` and `9 kJ mol^(-1)`, respectively. The potential energy of `A` is `10 kJ mol^(-1)`. Which of the following is wrong?10:29View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy `E_(a)` Large the value of activation energy, smaller the value of rate constant `k`. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant `k`.
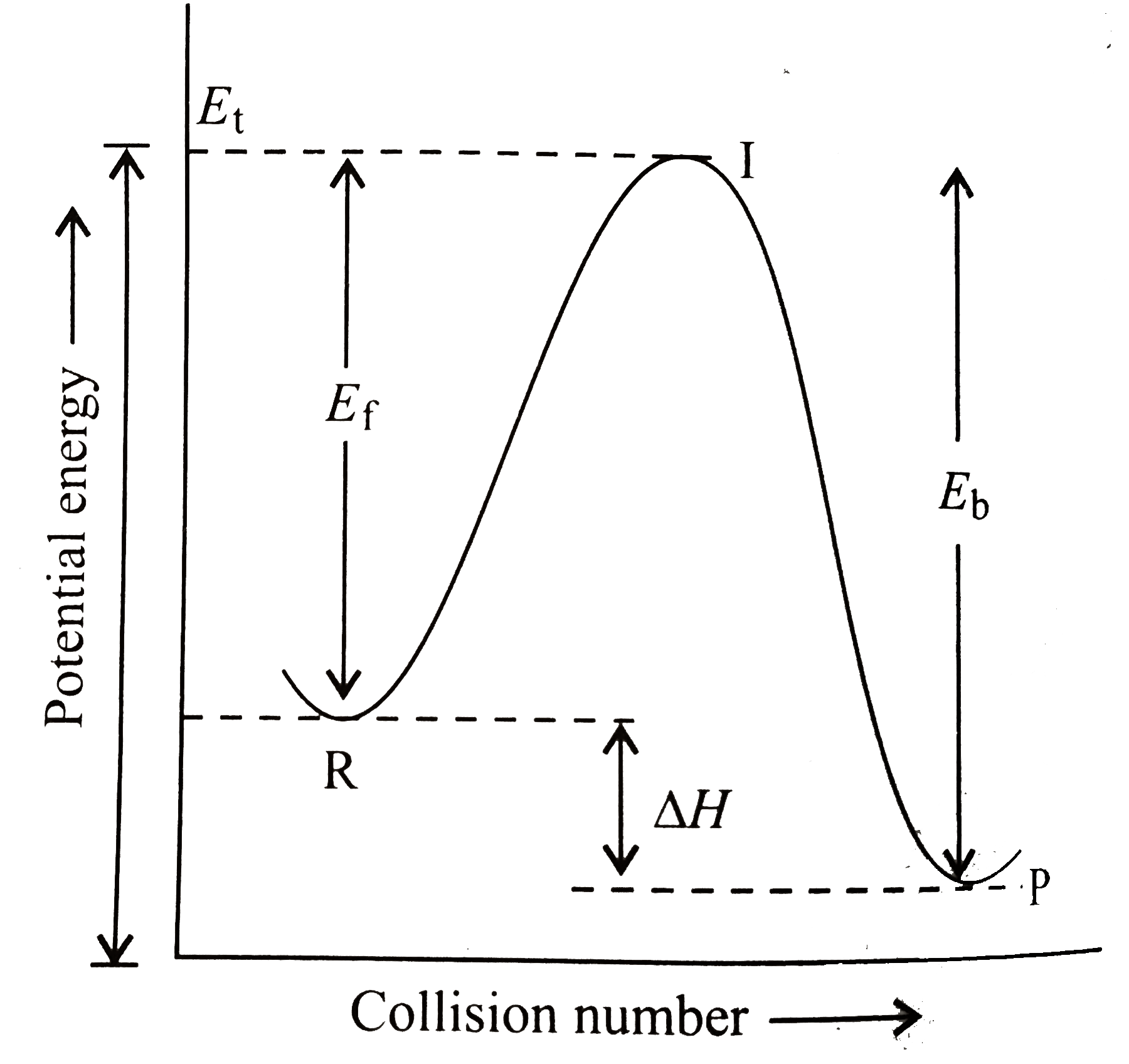
`E_(f) =` Activation energy of forward reaction
`E_(b) =` Activation energy of backward reaction
`Delta H = E_(f) - E_(b)`
`E_(f) =` threshold energy
For two reactions, activation energies are `E_(a1)` and `E_(a2)`, rate constant are `k_(1)` and `k_(2)` at the same temperature. If `k_(1) gt k_(2)`, then10:29View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy `E_(a)` Large the value of activation energy, smaller the value of rate constant `k`. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant `k`.
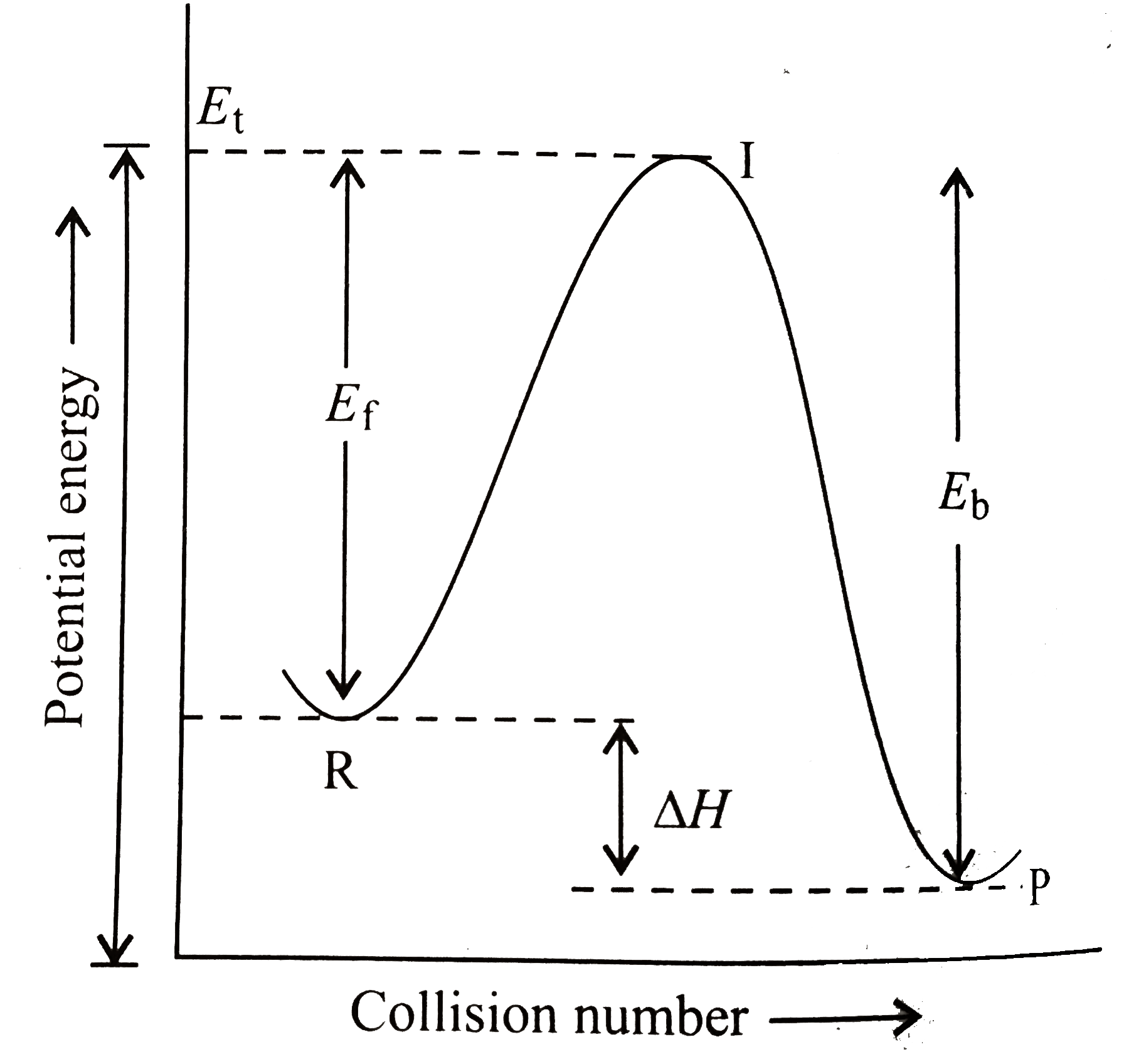
`E_(f) =` Activation energy of forward reaction
`E_(b) =` Activation energy of backward reaction
`Delta H = E_(f) - E_(b)`
`E_(f) =` threshold energy
The rate constant of a certain reaction is given by `k = Ae^(-E_(a)//RT)`
(where `A =` Arrhenius constant). Which factor should be lowered so that the rate of reaction may increase?10:29View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy `E_(a)` Large the value of activation energy, smaller the value of rate constant `k`. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant `k`.

`E_(f) =` Activation energy of forward reaction
`E_(b) =` Activation energy of backward reaction
`Delta H = E_(f) - E_(b)`
`E_(f) =` threshold energy
The activation eneries for forward and backward reactions in a chemical reaction are `30.5` and `45.4 kJ mol^(-1)` respectively. The reaction is10:29View SolutionThe order of reaction is an experimentally determined quanity. It may be zero, poistive, negative, or fractional. The kinetic equation of `nth` order reaction is
`k xx t = (1)/((n-1))[(1)/((a-x)^(n-1)) - (1)/(a^(n-1))]` …(i)
Half life of `nth` order reaction depends on the initial concentration according to the following relation:
`t_(1//2) prop (1)/(a^(n-1))` ...(ii)
The unit of the rate constant varies with the order but general relation for the unit of `nth` order reaction is
Units of `k = [(1)/(Conc)]^(n-1) xx "Time"^(-1)` ...(iii)
The differential rate law for `nth` order reaction may be given as:
`(dX)/(dt) = k[A]^(n)` ...(iv)
where `A` denotes the reactant.
The unit of rate and rate constant are same for09:27View SolutionThe order of reaction is an experimentally determined quanity. It may be zero, poistive, negative, or fractional. The kinetic equation of `nth` order reaction is
`k xx t = (1)/((n-1))[(1)/((a-x)^(n-1)) - (1)/(a^(n-1))]` …(i)
Half life of `nth` order reaction depends on the initial concentration according to the following relation:
`t_(1//2) prop (1)/(a^(n-1))` ...(ii)
The unit of the rate constant varies with the order but general relation for the unit of `nth` order reaction is
Units of `k = [(1)/(Conc)]^(n-1) xx "Time"^(-1)` ...(iii)
The differential rate law for `nth` order reaction may be given as:
`(dX)/(dt) = k[A]^(n)` ...(iv)
where `A` denotes the reactant.
The rate constant for zero order reaction is
where `c_(0)` and `c_(t)` are concentration of reactants at respective times.09:27View SolutionThe order of reaction is an experimentally determined quanity. It may be zero, poistive, negative, or fractional. The kinetic equation of `nth` order reaction is
`k xx t = (1)/((n-1))[(1)/((a-x)^(n-1)) - (1)/(a^(n-1))]` …(i)
Half life of `nth` order reaction depends on the initial concentration according to the following relation:
`t_(1//2) prop (1)/(a^(n-1))` ...(ii)
The unit of the rate constant varies with the order but general relation for the unit of `nth` order reaction is
Units of `k = [(1)/(Conc)]^(n-1) xx "Time"^(-1)` ...(iii)
The differential rate law for `nth` order reaction may be given as:
`(dX)/(dt) = k[A]^(n)` ...(iv)
where `A` denotes the reactant.
The half life for a zero order reaction equals09:27View SolutionThe order of reaction is an experimentally determined quanity. It may be zero, poistive, negative, or fractional. The kinetic equation of `nth` order reaction is
`k xx t = (1)/((n-1))[(1)/((a-x)^(n-1)) - (1)/(a^(n-1))]` …(i)
Half life of `nth` order reaction depends on the initial concentration according to the following relation:
`t_(1//2) prop (1)/(a^(n-1))` ...(ii)
The unit of the rate constant varies with the order but general relation for the unit of `nth` order reaction is
Units of `k = [(1)/(Conc)]^(n-1) xx "Time"^(-1)` ...(iii)
The differential rate law for `nth` order reaction may be given as:
`(dx)/(dt) = k[A]^(n)` ...(iv)
where `A` denotes the reactant.
For a reaction:
`I^(ɵ) + OCl^(ɵ) rarr IO^(ɵ) + Cl^(ɵ)`
in an aqueous medium, the rate of the reaction is given by
`(d[IO^(ɵ)])/(dt) = k([I^(ɵ)][OCl^(ɵ)])/([overset(ɵ)(OH)])`
The overall order of the reaction is09:27View SolutionThe order of reaction is an experimentally determined quanity. It may be zero, poistive, negative, or fractional. The kinetic equation of `nth` order reaction is
`k xx t = (1)/((n-1))[(1)/((a-x)^(n-1)) - (1)/(a^(n-1))]` …(i)
Half life of `nth` order reaction depends on the initial concentration according to the following relation:
`t_(1//2) prop (1)/(a^(n-1))` ...(ii)
The unit of the rate constant varies with the order but general relation for the unit of `nth` order reaction is
Units of `k = [(1)/(Conc)]^(n-1) xx "Time"^(-1)` ...(iii)
The differential rate law for `nth` order reaction may be given as:
`(dx)/(dt) = k[A]^(n)` ...(iv)
where `A` denotes the reactant.
In a chemical reaction `A rarr B`, it is found that the rate of the reaction doubles when the concentration of `A` is increased four times. The order of the reaction with respect to `A` is:09:27View SolutionConisder the following elementary reaction,
`2A + B + C rarr` Products. All reactants are present in the gaseous state and reactant `C` is taken in excess.
What is the rate expresison of the reaction?02:14View SolutionConisder the following elementary reaction,
`2A + B + C rarr` Products. All reactants are present in the gaseous state and reactant `C` is taken in excess.
What is the unit of rate constant of the reaction?02:45View SolutionConisder the following elementary reaction,
`2A + B + C rarr` Products. All reactants are present in the gaseous state and reactant `C` is taken in excess.
How will the rate change if the concentration of A is doubled and that of B is tripled ?04:00View SolutionFor the reaction: `X(g) rarr Y(g)+Z(g)`, the following data were obtained at `30^(@)C`:
`{:("Experiment",[X](mol L^(-1)),"Rate" (mol L^(-1) hr^(-1))),(I,0.17,0.05),(II,0.34,0.10),(III,0.68,0.20):}`
The rate constant of the above reaction is03:33View SolutionFor the reaction: `X(g) rarr Y(g)+Z(g)`, the following data were obtained at `30^(@)C`:
`{:("Experiment",[X](mol L^(-1)),"Rate" (mol L^(-1) hr^(-1))),(I,0.17,0.05),(II,0.34,0.10),(III,0.68,0.20):}`
The equilibrium constant for the reaction is `0.50`. Assuming that the reaction proceeds by one-step mechanism. Find the rate constant of reverse reaction?04:57View SolutionFor the reaction: `X(g) rarr Y(g)+Z(g)`, the following data were obtained at `30^(@)C`:
`{:("Experiment",[X](mol L^(-1)),"Rate" (mol L^(-1) hr^(-1))),(I,0.17,0.05),(II,0.34,0.10),(III,0.68,0.20):}`
In experiment `(I)`, what time will reactant `(X)` take to be reduced into `0.0425 M`?06:52View SolutionThe reaction `2AX(g)+2B_(2)(g)rarr A_(2)(g)+2B_(2)X(g)` has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. `2A X hArr A_(2)X_(2) " " ("fast and reverse")`
II. `A_(2)X_(2)+B_(2)rarrA_(2)X+B_(2)X`
III. `A_(2)X+B_(2)rarrA_(2)+B_(2)X`
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
Let the equilibrium constant of Step I be `2xx10^(-3) mol^(-1) L` and the rate constants for the formation of `A_(2)X` and `A_(2)` in Step II and III are `3.0xx10^(-2) mol^(-1) L min^(-1)` and `1xx10^(3) mol^(-1) L min^(-1)` (all data at `25^(@)C)`, then what is the overall rate constant `(mol^(-2) L^(2) min^(-1))` of the consumption of `B_(2)`?09:32View SolutionThe reaction `2AX(g)+2B_(2)(g)rarr A_(2)(g)+2B_(2)X(g)` has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. `2A X hArr A_(2)X_(2) " " ("fast and reverse")`
II. `A_(2)X_(2)+B_(2)rarrA_(2)X+B_(2)X`
III. `A_(2)X+B_(2)rarrA_(2)+B_(2)X`
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
How many times the rate of formation of `A_(2)` will increase if concentrations of `AX` is doubled and that of `B_(2)` is increased theee fold?09:32View SolutionThe reaction `2AX(g)+2B_(2)(g)rarr A_(2)(g)+2B_(2)X(g)` has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. `2A X hArr A_(2)X_(2) " " ("fast and reverse")`
II. `A_(2)X_(2)+B_(2)rarrA_(2)X+B_(2)X`
III. `A_(2)X+B_(2)rarrA_(2)+B_(2)X`
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
What is the initial rate of formation of `A_(2)` when `[AX]=0.1M` and `[B_(2)]=1.0M`09:32View SolutionThe rate law expresison is given for a typical reaction, `n_(1)A + n_(2) B rarrP` as `r = k[A]^(n)[B]^(n2)`. The reaction completes only in one step and `A` and `B` are present in the solution. If the reaction occurs in more than one step, then the rate law is expressed by consdering the slowest step, i.e., for `S_(N)l` reaction `r = k[RX]`. If the eraction occurs in more than one step and the rates of the steps involved are comparable, then steady state approximation is conisdered, i.e., the rate of formation of intermediate is always equal to the rate of decompoistion of the intermediate. Conisder the reaction:
`[[I_(2) underset(k_(1))overset(k_(2))hArr2I("rapid equilibrium")],[H_(2)+2I overset(k_(3))rarr 2HI("slow")]]`
If we increase the concentration of `I_(2)` two times, then the rate of formation of `HI` will05:04View SolutionThe rate law expresison is given for a typical reaction, `n_(1)A + n_(2) B rarrP` as `r = k[A]^(n)[B]^(n2)`. The reaction completes only in one step and `A` and `B` are present in the solution. If the reaction occurs in more than one step, then the rate law is expressed by consdering the slowest step, i.e., for `S_(N)l` reaction `r = k[RX]`. If the eraction occurs in more than one step and the rates of the steps involved are comparable, then steady state approximation is conisdered, i.e., the rate of formation of intermediate is always equal to the rate of decompoistion of the intermediate. Conisder the reaction:
`[[I_(2) underset(k_(1))overset(k_(2))hArr2I("rapid equilibrium")],[H_(2)+2I overset(k_(3))rarr 2HI("slow")]]`
Which of the following expresison is correct?05:04View SolutionA secondary alkyl halide `(A)` hydrolyzes with alkali `(B)` in aqueous medium ismultaneously via `S_(N)1` and `S_(N)2` pathways with rate constants `k_(1)` and `k_(2)`, respectively. form kinetic data, it was found that a plot of `= (-1)/([A])(d[A])/(dt)` vs `[B]` is straight line with a slope equal to `2.7 xx 10^(-4) L mol^(-1) min^(-1)` and intercept equal to `1.02 xx 10^(-3)`. Minimum initial concentration of `[A] = 0.2 M` and `[B]`, i.e., `[overset(ɵ)(OH)] = 0.5 M`.
The value of overall rate constant of the hydrolyiss of `A` (in `L mol^(-1) min^(-1))` is07:17View SolutionA secondary alkyl halide `(A)` hydrolyzes with alkali `(B)` in aqueous medium ismultaneously via `S_(N)1` and `S_(N)2` pathways with rate constants `k_(1)` and `k_(2)`, respectively. form kinetic data, it was found that a plot of `= (-1)/([A])(d[A])/(dt)` vs `[B]` is straight line with a slope equal to `2.7 xx 10^(-4) L mol^(-1) min^(-1)` and intercept equal to `1.02 xx 10^(-3)`. Minimum initial concentration of `[A] = 0.2 M` and `[B]`, i.e., `[overset(ɵ)(OH)] = 0.5 M`.
The initial rate of consumption is isopropyl chloride (in `M min^(-1))` is07:17View SolutionIf a unimolecular reaction, `A(g) rarr` Products, takes place according to the mechanism
I. `A+A underset(k_(-1))overset(k_(1))hArr A^(**)+A`
II. `A^(**)underset(k_(2))rarr P`
where `k_(1), k_(-1)`, and `k_(2)` are the rate constant and `P, A`, and `A^(**)` stand for Product molecule, normal molecules of reactants and activated molecules of reactants respectively.
Which of the following expresison are correct?08:38View SolutionIf a unimolecular reaction, `A(g) rarr` Products, takes place according to the mechanism
I. `A+A underset(k_(-1))overset(k_(1))hArr A^(**)+A`
II. `A^(**)underset(k_(2))rarr P`
where `k_(1), k_(-1)`, and `k_(2)` are the rate constant and `P, A`, and `A^(**)` stand for Product molecule, normal molecules of reactants and activated molecules of reactants respectively.
Which of the following statements are correct ?08:38View Solution
Exercises Linked Comprehension questions and complete solutions for chapter CHEMICAL KINETICS of CENGAGE CHEMISTRY (HINGLISH) of Class 12
All Exercises from CENGAGE CHEMISTRY Class 12 CHEMISTRY CHEMICAL KINETICS
- Archives Fill In The Blanks
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives Subjective
- Archives True/False
- Ex 4.1 (Objective)
- Ex 4.2 (Objective)
- Ex 4.3 (Objective)
- Ex 4.3 More Than One Correct
- Ex4.4 Objective
- Exercises Assertion-Reasoning
- Exercises Fill In The Blanks
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises True/False
- Illustration
- Solved Example
