Complete Solutions to Solved Example of chapter CHEMICAL KINETICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | CHEMICAL KINETICS |
| CENGAGE CHEMISTRY | Solved Example |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
Which of the following will react fastest (i.e., profuce most of the Product in a given time) and which will react at the highest rate?
(a) `1 mol` of `A` and `1 mol` of `B` in a `1-L` vessel.
(b) `2 mol` of `A` and `2 mol` of `B` in a `2-L` vessel.
( c) `0.2 mol` of `A` and `0.2 mol` of `B` in a `0.1-L` vessel.02:27View SolutionFor the reaction,
`2N_(2)O_(5) (g) rarr 4NO_(2)(g) + O_(2)(g)`, the rate of formation of `O_(2)` is `0.032 g h^(-1)`.
(a) Calculate the rate of converison of `N_(2)O_(5)` in `g h^(-1)`.
(b) Calculate the rate of formation of `NO_(2)` in `g h^(-1)`.04:21View SolutionThe rate of formation of a dimer in a second order dimerization reaction is `9.5 xx 10^(-5) mol L^(-1) s^(-1)` at `0.01 mol L^(-1)` monomer concentration. Calculate the rate constant.
02:02View SolutionFor the decompoistion of phosphorus pentachloride at `200^(@)C`, it is observed that its pressure falls form `0.15` to `0.10 atm` in `25 min`. Calculate the average rate of reaction in
(a) `atm min^(-1)` , (b) `mol L^(-1) s^(-1)`03:50View SolutionRaiisng the concentration of a particular reactant by a factor of `5` increases the reaction rate `25` times. What is the kinetic order of this reactant?
01:37View SolutionThe rate of reaction:
`H_(2)O + 2S_(2)O_(4)^(2-)(aq) rarr 2HSO_(3)^(ɵ)(aq) + S_(2)O_(3)^(2-)(aq)`
was studied as follows. In an experiment, the concentration of `S_(2)O_(4)^(2-)(0.4 M)` half changed in `3.73 xx 10^(6) s`. In another experiment, `0.25 M S_(2)O_(4)^(2-)` half changed in `6.0 xx 10^(6) s`. Find the order of the reaction.03:22View SolutionThe experiment data for the decompoistion of nitrogen pentoxide in the gaseous phase at `218 K` are as follows: `2N_(2)O_(5)(g) rarr 4NO_(2)(g) + O_(2)(g)`

Calculating the rates of reaction at the time given above (assuming that the rate remains constant during the intervals given). Also find the out the following:
(a) Rate law expresison
(b) Rate constant
(c ) Order of reaction05:28View SolutionThe following rate data were obtained at `303 K` for the following reaction:
`2A + B rarr C + D`

What is the rate law? What is the order with respect to each reactant and the overall order? Also calculate the rate constant and wriye its units.10:00View SolutionWhat is the ratio of `t_(1//2)` to `t_(1//3)` (for the amount of substance left) for first order reaction ?
02:40View SolutionThe half life for a given reaction was doubled as the initial concentration of a reactant was doubled. What is the order of reaction.
02:29View SolutionWhy the term half life is not used for second order reaction?
01:57View SolutionThe reaction `SO_(2)Cl_(2) overset(k_(1))rarr SO_(2)+Cl_(2)` is a first order reaction with `k_(1) = 2.2 xx 10^(-5) s^(-1)` at `575 K`. What percentage of `SO_(2)Cl_(2)` will get decomposed in `90 min` when the reaction is carried out at `575 K`.
03:36View SolutionA first order reaction has a specific reaction rate of `10^(-3) s^(-1)`. How much time will it take for `10 g` of the reactant to reduce to `2.5 g`. (Given `log4 = 0.6021`).
01:53View SolutionThe esterification of acetic anhydride by ethyl alcohol can be represented by the following balanced equation:
`underset(A)((CH_(3)CO)_(2)O) + underset(B)(C_(2)H_(5)OH) rarrCH_(3)COOC_(2)H_(5) + CH_(3)COOH`
When the reaction is carried out in dilute hexane solution, the rate may be represented by `k[a][b]`. When ethyl alcohol `(B)` is the solvent, the rate may be represented by `k[A]` the values of `k` are not the same in the two cases). Explain the difference in the apparent order of the reaction.View SolutionAn optically active drug has one chiral centre and only dextro rotatory isomer is effective. Moreover, it becomes ineffective when its optical activity is reduced to `35%` of original. It was found that mutarotation of this drug was first order reaction with a rate constant of `1 xx 10^(-8) s^(-1)`. Find the expiration time of the drug in years.
03:19View SolutionA radioactive element `(t_(1//2) = 50 days)` is spread over a room. Its activity is `30` times the permisisble value for safe working. Calculate the number of days after which the room will be available for safe working.
02:39View Solution`._(84)Po^(218) (t_(1//2) = 3.05 min)` decays to `._(82)Pb^(214) (t_(1//2) = 2.68 min)` by `alpha` emisison while `Pb^(214)` is `beta`-emitter. In an experiment starting with `1 g` atom of pure `Po^(218)`, how much time would be required for the concentration of `Pb^(214)` to reach maximum?
04:56View SolutionThe complex `[Co(NH_(3))_(5)F]^(2+)` reacts with water according to the equation
`[Co(NH_(3))_(5)F]^(2+)+H_(2)O rarr[Co(NH_(3))_(5)(H_(2)O)]^(3+) + F^(ɵ)` and Rate `= k["Complex"]^(a)[H^(o+)]^(b)`
The reaction is acid catalyzed, i.e., `[H^(o+)]` does not change during the reaction.
Thus, rate `=k'["Complex"]^(3)`, where `k' = k[H^(o+)]^(b)`
Calculate `a` and `b` form the following data `(t = 25^(@)C)`
 05:28View Solution
05:28View SolutionFor the reaction

`k_(1) = 1.78 xx 10^(-3)s^(-1)` and `k_(2) = 5.8 xx 10^(-5)s^(-1)` for the initial concentration of `[Cr(H_(2)O)_(4)Cl_(2)]^(o+)` is `0.0174 mol L^(-)` at `0^(@)C`. Calculate the value of time at which the concentration of `[Cr(H_(2)O)_(5)Cl]^(2+)` is maximum.03:21View SolutionSubstance `A` isomerizes according to a first order rate law with `k = 5.0 xx 10^(-5) s^(-1)`.
(a) If the initial concentration of `A` is `1.00 M`, what is the initial rate?
(b) What is the rate after `1.00 hr` ?03:49View SolutionA certain reaction `A + B rarr` Products is first order w.r.t. each reactant with `k = 5.0 xx 10^(-3) M^(-1) s^(-1)`. Calculate the concentration of `A` remaining after `100s` if the initial concentration of `A` was `0.1 M` and that of `B` was `6.0 M` State any approximation made in obtaining your result.
04:41View SolutionThe progress of the reaction `A hArr nB`, with times is presented in the figure below.
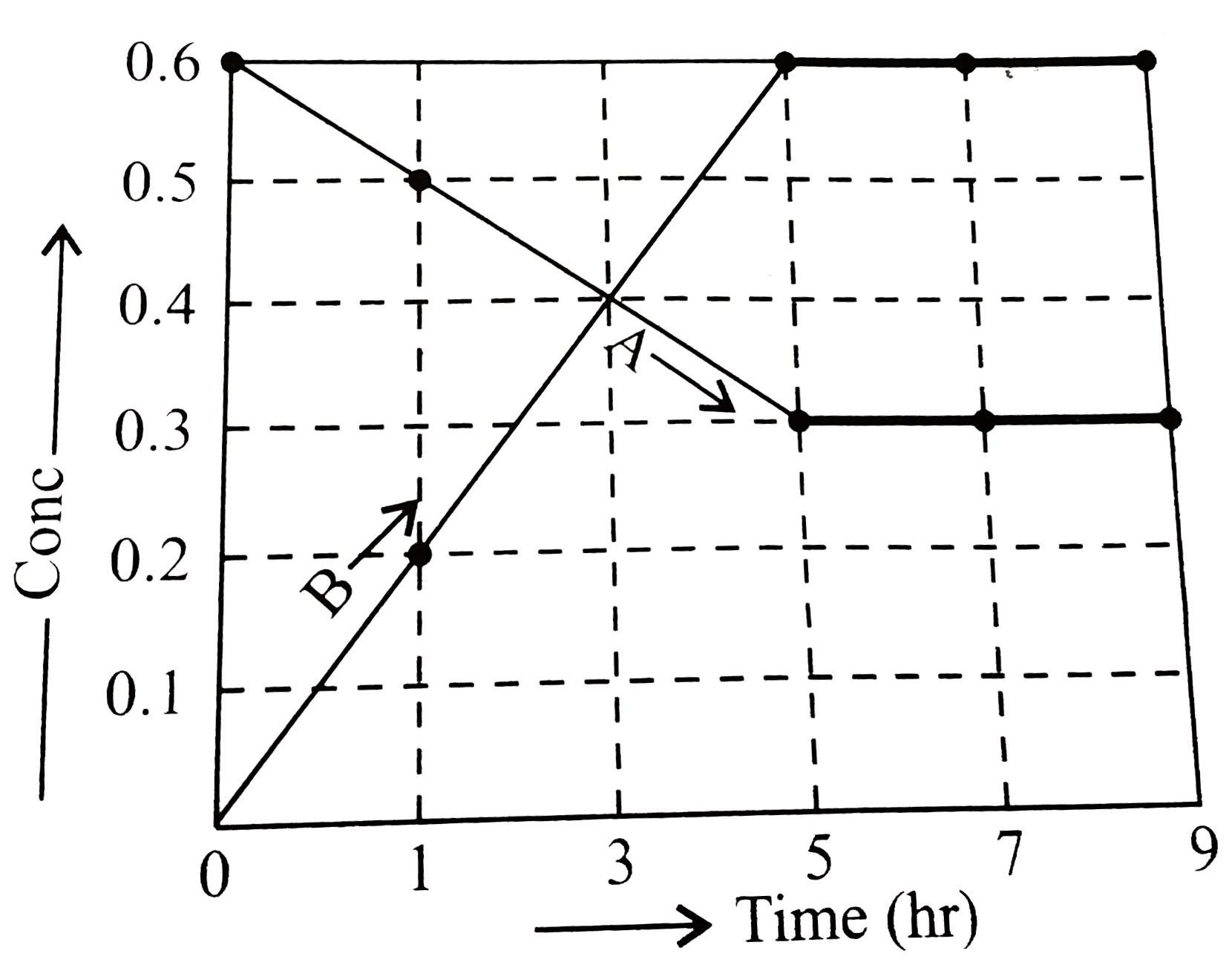
Determine:
(a) The value of `n` , (b) `K_(eq)`
( c) Initial rate of converison of `A`04:46View SolutionAt constant temperature and constant `pH` of `4`, the inverison of sucrose proceeds with a constant half life of `300 min`. At the same temperature but at `pH` of `3` the half life is constant at `30 min`. Calculate the order of reaction w.r.t. sucrose and w.r.t. `[H^(o+)]`.
06:33View SolutionIn a certain polluted atmosphere containing `O_(3)` at a steady-state concentration of `2.0 xx 10^(-8) mol L^(-1)`, the hourly Production of `O_(3)` by all sources was estimated as `7.2 xx 10^(-15) mol L^(-1)`. If only mechanism for the destruction of `O_(3)` is the second order reaction,
`2O_(3) rarr 3O_(2)`
Calculate the rate constant for the destruction reaction defined by the rate law for `-Delta[O_(3)]//Delta t`.03:53View SolutionWrite a rate expresison for each speices. Assuming `[B]` is constant, write a rate expresison for `[A]` and `[C]` so that they do not contain `[B]` term. Under what conditions will the reaction be pseudo first order to second conditions will the reaction be pseudo first order to second order ?
Mechanism of reaction is
`A underset(k_(2))overset(k_(1))hArr B`
`{:(B+Aoverset(k_(3))rarrC:}/{:(2ArarrC)/`10:12View SolutionConisder the following proposed mechanism
`A underset(k_(1))overset(k_(2))hArr B` , `B+C overset(k_(3))rarrD`
For the overall reaction `A+CrarrD`, assuming `B` to be an intermediate described by the steady state approximation, write the rate expresison for `[A]`.03:58View SolutionConisder the following proposed mehanism
`A_(2) hArr 2A (k_(1))`
`A+B hArr C(k_(2))`
`A_(2) + C rarr D + A (k)`
For the overall chemical equation `A_(2)+BrarrD`, assuming that the equlibria are rapidly established in the first two steps, write the rated expresison for `[D]`.03:31View SolutionConisder the following mechanism:
`A_(2) hArr 2A (k)`
`A+B_(2)overset(k_(1))rarrC+B`, `B+A_(2)overset(A_(2))rarrC+A`
For the overall chemical equation `A_(2)+B_(2)rarr2C`.
Assumming that the equilibrium is rapidly established and the steady approximation is valid for `[B]`, write the rate expresison for `[C]`.05:21View SolutionThe rate equation for the overall equation is:
`H_(3)AsO_(4) (aq)+2H^(o+) + 3I^(Θ)(aq) underset(k_(r ))overset(k_(f))hArr H_(3)AsO_(3)(aq)+I_(3)^(Θ)(eq)+H_(2)O(l)`
`(d[I_(3)^(ɵ)])/(dt)=k_(f)[H_(3)AsO_(4)][I^(ɵ)][H^(o+)]-k_(f)([H_(3)AsO_(3)][I^(ɵ)3])/{[I^(ɵ)]^(2)[H^(o+)])`
where `k_(f)= 4.7xx10^(-4)L^(2)mol^(-2)mi n^(-1)` and
`k_(r )= 3xx10^(-3)mol^(2)L^(-2)min^(-1)`
Determine the euilibrium constant for this reaction form the rate constants.04:01View Solution`H_(2)(g) + Ar(g) underset(k_(r ))overset(k_(f))hArr 2H(g)+Ar(g)`
`k_(f)= 2.2xx10^(4)Lmol^(-1)s^(-1)` and `k_(c )= 1.02xx10^(-4)` at `3000 K`. What is the value of `k_(r )`?01:32View SolutionConisder parallel reaction:
`Aoverset(k_(1))rarrB, 2Aoverset(k_(2))rarrC+D`
What would be the rate expresison for `[A]` ?01:27View SolutionConisder a mechanism in which a single reactant profuces several Products by the following parallel first order reactions :
`A overset(k_(1))rarrB, A overset(k_(2))rarrC A overset(k_(3))rarrD`
Write the rate expresison for `[A]`.02:09View SolutionA proposed mechanism for a reaction `ArarrB` is
`A underset(k_(2))overset(k_(1))hArr C " " C underset(k_(4))overset(k_(3))hArr B`
Determine the expresison for the equilibrium constant for the overall reaction in terms of the rate constants.03:20View SolutionBicyclohexane was found to undergo two parallel first order rearrangements. At `730 K`, the first order rate constant for the formation of cyclohexene was measured as `1.26xx10^(-4)s^(-1)` and for the formation of methyl cyclopentene the rate constant was `3.8 xx 10^(-5) s^(-1)`. What is the percentage distribution of the rearrangement Products ?
02:39View SolutionTrans `1,2`-dideuterocyclopropane `(A)` undergoes a first order decompoistion. The observed rate constant at a certain temperature, measured in terms of disapperance of `A` was `1.52xx10^(-4)s^(-1)`. The analyiss of Products shwoed that the reaction followed two parallel paths, one leading to dideuteropropane `(B)` and the other to cis-`1,2`-dideuterocyclopropane `(c )`. `(B)` was found to constitute `11.2%` of the reaction Product, independently of the extent of reaction. What is the order of reaction for each path and what is the value of the rate constant for the formation of each of the Products ?
04:07View SolutionThe decompoistion of `Cl_(2)O_(7)` at `400 K` in gas phase to `Cl_(2)` and `O_(2)` is a first order reaction.
a. After `55 s` at `400 K`, the pressure of `Cl_(2)O_(7)` falls form `0.062` to `0.044 atm`. Calculate `k`.
b. Calculate the pressure of `Cl_(2)O_(7)` after `100 s` of decompoistion.04:26View SolutionEthylene is profuced by
`C_(4)H_(8)("cyclobutane")overset(Delta)rarr2C_(2)H_(4)`
The rate constant is `2.48 xx 10^(-4)s^(-1)`. In what time will the molar ratio of the ethylene to cyclobutane in reaction mixture attain the value (a) `1` (b) `100`?05:14View Solutionform the following data for the decompoistion of `N_(2)O_(5)` in carbon tertrachloride solution at `321 K`, show that the reaction is of the first order and calculate the rate constant.
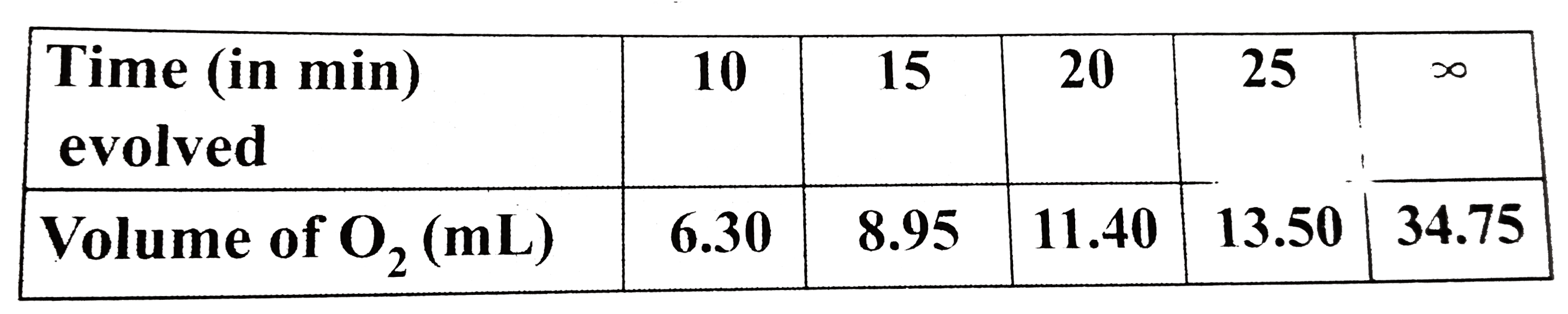 02:49View Solution
02:49View Solution`1.0 mL` of ethyl acetate was added to `25 mL` of `N//2 HCl, 2 mL` of the mixture were withdraw form time to time during the progress of the hydrolyiss of the ester and titrated against standard `NaOH` solution. The amount of `NaOH` required for titration at various intervals is given below:

The value at `oo` time was obtained by completing the hydrolyiss on boiling. Show that it is a reaction of the first order and find the average value of the velocity constant.View SolutionThe inverison of cane sugar was studied is `HCl` at `298 K`. The following polarimetric readings were obtained at different intervals of time:
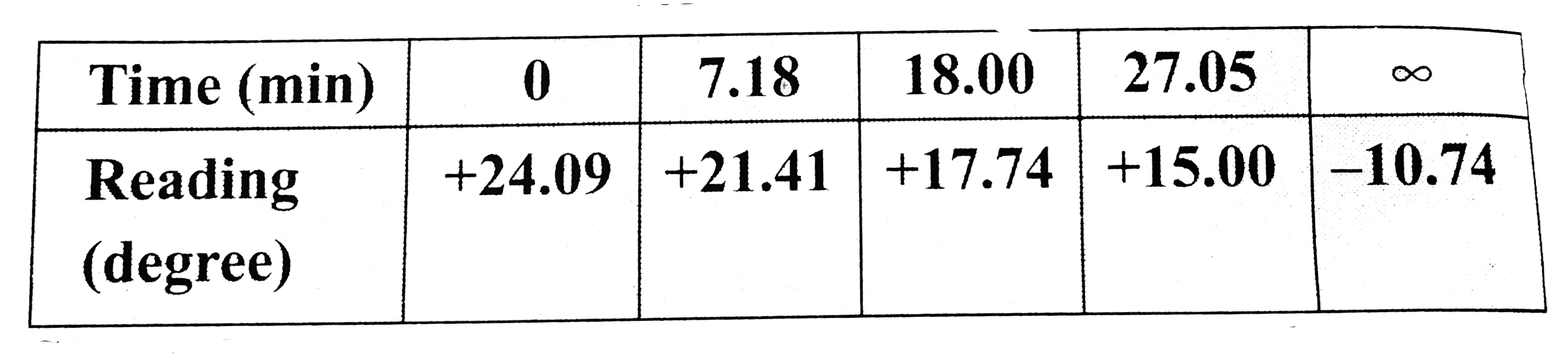
Show that the inverison of cane sugar is a unimolecular reaction.05:01View SolutionAn exothermic reaction `XrarrY` has an activation energy of `90kJ mol^(-1)` of `X` and the heat of reaction is `250 kJ`. Find the activation energy of the reaction `YrarrX`.
02:23View SolutionRefer picture given below.
(a) Calculate `DeltaH` for the reaction and the energy of activation for the forward reaction as well as backward reaction.
(b) The dotted curve is in the presence of a catalyst. What is the energy of activation for the two reactions in the presence of catalyst?
( c) Will the catalyst change the extent of reaction?
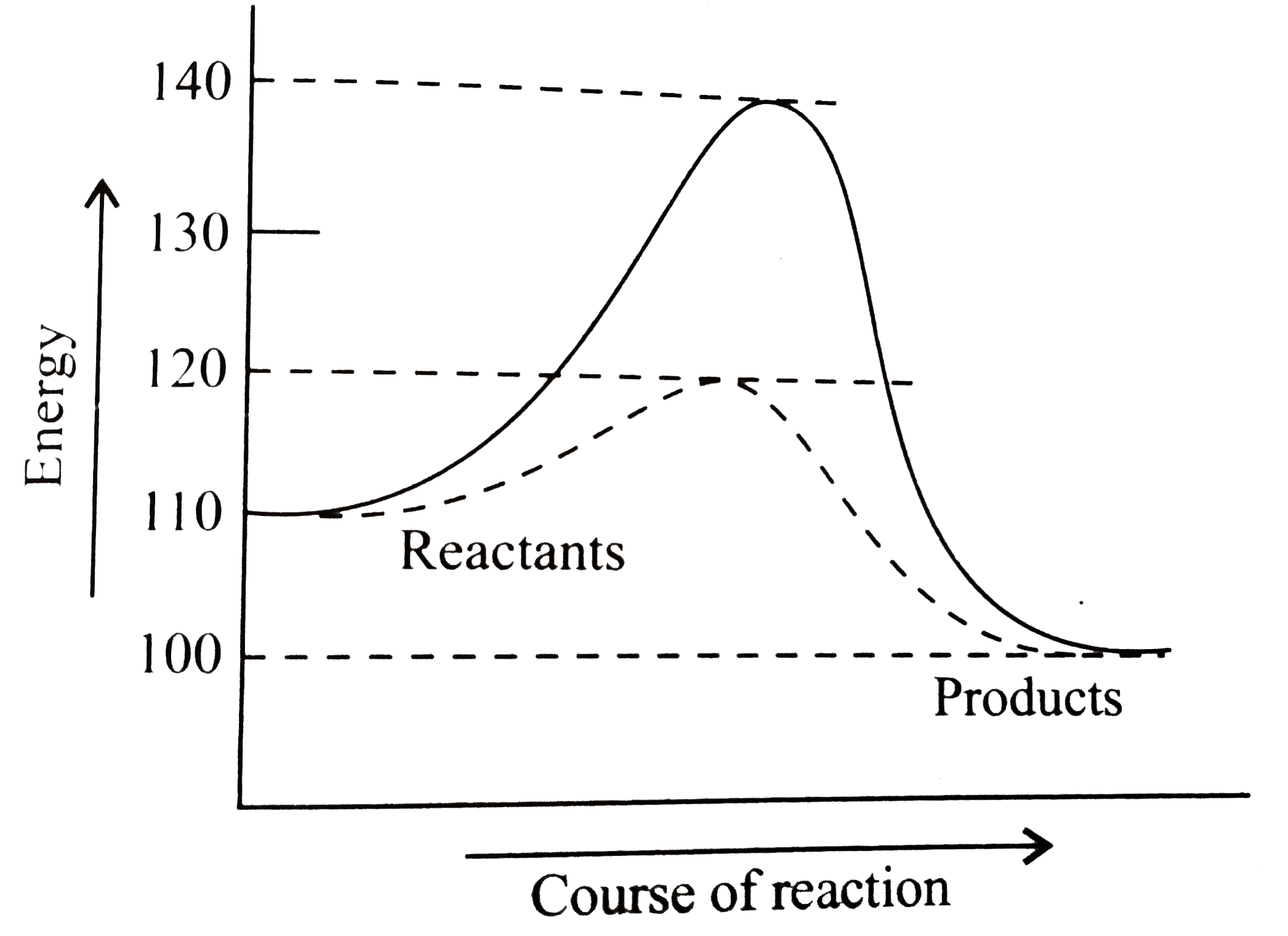 04:24View Solution
04:24View SolutionCalculate the activation energy of a reaction whose reaction rate at `300 K` double for `10 K` rise in temperature.
02:41View SolutionThe activation energy of a reaction is `94.14 kJ mol^(-1)` and the value of rate constant at `313 K` is `18 xx 10^(-5) s^(-1)`. Calculate the frequency factor or pre-exponential factor, `A`.
03:47View SolutionThe rate constant of a reaction is `1.5 xx 10^(7)s^(-1)` at `50^(@)C` and `4.5 xx 10^(7) s^(-1)` at `100^(@)C`. Evaluate the Arrhenius parameters `A` and `E_(a)`.
04:11View SolutionFor two reactions (i) `P rarr` Product and (ii) `Q rarr` Product, the order of reaction (i) is `1` while that of reaction (ii) is `2`. At `347 K`, the energy of activation of reaction (i) is `55 kJ mol^(-1)` but whenever this reaction is carried out in the presence of catalyst at the same temperature, the energy of activation is `53 kJ mol^(-1)`. Moreover, for reaction (ii), when the temperature is increased form `298 K` to `308 K`, the rate of reaction increases as many times as for reaction (i) in the presnece of catalyst. Calculate the rate constant of reaction (ii) at `318 K`, if the pre-exponential factor for reaction (ii) is `3.56 xx 10^(9) mol^(-1) L s^(-1)`.
Note: Arrhenius equation does not depend on the order of reaction.08:35View SolutionFor two firstorder reactions having same concentration of `A` and `B` at `t = 0`, use the given data to calculate the tempretature at which both occur with same rate.
Reaction I: `ArarrZ`, `k_(1) = 10^(16)e^((-(3000)/(T)))`
Reaction II: `BrarrY`, `k_(2) = 10^(15) e^((-(2000)/(T)))`03:04View SolutionThe Arrehenius equation for the rate constant of decompoistion of methyl nitrite and ethyl nitrite are
`k_(1) (s^(-1)) =10^(13) exp ((-152300 J mol^(-1))/(RT))`
and `k_(2)(s^(-1)) = 10^(14)exp((-157700 J mol^(-1))/(RT))` respectively. Find the temperature at which the rate constant are equal.02:46View SolutionThe activation energy of the reaction: `A + B rarr` Products is `105.73 kJ mol^(-1)`. At `40^(@)C`, the Products are found at the rate of `0.133 mol L^(-1) min^(-1)`. What will be the rate of formation of Products at `80^(@)C`?
04:37View SolutionFor a reverisble reaction `A hArr B`, if pre-exponential factor is same for both forward and backward reactions, show that `k_(eq) = e^(-DeltaH//RT)`, where `Delta H` is the heat of reaction.
02:27View SolutionTwo reaction : `X rarr` Products and `Y rarr` Products have rate constants `k_(1)` and `k_(2)` at temperature `T` and activation energies `E_(1)` and `E_(2)`, respectively. If `k_(1) gt k_(2)` and `E_(1) lt E_(2)` (assuming that the Arrhenius factor is same for both the Products), then
(I) On increaisng the temperature, increase in `k_(2)` will be greater than increaisng in `k_(1)`.
(II) On increaisng the temperature, increase in `k_(1)` will be greater than increase in `k_(2)`.
(III) At higher temperature, `k_(1)` will be closer to `k_(2)`.
(IV) At lower temperature, `k_(1) lt k_(2)`02:09View SolutionThe decompoistion of compound `A` in solution is a first order process with an activation energy of `52.3 kJ mol^(-1)`. A `10%` solution of `A` is `10%` decomposed in `10 min` at `10^(@)C`. How much decompoistion would be observed with a `20%` solution after `20 min` at `20^(@)C`.
03:08View Solution
Solved Example questions and complete solutions for chapter CHEMICAL KINETICS of CENGAGE CHEMISTRY (HINGLISH) of Class 12
All Exercises from CENGAGE CHEMISTRY Class 12 CHEMISTRY CHEMICAL KINETICS
- Archives Fill In The Blanks
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives Subjective
- Archives True/False
- Ex 4.1 (Objective)
- Ex 4.2 (Objective)
- Ex 4.3 (Objective)
- Ex 4.3 More Than One Correct
- Ex4.4 Objective
- Exercises Assertion-Reasoning
- Exercises Fill In The Blanks
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises True/False
- Illustration
- Solved Example
