Complete Solutions to Illustration of chapter SOLID STATE of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | SOLID STATE |
| CENGAGE CHEMISTRY | Illustration |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
A sample of a crystalline solid scatters a beam of X-rays of wavelength `70.93` pm at an angle `2 theta` of `14.66^(@)`. If this is a second-order reflection `(n = 2),` calculate the distance between the parallel planers of atoms from which the scattered beam appears to have been reflected.
View SolutionCalculate `lambda` of X-rays which give a diffraction angle `2 theta = 16.8^(@)` for crystal, if the interplanar distance in the crystal is `0.2 nm` and that only for the first-order diffraction is observed. Given `sin 8.40^(@) = 0.146`.
View SolutionA compound formed by elements `X` and `Y` has a cubic structure in which `X` atoms are at the corner of the cube and `Y` atoms are at the face centres. One atoms `X` is misssing from the corner.
a. Calculate (i). `Z_(eff')` (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) `Z_(eff')` (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionA compound formed by elements `X` and `Y` has a cubic structure in which `X` atoms are at the corners of the cube of and two atoms `(Y)` are at each body diagonal of the cube.
a. Calculate: (i) `Z_(eff')` (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all atoms form one body diagonal of the cube except corners are removed, calculate: (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionA compound formed by elements `X` and `Y` has a cubic structure in which `X` atoms are at the corner of the cube and `Y` atoms are at the face centres. One atoms `X` is misssing from the corner.
a. Calculate (i). `Z_(eff')` (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) `Z_(eff')` (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionA compound formed by elements `X` and `Y` has a cubic structure in which `X` atoms are at the corner of the cube and also at the face centers. `Y` atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionA compound formed by elements `X` and `Y` has a cubic structure in which `X` atoms are at the corner of the cube and also at alternate face entres. `Y` atoms are present at the body centre and also at the alternate edge centre of the cube.
a. Calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the plane passing through the middle of the cube of the cube which contains atoms both on the edge entre as well as on the face centre, calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, (iii) formula of the compound.
c. If all the atoms are removed from the plane passing through the middle of the cube which contains atoms only on the edge centre but not on face centre, calculate (i) `Z_(eff')` (ii) total number of atoms in t he cube, and (iii) fomula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of the cube which neither contains atoms on the edge centre nor on the face centre, calculate (i) `Z_(eff')` (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from on e of the axes passing through the middle of the cube containing face centre atoms, calculate (i) `Z_(eff')` (ii) total number of atoms in a cube, and (iii) formula of the compound.
f. If all the atoms are remove from one of the axes passing through the middle of the cube nor containing face centre atoms, calculate (i) `Z_(eff')` (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionDraw a two-dimesnsional haxagonal lattice. Try to visualize the possibility of pentagonal two-dimensional lattice.
View SolutionConsider the parallelotrams shown in the figure below representing two-dimensional cells.
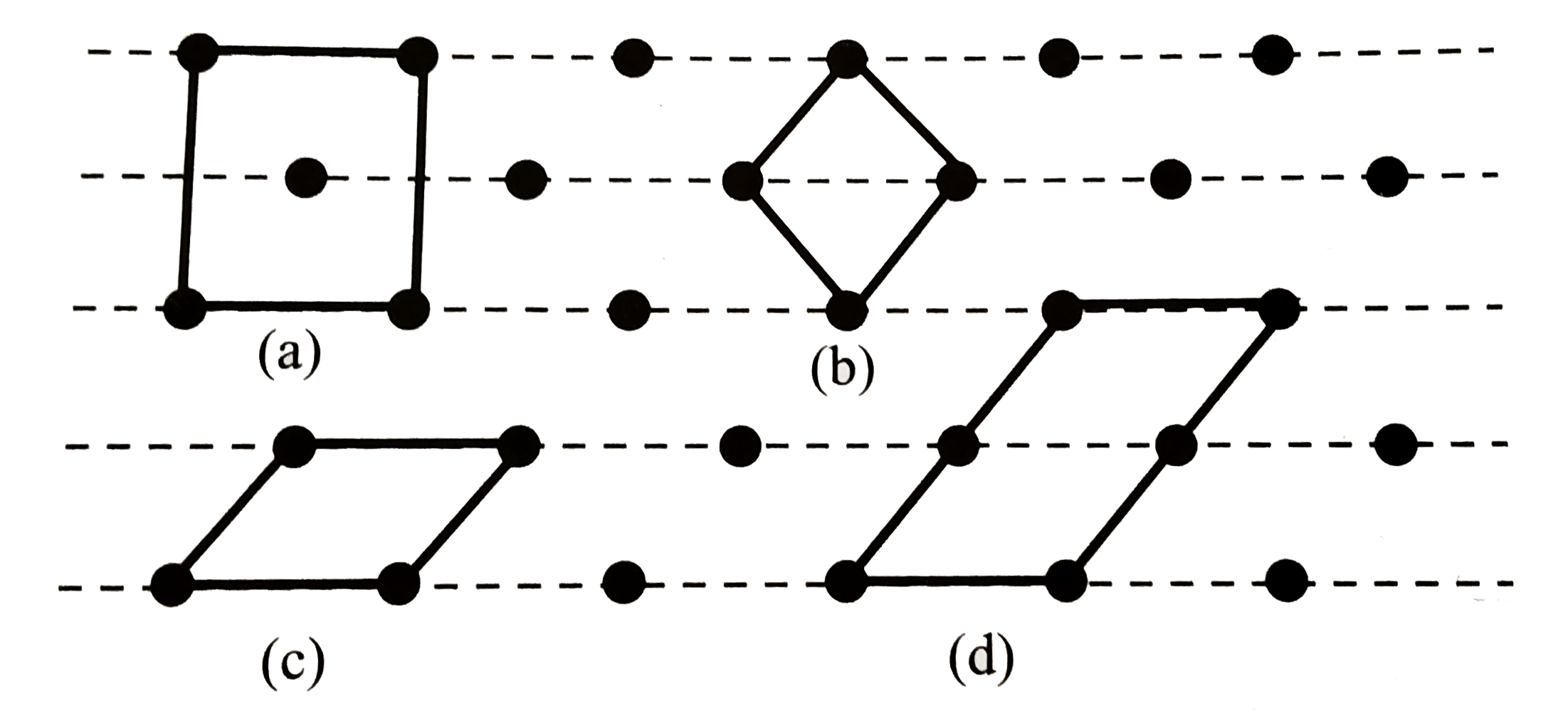
a. Which of these are primitive and which are multiple unit cells? Are any of these orthogonal?
c. What is the relation between the radius of circle and the length of parallelogram for the unit cell shown in the figure below (space filling diagram)?
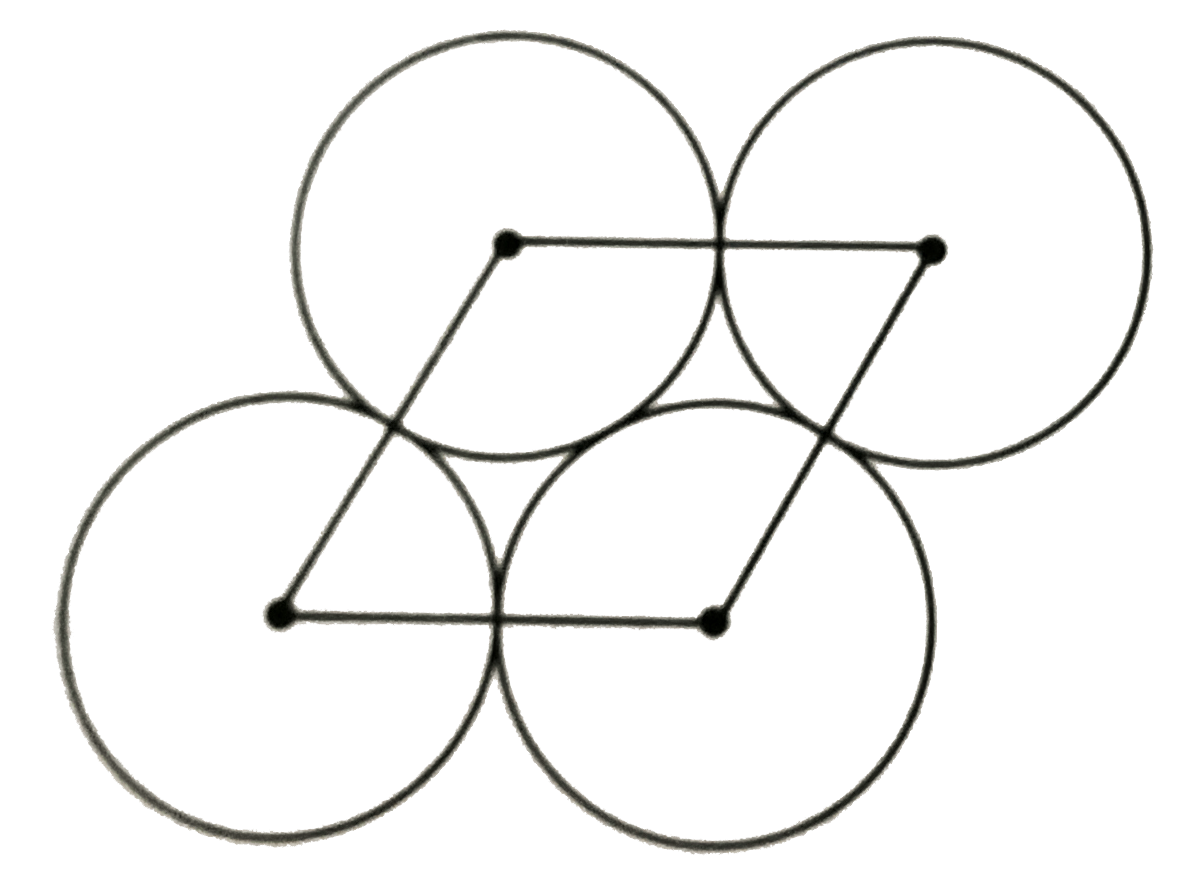
d. How many nearest neighbour circles does a given circle have in the second figure abov?
e. What is the radius of the triangular hole shown in the second figure above?
f. What is the packing fraction of the unit cell in the second figure above?
View SolutionWhy uncharged atoms or molecules never crystallize in simple cubic lattice ?
View SolutionWhy an end-centred unit cell cannot he cubic? What is the highest possible symmetry for this type of unit cell?
View SolutionExplain why a hexagonal close-packed structure and a cubic close packed structure for a given element would be expected to have the same density ?
View SolutionSelect the close-packing arrangements in the following:
a. … `ABABABA` …, b. … `ABCABCABCA` …
c. … `ABABCBCABC` … , d. … `AC CBCABCABC` …
View SolutionA compound is formed by two elements `X` and `Y`. Atoms of the element `Y` (as anion) make ccp and those of element `X` (as cation) occupy all the octahedral voids. What is the formula of the compound?
View SolutionAtoms of elements `B` from hep lattice and those of element `A` occupy two-thirds of tetrahedral voids. What is the formula of the compound formed by elements `A` and `B`?
View SolutionAn element has a bcc structure with a cell edge of `288` pm. The density of the element is `7.2 g cm^(-3)`. How many atoms are present in `208 g` of the element?
View SolutionX-ray diffraction studies show that copper crystallizes in an fcc unit cell with cell edge of `3.608 xx 10^(-8)` cm. In a separate experiment, copper is determined to have a density of `8.92 g//cm^3` calculate the atomic mass of copper.
View SolutionSilver forms ccp lattice and X-ray studies of its crystals show that the edge length of its unit cell is 408.6 pm. Calculate the density of silver (Atomic mass = 107.9u).
View SolutionMetallic gold crystallizes in the fcc lattice.
The length of the cubic unit cell is `a = 4.242 A`.
a. What is the closest distance between gold atoms?
b. How many "nearest neighbours" does each gold atom have at the distance calculated in `(a)`?
(c) What is the density of gold? (Aw of Au `= 197.0 g mol^(-1)`)
d. Prove that the packing factor for gold is `0.74`.
View SolutionIf the radius of an atom of an elements is `75` pm and the lattice type is body-centred cubic, what is the edge length of the unit cell?
View SolutionThe radius of an atom of an element is `500` pm. If it crystallizes as a face-centred cubic lattice, what is the length of the side of the unit cell?
View SolutionSodium has a `bc c` structure with nearest neighbour distance of `365.9` pm. Calculate its density. (Atomic mass of sodium `= 23`)
View SolutionA face-centred cubic element (atomic mass `60`) has a cell edge of `400` pm. What is its density?
View SolutionXenon crystallizes in the face-centred cubic lattice and the edge of the unit cell is `620` pm. What is the nearest neighbour distance and what is the redius of xenon atom?
View SolutionIn a compound, oxide ions are arranged in `ccp`. One-sixth of the tetrahedral voids are occupied by cations. `(A)` and one-third of `OV_(s)` are occupieed by cations `(B)`. (a) What is the formula of the compound of the compound? (b) What are the charges on `A` and `B` ?
View SolutionA compund is made of two elements `P` and `Q` are in `ccp` arrangement while atoms `P` occupy all the tetrahedral voids. What is the formula of the compound?
View SolutionTwo ions `A^(o+)` and `B^(Θ)` have radii `88` and `200` pm, respectively. In the close-packed crystal of compound `AB`, predict coodination number of `A^(o+)`.
View SolutionIf the close-packed cations in an `AB`-type solid gave a radius of `75` pm. What would be the maximum and minimum sizes of the anions filling the voids?
View SolutionIf the radii of `Mg^(2+), Cs^(o+), O^(2-), S^(2-)`, and `CI^(Θ)` ions are `0.65, 1.69, 1.40, 1.84`, and `1.81 Å`, respectively, calculate the coordination number of the cation in the crystals of `MgS, MgO`, and `C_(s)CI`.
View SolutionWhenever two-demiensional square packing same layers are kept in the way so that the centres are aligned in all three dimensation, coordination numberof each sphere is
View SolutionIn an `fcc` crystal, which of the following shaded planes contain the given `(rarr)` type of type of arrangement of atoms?

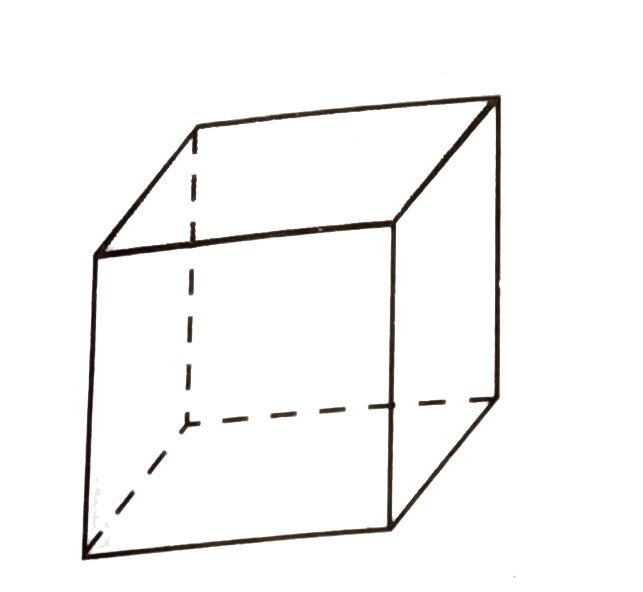
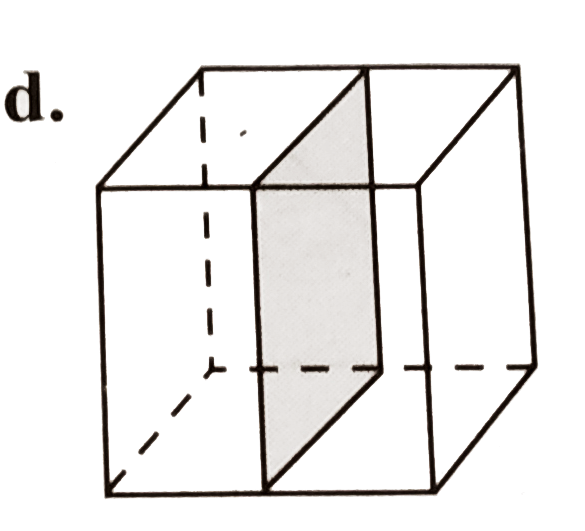
View SolutionIn hexagonal close packing of spherer in three dimensions.
View SolutionThe coordination number of an `fcc` structure for a metal is `12`, since
View SolutionWhich of the following statements is correct for a two-dimensional haxagonal close-packed layer?
View SolutionA compound made of particles `A`, `B`, and `C` forms `ccp` lattice. Ions `A` are at lattice points, `B` occupy `TV_(s) C` occupy `OV_(s)`. If all the ions along one of the edge axis are removed, then formula of the compound is
View SolutionA compound made of particles `A`, `B`, and `C` forms `ccp` lattice. In the lattice, ions `A` occupy the lattice points and ions `B` and `C` occuphy the alternate `TV_(s)`. If all the ions along one of the body diagonals are removed, then formula of the compound is
View SolutionA compound made of particles `A` and `B`. A forms `fc c` packing and `B` occupies all the `OV_(s)`. If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is

View SolutionIn a solid having rock salt structure, if all tge atoms touching one body diagonal plane are removed (except at body centre), then the formula of the left unit cell is
View SolutionCalculate the value of Avogadro's number from the following data:
Density of `NaCl = 2.165 g cm^(-3)`
Distance between `Na^(o+)` and `Cl^(Θ)` in `NaCl = 281` pm
View Solution`CsCl` has `bc c` arrangement and its unit cell edge length is `400` pm. Calculate the interionic distance in `CsCl`.
View SolutionA solid `AB` has `CsCl`-type structure. The edge length of the unit cell is `404` pm. Calculate the distance of closest approach between `A^(o+)` and `B^(Θ)` ions.
View Solution`CsCl` has cubic structure. Its density is `3.99 g cm^(-3)`. What is the distance between `Cs^(o+)` and `Cl^(Θ)` ions?
(Atomic mass of `Cs = 133`)
View SolutionThe unit cube length for `LiCl` (`NaCl` structure) is `5.14 Å`. Assuming anion-anion contact, calculate the ionic radius for chloride ion.
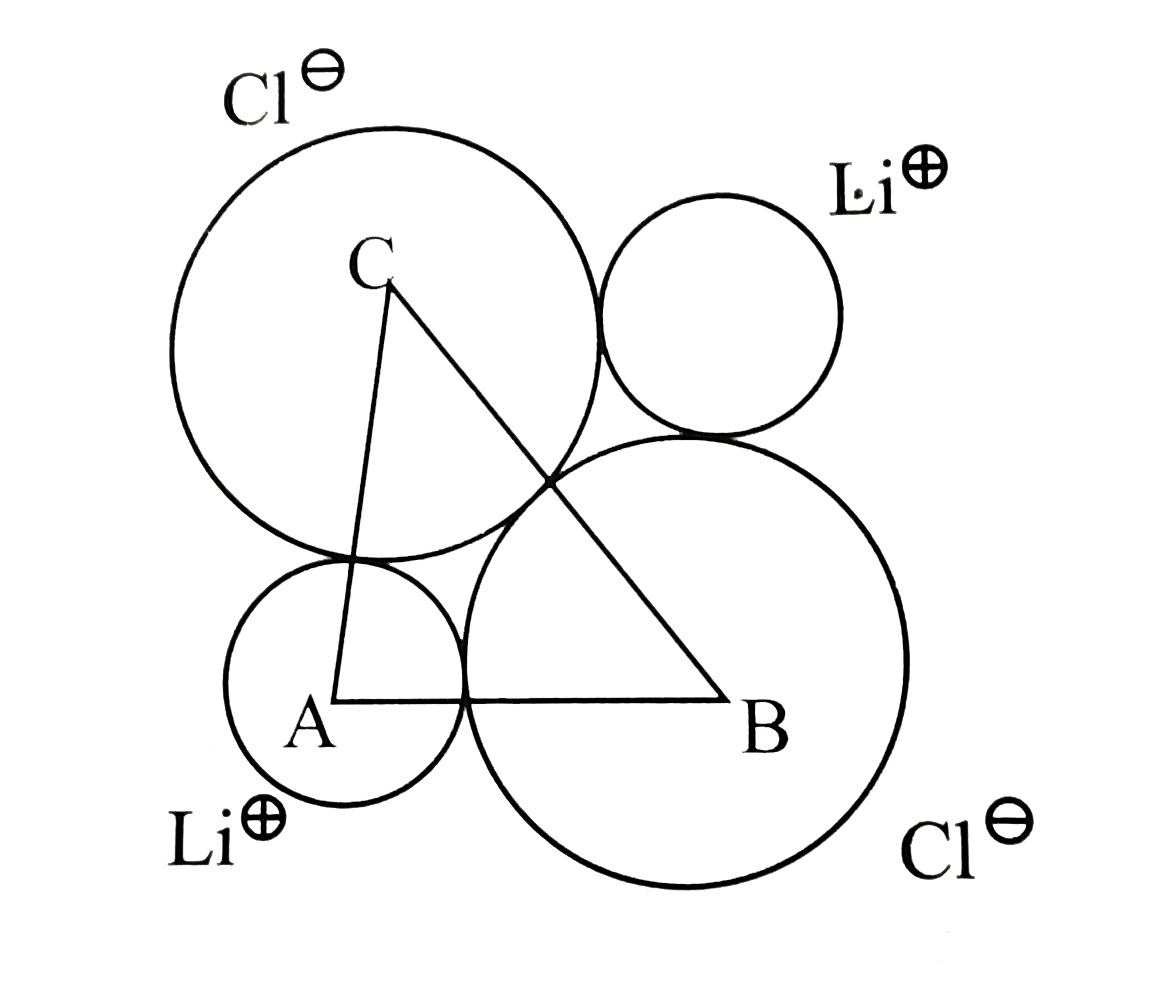
View SolutionCasium may be considered to form interpentrating simple primitice cubic crystal. The edge length of unit cell is `412` pm. Determine
a. The density of `CsCl`.
b. The inoic radius of `Cs^(o+)` if the ionic radius of `Cl^(Θ)` is `181` pm. Given: `Aw (Cs) = 133 g mol^(-1)`
View Solution`KCI` crystallizes in the same type of lacttice as does `NaCl`. Given that
`(r_(Na^(o+)))/(r_(Cl^(Θ))) = 0.5` and `(r_(Na^(o+)))/(r_(K^(o+))) = 0.7`
Calculate (a) the ratio of side of the unit cell for `KCl` to that for `NaCl`, and (b) the ratio of density of `NaCl` to that `KCl`.
View Solution`LiI` occurs as cubical closed packing. If the edge lenth of unit cell is `624` pm, determine the ionic radii of `Li^(o+)` and `I^(Θ)` inos.
View SolutionThe composition of a sample of Wustite is `Fe_(0.93)O_(1.00)`. What percentage of the iron is present in the form of `Fe (III)`?
View Solution`CsBr` crystallizes in a body-centred cubic unit lattice with an edge length of `4.287 Å`. Calculate the angles at which the second-order reflection maxima may be expected for `(2, 0, 0)`, `(1, 1, 0)`, planes when `X`-rays of `gamma = 0.50 Å` are used.
View SolutionCalculate the miller indices of crystal. Planes which cut through the crystal axes at
View SolutionHow do the spacings of the three planes `100`, `110`, and `111` of cube lattice vary?
View SolutionPotassium chloride crystallize with a body-centred cubic lattice. Calculate the distance between the `200, 110,` and `222` Planes. The length of the side of the unit cell is `5.34 Å`.
View SolutionDiamond has face-centred cubic lattice. There are two atoms at `(0, 0, 0)` and `((a)/(4), (a)/(4), (a)/(4))` coordinates. The ratio of the carbon-carbon bond distance to the edge of the unit cell is
View SolutionWhich of the following statements is(are) correct for the diamond structure?
View SolutionWhich of the following compounds are not isomorphous?
a. Copper sulphate and zine sulphate
b. Zinc sulphate and manganeous sulphate
c. Calcium carbonte and ferrous sulphate
d. Zine sulphate and ferrous sulphate
View SolutionPotassium selenate is isomorphous with potassium sulphate and contains `50.0%` of `Se`. The atomic weight of `Se` is
a. `142`, b. `71`, c. `47.33`, d. `284`
View SolutionThe `Ew` of an element is `13`. It forms an acidic oxide which `KOH` forms a salt isomorphous with `K_(2)SO_(4)`. The `Aw` of element is
a. `13`, b. `26`, c. `52`, d. `78`
View SolutionIf NaCl is doped with `10^(-3)mol%` of `SrCl_(2)`, what is the concentration of cation vacancies ?
View SolutionIf `NaCl` is doped with `10^(-3) mol% GaCl_(3)`, what is the concentration of the cation vacancies?
View SolutionIf all the atoms touching one face plane are removed in solid `A^(o+)B^(Θ)` having rock salt type structure, then the formula of the compound left and the defect brought by this removal, respectively, is
a. `AB`, Frenkel defect
b. `A_(2)B`, Frenkel defect
c. `AB`, Schottky defect
d. `A_(2)B`, Schottky defect
View SolutionThe addition of `CaCl_(2)` crystal to `KCl` crystal
a. Lowers the density of the `KCl` crystal
b. Raises the density of the `KCl` crystal
c. Does not affect the density of the `KCl` crystal
d. Increases the Frenkel defects of the `KCl` crystal
View SolutionWhat fraction of the surface of a crystal of `Cd` at `T = 298 K` consists of vacancies? Assume that the energy needed to form a vacancy `= 0.5 Delta_("sub")H^(Θ)`. For `Cd(s), Delta_("sub")H^(Θ) = 112.0 kJ mol^(-1)`.
View SolutionCalcium crystallizesin `fcc` unit cell with `0.556 nm`. Calculate the density if
a. It contains `0.2%` Frenkel defects
b. It contains `0.1%` Schottky defects
View Solution
Illustration questions and complete solutions for chapter SOLID STATE of CENGAGE CHEMISTRY (ENGLISH) of Class 12
All Exercises from CENGAGE CHEMISTRY Class 12 CHEMISTRY SOLID STATE
- Ex 1.1 (Objective)
- Ex 1.1 (Subjective)
- Ex 1.2 (Objective)
- Ex 1.2 (Subjective)
- Exercises (Archives ) Assertion-Reasoning
- Exercises (Archives ) Interger
- Exercises (Archives ) Linked Comprehension
- Exercises (Archives ) Multiple Correct
- Exercises (Archives ) Single Correct
- Exercises (Archives ) Subjective
- Exercises (Assertion-Reasoning)
- Exercises (Fill In The Blanks)
- Exercises (Interger)
- Exercises (Linked Comprehension)
- Exercises (Multiple Correct)
- Exercises (Single Correct)
- Exercises (True/False)
- Illustration
- Solved Examples