Complete Solutions to Exercise 5.1 of chapter ELECTRIC CURRENT AND CIRCUIT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CURRENT AND CIRCUIT |
| CENGAGE PHYSICS | Exercise 5.1 |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
How many electrons per second pass through a section of wire carrying a current of `0.7A`?
View SolutionA current of `7.5 A` is maintained in wire of `45 s`. In this time
(a) how much charge and
(b) how many electrons flow through the wire?
View SolutionIf 0.6 mol of electorns flows throutgh a wire in 45 min, what are (a) the total charges that passes through the wire and (b) the magnitude of the current?
View SolutionA typical copper wire might have `2xx10^(21)` free electrons in 1 cm of its length. Suppose that the dirft speed of the electrons along the wire is `0.05 cm s^(-1).` How many electrons would pass through a given cross section of the wire each second. How large would a current be flowing in the wire?
View SolutionA coil of wire has a resistance of `25.00Omega at 20^@ C` and a resistance of `25.17Omega at 150^@C`. What is its temperauture cofficient of resistance?
View SolutionA metal wire of diameter 2mm and of length 300m has a resistance of `1.6424 Omega at 20^@C` and `2.415Omega at150^@C`. Find the values of `alpah, R_0` and `rho_0` where the zero subscript refers to `0^@C`, and `rho_0` Identify the metal.
View SolutionIt is desired to make a `20Omega` coil of wire, which has a zero thermal coefficient of resistance. To do this, a carbon resitor fo resistane `R_1` is placed in series with an iron resistor of resistance `R_2` the proportions of iron and carbon are so chosen that `R_1 +R_2 = 20Omega` for all temperatures near `20^@C.` How long are `R_1 and R_2`? `alpha_(carbon) =- 0.5xx10^(-3).^@C^(-1), alpha_(iron) = 5xx10^(-3) .^@C(-1)`
View SolutionA resistance thermometer measures temperature with the increase in resistance of a wire of high temperature. If the wire is platinum and has resistance of `10Omega` at `20^@C` and a resistance of `35Omega` in a hot furnace, what is the temperature of the hot furnace? `(alpha_("platinum") = 0.0036^@C^(-1))`
View SolutionThough the drift velocity of electorn responsible for current in a conductorn under ordinary circumstances is very small, light in a room turn on immediately after the swithc is closed, Explain why and how?
View Solutiona. A steady current flows in a metallic conductor of non - uniform cross section. State which of the quantities i.e., current density, electric field, and drift velocity remain constant?
b. A steady current passes through a cylindrical conductor. Is there an electorn field inside the conductor?
View SolutionA potential difference V is applied to copper wire of diameter d and length L, what will be the effect on, the electron drift speed by doubling (a) voltage V, (b) length L, and (c ) diameter d?
View SolutionA wire has a resistance R. What will be its resistace if (a) it is double on itself and (b) it is stretched so that (i) its length is double and (ii) its radius is halved.
View SolutionThe current in a wire varies with time according to the equation `I = 4 +2 t.` where I is in ampere and t is in second. Calculate the quantity of charge that passes through a cross section of the wire during the tiem t = 2s, to t=6s.
View SolutionThe following table gives the length of three copper rods, their diameters, and the potential differences between their ends. Rank the rods according to (a) the magnitude of the electric field within them, (b) the current density within them, and (c ) the drift speed of electrons through them, greates first.

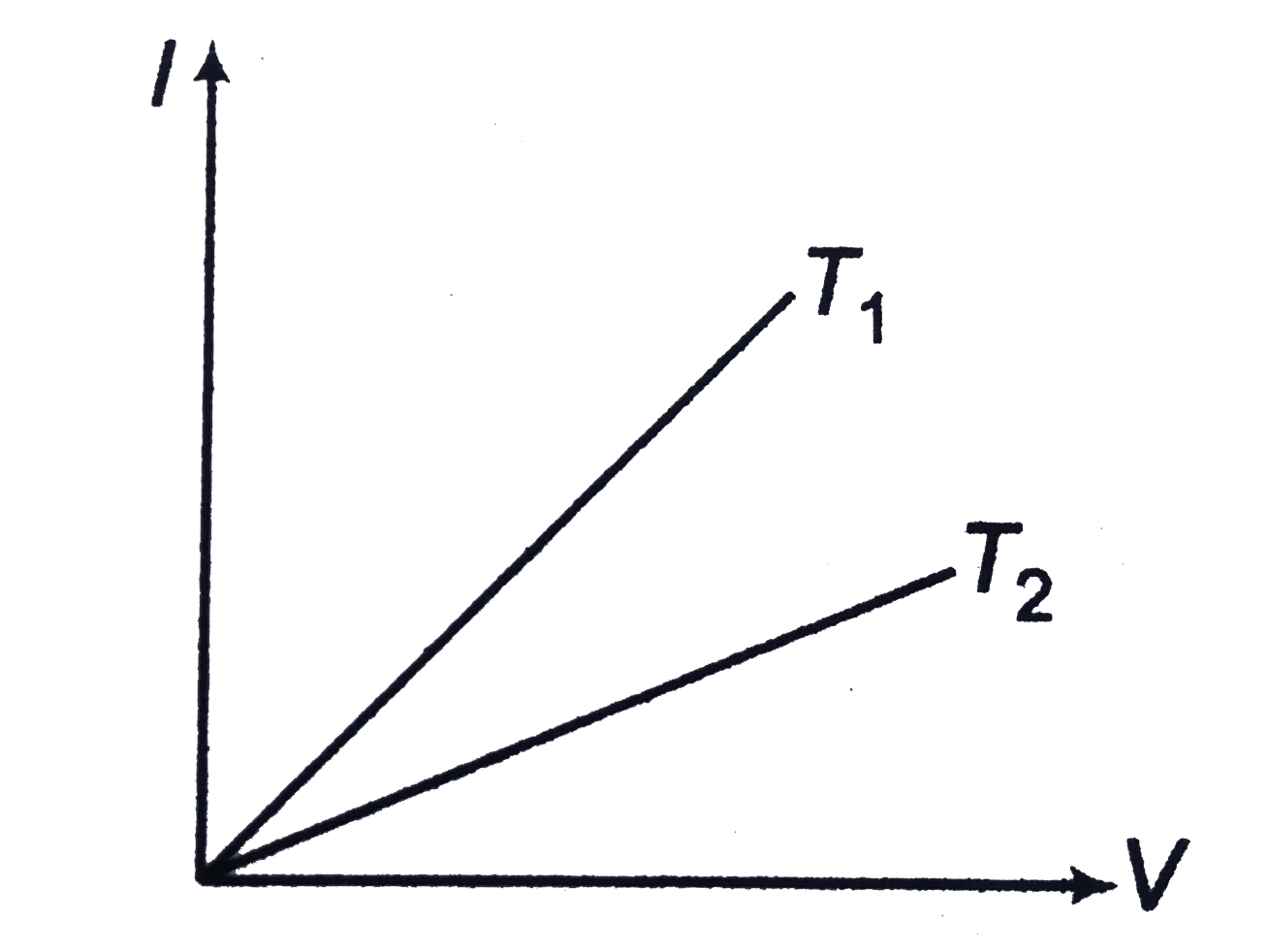
View SolutionThe current voltage graphs for a given metalic wire two different temperature `T_1` and `T_2` are shown in figure The temperature `T_2` is greater than `T_1.` Is this statement true or false?
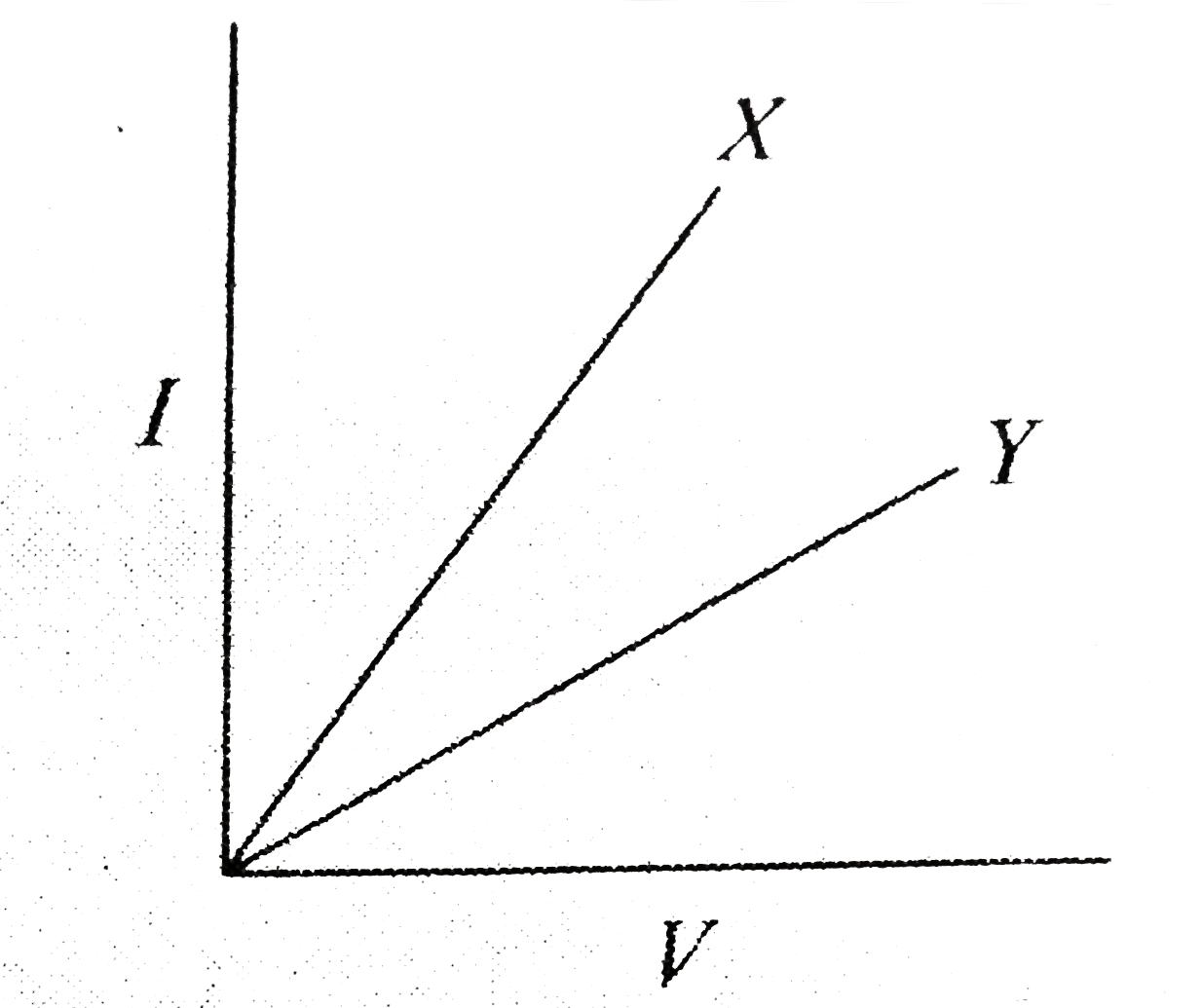
View SolutionThe voltage-current variations of two metallic wire X and Y at constant temperature is shown in fig Assumign that the wires have the same length and the same diameter, explain which of the two wires will have larger resisitivity.
View SolutionA beam contains `2.0xx10^8` doubly charged positive ions per cubic centimeter, all of which are moving toward north with a speed of `1.0xx10^5 ms^(-1)`. (a) what are the magnitude and direction of the current density `vecJ`? (b) can you calculate the total current i in this ion beam? If not what additional informaiton in needed.
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation `J = J_0(1 - (r )/(R ))` where r is the distance from the central axis. Thus, the current density is a maximum `J_0` at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of `J_0` and the conductor 's cross - sectional area `A = piR^2`.
View SolutionShown a conductor of length `l` having a circular cross section. The radius of cross section varies linearly form `a to b`. The resistivity of the material is`(rho)`.Assuming that `b-altltl`,find the resistance of the conductor.

View SolutionIf a copper wire is stretched to make it `0.1%` longer what is the percentage change in its resistance?
View SolutionA copper wire having cross- sectional area of `0.5 mm^2` and a length of 0.1 m is initially at `25^@C` and is thermally insulated form the surrounding. If a current of 10A is set up in this wire, find the time in which the wire will start melting. For copper, resistivity is `1.6xx10^(-8)Omega m`, density is `9,000 kgm^(-3)` and specific heat capacity is `0.09 cal g^(-10)C^(-1).` Melting temperature fo copper is `1075^@C`
View SolutionA copper wire having cross- sectional area of `0.5 mm^2` and a length of ` 0.1 m` is initially at `25^@C` and is thermally insulated form the surrounding. If a current of `10A` is set up in this wire, (a) find the time in which the wire will start melting. (b) What will be the change of resistance with time, if the length of the wire is doubled? For copper, resistivity is `1.6xx10^(-8)Omega m,` density is `9,000 kgm^(-3)` and specific heat capacity is `0.09 cal g^(-1)C^(-1).` Melting temperature of copper is `1075^@C`
View SolutionA conductive wire has resistance of 10 ohm at `0^@C` and `alpha is 1/273^@C`, then determine its resistance at `273^@C`
View SolutionWhat is the drift speed of the conduction electrons in a copper wire with radius r = 900 micrometer when it has a uniform current I = 17mA? Assume that each copper atom contributes one conduction electron to the current and the current density is uniform across the wire's cross section. The density of copper is 9000 kg/m^3 and atomic mass is 63.5u .
View Solution(a) At what temperature would the resistance of a copper conductor be double of its value of `0^(@)C`? (b) Does this same temperature hold for all copper conductors, regardless of shape and size? `[alpha_(c) = 4.0xx10^(-3).^(@)C^(-1)]`
View SolutionA potential difference is applied across the filament of a bulb at t =0, and it is maintained at a constant value while the filament gets heated to its equilibrium temperature. We find that the final current in the filament is one sixth of the current drawn at t = 0. if the temperature of the filament at t = 0 is `20^@C` and the temperature coefficient of resistivity at `20^@C` is `0.0043 ^@C^(-1),` find the final temperature of the filament.
View SolutionThe space between the plates orf a parallel plate capacitor is completely filled with a meterail of resistaivity `2xx10^(11) Omegam` and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the paltes is 20uF. Find the leakage current if a potential difference 2500 V is applied across the capacitor.
View SolutionA uniform copper wire of mass `2.23 xx10^(-3)` kg carries a current of 1 A when 1.7 V is applied across it. Calculate the length and the area of cross section. If the wire is uniformly stretched to double its length, calculate the new resistance. Density of copper is `8.92xx10^3 kgm^(-3)` and resistivity is `1.7xx10^(-8) Omega m.`
View Solution
Exercise 5.1 questions and complete solutions for chapter ELECTRIC CURRENT AND CIRCUIT of CENGAGE PHYSICS (ENGLISH) of Class 12