Complete Solutions to Single Correct Option of chapter NUCLEAR PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEAR PHYSICS |
| CENGAGE PHYSICS | Single Correct Option |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
An element A decays into an element C by a two step process `A to B + ._2He^4` and `B to C + 2e^(-)` .Then,
View SolutionConsider two arbitaray decay equation and mark the correct alternative` s` given below. (i) `._(92)^(230)U rarr n+._(92)^(229)U` (ii)`._(92_^(230)U rarr P +._(91)^(229)Pa`
Given: `M(._(92)^(230)U) =230.033927 u,M(._(92)^(229)U)=229.03349 u, m_(n)=1.008665u`, `M(._(91)^(229)Pa) =229.032089, m_p`=1.007825, 1 am u =931.5 MeV`.
View SolutionIn a smaple of rock, the ration `.^(206)Pb` to `.^(238)U` nulei is found to be `0.5.` The age of the rock is (given half-life of `U^(238)` is `4.5 xx 10^(9)` years).
View SolutionLet `E_(1)` and `E_(2)` be the binding energies of two nuclei `A` and `B`. it is observed that nuclei of `A` combine together to form a `B` nuclus. This observation is correct only if .
View SolutionA radioactive sample decays by `63%` of its initial value in `10s`. It would have decayed by `50%` of its initial value in .
View SolutionA nucleus moving with velocity `bar(v)` emits an `alpha`-particle. Let the velocities of the `alpha`-particle and the remaining nucleus be `bar(v)_(1)` and `bar(v)_(2)` and their masses be `m_(1)` and `(m_2)` then,
View SolutionWhich of the following statements is incorrect for nuclear forces?
View SolutionA certain radioactive material can undergo three constant `lambda,2lambda` and `3 lambda`. Then, the effective decay constant `lambda_(eff)` is equal to `n lambda`. What is the value of n?
View SolutionIn an `alpha` -decay, the kinetic energy of `alpha`-particles is `48 MeV` and `Q` value of the reaction is `50 MeV`. The mass number of the mother nucleus is (assume that daughter nucleus is in ground state)
View SolutionA sample of radioactive material decays simultaneouly by two processes A and B with half-lives `(1)/(2)` and `(1)/(4)h`, respectively. For the first half hour it decays with the process A, next one hour with the proecess B, and for further half an hour with both A and B. If, origianlly, there were `N_0` nuceli, find the number of nuclei after 2 h of such decay.
View SolutionIn which of the following processes, the number of protons in the nuleus increase ?
View SolutionA radioactiev nuleus `X` deays to a stable nuleus `Y`. Then, time graph of rate of formation of `Y` against time `t` will be:
View SolutionA heavy nuleus having mass number `200` gets disintegrated into two small fragmnets of mass numbers `80` and `120`. If binding energy per nulceon for parent atom is `6.5 MeV` and for daughter nuceli is `7 MeV` and `8 MeV`, respectivley , then the energy released in the decay will be.
View SolutionAn element` X` decays , first by positron emission and then two `alpha`-particles are emitted in successive radiactive decay. If the product nucleus has a mass number `229` and atomic number `89`, the mass number and atomic number of element ` X` are.
View Solution90% of a radioactive sample is left undecayed after time t has elapsed. What percentage of the initial sample will decay in a total time 2t
View SolutionA radioactive element X converts into another stable element. Y half-life X is 2 h Initially only X is present. After time t, the ratio of atoms of X and Y is found to be `1:4` then t in hour is
View SolutionA radioactive element P disintegrates into Q which further disintegrates into R as shown in figure.
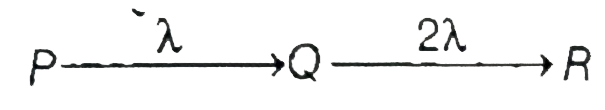
At t=0, number of nuclei of P, Q and R are `N_(0)` 0 and 0. At time t number of nuclei of P,Q and R are `N_(1) , N_(2)` and `N_(3)` respectively . The ratio of `N_(1)` to `N_(2)` maximum is K Find the value of K.
View SolutionThe binding energy of an electron in the ground state of He is equal to 24.6eV. The energy required to remove both the electron is
View SolutionThe mean life time of a radionuclide, if the activity decrease by `4%` for every `1 h`, would b e(product is non-radioactive, i.e., stable )
View SolutionOn an average, a neutron loses half of its energy per collision with a quesi-free proton. To reduce a `2 MeV` neutron to a thermal neutron having energy `0.04 eV`, the number of collisions requaired is nearly .
View SolutionMasses of two isobars `._(29)Cu^(64)` and `._(30)Zn^(64)` are `63.9298 u` and `63.9292 u`, respectively. It can be concluded from these data that .
View SolutionIf a nucleus such as `.^(226)Ra` that is initially at rest undergoes `alpha`- decay , then which of the following statemnets is true?
View SolutionIf the` Q` value of an endothermic reaction is `11.32 MeV`, then the minimum energy of the reactant nuclei to carry out the reaction is (in laboratotry frame of reference)
View Solution1.00 kg of `.^(235)U` undergoes fission process. If energy released per event is `200 MeV`, then the total energy released is
View SolutionMark out the incoreect statemnet.
View Solution`U-235` can decay by many ways , let us here consider only two ways, `A` and `B`. In decay of `U-235` by means of `A`, the energy released per fission is `210 MeV` while in `B` it is `186 MeV`. Then , the uranium `235` sample is more likely to decay by .
View SolutionA radio isotope `X` with a half life `1.4xx10^(9)` yr decays of `Y` which is stable. A sample of the rock from a cave was found to contain `X` and `Y` in the ratio `1:7`. The age of the rock is
View SolutionWhat is the probability of a radioactive nucleus to survive one mean life?
View SolutionConsider one of fission reactions of `^(235)U` by thermal neutrons `._(92)^(235)U +n rarr ._(38)^(94)Sr +._(54)^(140)Xe+2n` . The fission fragments are however unstable and they undergo successive `beta`-decay until `._(38)^(94)Sr` becomes `._(40)^(94)Zr` and `._(54)^(140)Xe` becomes `._(58)^(140)Ce`. The energy released in this process is
Given: `m(.^(235)U) =235.439u,m(n)=1.00866 u, m(.^(94)Zr)=93.9064 u, m(.^(140)Ce) =139.9055 u,1u=931 MeV]` .
View SolutionA star initially has `10^40` deuterons. It produces energy via the processes `._1^2H+_1^2Hrarr_1^3H+p` and `._1^2H+_1^3Hrarr_2^4He+n`, where the masses of the nuclei are
`m(.^2H)=2.014` amu, `m(p)=1.007` amu, `m(n)=1.008` amu and `m(.^4He)=4.001` amu. If the average power radiated by the star is `10^16 W`, the deuteron supply of the star is exhausted in a time of the order of
View SolutionTwo radioactive materials `X_1` and `X_2` have decay constants `10 lambda` and `lambda`, respectively. If initialy they have the same number of nuclei, then the ratio of the number of nuclei of `X_1` to that of `X_2` will be `1//e` after a time
(a) `1//10 lambda` (b) `1//11 lambda` (c) `11//10lambda` (d) `1//9lambda`
View SolutionA radioactive substance is being produced at a constant rate of 200 muclei/s The decay constant of the substance is `1 s^(-1)` After what tiem the number of radioactive nuclie will become 100 ? Initially there are no nuclei present.
View SolutionA radioactive isotope is being produced at a constant rate X Half-life of the radioactive substance is Y After some time the number of radiactive nuclie become constant The value of this constant is
View SolutionA radioactive substance X decays into another radioactive substance Y Initially only X was present. `lambda_(x)` and `lambday_(y)` are the disnttegration constants of Xa nd Y `N_(x)` and `N_(y)` are the number of nuclie of X and Y at any time t. Number of nuclei `N_(y)` will be maximum when
View SolutionThere are two radioactive nuclei A and B A is an alpha emitter and B a beta emitter. Their disintegration constants are in the ratio of atoms of A and B at any time t so that probilities of getting alpha and beta particles are same at that instant?
View SolutionHalf-life of a radioactive sunstance A is two times the half-life of another radioactive substance B Intilally the number of nuclie of A and B are `N_(A)` and `N_(B)` respectively After three half lives of A number of nuclie of bothe equal. Then the ratio `N_(A)//N_(B)` is
View SolutionThere are two radioactive sunstances A and B Decay constant of B is two times that of A Intially bothe have equal number of nuclei. After n half lives of A rate of disintegration of both are equla. The value of n is
View SolutionA radioactive ncleus A finaly transforms into a stable nucleus. B Then A and B can be
View SolutionIf `92^(U^(238))` changes to `85^(At^(210))` by a series of `alpha` and `beta` decays, the number of `alpha` and `beta` decays undergone is
View SolutionNumber jof nuclei of radioactive substance at time t=0 are 1000 and 9000 at time t=2 s. Then number of nuclie at time t=4 s will be
View SolutionA rodiactive nucleus is being produced at a constant rate `alpha` per second Its decay constant is `lambda` If `N_(0)` are the number of nuclie at tieme t=O then, maximum number of nuclei possible are
View SolutionIn a sample of radioactive material , what fraction of the initial number of active nuclei will remain undisintegrated after half of the half life of the sample ?
View SolutionThe activity of a radioactive substance is `R_(1)` at time `t_(1)` jand `R_(2)` at time `t_(2)(gt t_(1))` its decay constant is `lambda` Then
View SolutionThe activity of a radioactive susbtance is `R_(1)` at time `t_(1)` and `R_(2)` at time `t_(2)`(>t1). its decay constant is λ. Then, number of atoms decayed between time interval `t_(1)` and `t_(2)` are
View SolutionThe ratio of molecules mass of two radiactive substances is `(3)/(2)` and the ratio of their decay constant is `(4)/(3)` Then the ratio of their intial activity per mol will be
View Solution`N_(1)` atoms of a radioactive element emit `N_(2)` "beta" particles per second The decay constant of the element is (in` s^(-1))`
View SolutionThe binding energies of nuclei X and Y are `E_(1)` and `E_(2)` respectivley . Two atoms of X fuse to give one atom of Y and an energy Q is released. Then
View SolutionBinding energy per nucleon of `1^(H^(2))` and `2^(He^(2))` are 1.1 MeV and `7.0` respectively Energy realsed in the process `1^(H^(2))+1^(He^(4))` is
View Solution`._(92)U^(238)` absorbs a neutron. The product emits an electron. This product further emits an electron. The result is
View SolutionThe activity of a radioative element decreases to one third of the original activity `I_(0)` in a period of nine years. After a further 1apse of nine years, its activity will be
View SolutionThe half-life of a radioactive decay is x times its mean life. The value of zx is
View SolutionNeutron decay in the free space is given follows:
`._0n^1 rarr. _1H^1 +._(-e)^0 +[]`
Then, the parenthesis represents
View SolutionA nucleus `._Z^AX ` emits an `alpha`-particel. The resultant nucleus emits a `beta^(+)` particle. The respective atomic and mass numbers of the final nucleus will be
View SolutionCertain radioactive substance reduces to 25% of its value in 16 days. Its half-life is
View SolutionWhat is the age of an ancient wooden piece if it is known that the specific activity of `C^(14)` nuclide in it amouts to `3//5` of that in fresh trees? Given: the half of `C` nuclide is `5570 years` and `log_(e)(5//3)=0.5` .
View SolutionA helium atom, a hydrogen atom and a neutron have mases of` 4.003 u, 1.008 u` and `1.009 u` (unified atomic mass units), respectively. Assuming that hydogen atoms and neutrons can be fuse to from helium, what is the binding energy of a helium nucleus?
View SolutionA certain radioactive element has half-life of `4` days. The fraction of material that decays in `2 `days is
View SolutionIn the disintegration series
`._(92)^(238)U overset rarr (alpha) X overset rarr (beta^(-))._Z^(A)Y` the values of `Z` and `A`, respectively, will be
View SolutionAtomic mass number of an element is `232` and its atomic number is `90`. The end product of this radiaoctive element is an isotope of lead (atomic mass `208` and atomic number `82`.) The number of `alpha`-and `beta` -particles emitted are.
View SolutionThe initial activity of a certain radioactive iostope was measured as `16000` counts `min.^(-1)`. Given that the only activity measured was due to this isotaope and that its activity after `12 h` was `2100` counts `min.^(-1)`, its half-life, in hours, is nearest to [Given `log_(e) (7.2)=2`].
View SolutionThe minimum frequency of a `gamma`-ray that causes a deutron to disintegrate into a poton and a neutron is `(m_(d)=2.0141 am u, m_p=1.0078 am u, m_n=1.0087 am u.)`.
View SolutionThe fission of a heavy nucleus gives, in general, two smaller nuclei, two or three neutrons, some `beta-`particles and some `gamma-`radiation. It is always true that the nuclei produced.
View SolutionThe activity of a radioactive sample is `1.6` curie, and its half-life is `2.5 days`. Its activity after `10 days` will be
View SolutionThe rest mass of the deutron `._(1)^(2)` H is equivalent ot an energy of 1876 MeV the rest mass of a proton is equivalent to 939 MeV and that of a neutrom is 940 MeV A deuteron may disintegrate to proton and neutron if it :
View SolutionA newly prepared radioactive nuclide has a decay constant `lambda` of `10^(-6) s^(-1)`. What is the approximate half-life of the nuclide?
View SolutionThe half-life of a certain radioactive isotope is `32 h`.What fraction of a sample would ramain after `16h`?
View SolutionSamples of two radioactive nuclides, `X` and `Y`, each have equal activity `A` at time `t=0`. X has a half-life of `24 years` and `Y` a half-life of `16 years`. The samples are mixed together. What will be the total activity of the mixture at `t=48` years?
View SolutionA sample of radioactive element has a mass of `10 g` at an instant `t=0`. The approximate mass of this element in the sample after two mean lives is
View SolutionIn the case of thorium `(A=232 and Z=90)`, we obtain an isotope of lead `(A=208 and Z=82)` after some radioactive disintegrations. The number of `alpha`- and `beta`-particles emitted are, respectively,
View SolutionAfter an interval of one day , `1//16th` initial amount of a radioactive material remains in a sample. Then, its half-life is .
View SolutionThe half-life of `.^215At` is `100mus`. The time taken for the activity of a sample of `.^215At` to decay to `1/16th` of its initial value is
View SolutionA stationary thorium nucleus `(A=200 , Z=90)` emits an alpha particle with kinetic energy `E_(alpha)`. What is the kinetic energy of the recoiling nucleus
View SolutionThe fraction of a radioactive material which reamins active after time t is `9//16`. The fraction which remains active after time `t//2` will be .
View SolutionThe radioactive decay rate of a radioactive element is found to be `10^(3) ` disintegration per second at a certain time . If the half life of the element is one second , the decay rate after one second is?
View SolutionThe percentage of quantity of a radioactive material that remains after 5 half-lives will be .
View Solution`.^(238)U` decays with a half-life of `4.5 xx10^(9)` years, the decay series eventually ending at `.^(206)Pb`, which is stable. `A` rock sample analysis shows that the ratio of the number of atoms of `.^(206)Pb` to `.^(238)U` is 0.0058. Assuming that all the `.^(206)Pb` is produced by the decay of `.^(238)U` and that all other half-lives on the chain are negligible, the age of the rock sample is `(ln 1.0058 =5.78 xx10^(-3))`.
View SolutionA radioactive nucleus undergoes a series of deacy according to the scheme.
`Aoverset(alpha)rarrA_(1)overset(beta^(-))rarrA_(2)overset(alpha)rarrA_(3)overset(gamma)rarrA_(4)`
If the mass number and atomic number of `A` are `180` and `72` respectively, what are these numbers for `A_(4)`.
View SolutionIf `10%` of a radioactive substance decays in every 5 year, then the percentage of the substance that will have decaed in `20 years` will be .
View SolutionStationary nucleus `._(92)^(238)U` decays by a emission generating a total kinetic energy T:
`._(92)^(238)U rarr ._(90)^(234)Th +._2^4 alpha`
What is the kinetic energy of the `alpha`-particle?
View SolutionThe activity of a radioactive elemment decreses to oen-third of the original activity `A_(0)` in a period of `9` years. After a further lapse of `9` years, its acticity will be
View SolutionThe half-life period of RaB`(._(82)Pb^(214))` is `26.8 min`. The mass of one curie of RaB is
View SolutionA `5 xx 10^(-4) Å` photon produces an electron-positron pair in the vincinity of a heavy nucleus. Rest energy of electron is `0.511 MeV`. sIf they have the same kinetic energies, the energy of each paricles is nearly
View SolutionA freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. The minimum time after which it would be possible to work safely with this source is
View SolutionUranium ores contain one radium `-226 `atom for every `2.8 xx 10^(6)` uranium `-238` atoms. Calculate the half-life of `._(88)Ra^(226)` is `1600` years `(._(88)Ra^(226)` is a decay product of `._(92)U^(238))`.
View SolutionPlutonium has atomic mass `210` and a decay constant equal to `5.8 xx 10^(-8)s^(-1)`. The number of `alpha`-particles emitted per second by `1 mg` plutonium is
(Avogadro's constant =` 6.0 xx 10^(23)`).
View SolutionAt any instant, the ratio of the amount of radioactive substance is 2 : 1. If their half-lives be respectively, 12 h and 16 h then after 2 days, what will be the ratio of the substances?
View SolutionRadioactivity of a sample at `T_(1)` time is `R_(1)` and at time `T_(2)` is `R_(2).` If half-life of sample is T, then in time `(T_(2)-T_(1)),` the number of decayed atoms is proportional to
View SolutionHalf-lives of two radioactive substances `A` and `B` are respectively `20` min and `40` min. Initially, the samples of `A` and `B` have equal number of nuclei. After `80` min the raatio of remaining number of `A` and `B` nuclei is
View SolutionA radioactive nucleus can decay by two differnet processess. The mean value period for the first process is `t_(1)` and that the second process is `t_(2)` .The effective mean value period for the two processes is .
View SolutionThe half-life of radium is `1620 years` and its atomic weight is `226`. The number of atoms that will decay from its `1 g` sample per second will be .
View SolutionThe nuclear radius of a nucelus with nucleon number `16` is `3 xx 10^(-15) m`. Then, the nuclear radius of a nucleus with nucleon number `128` is .
View SolutionThe nuclear radius of `._(8)O^(16)` is `3 xx10^(-15) m`. If an atomic mass unit is `1.67 xx 10^(-27) kg`, then the nuclear density is approximately.
View SolutionWhat would be the energy required to dissociate completely `1 g` of `Ca-40` into its constituent, particles? Given: Mass of proton `=1.00866 am u`,
Mass of neutron `=1.00866 am u`,
Mass of `Ca-40 =39.97454 am u`, (Take `1 am u =931 MeV`).
View SolutionIn fission,the percentage of mass converted into energy is about
View SolutionIn the nuclear raction `._1H^2 +._1H^2 rarr ._2He^3 +._0n^1` if the mass of the deuterium atom `=2.014741 am u`, mass of `._2He^3` atom `=3.016977 am u`, and mass of neutron `=1.008987 am u`, then the `Q` value of the reaction is nearly .
View SolutionAssuming that about 20 MeV of energy is released per fusion reaction
`1^(H^(2))+1^(H^(2))to2^(He^(4))`
then the mass `1^(H^(2))`consumed per day in a jfusion rector of power 1 MW wll apporximately be :
View SolutionAssuming that about 200g MeV energy is released per fission of `""_(92)U^(235)` nuclei. What would be the mass of `U^(235)` consumed per day in the fission of reactor of power 1 MW approximately?
View SolutionIf mass of `U^(235)=235.12142 a.m.u.`, mass of `U^(236) =236.1205 amu`, and mass of neutron `=1.008665 am u`, then the energy required to remove one neutron from the nucleus of `U^(236)` is nearly about.
View SolutionBinding energy per nucleon of `1^(H^(2))` and `2^(He^(2))` are 1.1 MeV and `7.0` respectively Energy realsed in the process `1^(H^(2))+1^(He^(4))` is
View Solutionin the fusion reaction `""_(1)H^(2)+""_(1)H^(2)to ""_(2)He^(3) +""_(0)N^(1),` are masses of deuteron and neutron expressed in amu are 2.015, 3.017 and 1.0009, respectively , if 1 kg of deuterium undergoes complete fusion , then find the amount of total energy released .
1 amu = 931.5 ME V/`c^(2)`.
View Solution
Single Correct Option questions and complete solutions for chapter NUCLEAR PHYSICS of CENGAGE PHYSICS (ENGLISH) of Class 12