Complete Solutions to Comprehension Type of chapter MISCELLANEOUS VOLUME 3 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MISCELLANEOUS VOLUME 3 |
| CENGAGE PHYSICS | Comprehension Type |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
We know that electric field (E ) at any point in space can be calculated using the relation
`vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk`

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as `V = 2x^2`, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
`vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk`

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as `V = 2x^2`, where x is in meter. Its variation is as shown in figure
A charge particle of mass 10 mg and charge `2.5 muC` is released from rest at `x = 2 m`. Find its velocity when it crosses origin.
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
`vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk`

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as `V = 2x^2`, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.
View SolutionConsider a system of two equal points charges, each `Q = 8 muC`, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge `mu` is held at a point (0,0.1m) on the y-axis. Mass of the charge `mu` is 91 mg . At t= 0 , `mu` is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is ` 9 xx 10^(-3)N`.
Charge q is
View SolutionConsider a system of two equal points charges, each `Q = 8 muC`, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge `mu` is held at a point (0,0.1m) on the y-axis. Mass of the charge `mu` is 91 mg . At t= 0 , `mu` is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is ` 9 xx 10^(-3)N`.
Amplitude of motion is
View SolutionConsider a system of two equal points charges, each `Q = 8 muC`, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge `mu` is held at a point (0,0.1m) on the y-axis. Mass of the charge `mu` is 91 mg . At t= 0 , `mu` is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is ` 9 xx 10^(-3)N`.
Frequency of oscillation is
View SolutionConsider a system of two equal points charges, each `Q = 8 muC`, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge `mu` is held at a point (0,0.1m) on the y-axis. Mass of the charge `mu` is 91 mg . At t= 0 , `mu` is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is ` 9 xx 10^(-3)N`.
Equation of SHM (displacement from mean position) can be expressed as
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was `10^(3) ms^(-1) and 2 xx 10^(3) ms^(-1)` for first and second particle, respectively, and mass of these particles were `2 xx 10^(-30) kg and 10^(-30)kg`, respectively. Distance between them were 12Å(1Å = 10^(-`10)m).`
Acceleration of the first particle was
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was `10^(3) ms^(-1) and 2 xx 10^(3) ms^(-1)` for first and second particle, respectively, and mass of these particles were `2 xx 10^(-30) kg and 10^(-30)kg`, respectively. Distance between them were 12Å(1Å = 10^(-`10)m).`
Acceleration of the second particle was
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was `10^(3) ms^(-1) and 2 xx 10^(3) ms^(-1)` for first and second particle, respectively, and mass of these particles were `2 xx 10^(-30) kg and 10^(-30)kg`, respectively. Distance between them were 12Å(1Å = 10^(-`10)m).`
if the first particle is stopped for a moment and then released, the velocity of center of mass of the system just after the release will be
View SolutionIn a certain experiments to measure the ratio of charge to mass of elementry particles, a surprising result was obtained in which two particle, a surprising result was obtained in which two particles moved in such a way that the distance between them always remained constant. It was also noticed that this two-particle system was isolated from all other particles and no force was acting on this system except the force between these two mases. After careful observation followed bu intensive calculation, it was deduced that velocity of these two particles was always opposite in direction and magnitude of velocity was `10^(3) ms^(-1) and 2 xx 10^(3) ms^(-1)` for first and second particle, respectively, and mass of these particles were `2 xx 10^(-30) kg and 10^(-30)kg`, respectively. Distance between them were 12Å(1Å = 10^(-`10)m).`
Paths of the two particles was
View SolutionIn the circuit shown in figure initially the switch is opened. The switch is closed now.
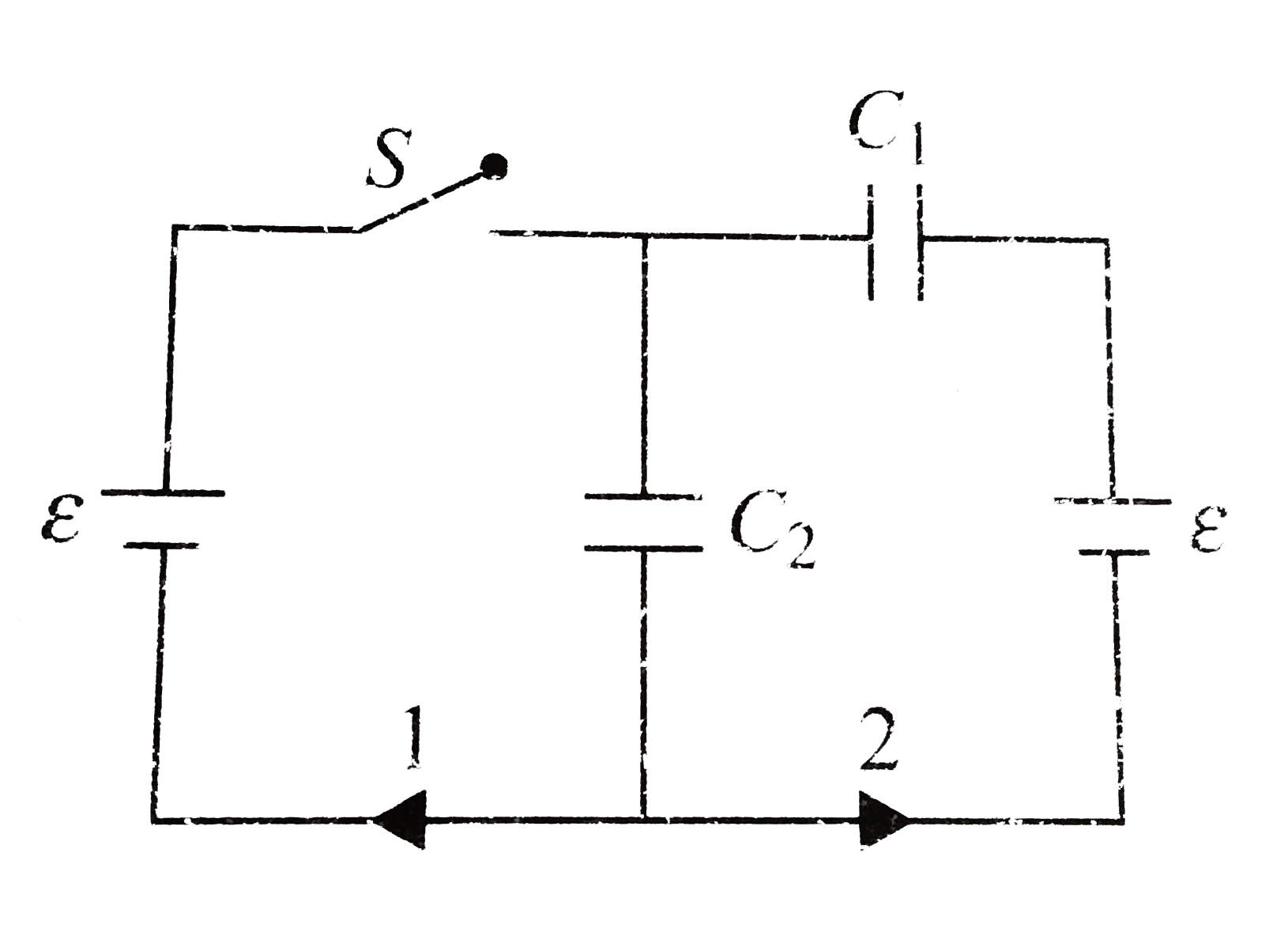
The charge that will flow in direction 1 is
View SolutionIn the circuit shown in figure initially the switch is opened. The switch is closed now.

The charge that will flow in direction 2 is
View SolutionCapacitor `C_1 = 2 muF and C_2 = 3muF` are connected in series to a battery of emf `epsilon= 120 V` whose midpoint is earthed. The wire connecting the capacitors can be earthed through a key K. Now, key K is closed. Determine the charge flowing through the sections 1, 2, and 3 in the directions indicated in figure
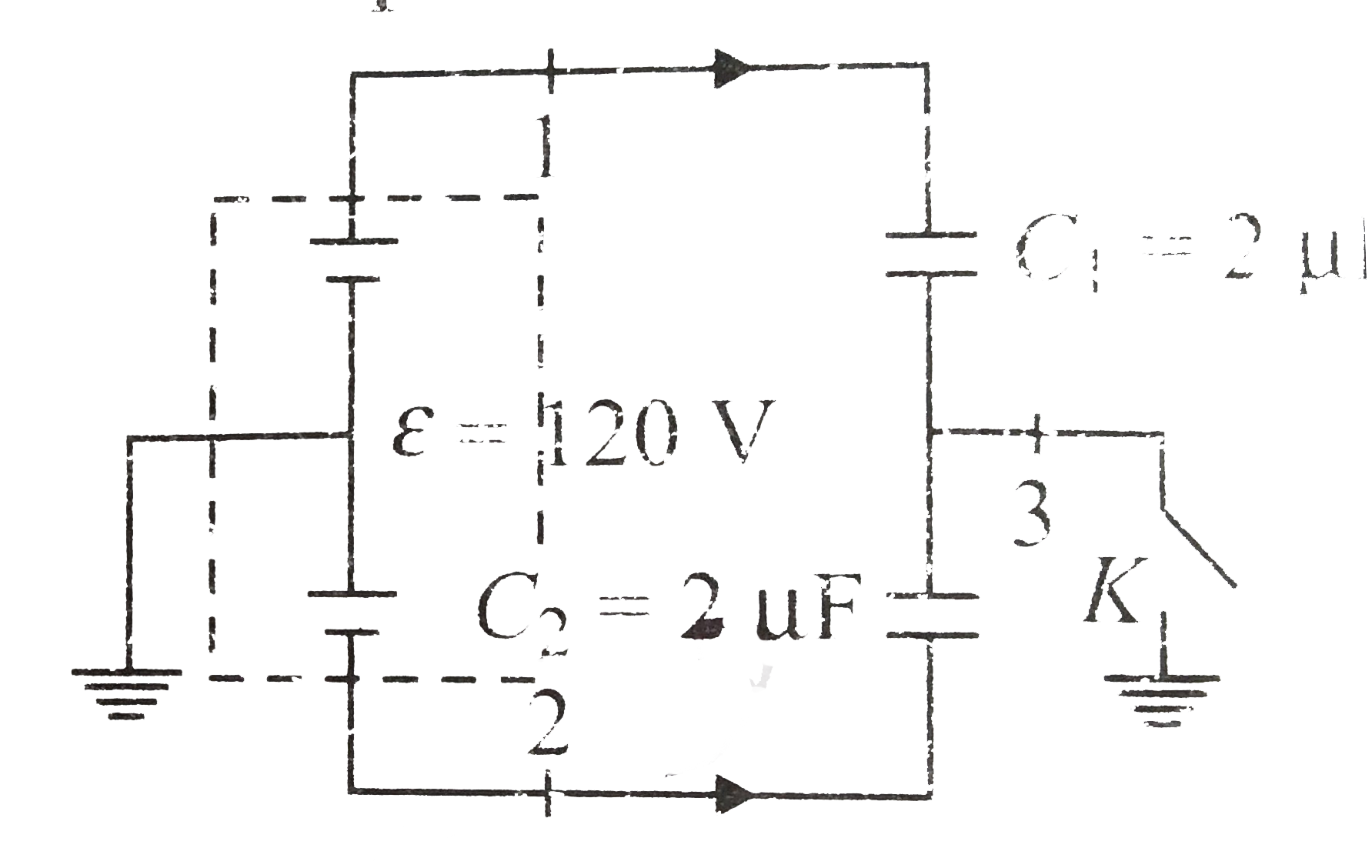
In section 2,
View SolutionCapacitor `C_1 = 2 muF and C_2 = 3muF` are connected in series to a battery of emf `epsilon= 120 V` whose midpoint is earthed. The wire connecting the capacitors can be earthed through a key K. Now, key K is closed. Determine the charge flowing through the sections 1, 2, and 3 in the directions indicated in figure

In section 2,
View SolutionCapacitor `C_1 = 2 muF and C_2 = 3muF` are connected in series to a battery of emf `epsilon= 120 V` whose midpoint is earthed. The wire connecting the capacitors can be earthed through a key K. Now, key K is closed. Determine the charge flowing through the sections 1, 2, and 3 in the directions indicated in figure

In section 3,
View SolutionA researcher studying the properties of ions in the upper atmosphere wishes to construct an apparatus with the following charateristics: Using an electric field, a beam of ions, each having charge q, mass m , and initial velocity `vhati`, is turned through an angle of `90^@` as each ion undergoes displacement `Rhati + Rhatj`. The ions enter a chamber as shown in figure and leave through the exit port with the same speed they had when they entered the chamber. The electric field acting on the ions is to have constant magnitude.

Suppose the electric field is produced by two concentric cylindrical electrodes not shown in the diagram, and hence is radial. What magnitude should the field have?
View SolutionA researcher studying the properties of ions in the upper atmosphere wishes to construct an apparatus with the following charateristics: Using an electric field, a beam of ions, each having charge q, mass m , and initial velocity `vhati`, is turned through an angle of `90^@` as each ion undergoes displacement `Rhati + Rhatj`. The ions enter a chamber as shown in figure and leave through the exit port with the same speed they had when they entered the chamber. The electric field acting on the ions is to have constant magnitude.

If the field is produced by two flat plates and is uniform in direction, what value should the field have in this case?
View SolutionA point charge `q_1` is placed inside cavity 1 and another point charge `q_2` is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.

The charge on outer surface of the conductor would be
View SolutionA point charge `q_1` is placed inside cavity 1 and another point charge `q_2` is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
`vecE` inside the conductor at point S distant r from point charge q, due to charge on outer surface of the conductor, would be
View SolutionA point charge `q_1` is placed inside cavity 1 and another point charge `q_2` is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
`vecE` inside the conductor at point S distant r from point charge q, due to charge on outer surface of the conductor, would be
View SolutionA point charge `q_1` is placed inside cavity 1 and another point charge `q_2` is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
If charge `q_2` is at point Q (inside cavity 2), then `vecE` at the center of cavity 2 due to induced charge on the surface of cavity 2 would be
View SolutionA point charge `q_1` is placed inside cavity 1 and another point charge `q_2` is inside cavity 2. A point charge q is placed outside the conductor. For the situation described above, answer the following questions.
If the potential of the conductor is `V_0` and charge `q_2` is placed at the center of cavity 2, then potential at point Q is
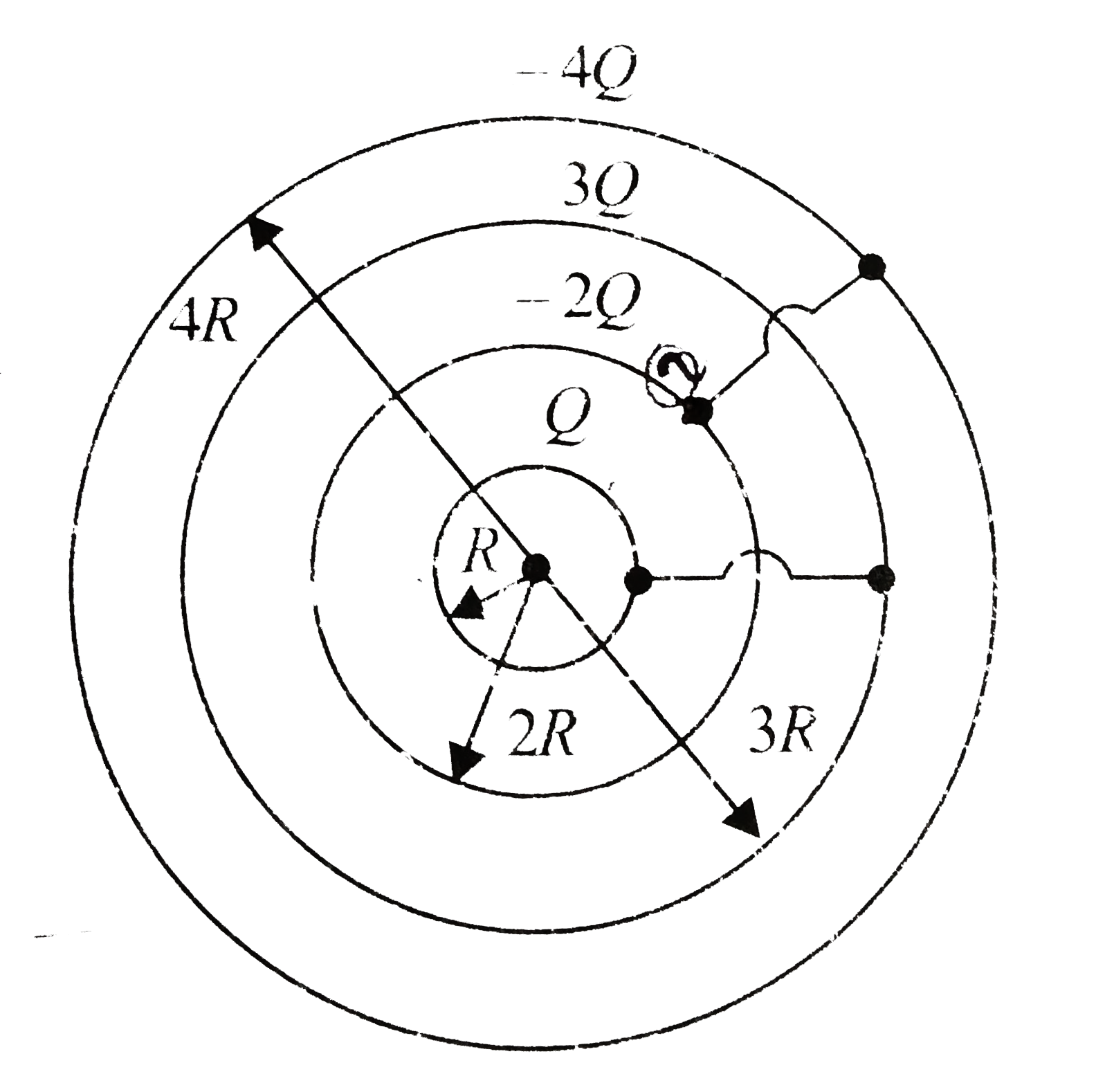
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.)
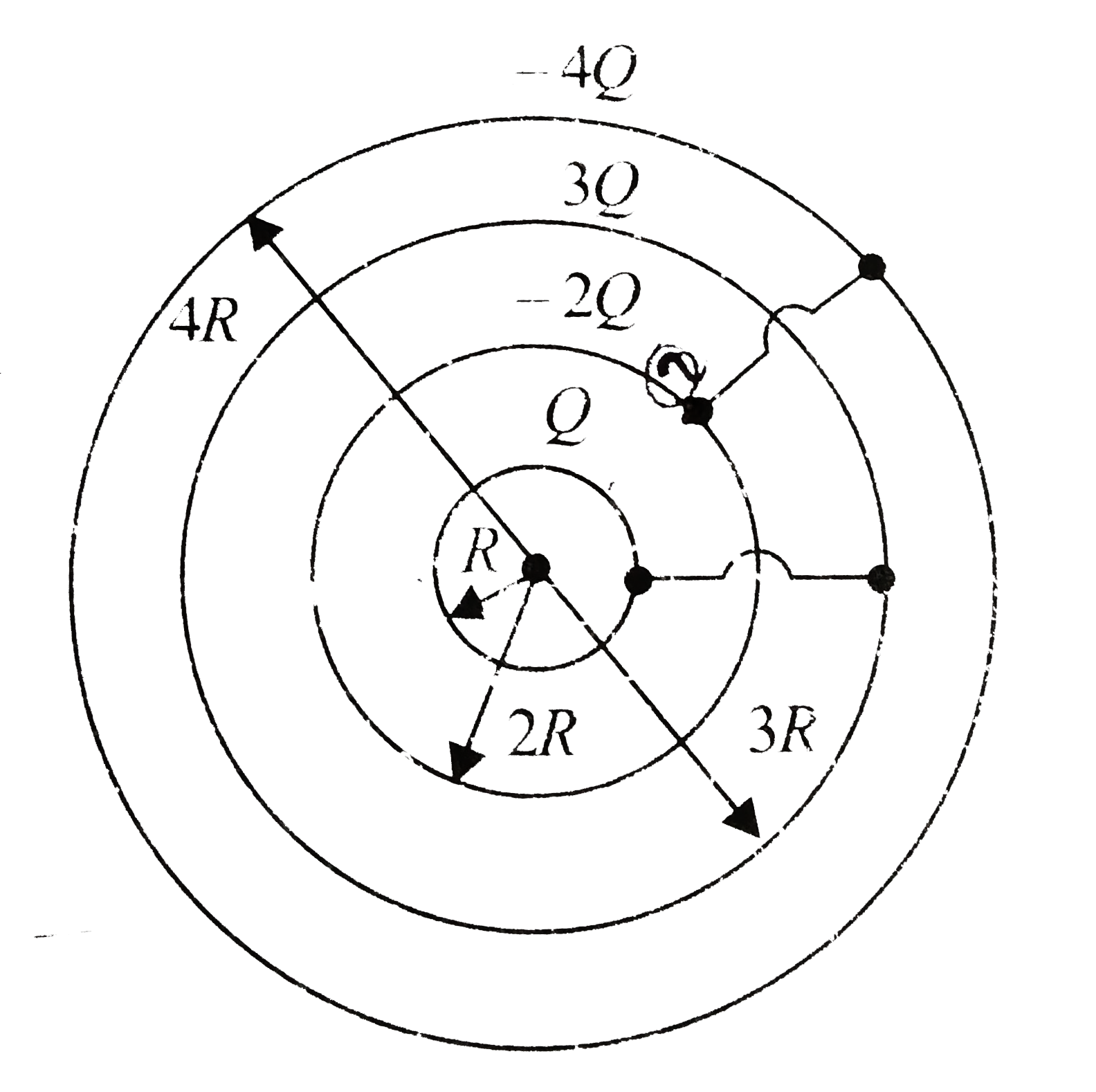 ,
,
The charge on the inner surface of the third conductor is
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.). The final charge on conductor 4 is-
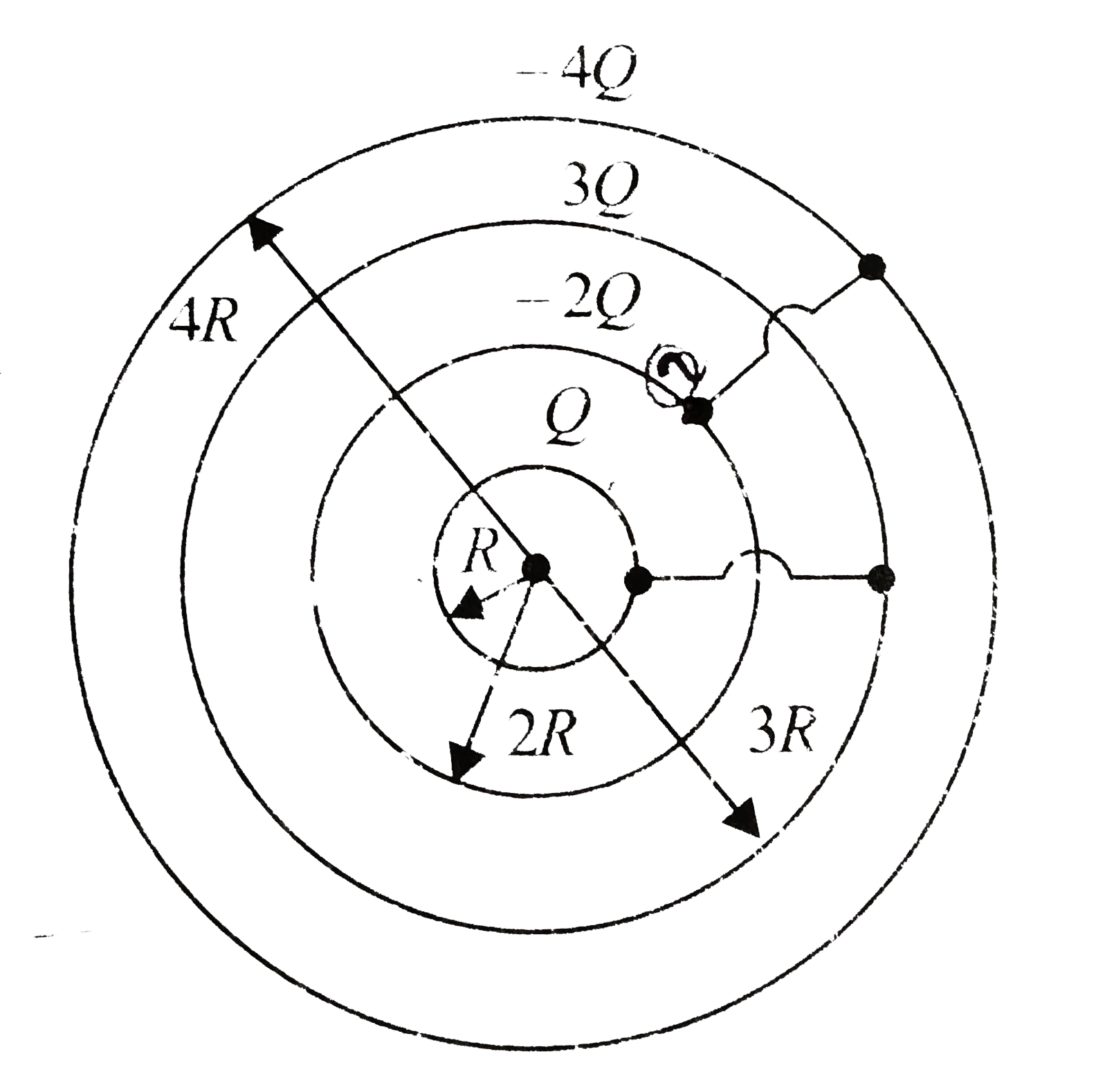
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.)
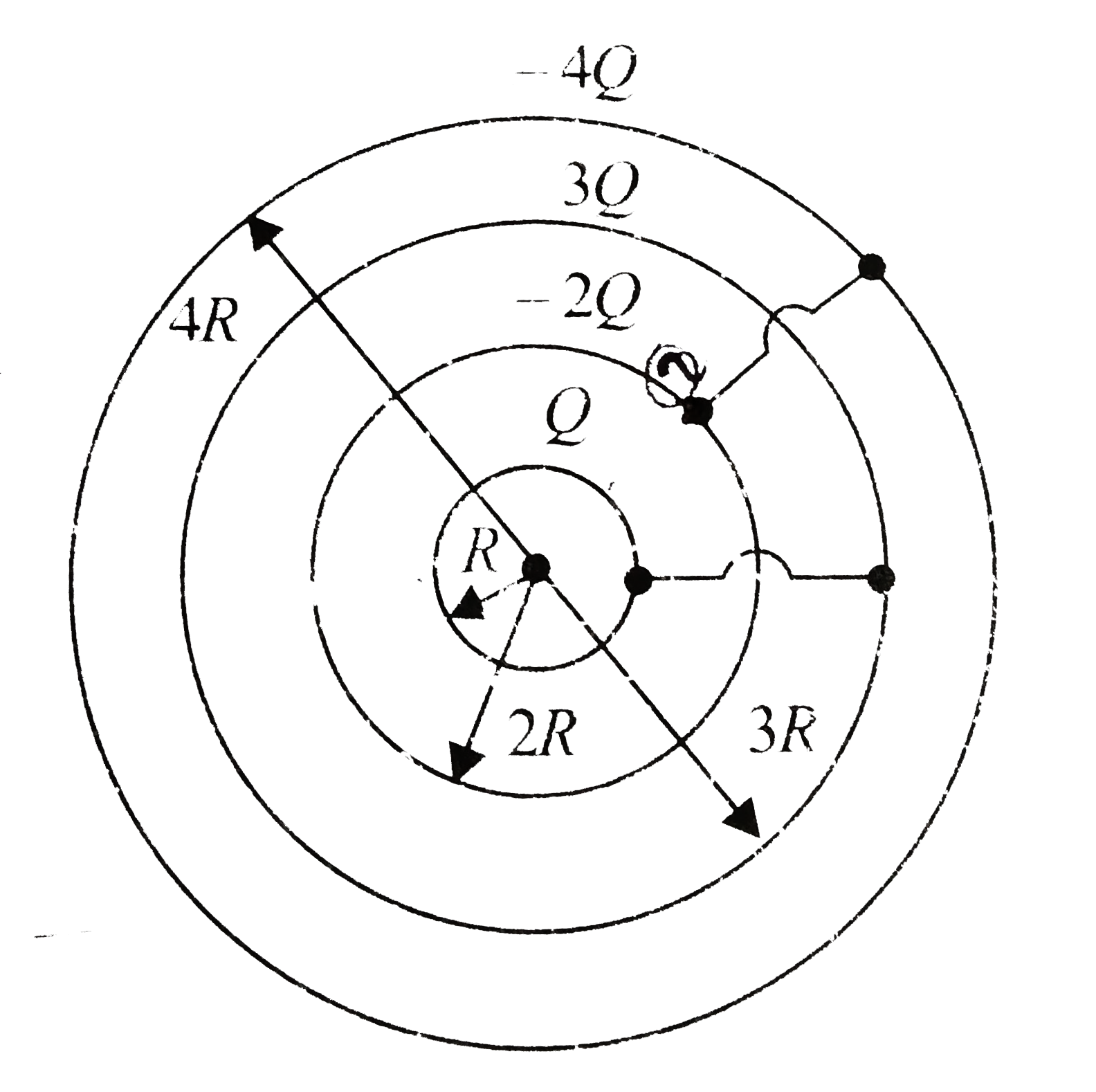
View SolutionFour concentric hollow spheres of radii R, 2R, 3R, and 4R are given the charges as shown in figure. Then the conductors 1 and 3, 2 and 4 are connected by conducting wires (both the connections are made at the same time.) .find thr potential of last sphere
View SolutionThree metallic plates out of which the middle is given charge Q as shown in the figure. The outer plates can be earthed with the help of switches `S_1 and S_2` . The area of each plates is the same. Answer the following question based on the given passage.
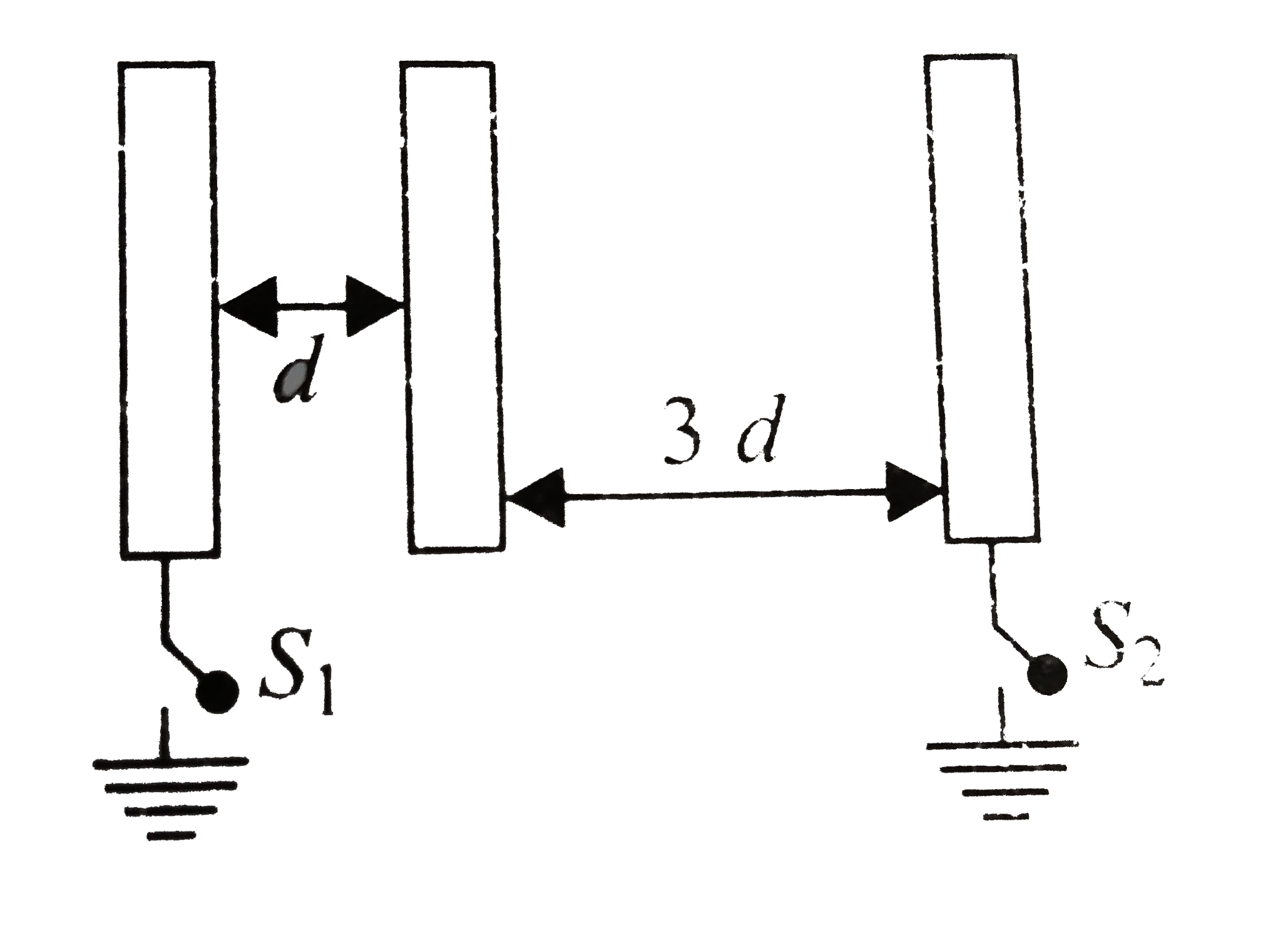 ,brgt The charge appearing on the outer surface of extreme left plate is
,brgt The charge appearing on the outer surface of extreme left plate is
View SolutionThree metallic plates out of which the middle is given charge Q as shown in the figure. The outer plates can be earthed with the help of switches `S_1 and S_2` . The area of each plates is the same. Answer the following question based on the given passage.
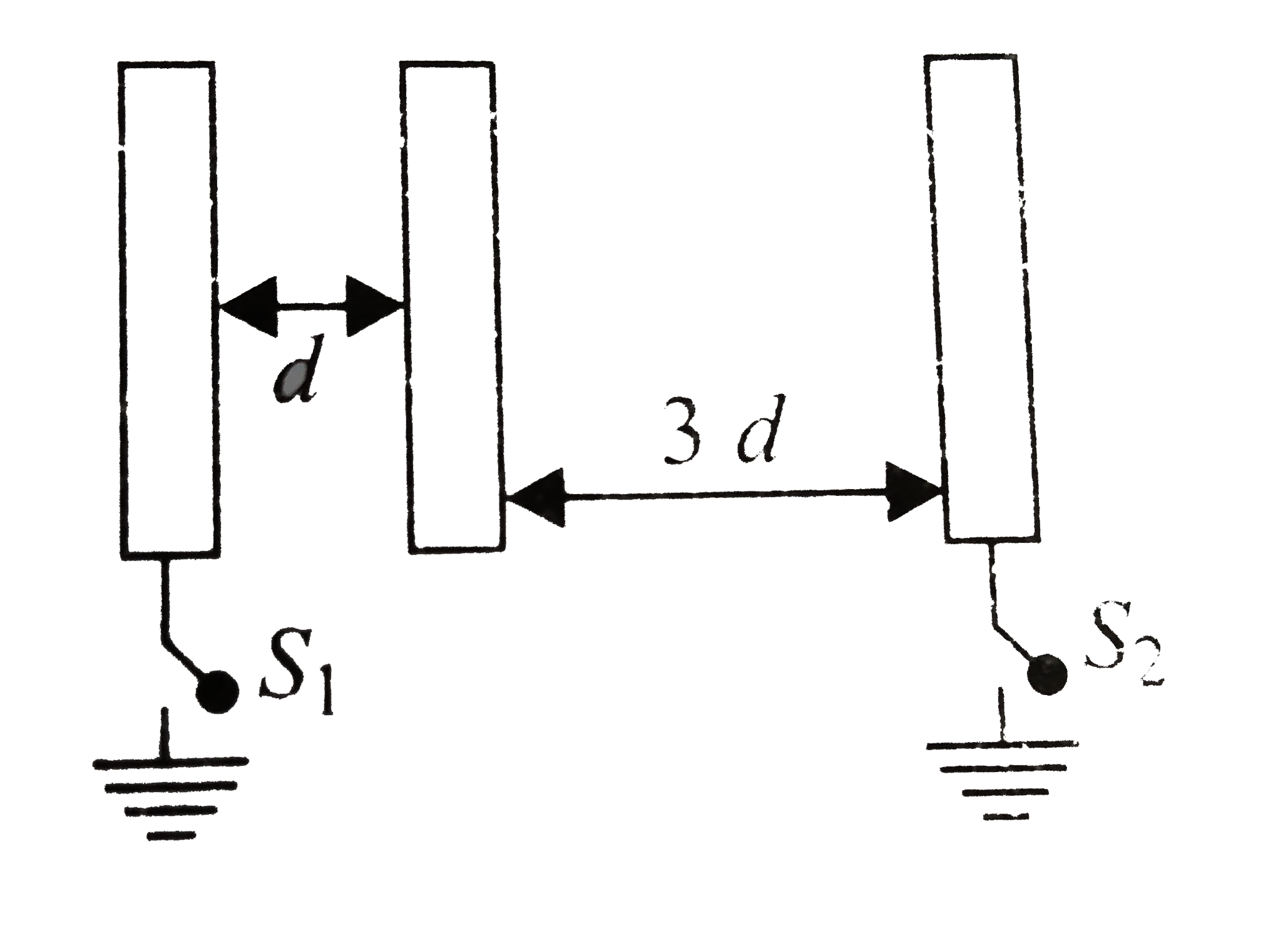
The charge that will flow to the earth when only switch `S_1` is connected to the earth is
View SolutionThree metallic plates out of which the middle is given charge Q as shown in the figure. The outer plates can be earthed with the help of switches `S_1 and S_2` . The area of each plates is the same. Answer the following question based on the given passage.
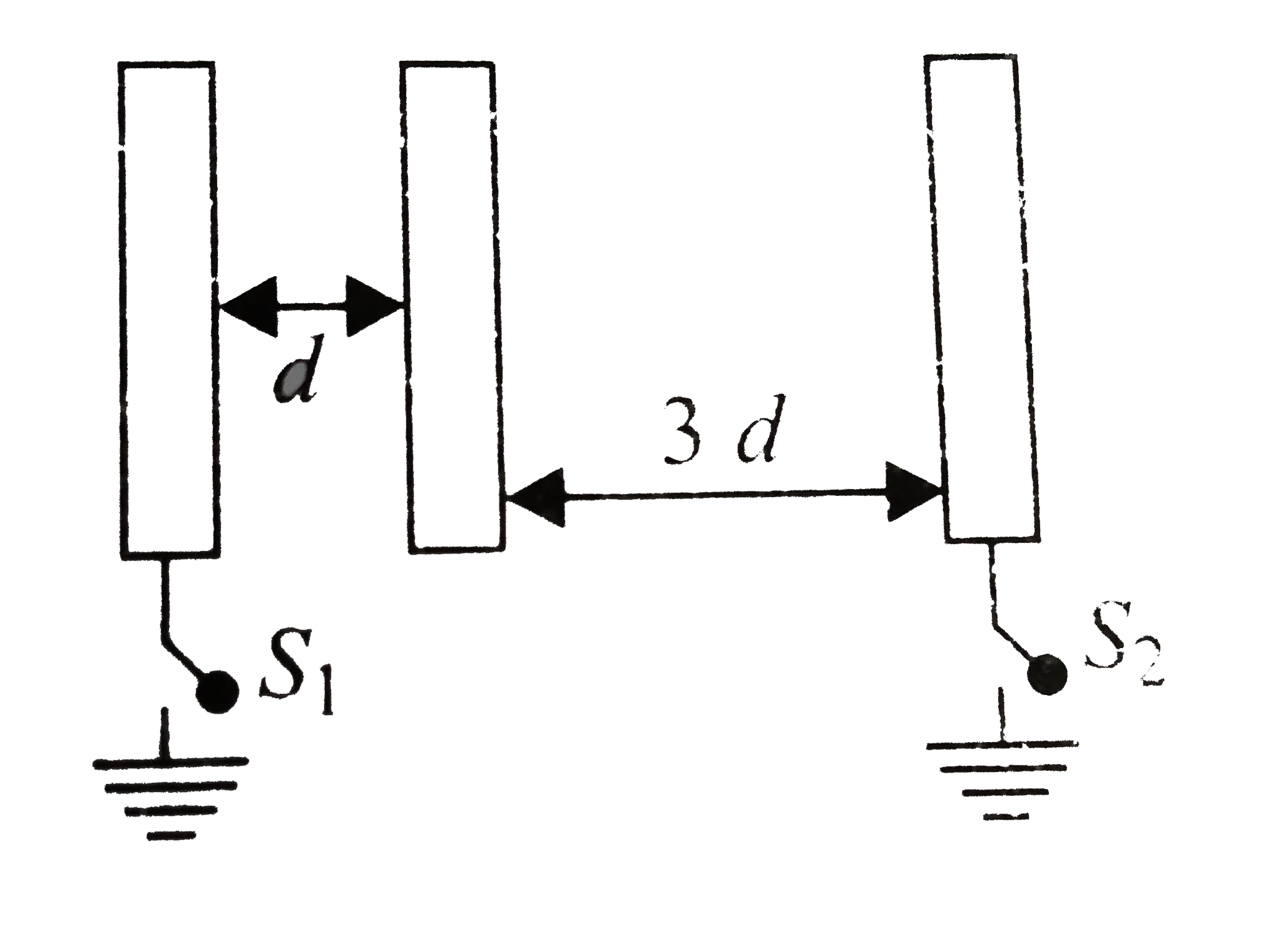
The charge that will flow to the earth through `S_2` when both switches `S_1 and S_2` are grounded simultaneously is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
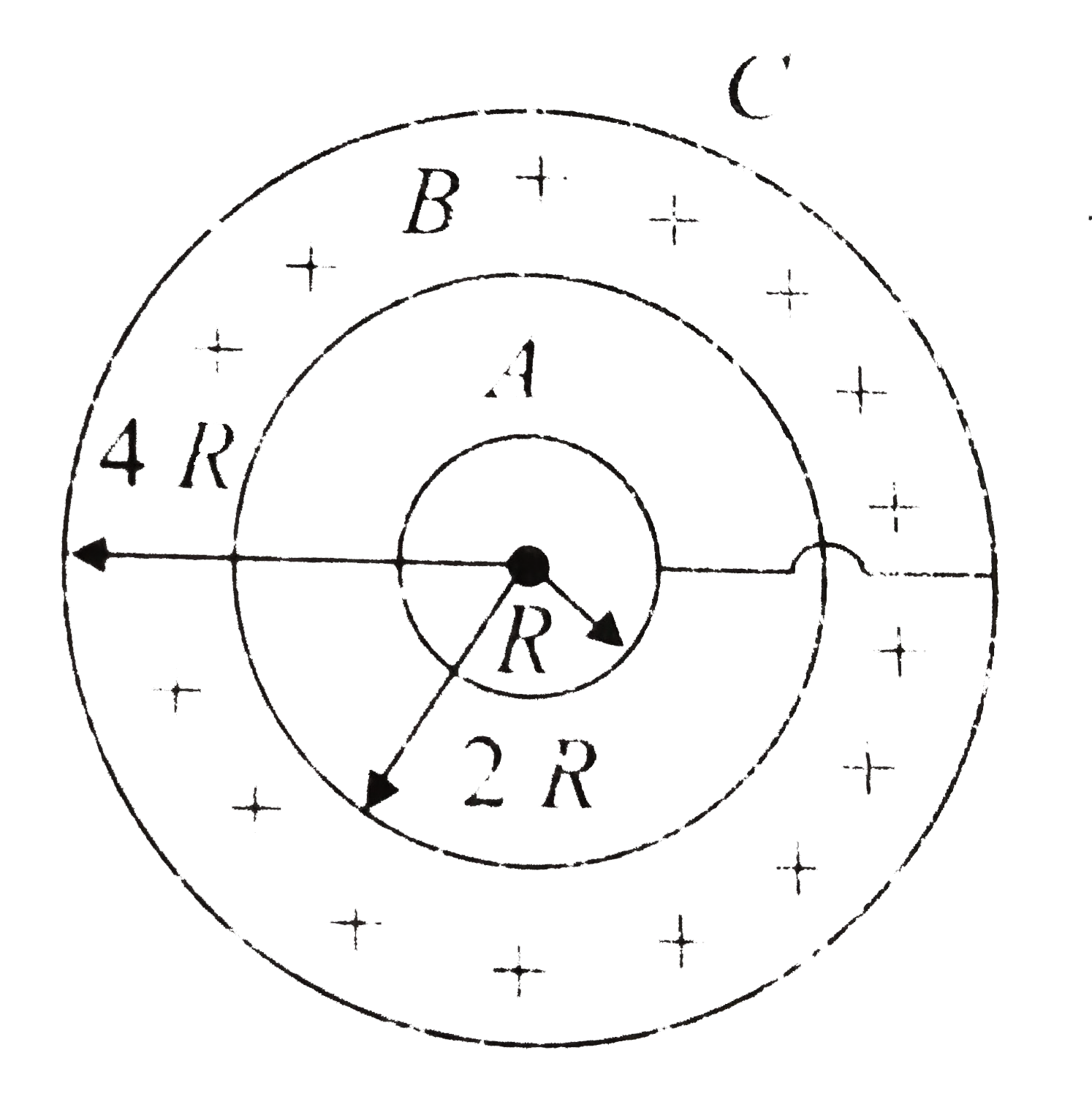
Charge on conductor A is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
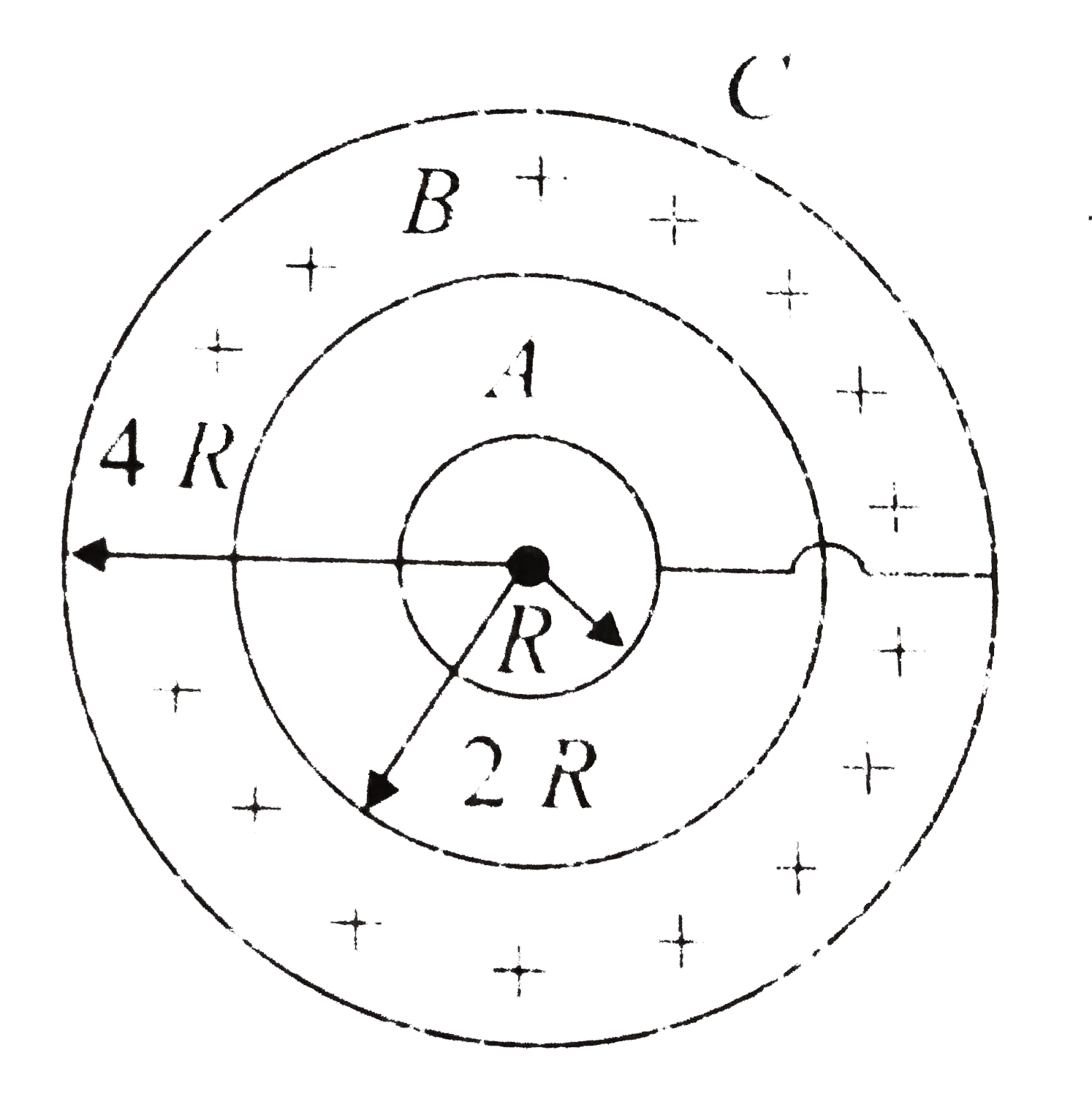
Potential at A is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
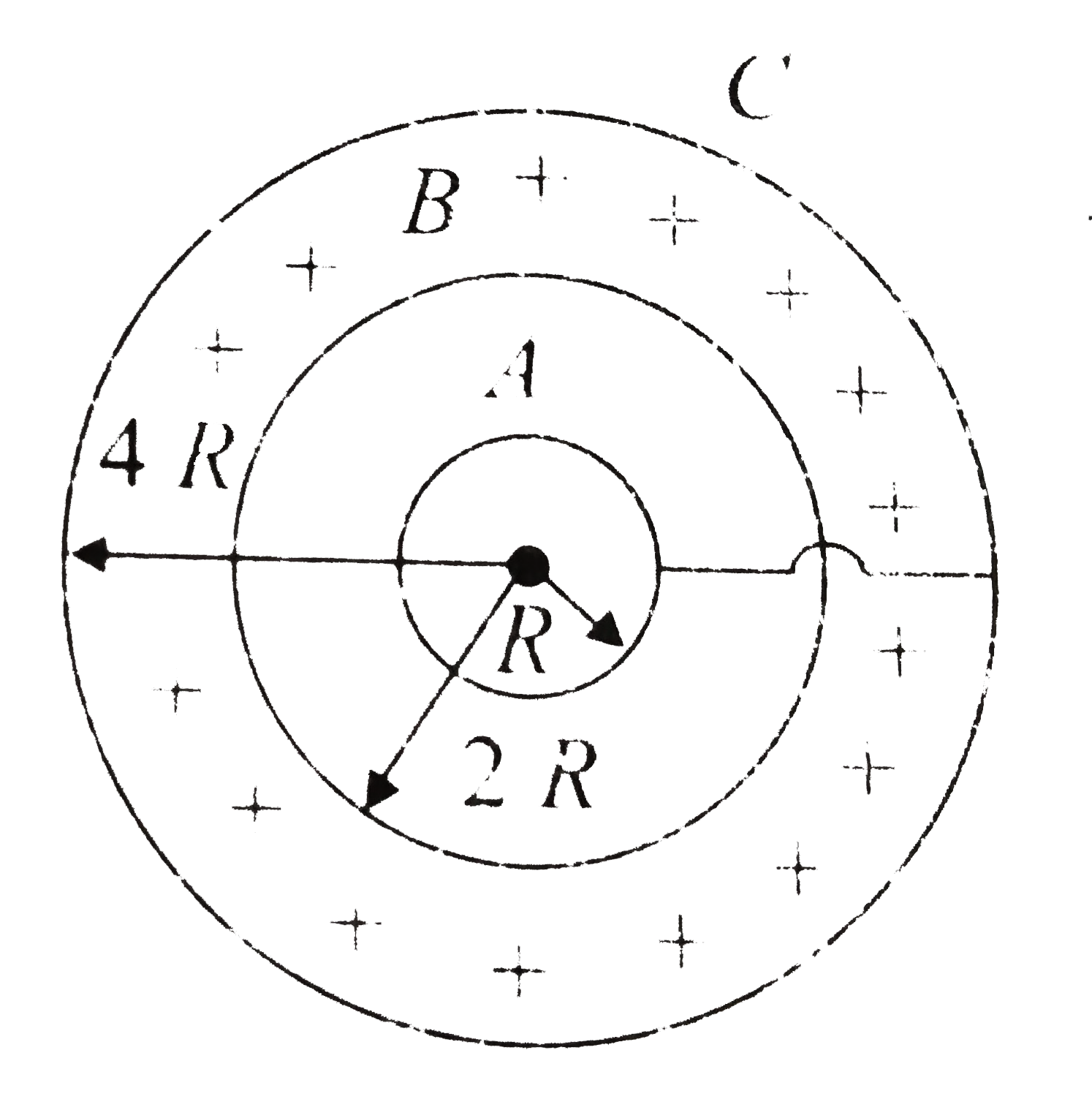
Potential at B is
View SolutionTwo capacitros of capacity `6 mu F` are charged to 100 V and 50 V separately and connected as shown. Now all the three switches `S_(1), S_(2)` and `S_(3)` are closed.
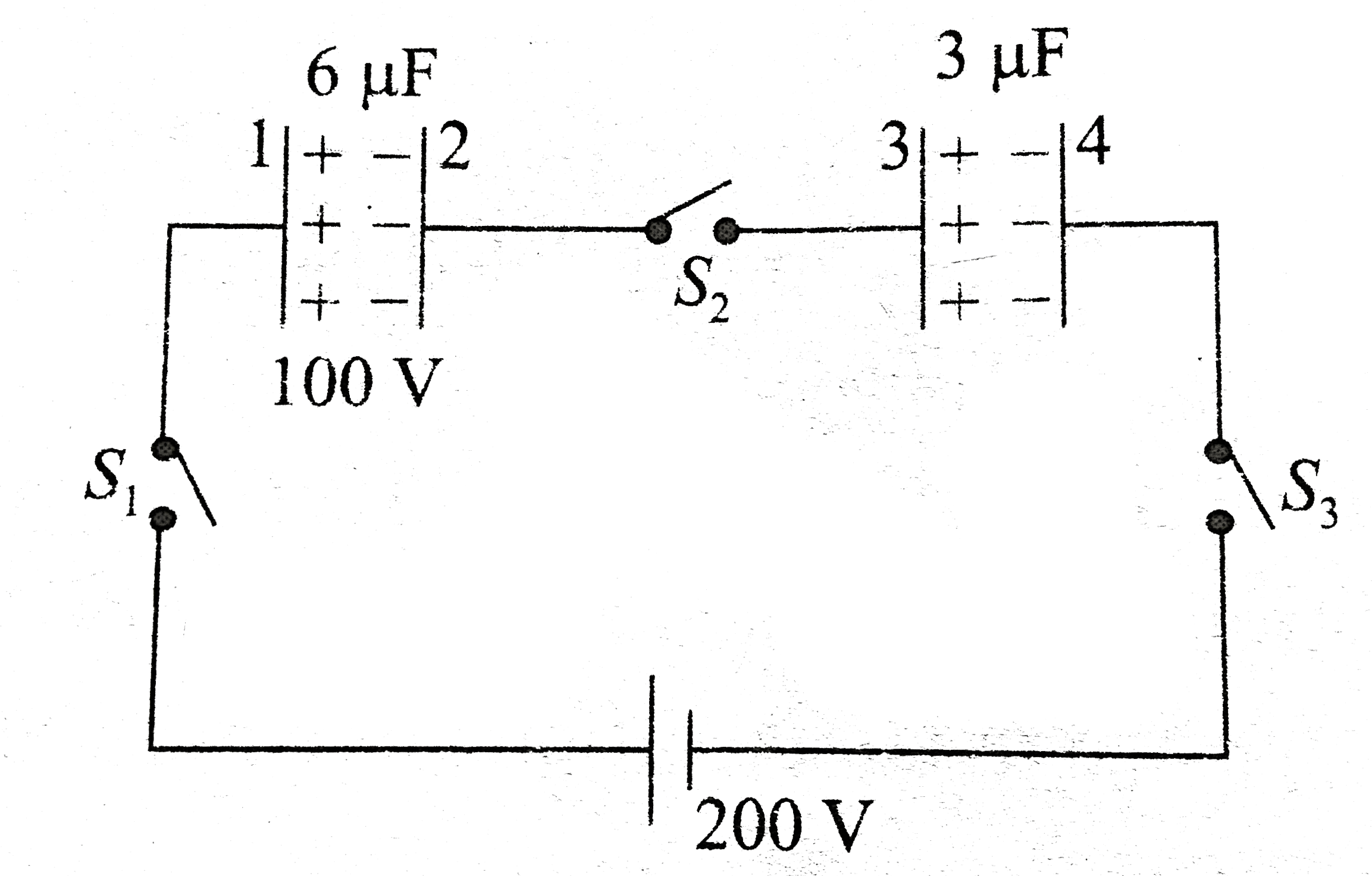
Suppose `q_(1), q_(2)` and `q_(3)` be the magnitudes of charge flown from switches `S_(1), S_(2)` and `S_(3)` after they closed. Then
View SolutionTwo capacitors of capacity `6 muF` and `3 muF` are charge `100 V` and `50 V` separately and connected as shown in figure. Now all the three switches `S_(1),S_(2)`, and `S_(3)` are closed.
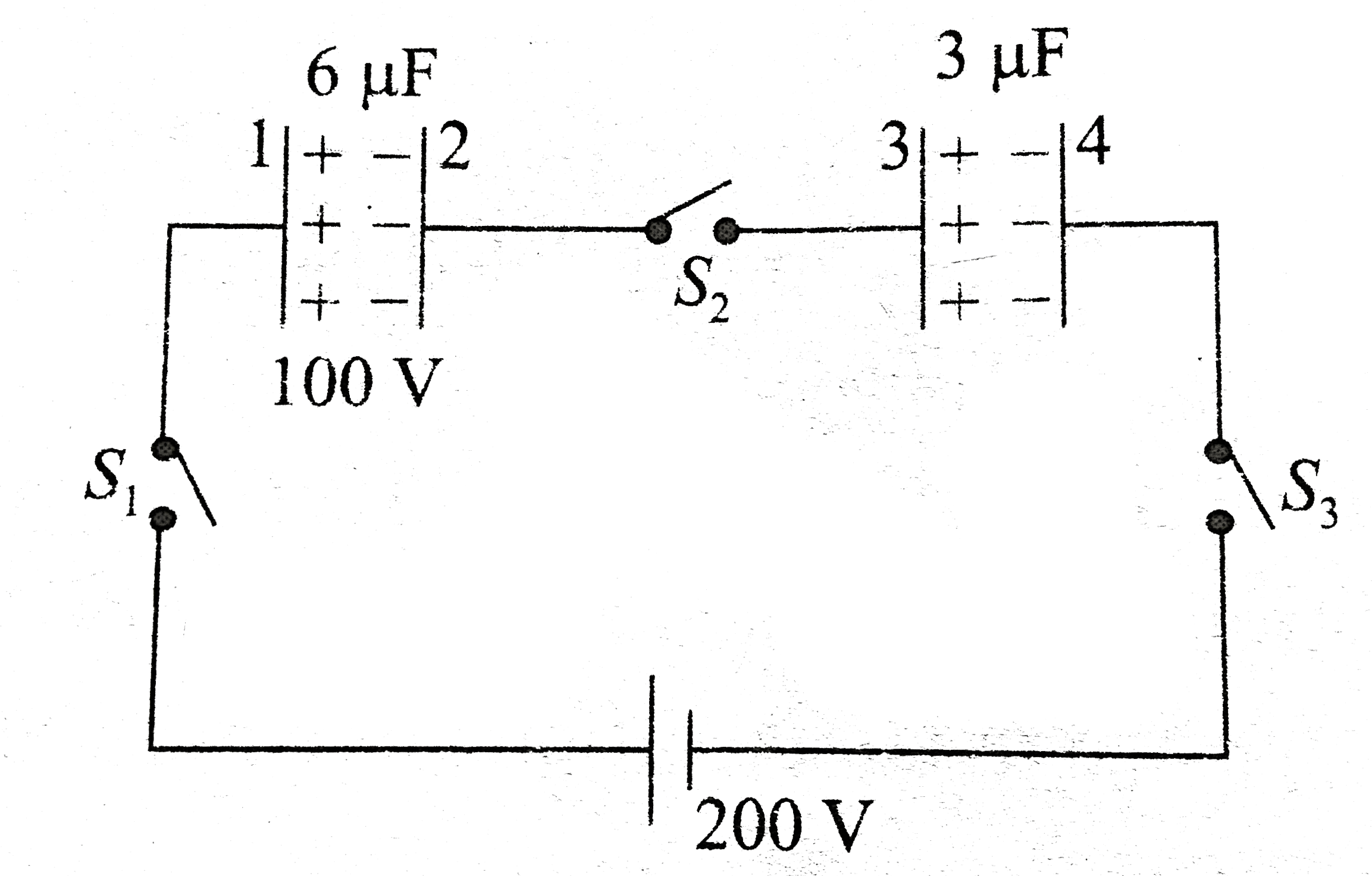
Charge on the `3 muF` capacitor in steady state willl be.
View SolutionTwo capacitros of capacity `6 mu F` are charged to 100 V and 50 V separately and connected as shown. Now all the three switches `S_(1), S_(2)` and `S_(3)` are closed.
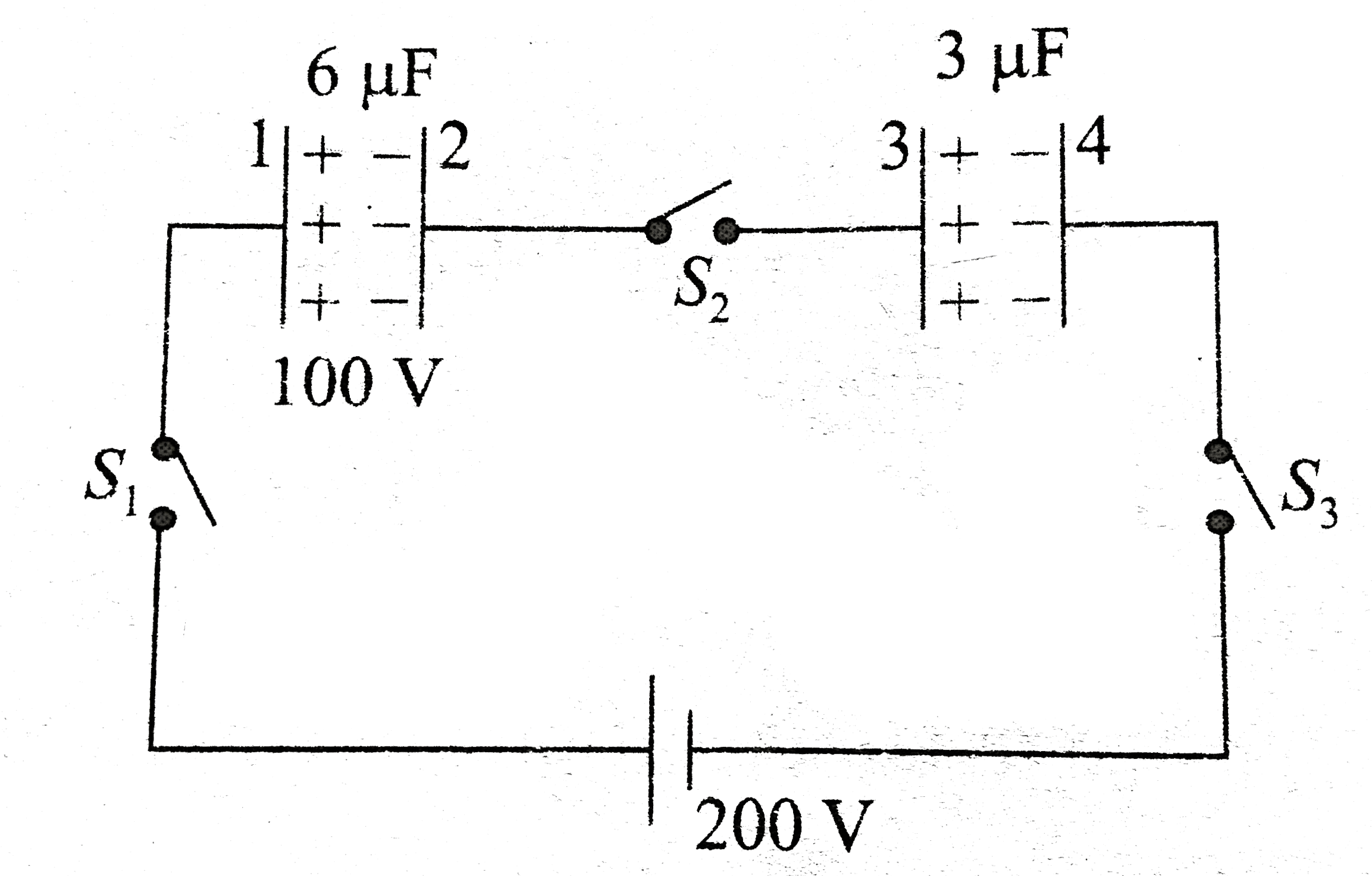
Suppose `q_(1), q_(2)` and `q_(3)` be the magnitudes of charge flown from switches `S_(1), S_(2)` and `S_(3)` after they closed. Then
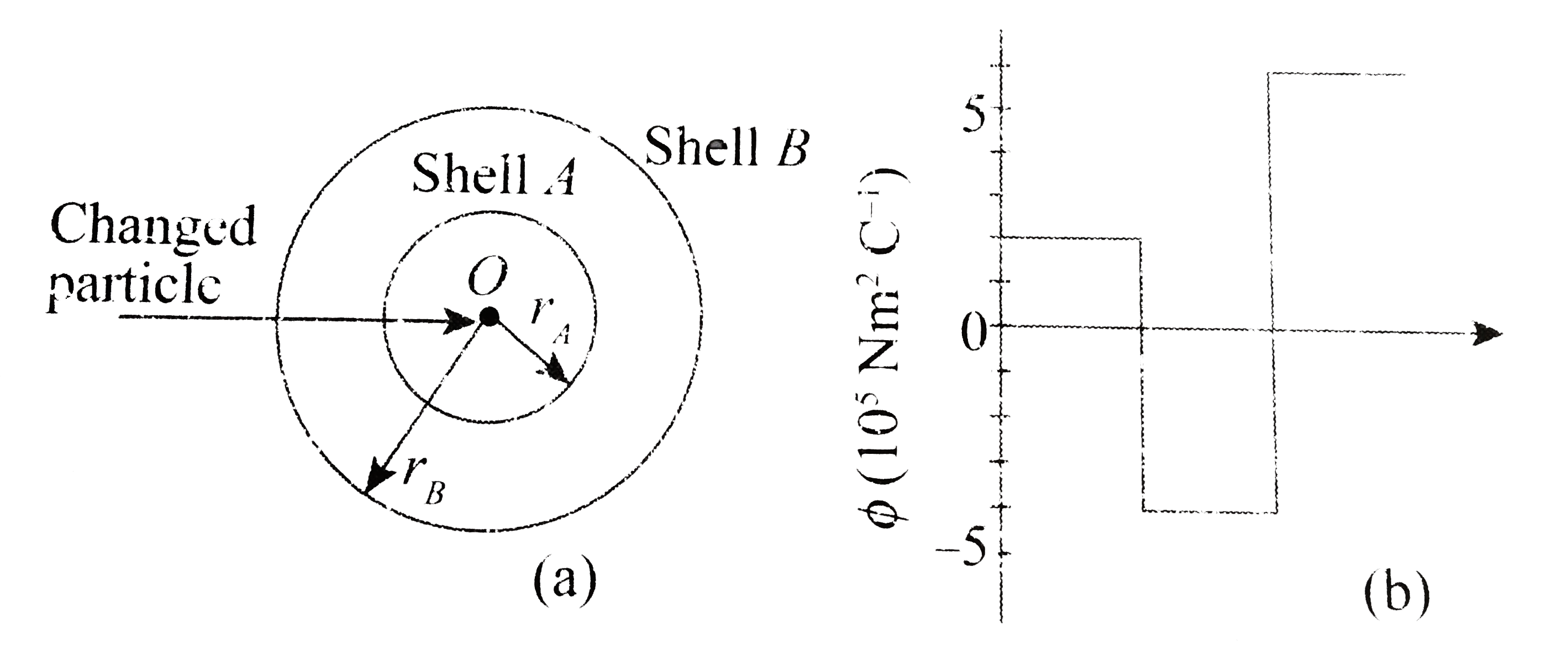
View SolutionA charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux `phi` through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
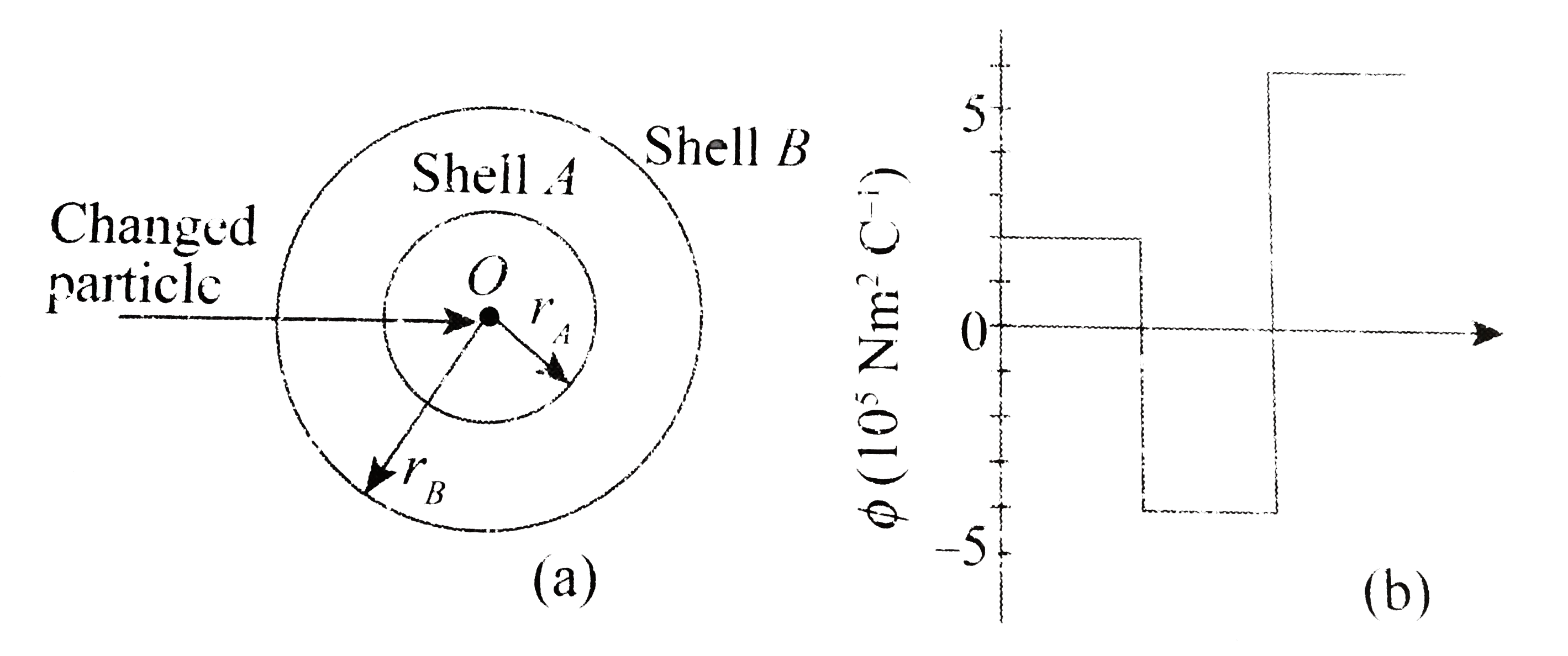 ,
,
What is the charge on the central particle?
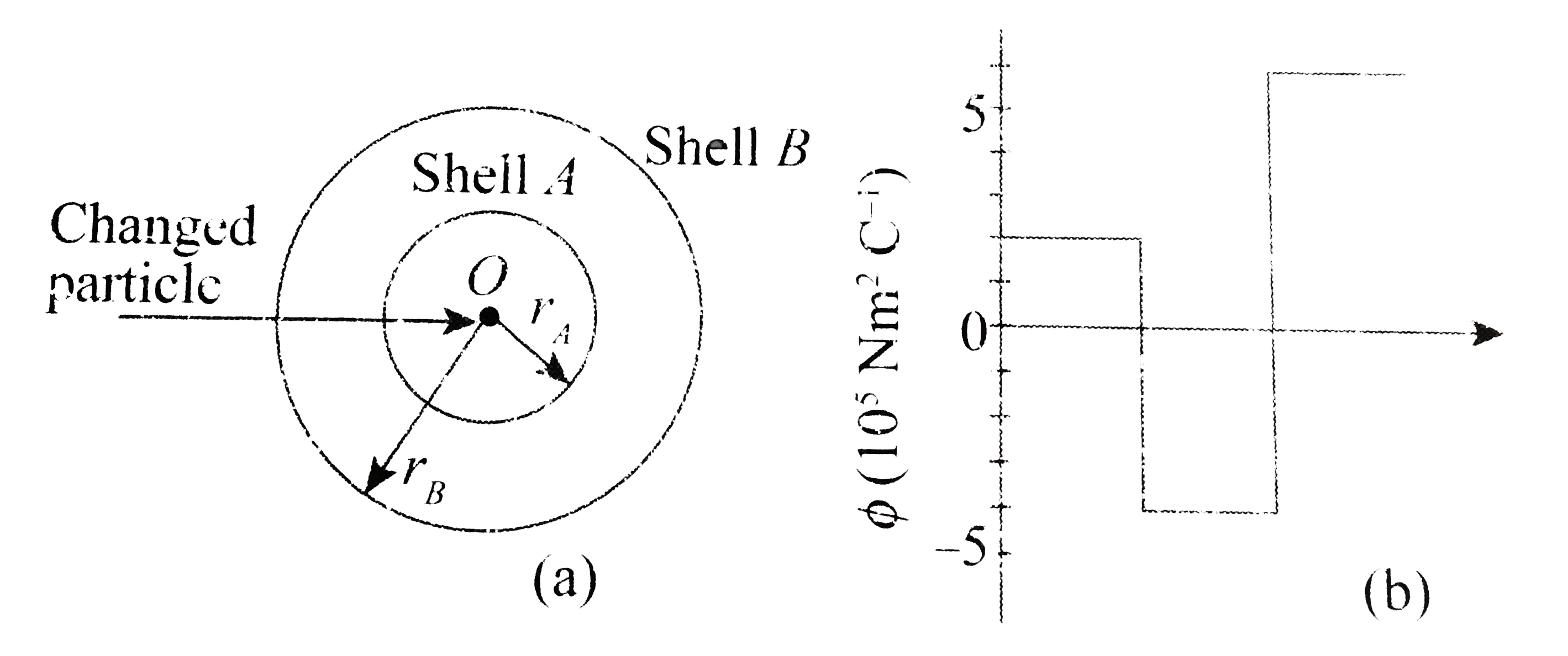
View SolutionA charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux `phi` through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
 ,
,
What is the charge on shell A?
View SolutionA charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux `phi` through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
 ,
,
In which range of the values of r is the electric field zero?
View SolutionCapacitor `C_(3)` in the circuit is a veriable capacitor (its capacitance can be varied). Group is plotted between potential difference `V_(1)` (across capacitor `C_(1)`) versus `C_(3)`. Electric potential `V_(1)` approaches to 10 V as `C_(3) rarr oo`. Given that `C_(1) + C_(2) = 10 mu F`

EMF of the battery is equal to
View SolutionCapacitor `C_(3)` in the circuit is a variable capacitor (its capacitance can be varied). Graph is plotted between potential difference `V_(1)` (across capacitor `C_(1)`) versus `C_(3)`. Electric potential `V_(1)` approaches to 10 V as `C_(3) rarr oo`. Given that `C_(1) + C_(2) = 10 mu F`

The capacitance of the capacitor `C_(1)` value
View SolutionCapacitor `C_(3)` in the circuit is a variable capacitor (its capacitance can be varied). Graph is plotted between potential difference `V_(1)` (across capacitor `C_(1)`) versus `C_(3)`. Electric potential `V_(1)` approaches to 10 V as `C_(3) rarr oo`. Given that `C_(1) + C_(2) = 10 mu F`

The capacitance of the capacitor `C_(1)` value
View SolutionIn a region , an electroc field `E = 10NC^(-1)` making an angle of `theta = 30^@` with the horizontal plane is present. Coefficient of restitution between ball and surface is `e = 0.2.` Ball has charge `q = -2C` over it and mass m = 2 kg . Ball is projected at an angle of `theta = 30^@` with the horizontal with speed `u = 10ms^(-1)`
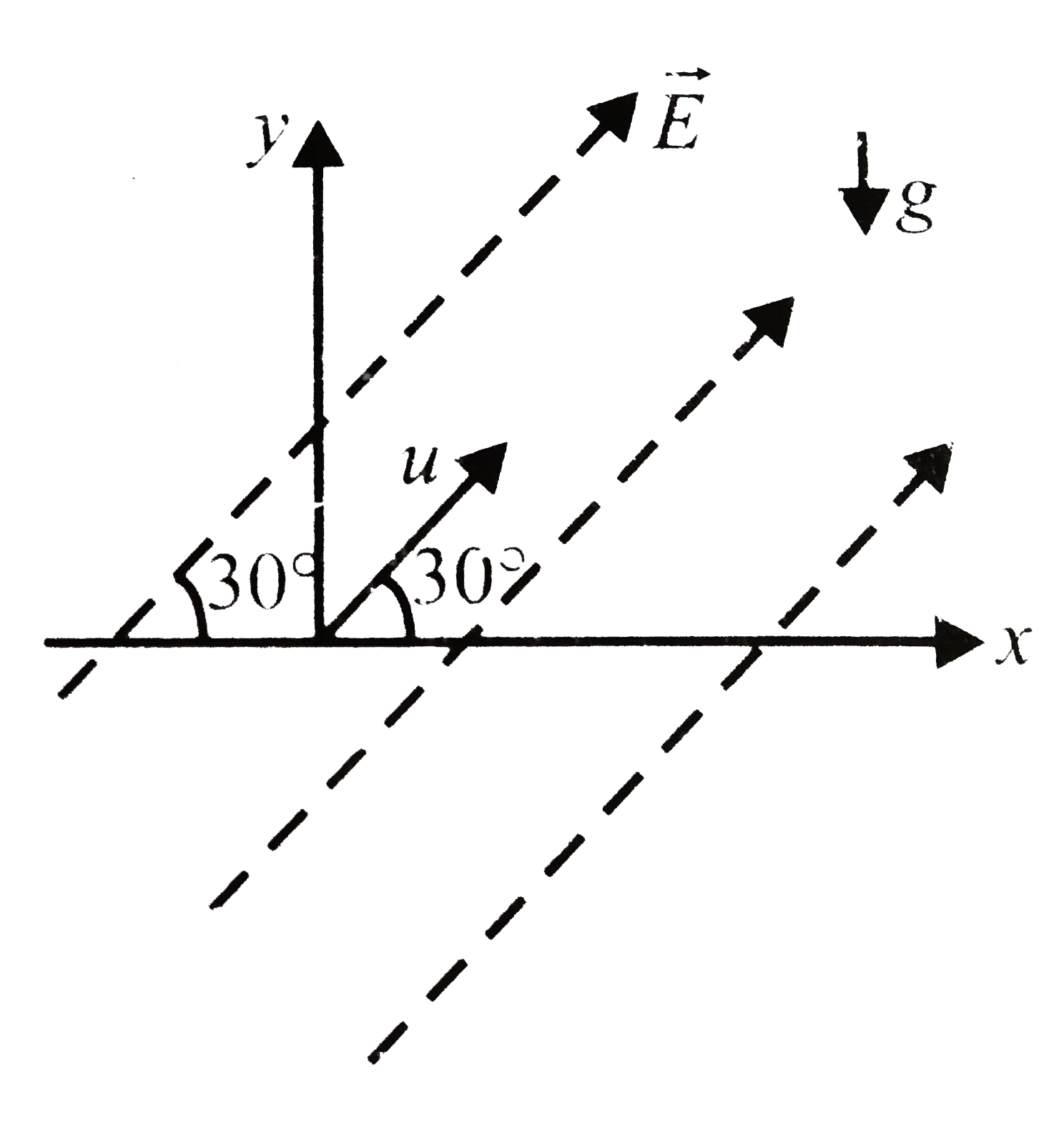
Horizontal distance traveled up to first rebound is
View SolutionIn a region , an electroc field `E = 10NC^(-1)` making an angle of `theta = 30^@` with the horizontal plane is present. Coefficient of restitution between ball and surface is `e = 0.2.` Ball has charge `q = -2C` over it and mass m = 2 kg . Ball is projected at an angle of `theta = 30^@` with the horizontal with speed `u = 10ms^(-1)`
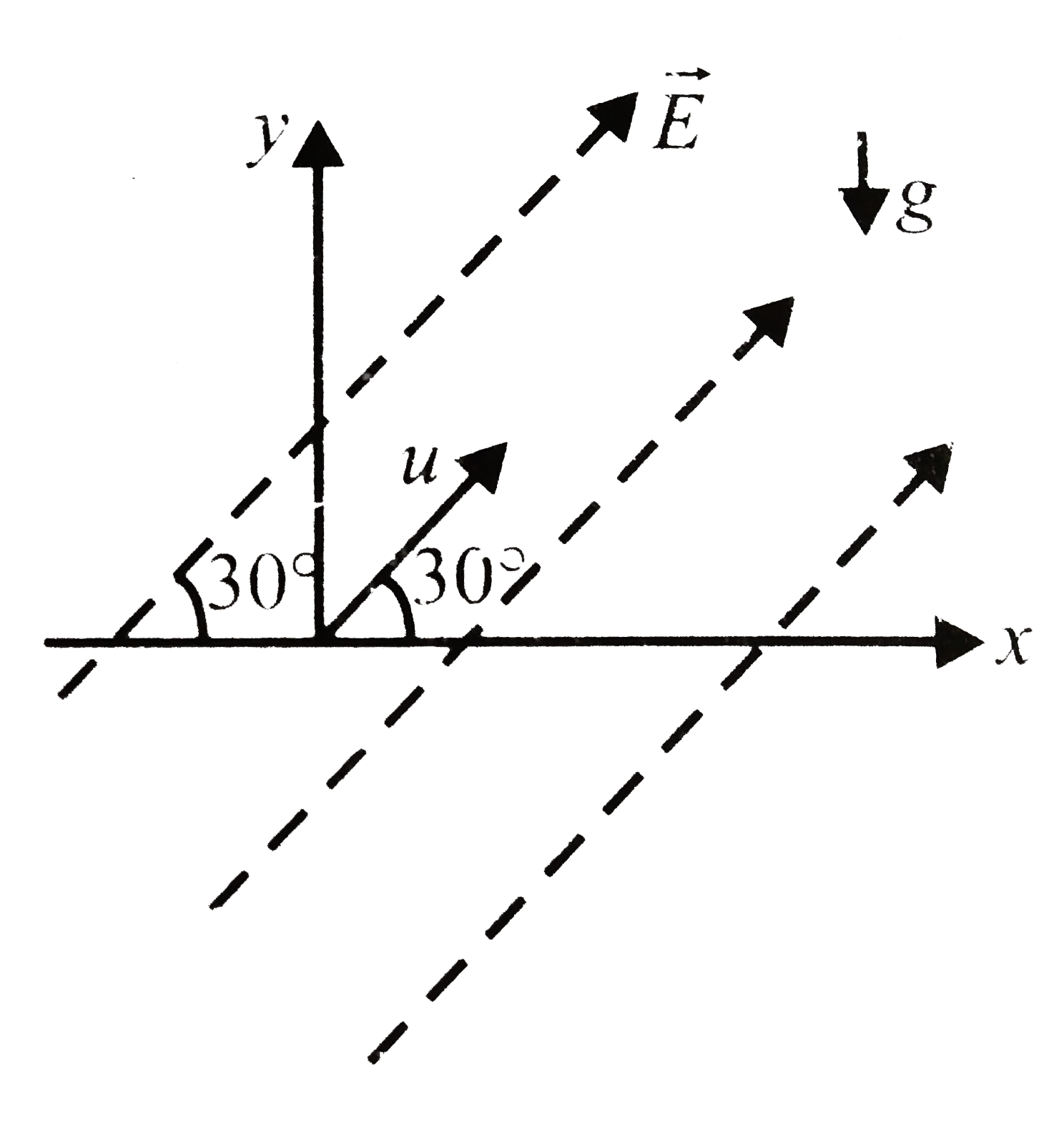
After first impact with the ground,
View SolutionTwo circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field `E = 10^(5) NC^(-1)` directed vertically upward as shown in figure. Distance between centers of the rings A and B `(C_A and C_B)is 40 cm`. Ring A has positive charge `q_A = 10muC` and B has a negative charge `q_B = -20muC`. A particle of mass m and charge `q = 10muC` is released from rest at the center of ring A. If particle moves along `C_AC_B,` then

Work done by electric field, when particle moves from `C_A to C_B` is
View SolutionTwo circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field `E = 10^(5) NC^(-1)` directed vertically upward as shown in figure. Distance between centers of the rings A and B `(C_A and C_B)is 40 cm`. Ring A has positive charge `q_A = 10muC` and B has a negative charge `q_B = -20muC`. A particle of mass m and charge `q = 10muC` is released from rest at the center of ring A. If particle moves along `C_AC_B,` then
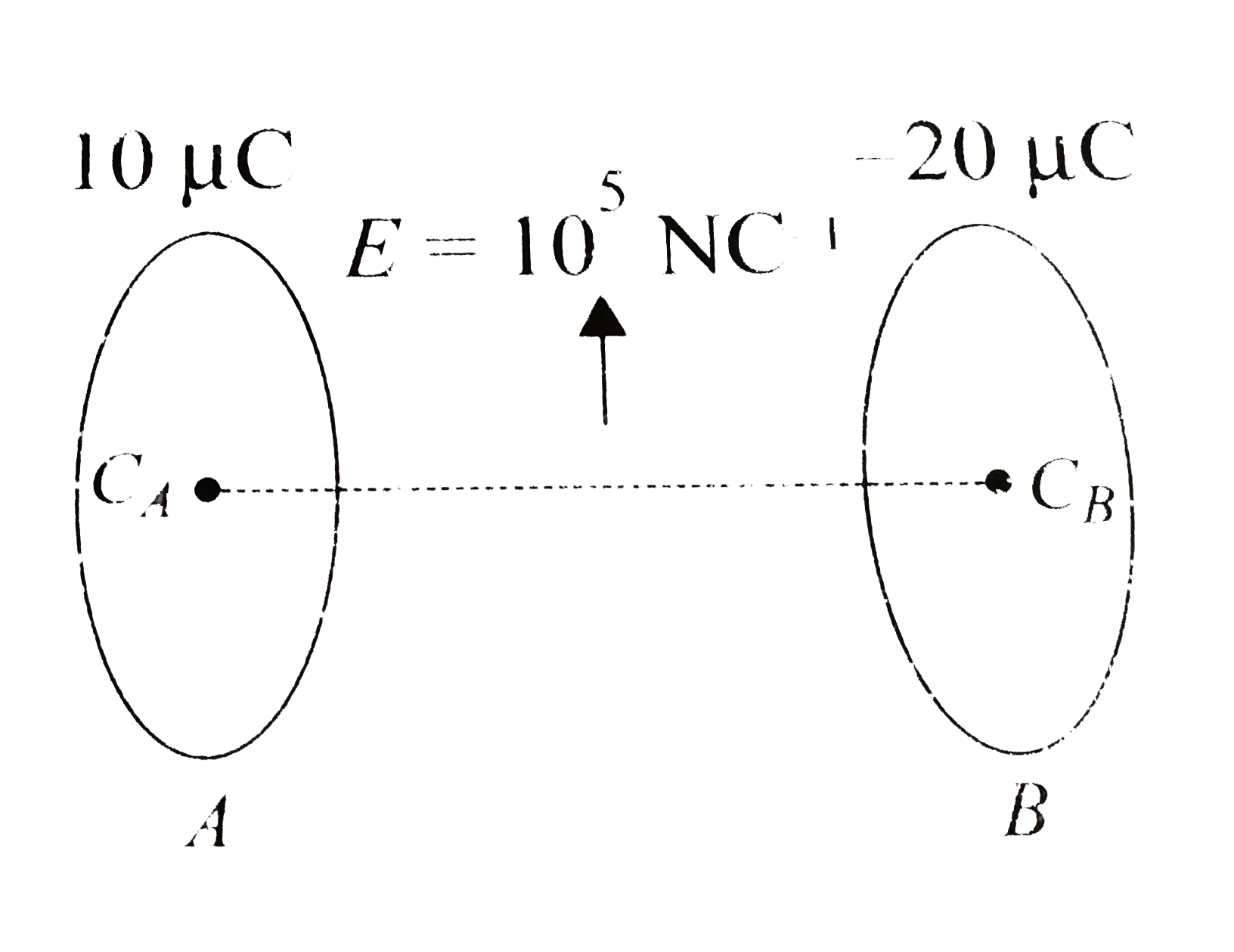
Speed of particle when it reaches at center of B is
View SolutionFigure shows four plates each of plate area A and separated between plates is d. Two switches `S_(w_1) and S_(w_2)` can activate two batteries in the circuit.
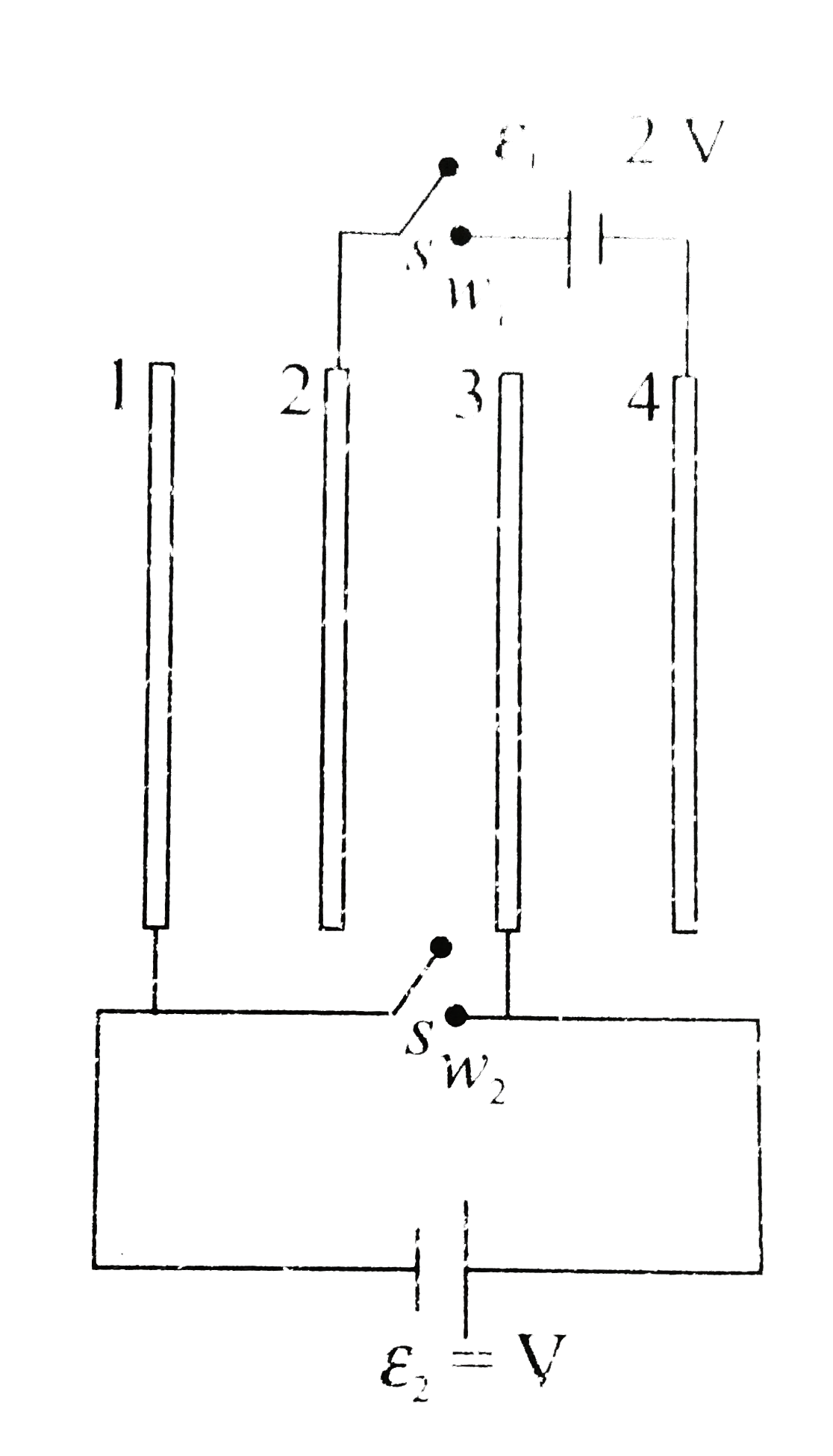
Switch `S_(w_1) and S_(w_2)` are closed, What is the charge on plate 2?
View SolutionFigure shows four plates each of plate area A and separated between plates is d. Two switches `S_(w1) and S_(w_2)` can activate two batteries in the circuit.

What is the charge passing through battery 1?
View SolutionFigure shows four plates each of plate area A and separated between plates is d. Two switches `S_(w_1) and S_(w_2)` can activate two batteries in the circuit.

Switch `S_(w_1) and S_(w_2)` are closed, What is the charge on plate 2?
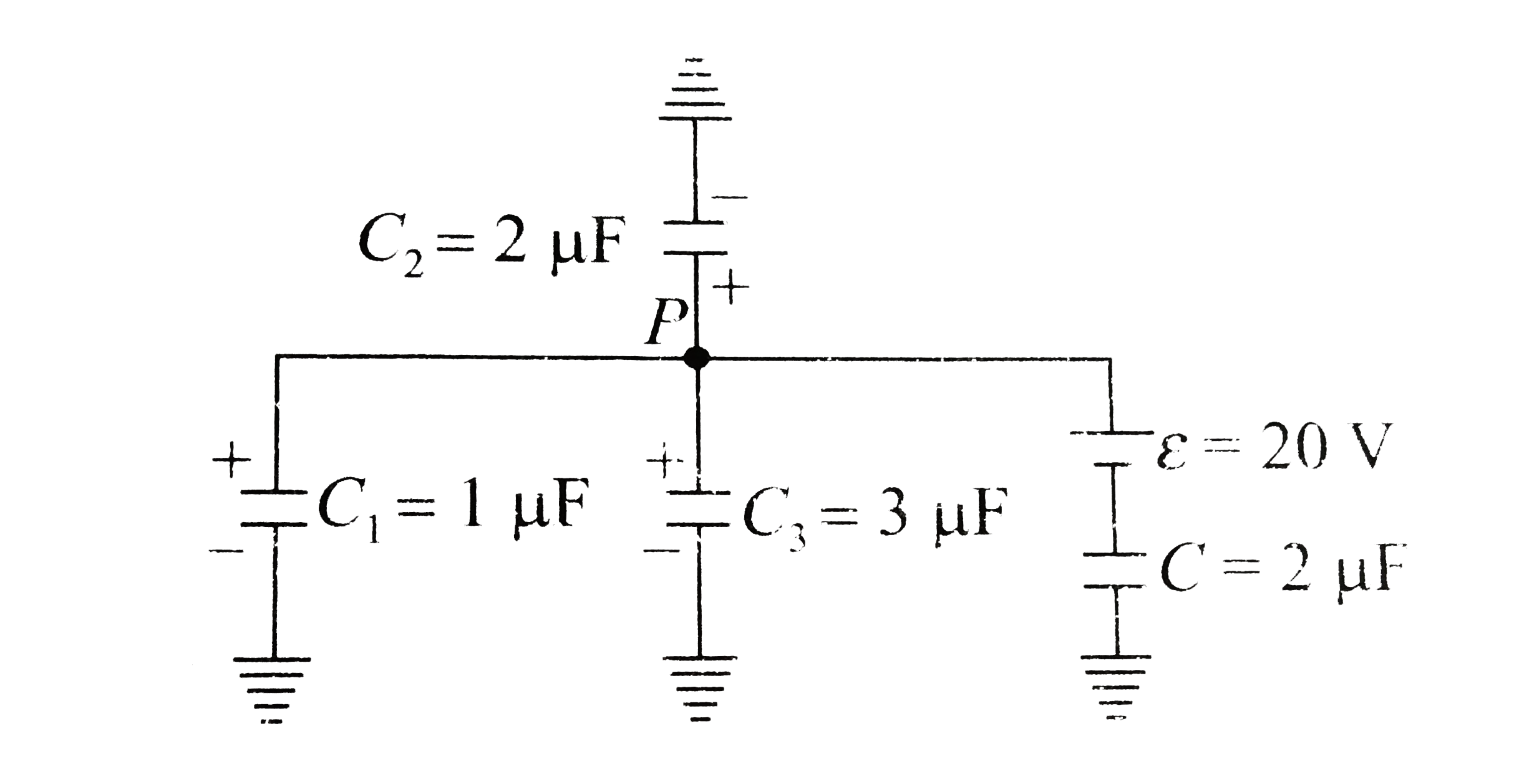
View SolutionThree capacitors `C_1,C_2,andC_3` of capacitance `1muF, 2muF, and 3muF`, respectively, are charged separately as shown in the figure. Now these charged capacitors are connected to a battery of `epsilon = 20 V` and an uncharged capacitor of `C = 2muF` as shown in figure.
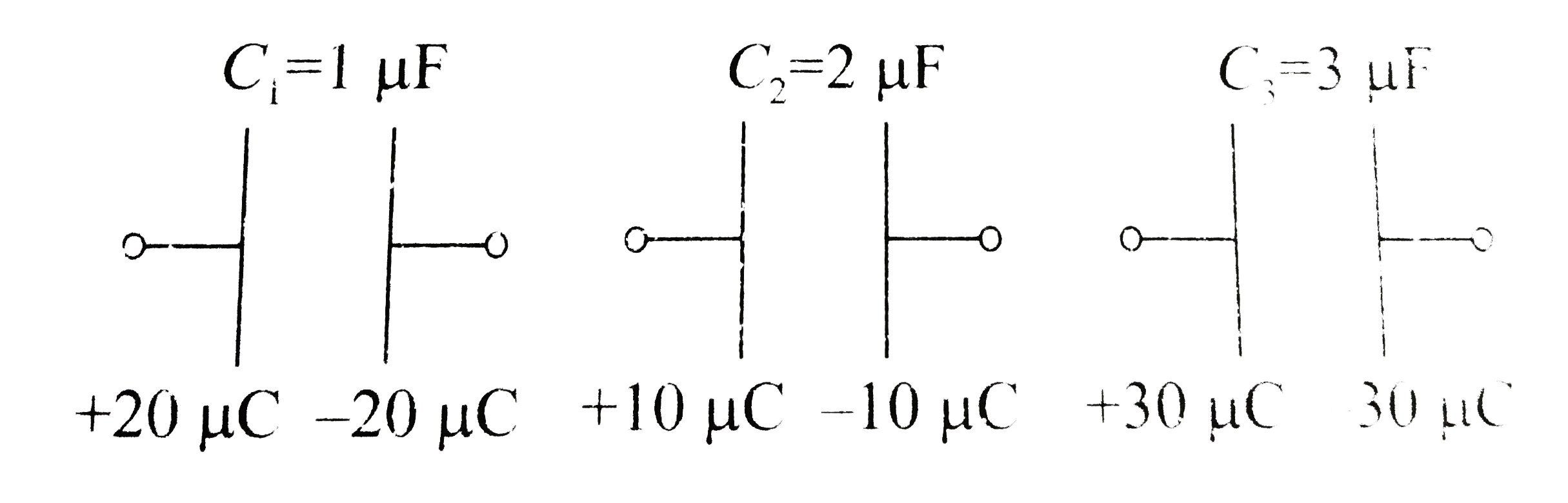 ,
, 
The charge on capacitor marked C is
View SolutionThree capacitors `C_1,C_2,andC_3` of capacitance `1muF, 2muF, and 3muF`, respectively, are charged separately as shown in the figure. Now these charged capacitors are connected to a battery of `epsilon = 20 V` and an uncharged capacitor of `C = 2muF` as shown in figure.
 ,
, 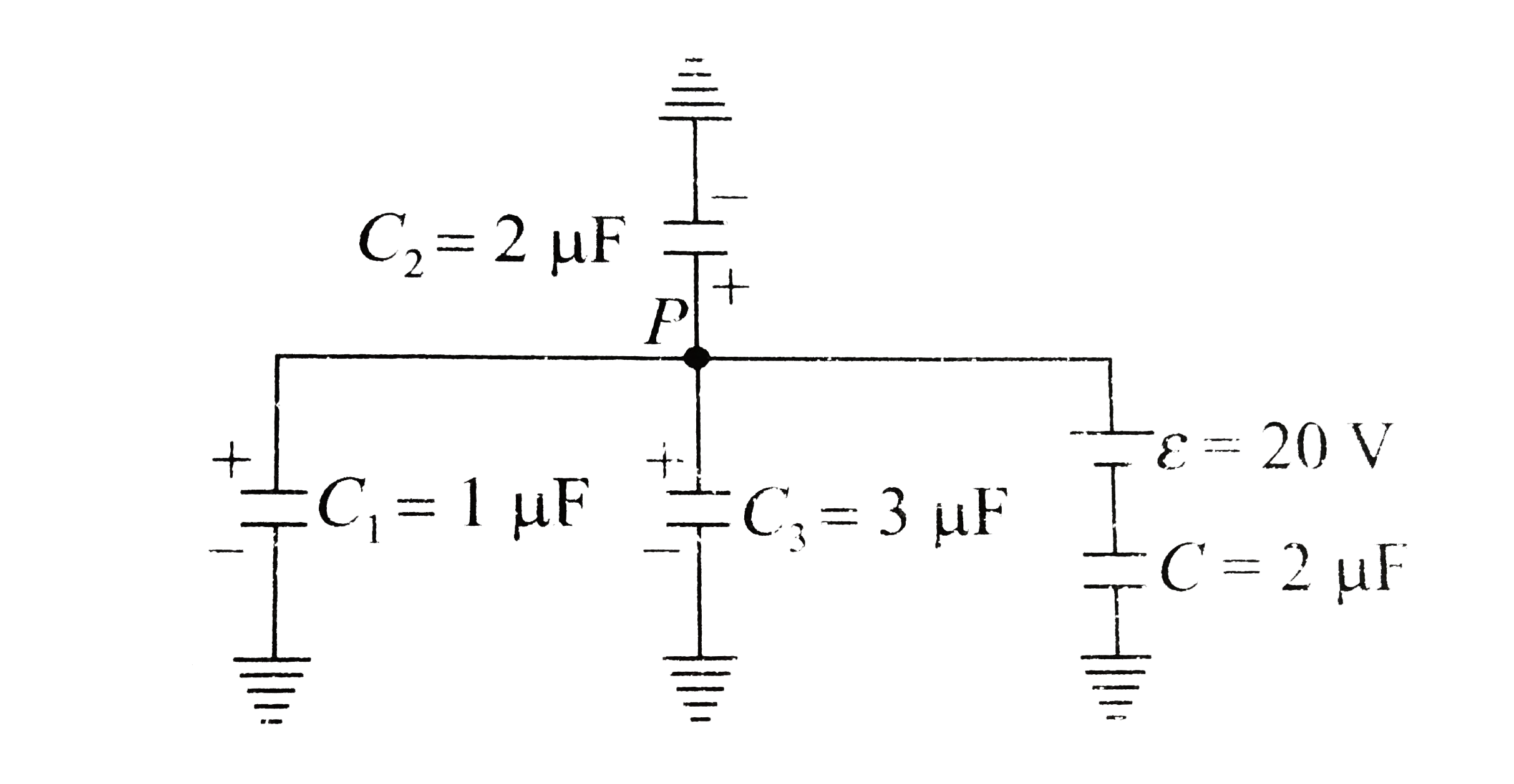
The potential of point P is
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, `q = 1muC` , mass of each particle `m=6g`. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

What is the tension in the string?
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, `q = 1muC` , mass of each particle `m=6g`. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

Now suppose a third charge of equal value `+q` is fixed at the point `(a//2,0)` and the system of charges A and B is released. There is no friction between third charge and string. Find the maximum velocity of the system of charges A and B.
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, `q = 1muC` , mass of each particle `m=6g`. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

What is the tension in the string?
View SolutionTwo nonconducting plates A and B of radii 2R and 4R, respectively, are kept at distance x and 2x from the point charge q. A surface cutout of a nonconducting shell A is kept such that is center coincides with the point charge. Each plate and spherical surface carries surface charge density `sigma`.
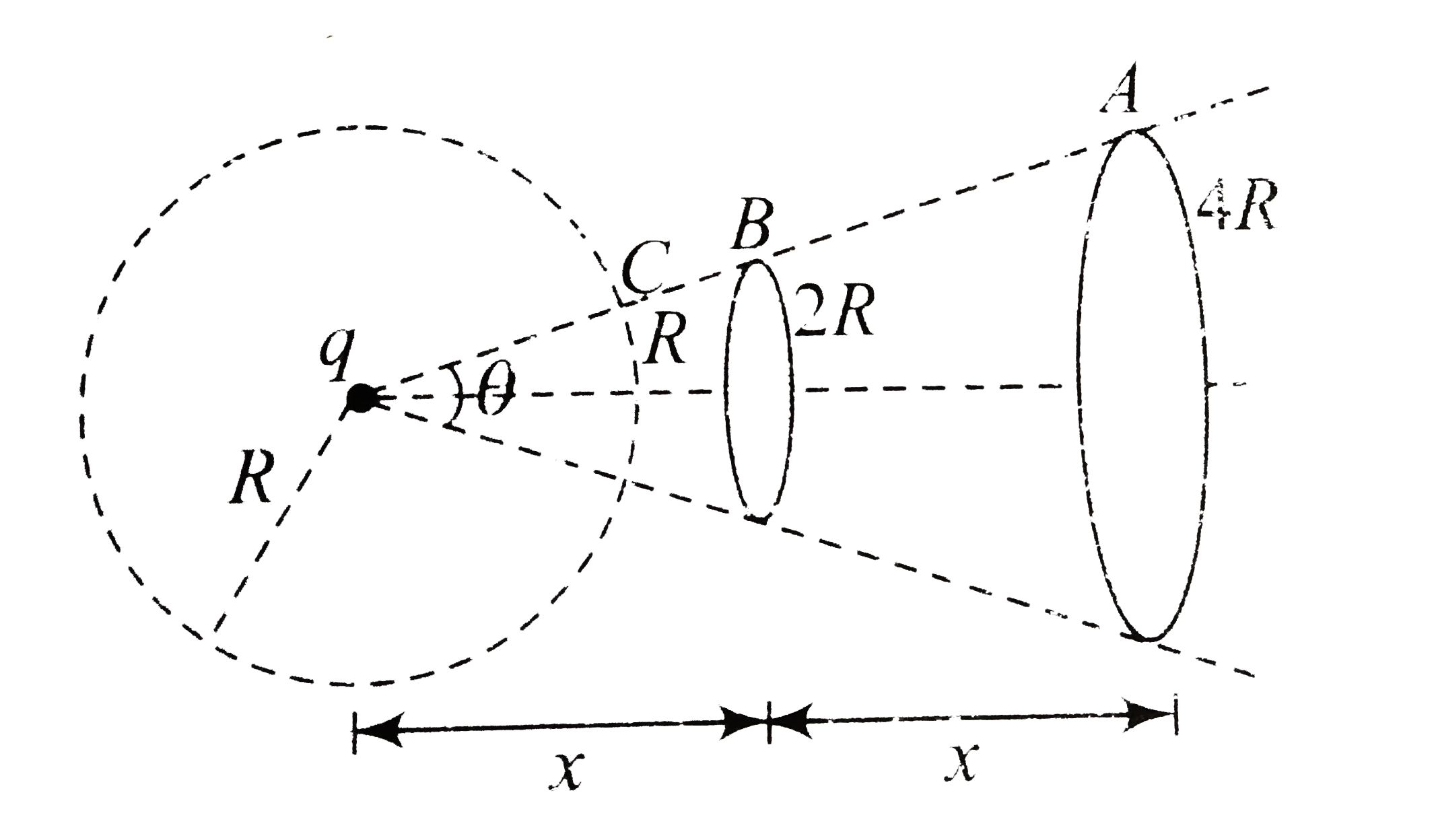
If `F_A,F_B,and F_C` are the forces on plate A, plate B, and spherical surface C due to charge q, respectively, then
View SolutionTwo nonconducting plates A and B of radii 2R and 4R, respectively, are kept at distance x and 2x from the point charge q. A surface cutout of a nonconducting shell A is kept such that is center coincides with the point charge. Each plate and spherical surface carries surface charge density `sigma`.
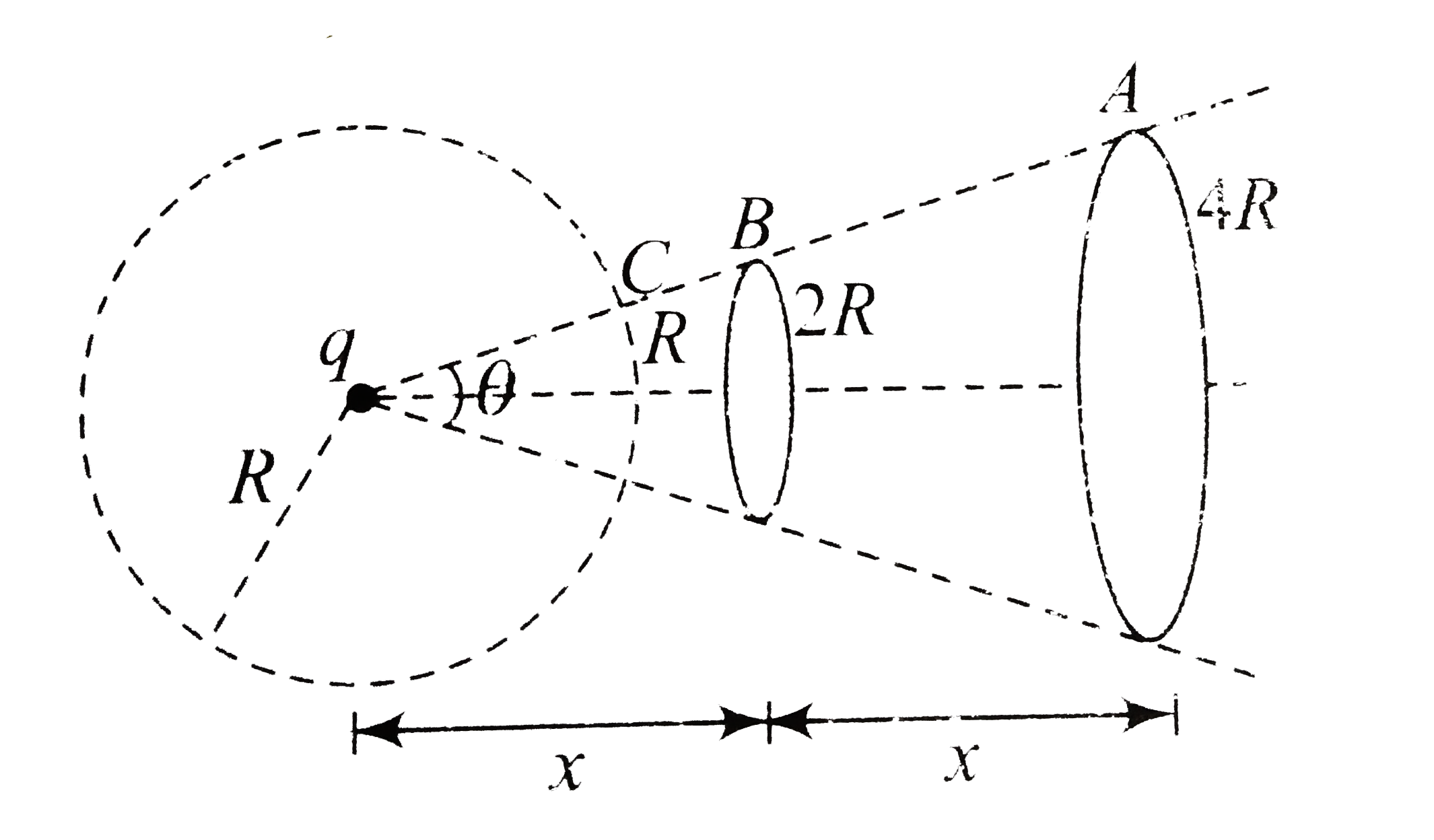
If `phi_1` is flux through surface of (B) due to electric field to (A) and `phi_2` is the flux through (A) due to electric field of (B), then
View SolutionTwo nonconducting plates A and B of radii 2R and 4R, respectively, are kept at distance x and 2x from the point charge q. A surface cutout of a nonconducting shell A is kept such that is center coincides with the point charge. Each plate and spherical surface carries surface charge density `sigma`.
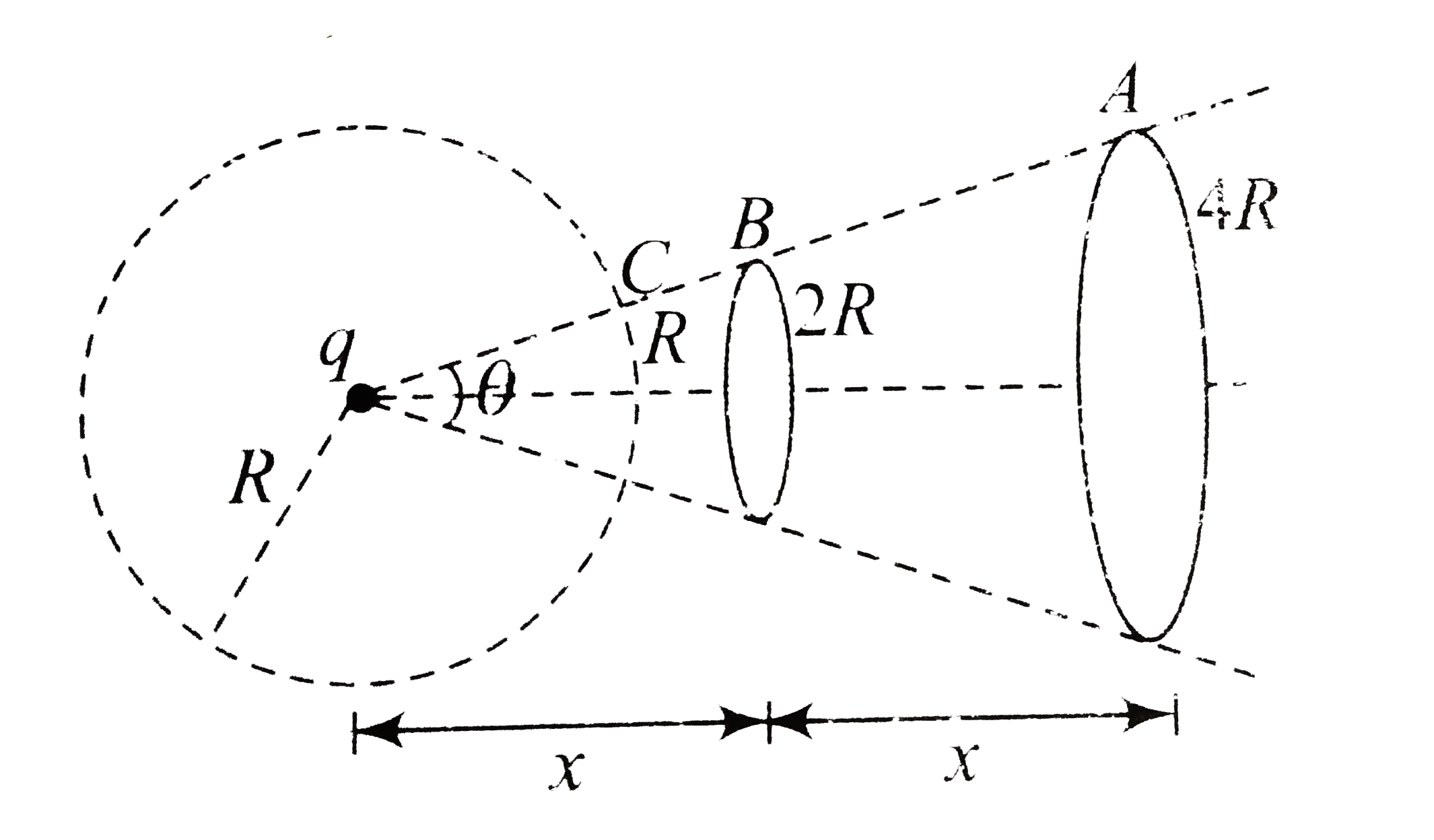
If distance x and radius R are doubled so that `F_A` becomes `F'_A` and `F_B` becomes `F'_B`, then the correct option is
View SolutionTwo very large parallel disks of charge have their centers on the x-axis and their planes perpendicular to the x-axis. The disk that intersects x = -R has uniform positive surface charge density `+sigma`, the disk that intersects `x = +R` has uniform negative surface charge density `-sigma`. (i)
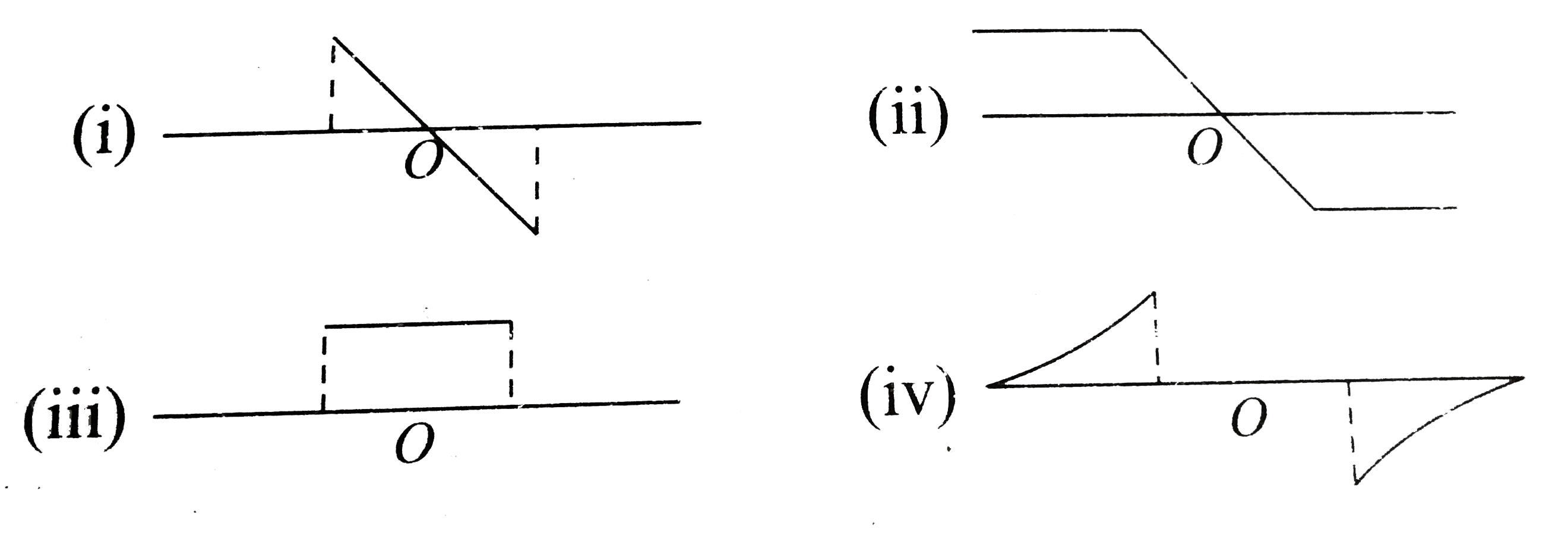 ,
,
Which graph best represents the plot of the x-component of the electric field vector on the x-axis?
View SolutionTwo very large parallel disks of charge have their centers on the x-axis and their planes perpendicular to the x-axis. The disk that intersects x = -R has uniform positive surface charge density `+sigma`, the disk that intersects `x = +R` has uniform negative surface charge density `-sigma`. `(i)
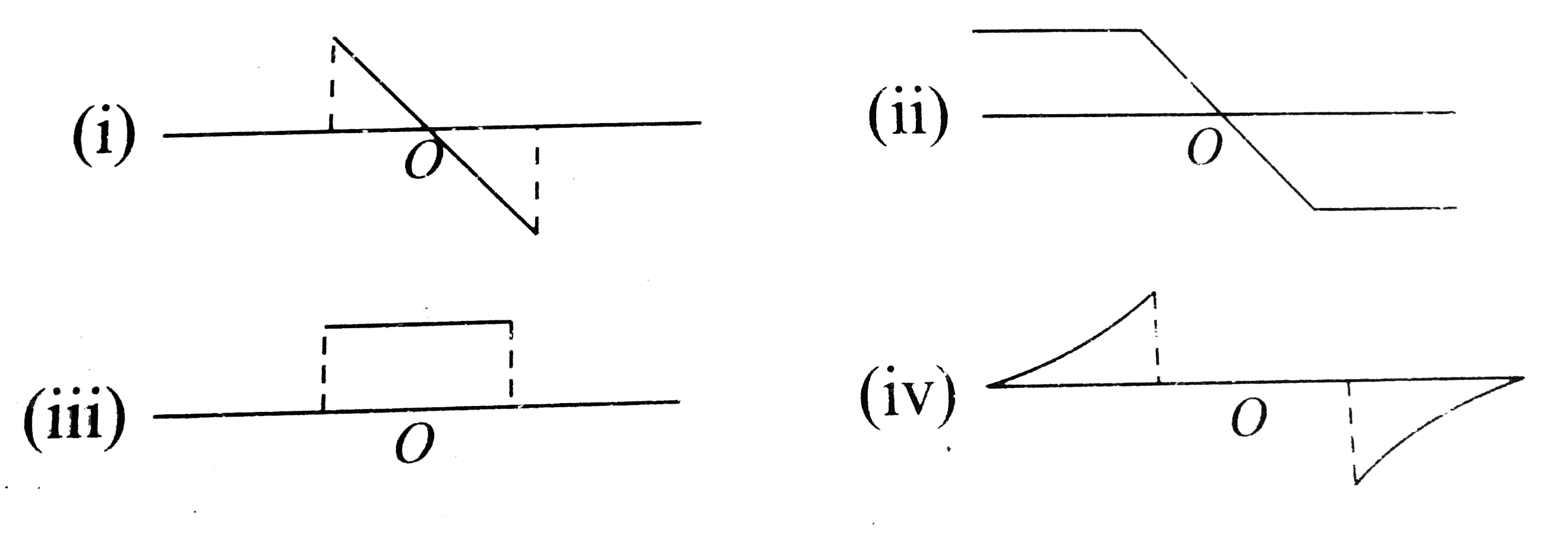 , (ii)
, (ii) 
(iii) , (iv)
, (iv)  .
.
Which graph best represents the plot of the electric potential (V) as a function of x (treating V = 0 at x = 0)?
View SolutionWe have two electric dipoles. Each dipole consists of two equal and opposite point charges at the ends of an insulating rod of length d. The dipoles sit along the x-axis a distance r apart oriented as shown in fig. Their separation `rgtgtd`. The dipole on the left:

View SolutionWe have two electric dipoles. Each dipole consists of two equal and opposite point charges at the ends of an insulating rod of length d. The dipoles sit along the x-axis a distance r apart oriented as shown in fig. Their separation `rgtgtd`. The dipole on the left:

View SolutionThe nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius r. The charge density `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
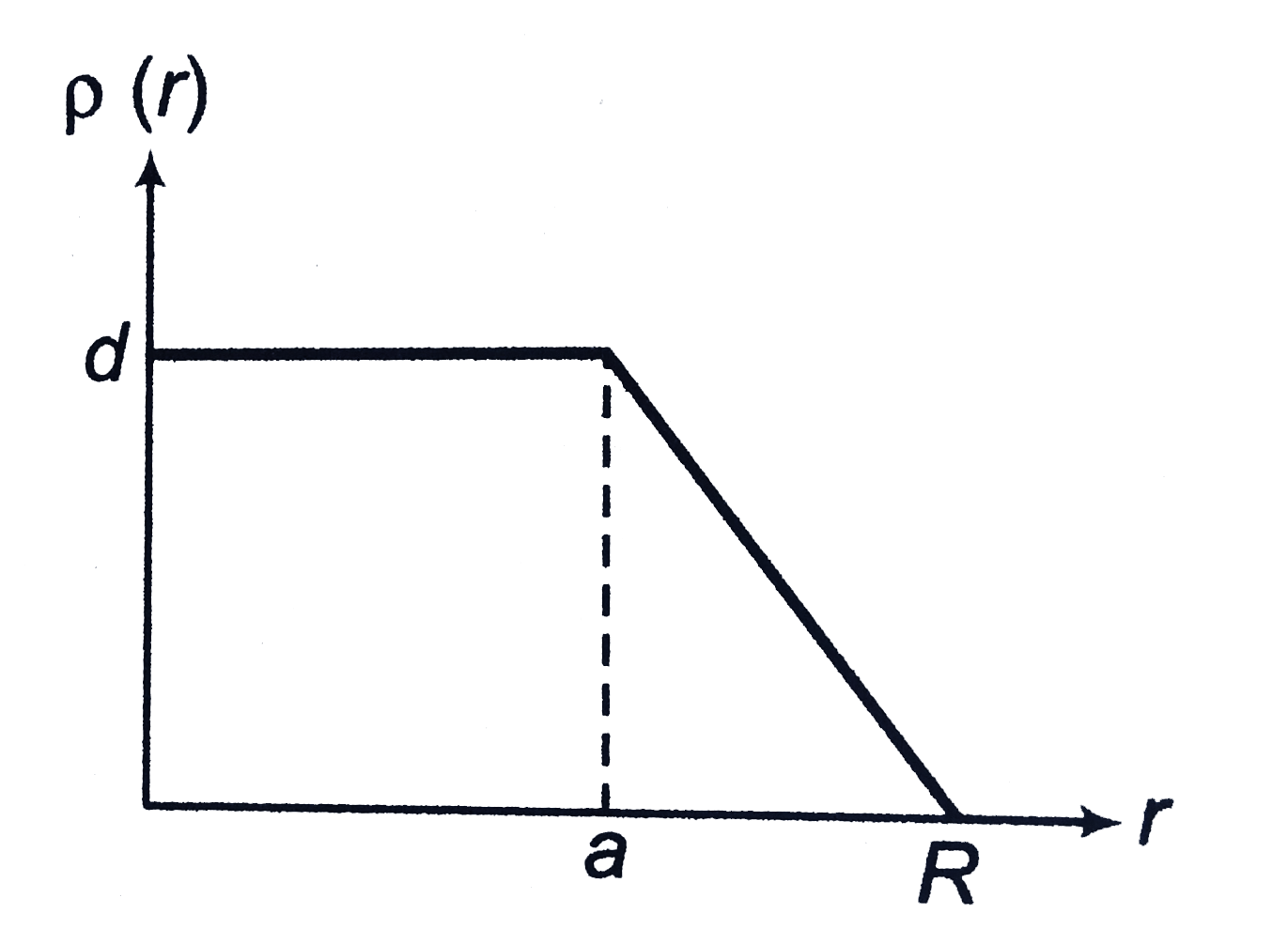
The electric field at `r=R` is
View SolutionThe nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius `r`. The charge density `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
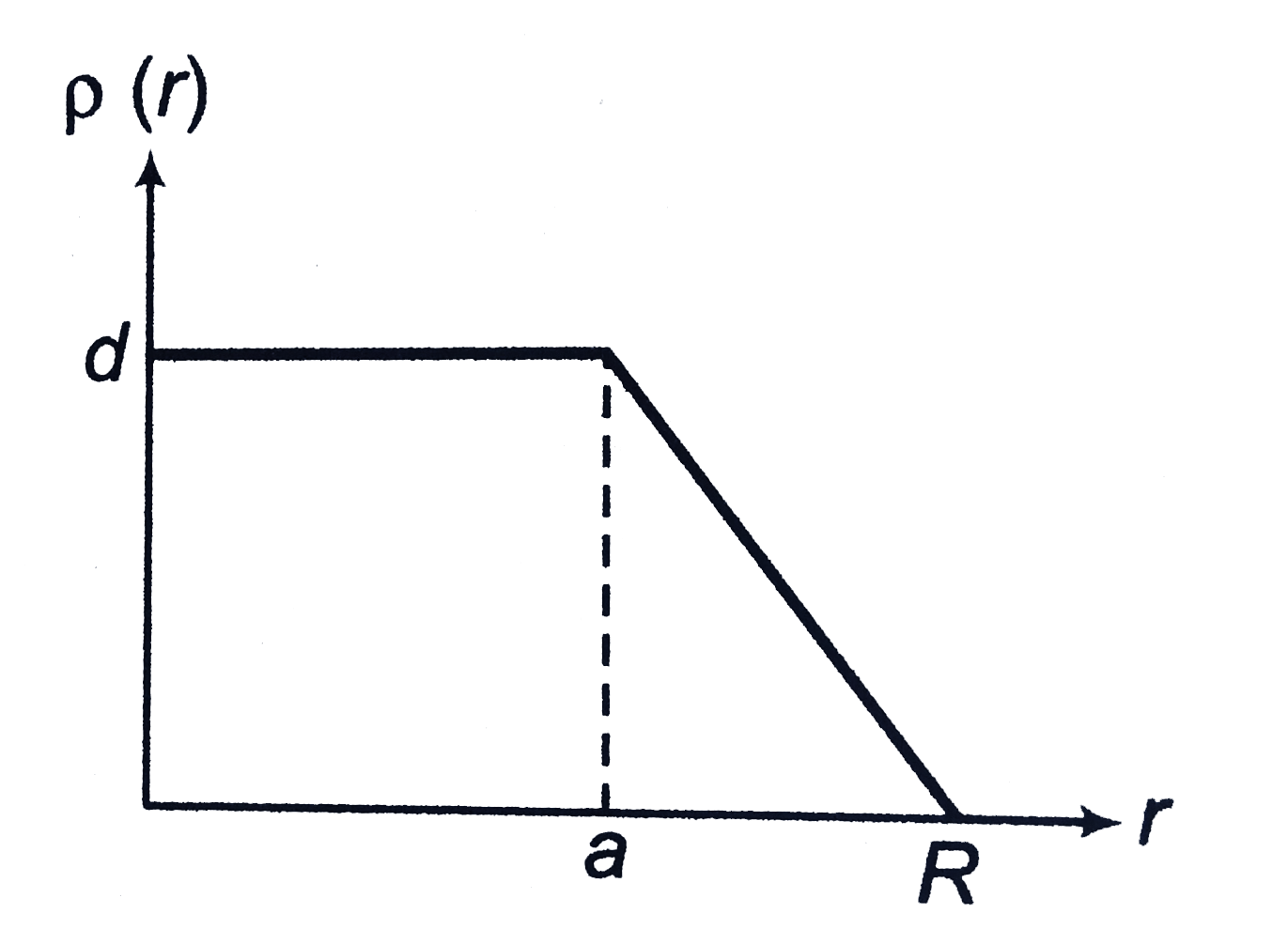
For a=0 the value of d (maximum value of `rho` as shown in the figure) is

View SolutionThe nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius r. The charge densilty `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
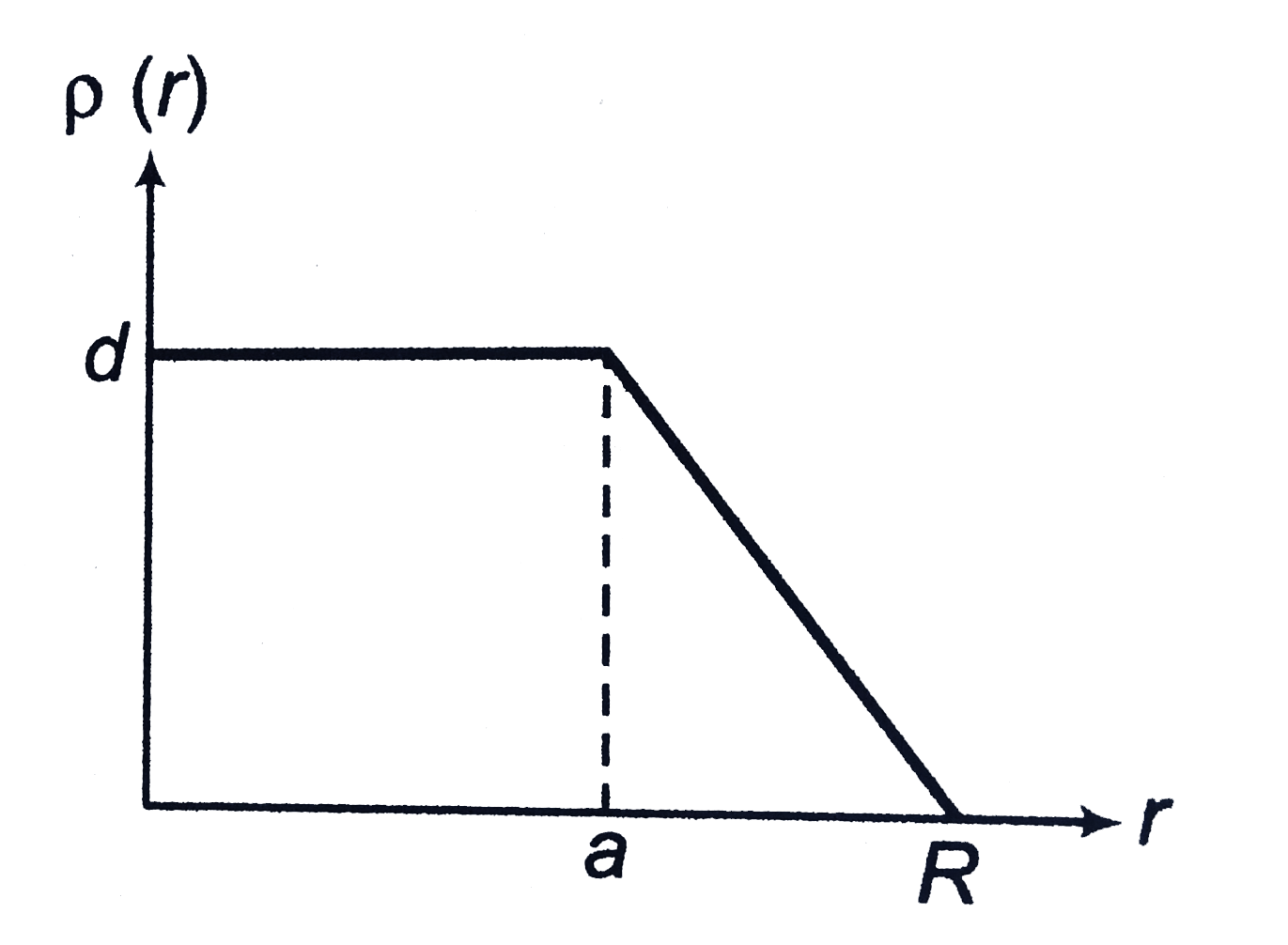
The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionA charge `+Q` is fixed at the origin of the co-ordinate system while a small electric dipole of dipolement `vecp` pointing away from the charge along the x-axis is set free from a point far away from the origin.
(a) Calculate the K.E. of the dipole when it reaches to a point (d, 0).
(b) Calculate the force on the charge `+Q` at this moment.
View SolutionA positive point charge q is fixed at origin. A dipole with a dipole moment `vecp` is placed along the x-axis far away from the origin with `vecp` pointing along the positive x-axis.
Find the kinetic energy of the dipole when it reaches a distance d from the origin.
View SolutionRam ans Shyam purchased two electric tea kettles A and B of same size, same thickness, and same volume of 0.4L. They studied the specification of kettles as under
`Kettle A: `
specific heat capacity `= 1680 Jkg^(-1)K^(-1)`
Mass = 200 g
Cost = Rs. 400
Kettle B:
Specific heat capacity = `2450 Jkg^(-1) K^(-1)`
Mass = 400 g
Cost = Rs. 400
When kettle A is switched on with constant potential source, the tea begins to boil in 6 min. When kettle B is switched on with the same source separately, then tea begins to boil in 8 min. The efficiengy of kettle is defined as
(Energy used for liquid heating)/(Total energy supplied)
They made discussion on specification and efficiency of kettles and subsequently prepared a list of questions to draw the conclusions. Some of them are as under (assume specific heat of tea liquid as `4200J kg^(-1)K^(-1)` and density `1000 kgm^(-3)`
Efficiency of kettle A is
View SolutionRam ans Shyam purchased two electric tea kettles A and B of same size, same thickness, and same volume of 0.4L. They studied the specification of kettles as under
`Kettle A: `
specific heat capacity `= 1680 Jkg^(-1)K^(-1)`
Mass = 200 g
Cost = Rs. 400
Kettle B:
Specific heat capacity = `2450 Jkg^(-1) K^(-1)`
Mass = 400 g
Cost = Rs. 400
When kettle A is switched on with constant potential source, the tea begins to boil in 6 min. When kettle B is switched on with the same source separately, then tea begins to boil in 8 min. The efficiengy of kettle is defined as
(Energy used for liquid heating)/(Total energy supplied)
They made discussion on specification and efficiency of kettles and subsequently prepared a list of questions to draw the conclusions. Some of them are as under (assume specific heat of tea liquid as `4200J kg^(-1)K^(-1)` and density `1000 kgm^(-3)`
Efficiency of kettle B is .
View SolutionRam and Shyam purchased two electric tea kettles A and B of same size, same thickness, and same volume of 0.4L. They studied the specification of kettles as under
`Kettle A: `
specific heat capacity `= 1680 Jkg^(-1)K^(-1)`
Mass = 200 g
Cost = Rs. 400
Kettle B:
Specific heat capacity = `2450 Jkg^(-1) K^(-1)`
Mass = 400 g
Cost = Rs. 400
When kettle A is switched on with constant potential source, the tea begins to boil in 6 min. When kettle B is switched on with the same source separately, then tea begins to boil in 8 min. The efficiengy of kettle is defined as
(Energy used for liquid heating)/(Total energy supplied)
They made discussion on specification and efficiency of kettles and subsequently prepared a list of questions to draw the conclusions. Some of them are as under (assume specific heat of tea liquid as `4200J kg^(-1)K^(-1)` and density `1000 kgm^(-3)`
Ratio of efficiency consumed charges for one time boiling of tea in kettle A to that in kettle B is
View SolutionRam ans Shyam purchased two electric tea kettles A and B of same size, same thickness, and same volume of 0.4L. They studied the specification of kettles as under
`Kettle A: `
specific heat capacity `= 1680 Jkg^(-1)K^(-1)`
Mass = 200 g
Cost = Rs. 400
Kettle B:
Specific heat capacity = `2450 Jkg^(-1) K^(-1)`
Mass = 400 g
Cost = Rs. 400
When kettle A is switched on with constant potential source, the tea begins to boil in 6 min. When kettle B is switched on with the same source separately, then tea begins to boil in 8 min. The efficiengy of kettle is defined as
(Energy used for liquid heating)/(Total energy supplied)
They made discussion on specification and efficiency of kettles and subsequently prepared a list of questions to draw the conclusions. Some of them are as under (assume specific heat of tea liquid as `4200J kg^(-1)K^(-1)` and density `1000 kgm^(-3)`
If resistances of coil of kettles A and B are `R_(A) and R_(B)`, respectively, then we can say
View SolutionRam ans Shyam purchased two electric tea kettles A and B of same size, same thickness, and same volume of 0.4L. They studied the specification of kettles as under
`Kettle A: `
specific heat capacity `= 1680 Jkg^(-1)K^(-1)`
Mass = 200 g
Cost = Rs. 400
Kettle B:
Specific heat capacity = `2450 Jkg^(-1) K^(-1)`
Mass = 400 g
Cost = Rs. 400
When kettle A is switched on with constant potential source, the tea begins to boil in 6 min. When kettle B is switched on with the same source separately, then tea begins to boil in 8 min. The efficiengy of kettle is defined as
(Energy used for liquid heating)/(Total energy supplied)
They made discussion on specification and efficiency of kettles and subsequently prepared a list of questions to draw the conclusions. Some of them are as under (assume specific heat of tea liquid as `4200J kg^(-1)K^(-1)` and density `1000 kgm^(-3)`
If both the kettles are joined with the same source in series one after the other, then boiling starts in kettle A and kettle B after
View SolutionElectric fuse is a protective device used in series with an electric circuit or an electric appliance to save it from damage due to overheating porduced by strong current in the circuit or application. Fuse wire is generally made from an alloy of lead and tin, which has hifh resistance and low melting point. It is connected in series in an electric installation. If a circuit gets accidentally short-circuited, a large current flows, then fuse wire melts away, which causes a break in the circuit. The power through fuse (F') is equal to heat energy lost per unit area per unit time (h) (neglecting heat loses from ends of the wire).
`P = I^2R = h xx 2pirl [R = (rhol)/(pir^2)]`
where r and l are the length and radius of fuse wire, respectively.
A Battery is described by its emf (E) and internal resistance (r). Efficiency of battery `(eta)` is defined as the ratio of the output to the input power.
`eta = (Output power)/(Input power) xx 100%`
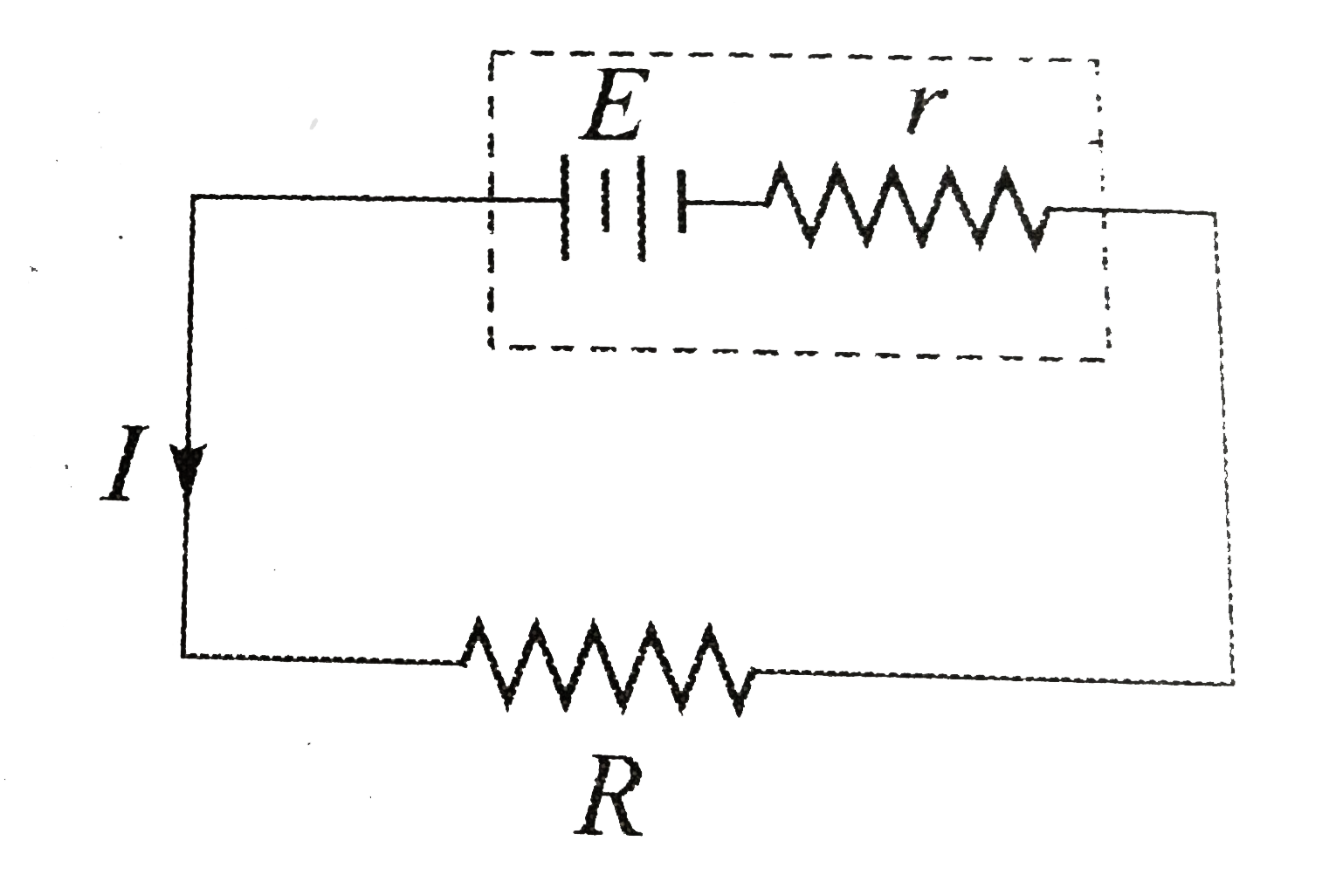
But `I= E//(R+r), ` input power = EI.
Output power `= EI - I^2r`, then.
`eta = ((EI - I^2r)/(EI)) xx 100 = (1-(Ir)/E) xx 100`
` =[1 - (E/(R+r)) (r/E)] xx 100 = (R/(R+r)) xx 100`
We know that output power of a source is maximum when the external resistance is equal to internal resistance, i.e., R = r .
Two fuse wires of same potential , material have length ratio `1:2` and ratio of radius `4:1`. Then respective ratio of their current rating will be
View SolutionElectric fuse is a protective device used in series with an electric circuit or an electric appliance to save it from damage due to overheating porduced by strong current in the circuit or application. Fuse wire is generally made from an alloy of lead and tin, which has hifh resistance and low melting point. It is connected in series in an electric installation. If a circuit gets accidentally short-circuited, a large current flows, then fuse wire melts away, which causes a break in the circuit. The power through fuse (F') is equal to heat energy lost per unit area per unit time (h) (neglecting heat loses from ends of the wire).
`P = I^2R = h xx 2pirl [R = (rhol)/(pir^2)]`
where r and l are the length and radius of fuse wire, respectively.
A Battery is described by its emf (E) and internal resistance (r). Efficiency of battery `(eta)` is defined as the ratio of the output to the input power.
`eta = (Output power)/(Input power) xx 100%`
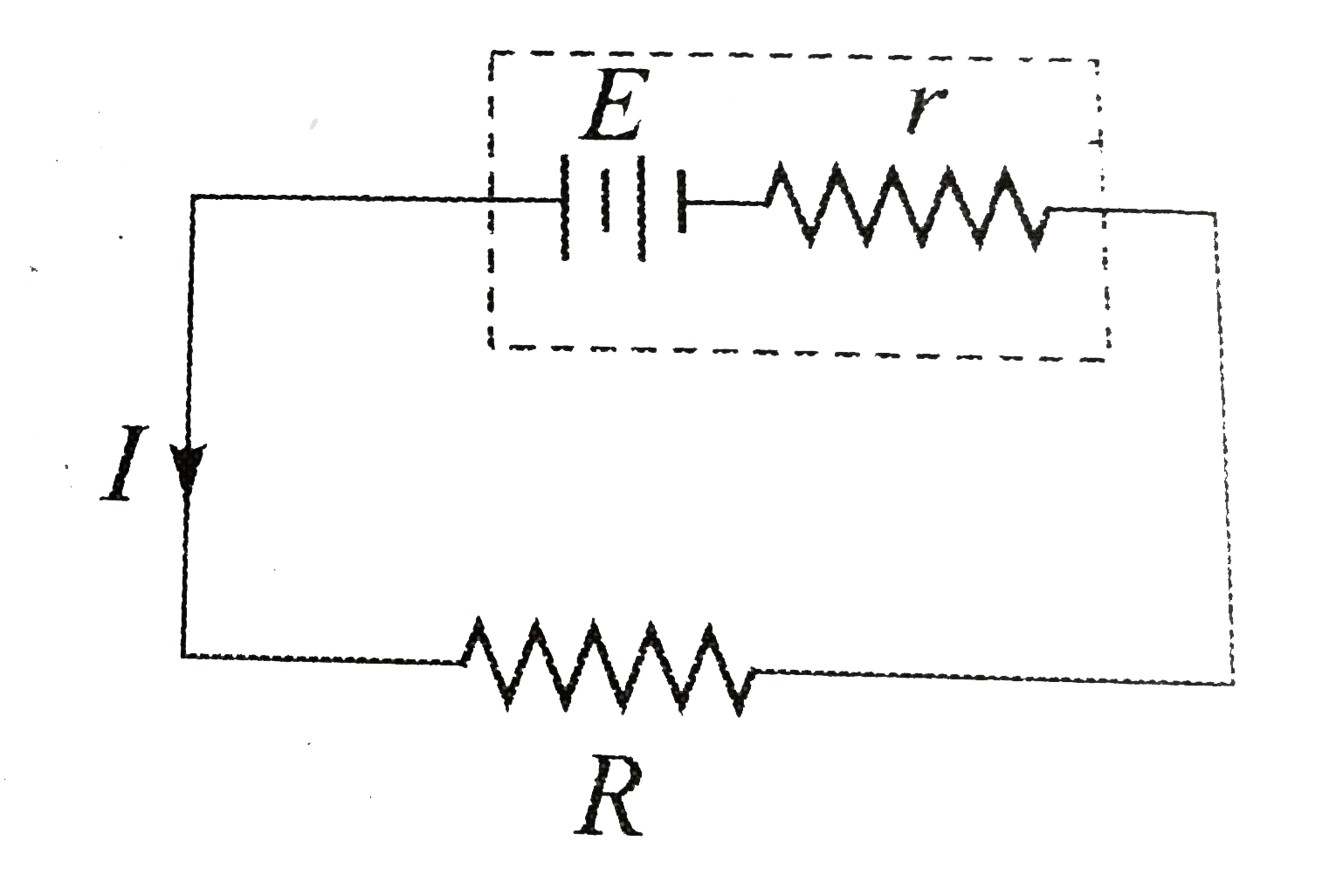
But `I= E//(R+r), ` input power = EI.
Output power `= EI - I^2r`, then.
`eta = ((EI - I^2r)/(EI)) xx 100 = (1-(Ir)/E) xx 100`
` =[1 - (E/(R+r)) (r/E)] xx 100 = (R/(R+r)) xx 100`
We know that output power of a source is maximum when the external resistance is equal to internal resistance, i.e., R = r .
The maximum power rating of a `20.0 Omega` fuse wire is `2.0 kW. ` This fuse wire can be connected safely to a DC source (negligible internal resistance) of
View SolutionElectric fuse is a protective device used in series with an electric circuit or an electric appliance to save it from damage due to overheating porduced by strong current in the circuit or application. Fuse wire is generally made from an alloy of lead and tin, which has hifh resistance and low melting point. It is connected in series in an electric installation. If a circuit gets accidentally short-circuited, a large current flows, then fuse wire melts away, which causes a break in the circuit. The power through fuse (F') is equal to heat energy lost per unit area per unit time (h) (neglecting heat loses from ends of the wire).
`P = I^2R = h xx 2pirl [R = (rhol)/(pir^2)]`
where r and l are the length and radius of fuse wire, respectively.
A Battery is described by its emf (E) and internal resistance (r). Efficiency of battery `(eta)` is defined as the ratio of the output to the input power.
`eta = (Output power)/(Input power) xx 100%`
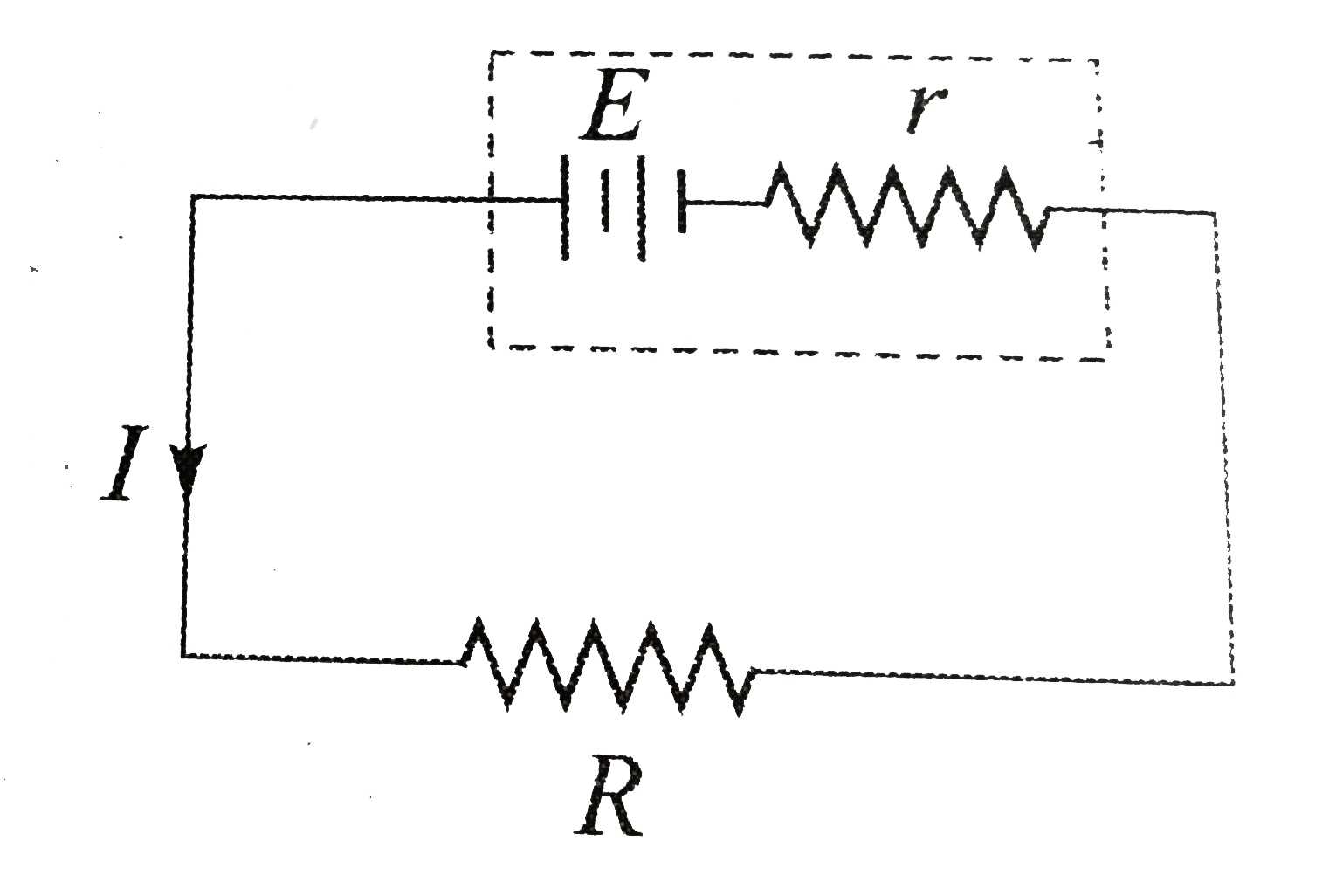
But `I= E//(R+r), ` input power = EI.
Output power `= EI - I^2r`, then.
`eta = ((EI - I^2r)/(EI)) xx 10 (1-(Ir)/E) xx 100`
` =1 - (E/(R+r)) (r/E) xx 100 = (R/(R+r)) xx 100`
We know that output power of a source is maximum when the external resistance is equal to internal resistance, i.e., R = r .
Efficiency of a battery (nonideal) when delivering the maximum power is
View SolutionIn the connection shown in the figure, initially the switch K is open and the capacitor is uncharged. Then the switch is closed, and the capacitor is charged up to the steady state and the switch is opened again. Determine the values indicated by the values indicated by the ammeter just after closing the switch
`[Given V_0 = 30 V, R_1 = 10k Omega, R_2 = 5kOmega`]
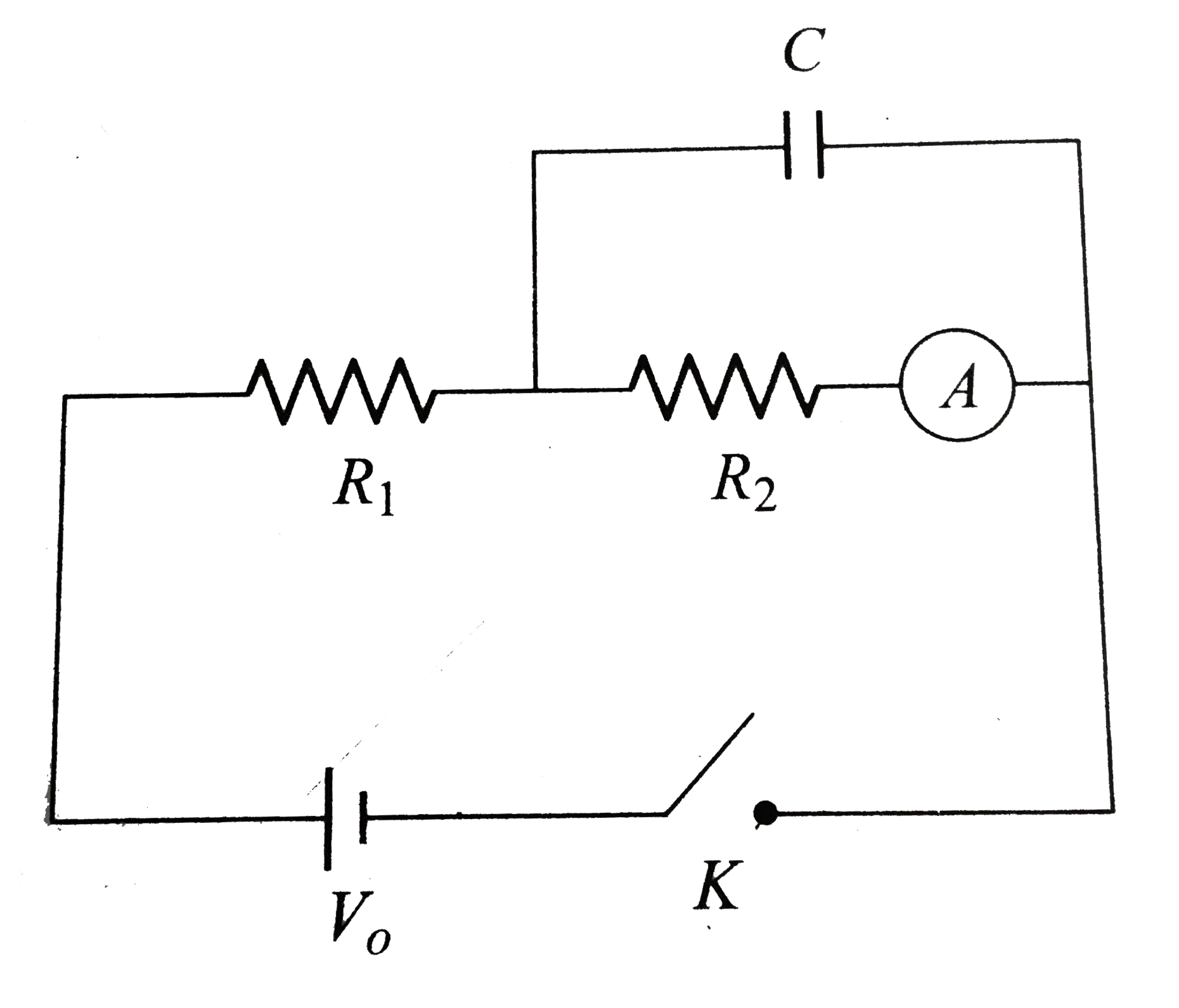 .
.
A long time after switch was closed.
View SolutionIn the connecting shows in Fig. 6.68, intially swich `K` is open and the capacitor is uncharged. Then the switch is closed and the capacitor is changed up to the steady state and the switch is opened again. Determine the values indicated by thee ammeter.
(Given : `V_(0) = 30 V`, `R_(1) = 10 k Omega`,

A long time after the swich was closed
View SolutionIn the connection shown in the figure, initially the switch K is open and the capacitor is uncharged. Then the switch is closed, and the capacitor is charged up to the steady state and the switch is opened again. Determine the values indicated by the values indicated by the ammeter just after closing the switch
`[Given V_0 = 30 V, R_1 = 10k Omega, R_2 = 5kOmega`]
 .
.
A long time after switch was closed.
View SolutionThe value of resistance of an unknown resistor is calculated using the formula `R = V//I ` where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter `(R_V and R_G, respectively)` are finite and nonzero.
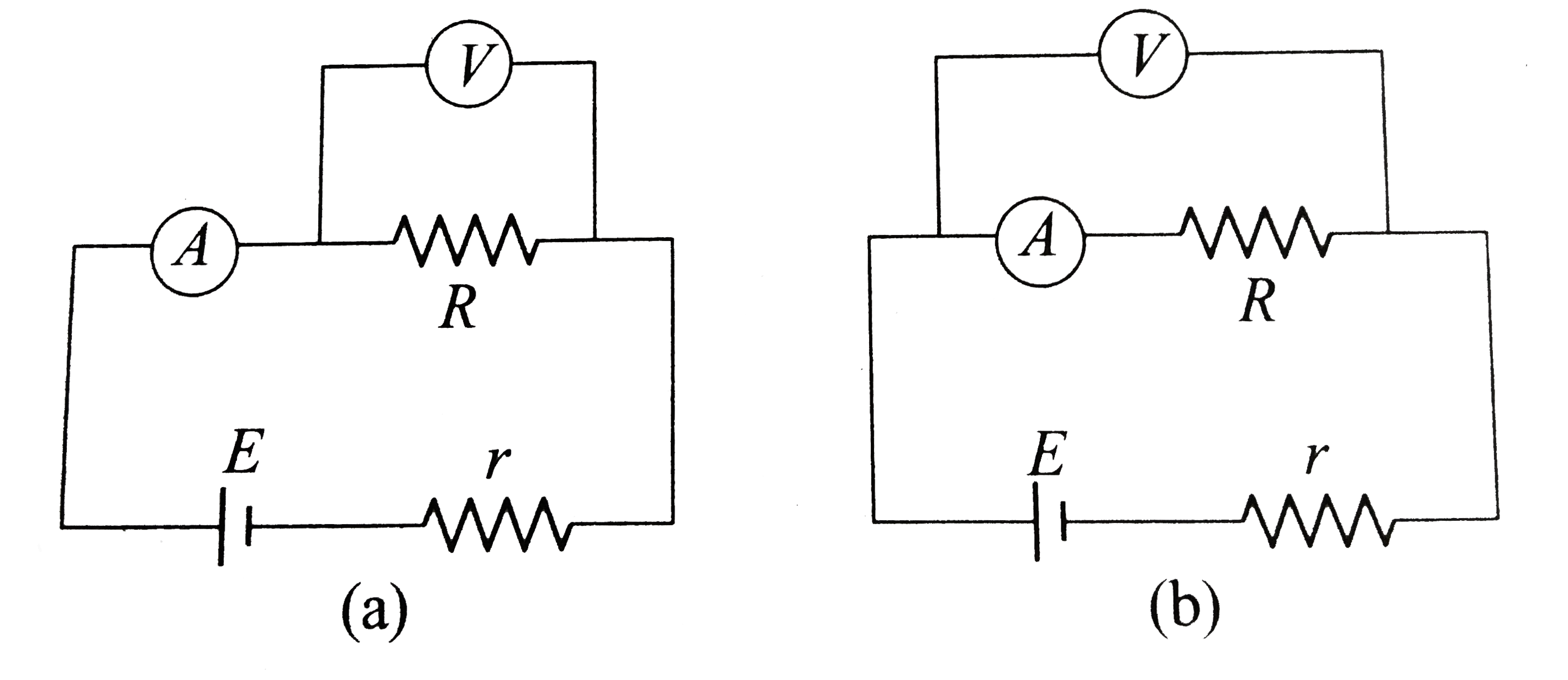 ,
,
Let `R_(A) and R_(B)` be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is `R_(V) = 1k Omega` and the percentage error in the measurement of R (the value of R is nearly `10 Omega`)is
View SolutionThe value of resistance of an unknown resistor is calculated using the formula `R = V//I ` where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter `(R_V and R_G, respectively)` are finite and nonzero.
 ,
,
Let `R_(A) and R_(B)` be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is `R_(V) = 1k Omega` and the percentage error in the measurement of R (the value of R is nearly `10 Omega`)is
View SolutionThe value of resistance of an unknown resistor is calculated using the formula `R = V//I ` where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter `(R_V and R_G, respectively)` are finite and nonzero.
 ,
,
Let `R_(A) and R_(B)` be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is `R_(V) = 1k Omega` and the percentage error in the measurement of R (the value of R is nearly `10 Omega`)is
View SolutionIn the circuit given in the figure, both batteries are ideal . Emf `E_1` of battery 1 has a fixed value, but emf `E_2` of battery 2 can be varied between `1.0V and 10.0 V` . The graph gives the currents through the two batteries as a function of `E_2` but are not marked as which plot corresponds to which battery. But for both plots, current is assumed to be negative when the direction of the current through the battery is opposite to the direction of that battery's emf (direction of emf is from negative to positive.)
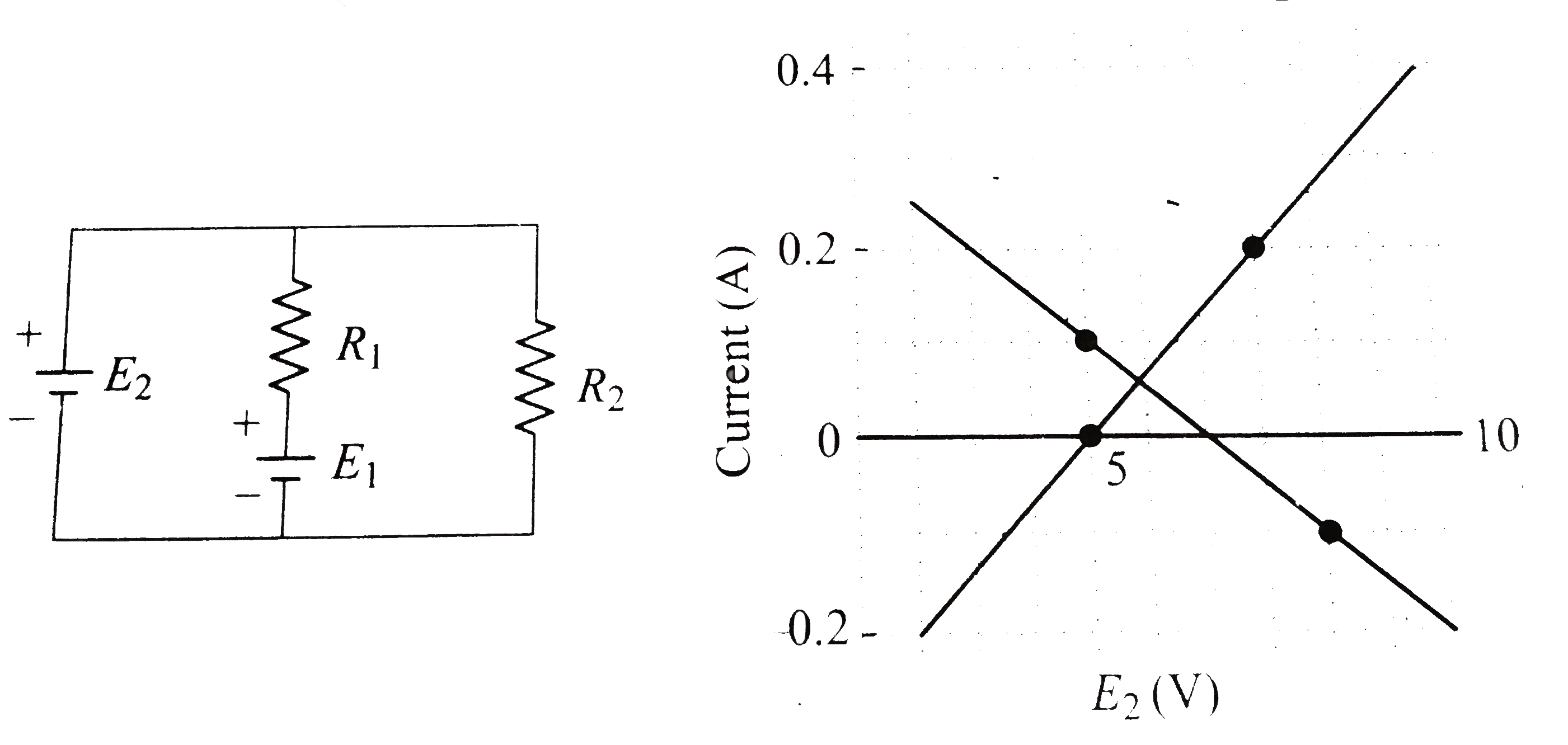
The value of emf `E_1` is
View SolutionIn the circuit given in the figure, both batteries are ideal . Emf `E_1` of battery 1 has a fixed value, but emf `E_2` of battery 2 can be varied between `1.0V and 10.0 V` . The graph gives the currents through the two batteries as a function of `E_2` but are not marked as which plot corresponds to which battery. But for both plots, current is assumed to be negative when the direction of the current through the battery is opposite to the direction of that battery's emf (direction of emf is from negative to positive.)
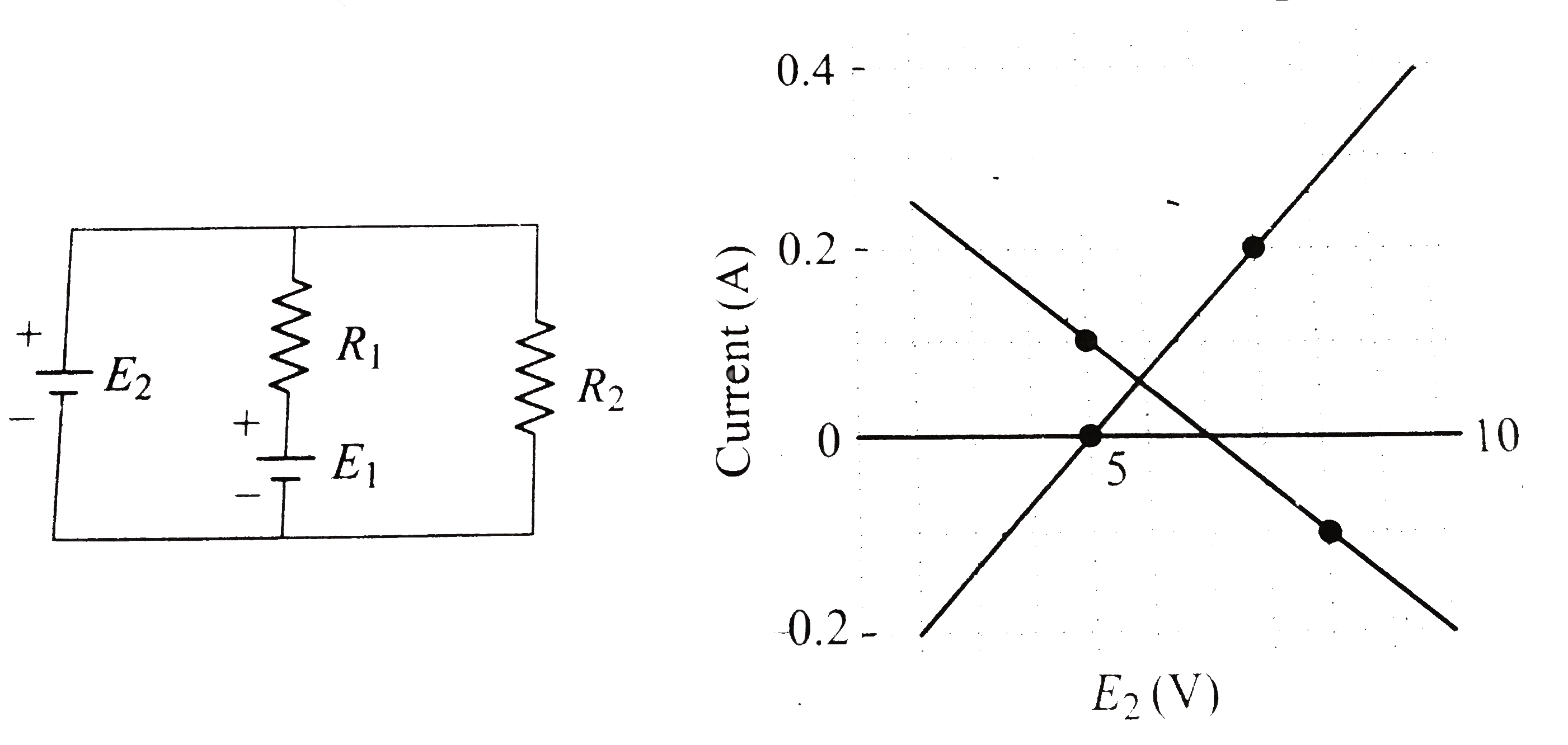 ,
,
The resistance `R_1` has value
View SolutionIn the circuit given in the figure, both batteries are ideal . Emf `E_1` of battery 1 has a fixed value, but emf `E_2` of battery 2 can be varied between `1.0V and 10.0 V` . The graph gives the currents through the two batteries as a function of `E_2` but are not marked as which plot corresponds to which battery. But for both plots, current is assumed to be negative when the direction of the current through the battery is opposite to the direction of that battery's emf (direction of emf is from negative to positive.)
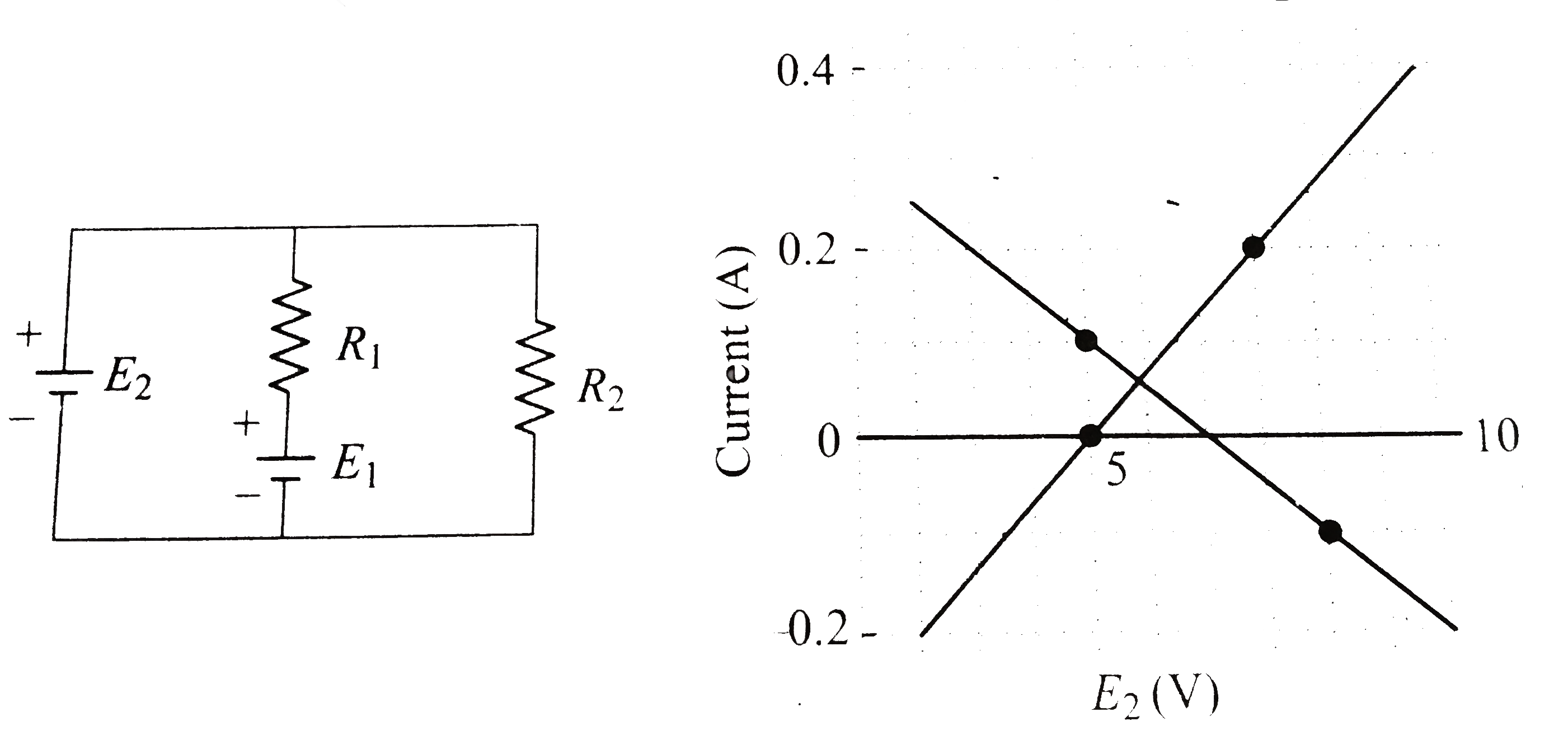 ,
,
The resistance `R_2` is equal to
View SolutionThe circuit is in a steady state.
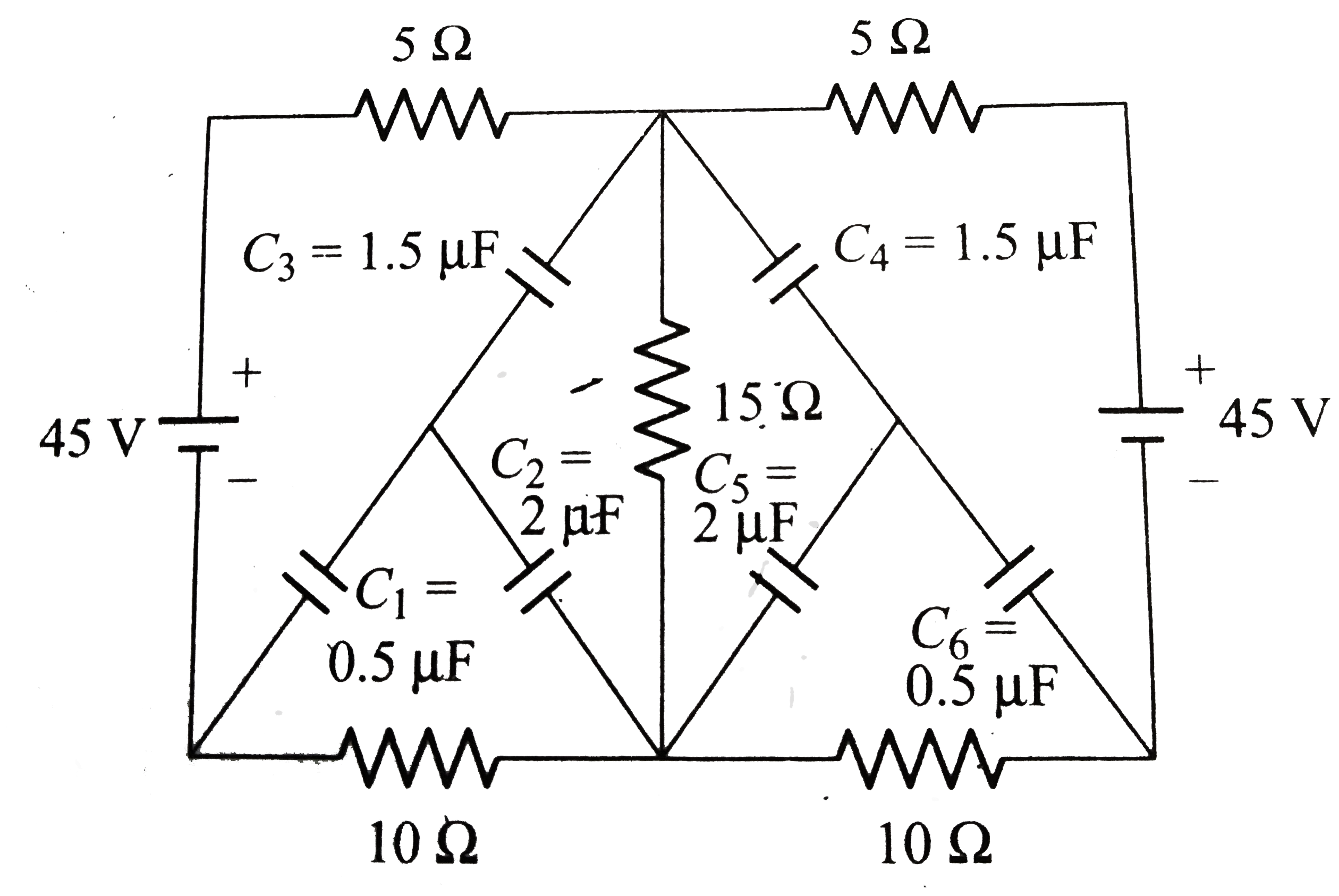
The charge in capacitor `C_1` is
View SolutionThe circuit is in a steady state.
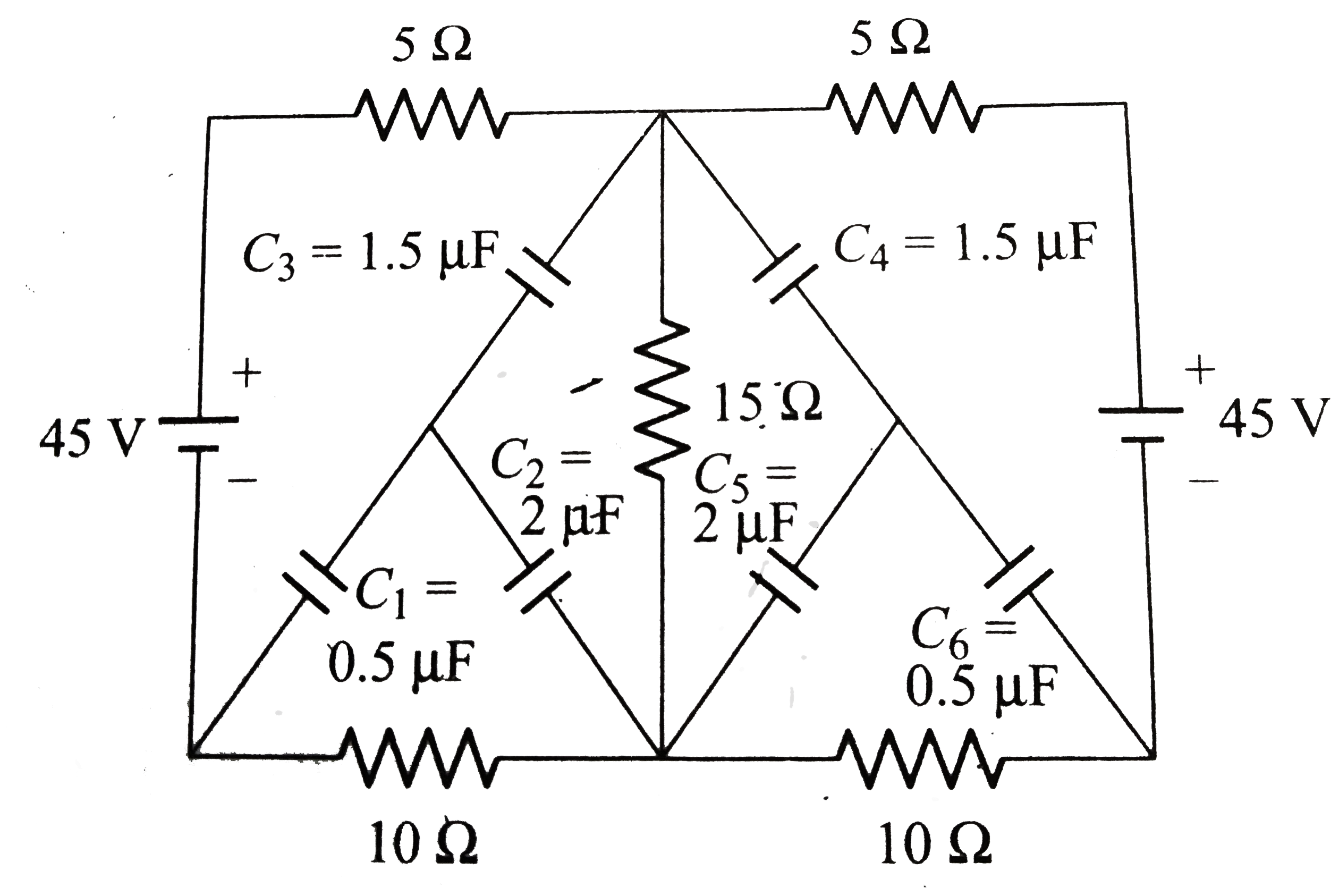
The charge in capacitor `C_2` is
View SolutionThe circuit is in a steady state.
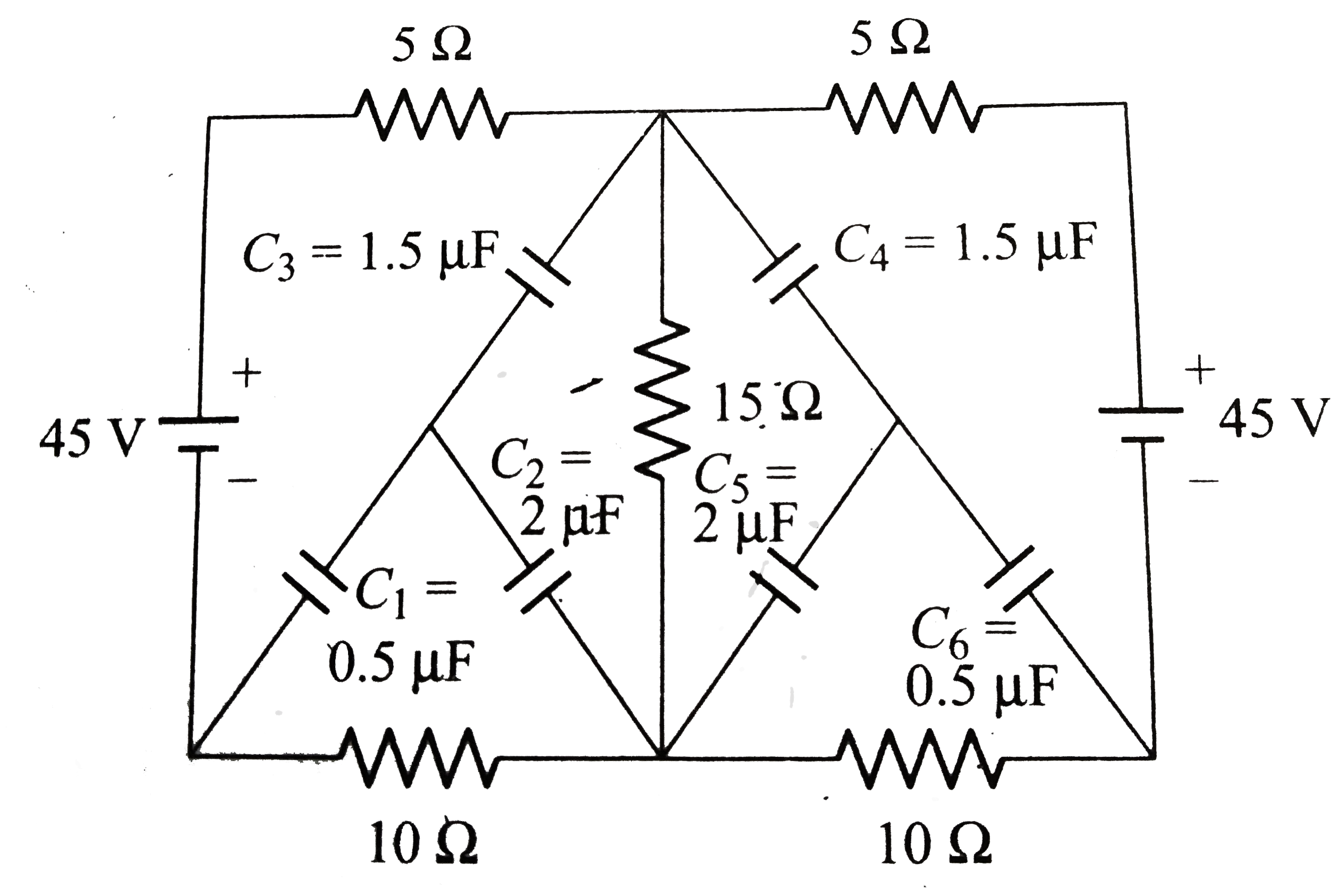
The charge in capacitor `C_3` is
View SolutionIn the circuit as shown, it is given that `R_1//R_2 = 1//2` and potential at O is V.
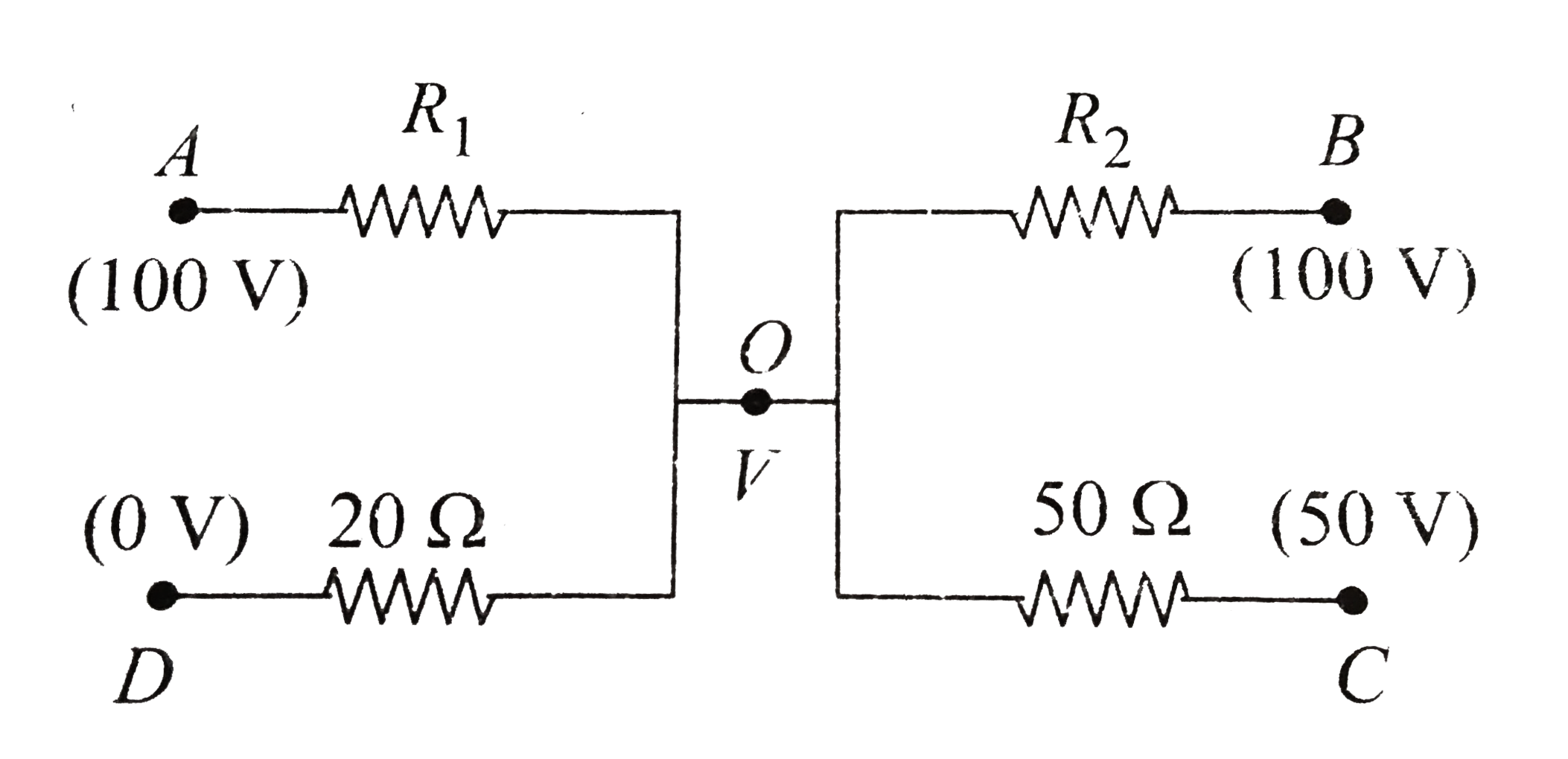
View SolutionIn the circuit as shown, it is given that `R_1//R_2 = 1//2` and potential at O is V.

View SolutionIn the circuit as shown, it is given that `R_1//R_2 = 1//2` and potential at O is V. The resistance `R_2` is-
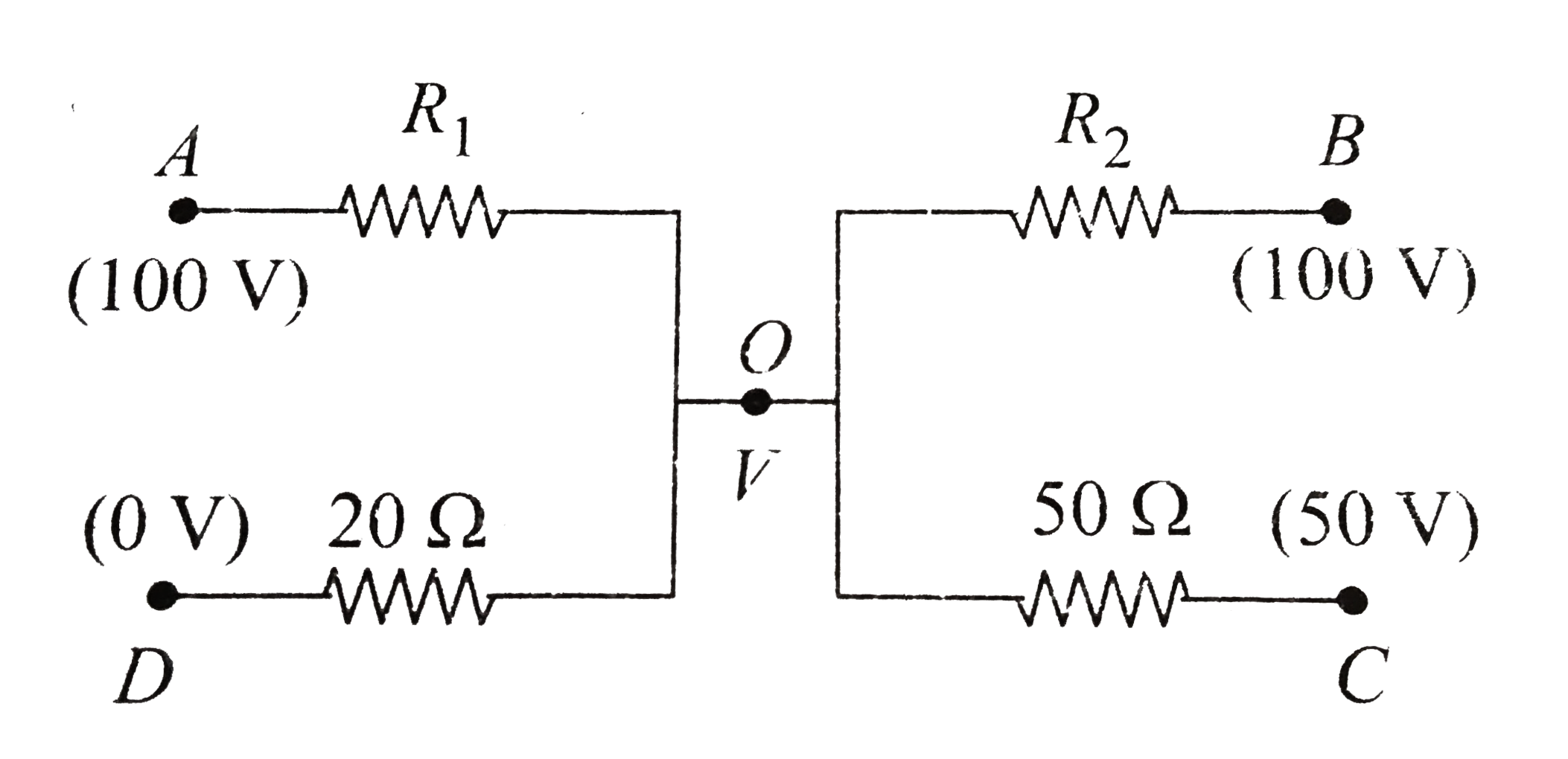
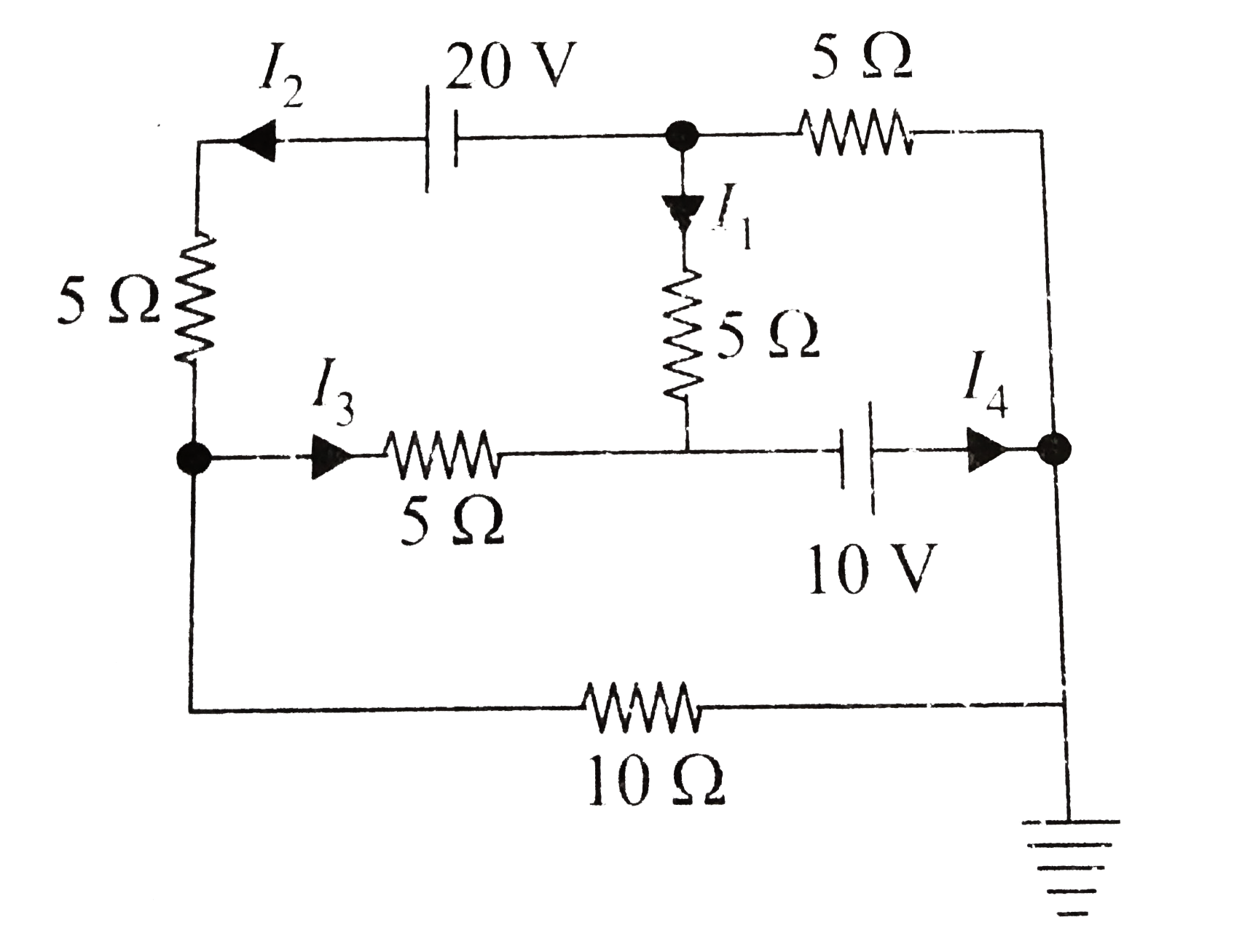
View SolutionIn the circuit shown in the figure
 .
.
The value of current `I_4` is
View SolutionIn the circuit shown in the figure
 .
.
The value of current `I_4` is
View SolutionAn ohm meter measures the resistance placed between its leads. This resistance reading is indicated by a galvanometer that operates on current. The ohm meter has an internal source of voltage to create the necessary current to operate the galvanometer and also has approproate resistor to allow just right amount of current through galvanometer. A simple ohm meter is shown here.
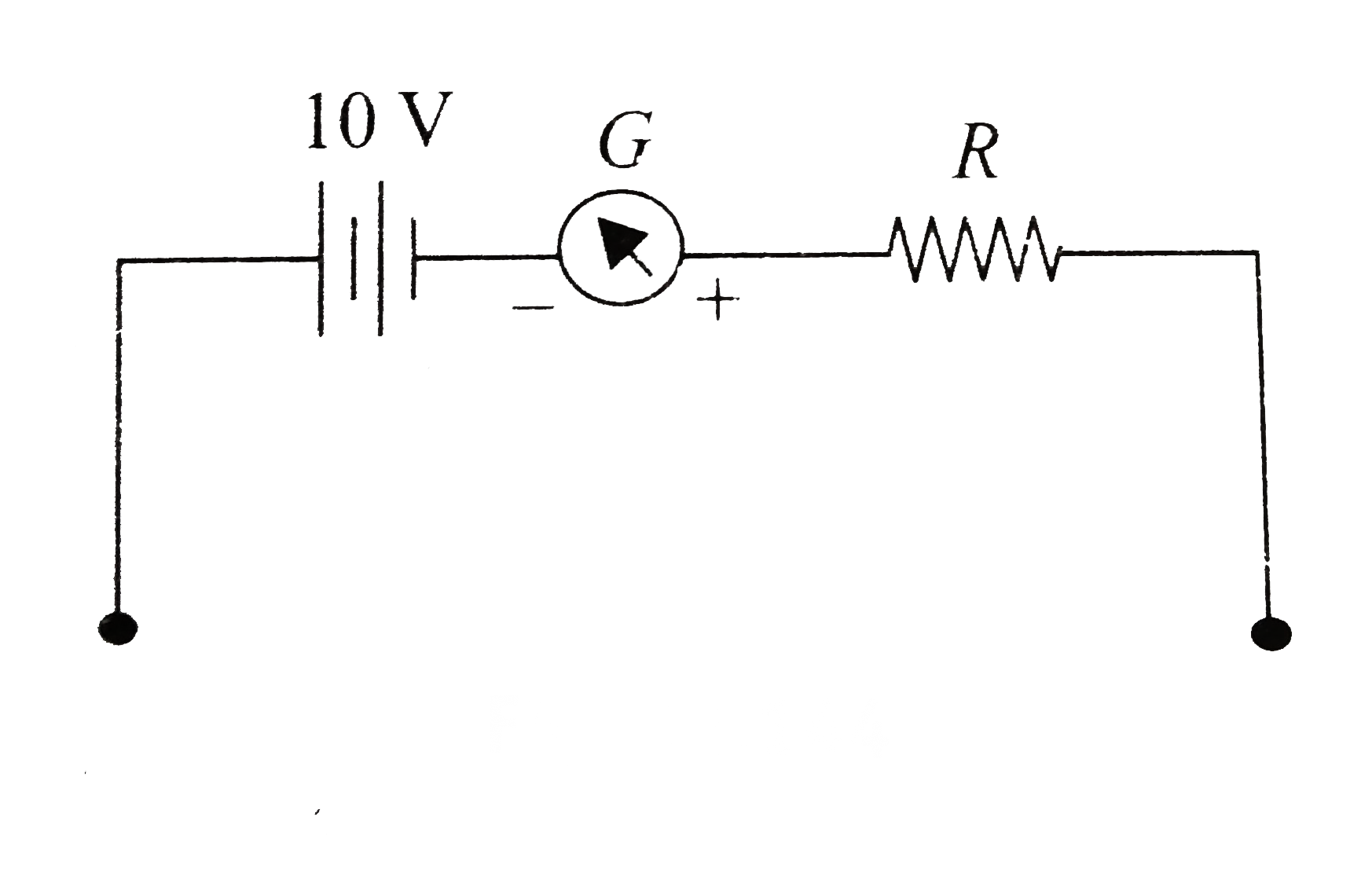
When there is an infinite resistance, there is zero current through galvanometer and it points in middle. If the test leads of this meter are directly shorted, (zero resistance) galvanometer will give full deflection.
Galvanometer specification
Resistance of galvanometer `= 100 Omega`
Fullscale current `= 0.5 mA`
Total number of division `=40` .
View SolutionAn ohm meter measures the resistance placed between its leads. This resistance reading is indicated by a galvanometer that operates on current. The ohm meter has an internal source of voltage to create the necessary current to operate the galvanometer and also has approproate resistor to allow just right amount of current through galvanometer. A simple ohm meter is shown here.
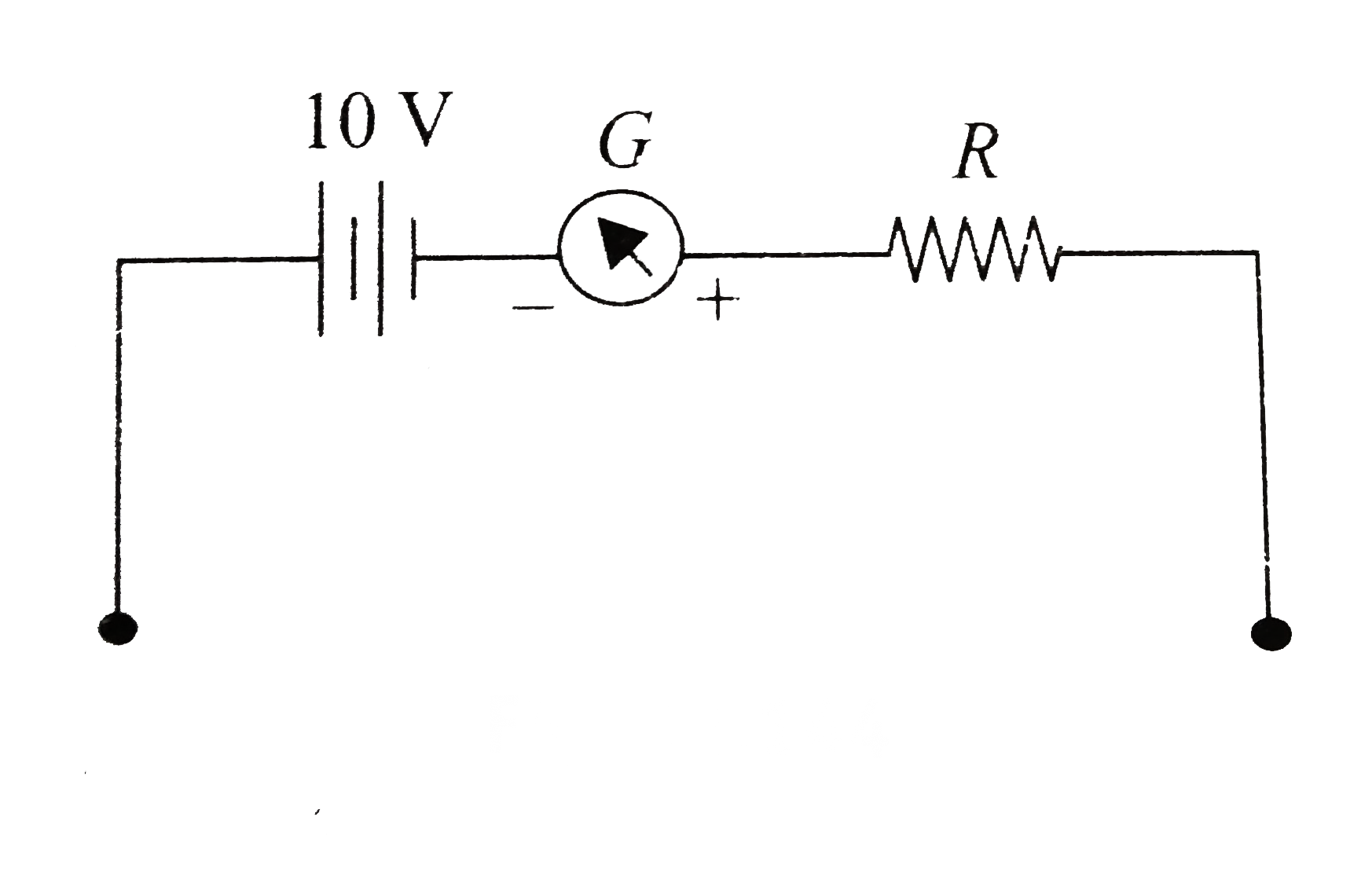
When there is an infinite resistance, there is zero current through galvanometer and it points in middle. If the test leads of this meter are directly shorted, (zero resistance) galvanometer will give full deflection.
Galvanometer specification
Resistance of galvanometer `= 100 Omega`
Fullscale current `= 0.5 mA`
Total number of division `=40` .
View SolutionAn ohm meter measures the resistance placed between its leads. This resistance reading is indicated by a galvanometer that operates on current. The ohm meter has an internal source of voltage to create the necessary current to operate the galvanometer and also has approproate resistor to allow just right amount of current through galvanometer. A simple ohm meter is shown here.
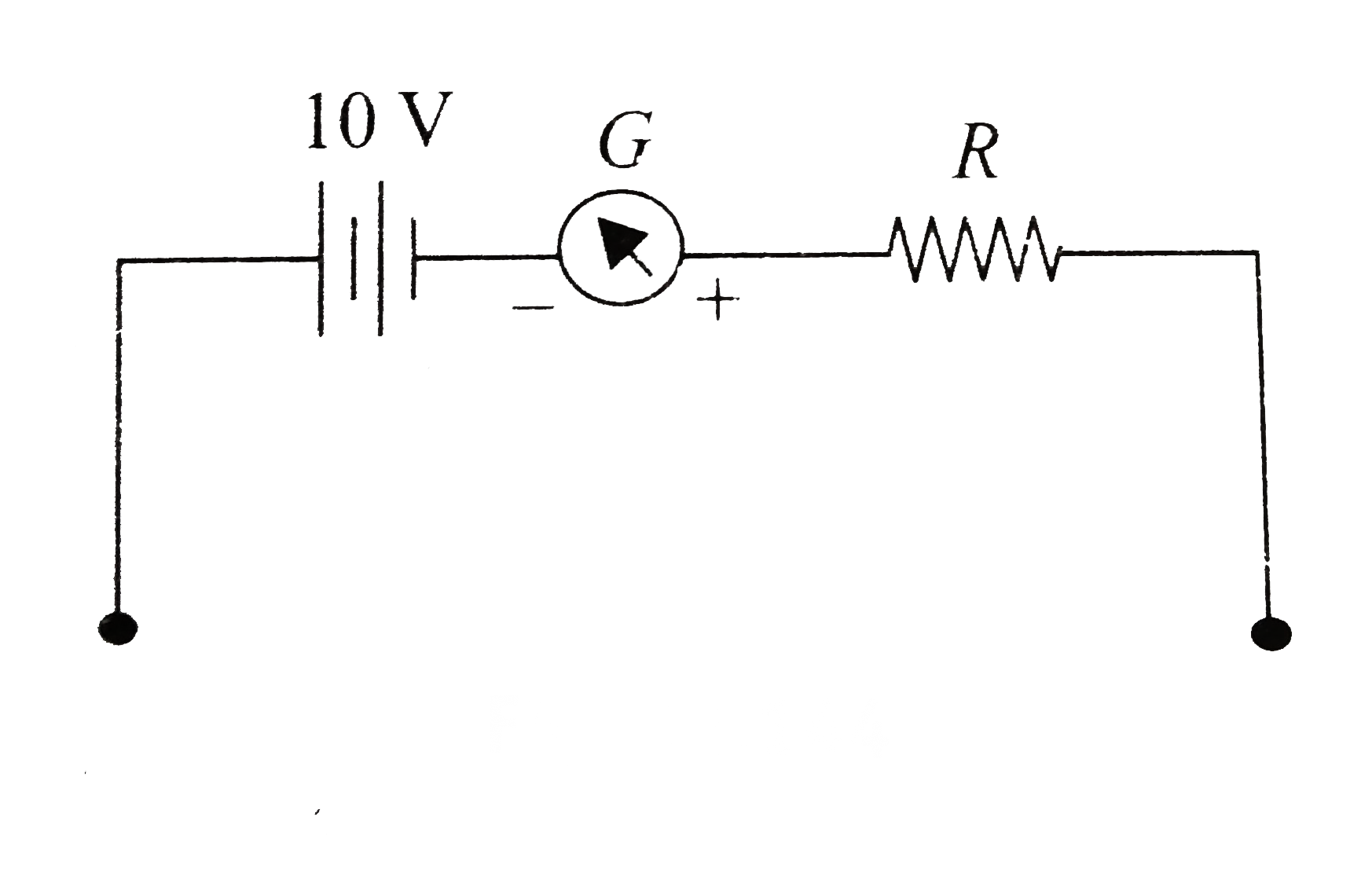
When there is an infinite resistance, there is zero current through galvanometer and it points in middle. If the test leads of this meter are directly shorted, (zero resistance) galvanometer will give full deflection.
Galvanometer specification
Resistance of galvanometer `= 100 Omega`
Fullscale current `= 0.5 mA`
Total number of division `=40` .
if we want to measure 5 Omega` Resistance than what is the position of needle
View Solution
Comprehension Type questions and complete solutions for chapter MISCELLANEOUS VOLUME 3 of CENGAGE PHYSICS (ENGLISH) of Class 12