Complete Solutions to Comprehension of chapter ELECTRIC FLUX AND GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC FLUX AND GAUSS LAW |
| CENGAGE PHYSICS | Comprehension |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
The cube shown in Fig. 2.119 has sides of length `L = 10.0 cm` . The electric field is uniform , has a magnitude `E = 4.00 xx 10^(3) NC^(-1) ` and is parallel to the `xy` plane at an angle of `37^(@)` measured from the `+ x - axis` toward the `+ y - axis` .

The surface that have zero flux are
View SolutionThe cube shown in Fig. 2.119 has sides of length `L = 10.0 cm` . The electric field is uniform , has a magnitude `E = 4.00 xx 10^(3) NC^(-1) ` and is parallel to the `xy` plane at an angle of `37^(@)` measured from the `+ x - axis` toward the `+ y - axis` .

Electric flux passing through surface `S_(1)` is
View SolutionThe cube shown in Fig. 2.119 has sides of length `L = 10.0 cm` . The electric field is uniform , has a magnitude `E = 4.00 xx 10^(3) NC^(-1) ` and is parallel to the `xy` plane at an angle of `37^(@)` measured from the `+ x - axis` toward the `+ y - axis` .

Electric flux passing through surface `S_(6)` is
View SolutionThe cube shown in Fig. 2.119 has sides of length `L = 10.0 cm` . The electric field is uniform , has a magnitude `E = 4.00 xx 10^(3) NC^(-1) ` and is parallel to the `xy` plane at an angle of `37^(@)` measured from the `+ x - axis` toward the `+ y - axis` .

The total net electric flux through all faces of the cube is
View SolutionA cube has sides of length `L = 0.300 m`. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by `vec( E) = ( -5.00 NC^(-1)) x hat(i) + (3.00 NC^(-1)) z hat(k)`.
The surface that have zero flux are
View SolutionA cube has sides of length `L = 0.300 m`. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by `vec( E) = ( -5.00 NC^(-1)) x hat(i) + (3.00 NC^(-1)) z hat(k)`.
The flux passing through the surface `S_(5)` will be
View SolutionA cube has sides of length `L = 0.300 m`. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by `vec( E) = ( -5.00 NC^(-1)) x hat(i) + (3.00 NC^(-1)) z hat(k)`.
The total flux passing through the cube is
View SolutionA cube has sides of length `L = 0.300 m`. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by `vec( E) = ( -5.00 NC^(-1)) x hat(i) + (3.00 NC^(-1)) z hat(k)`.
The total electric charge inside the cube is
View SolutionA cube has sides of length `L`. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by `vec€ = - B hat (i) + C hat (j) - D hat(k)` , where `B , C , and D` are positive constants.
The total flux passing through the cube is
View SolutionA cube of side `a` is placed such that the nearest face , which is parallel to the `yz` plane , is at a distance `a` from the origin . The electric field components are
`E_(x) = alpha x ^(1//2) , E_(y) = E_(z) = 0`.
The flux `phi_(E)` through the cube is

View SolutionA cube of side `a` is placed such that the nearest face , which is parallel to the `yz` plane , is at a distance `a` from the origin . The electric field components are
`E_(x) = alpha x ^(1//2) , E_(y) = E_(z) = 0`.
The charge within the cube is

View SolutionA small conducting spherical shell with inner radius `a` and outer radius `b` is concentric with a larger conducting spherical shell with inner radius `c` and outer radius `d` ( as shown in Fig . 2.121). The inner shell has a total charge ` + 2 q`, and the outer shell has a total charge ` + 4 q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for

`r lt a`
View SolutionA small conducting spherical shell with inner radius `a` and outer radius `b` is concentric with a larger conducting spherical shell with inner radius `c` and outer radius `d` ( as shown in Fig . 2.121). The inner shell has a total charge ` + 2 q`, and the outer shell has a total charge ` + 4 q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for

`a lt r lt b`
View SolutionA small conducting spherical shell with inner radius `a` and outer radius `b` is concentric with a larger conducting spherical shell with inner radius `c` and outer radius `d` ( as shown in Fig . 2.121). The inner shell has a total charge ` + 2 q`, and the outer shell has a total charge ` + 4 q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for

`b lt r lt c`
View SolutionA small conducting spherical shell with inner radius `a` and outer radius `b` is concentric with a larger conducting spherical shell with inner radius `c` and outer radius `d` ( as shown in Fig . 2.121). The inner shell has a total charge ` + 2 q`, and the outer shell has a total charge ` + 4 q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for

`c lt r ltd`
View SolutionA small conducting spherical shell with inner radius `a` and outer radius `b` is concentric with a larger conducting spherical shell with inner radius `c` and outer radius `d` ( as shown in Fig . 2.121). The inner shell has a total charge ` + 2 q`, and the outer shell has a total charge ` + 4 q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for

`r gt d`
View SolutionA small conducting spherical shell with inner radius `a` and outer radius `b` is concentric with a larger conducting spherical shell with inner radius `c` and outer radius `d` ( as shown in Fig . 2.121). The inner shell has a total charge ` + 2 q`, and the outer shell has a total charge ` + 4 q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for

The graph of the radial component of `E` as a function of `r` will be
View SolutionConsider the previous problem , let the outer shell have the charge ` - 4 q`. As in the above problem , the inner shell has the charge ` + 2q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for
`r lt a`
View SolutionConsider the previous problem , let the outer shell have the charge ` - 4 q`. As in the above problem , the inner shell has the charge ` + 2q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for
`a lt r lt b`
View SolutionConsider the previous problem , let the outer shell have the charge ` - 4 q`. As in the above problem , the inner shell has the charge ` + 2q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for
`b lt r lt c`
View SolutionConsider the previous problem , let the outer shell have the charge ` - 4 q`. As in the above problem , the inner shell has the charge ` + 2q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for
The graph of the radial component of `E` as function of `r` will be
View SolutionConsider the previous problem , let the outer shell have the charge ` - 4 q`. As in the above problem , the inner shell has the charge ` + 2q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for
`c lt r lt d`
View SolutionConsider the previous problem , let the outer shell have the charge ` - 4 q`. As in the above problem , the inner shell has the charge ` + 2q`. Calculate the electric field in terms of `q` and the distance `r` from the common center of the two shells for
View SolutionTwo spherical cavities of radii `a` and `b` are hollowed out from the interior of a neutral conducting sphere of radius `R`. At the center of each cavity , a point charge is placed . Call these charges `q_(a)` and `q_(b)`.
The electric field at a distance `r` outside the conductor is

View SolutionTwo spherical cavities of radii `a` and `b` are hollowed out from the interior of a neutral conducting sphere of radius `R`. At the center of each cavity , a point charge is placed . Call these charges `q_(a)` and `q_(b)`.
The electric field inside the cavity of radius `a` at a distance `r` from the center of cavity is

View SolutionPositive and negative charges of equal magnitude lie along the symmetry axis of a cylinder. The distance from the positive charge to the left - end cap of the cylinder is the same as the distance from the negative charge to the right - end cap.

What is the flux of the electric field through the closed cylinder ?
View SolutionPositive and negative charges of equal magnitude lie along the symmetry axis of a cylinder. The distance from the positive charge to the left - end cap of the cylinder is the same as the distance from the negative charge to the right - end cap.

What is the sign of the flux through the right - end cap of the cylinder ?
View SolutionThere are two nonconducting spheres having uniform volume charge densities `rho` and `- rho` . Both spheres have equal radius `R`. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take `vec(d) = O_(1) vec(O_(2))`.

The electric field `vec(E)` in the overlapped region is
View SolutionThere are two nonconducting spheres having uniform volume charge densities `rho` and `- rho` . Both spheres have equal radius `R`. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take `vec(d) = O_(1) vec(O_(2))`.

The potential difference `Delta V` between the centres of the two spheres for `d = R` is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is `epsilon_(0) phi = q_(encl)`,when `q(encl)` is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point `P` on the surface are
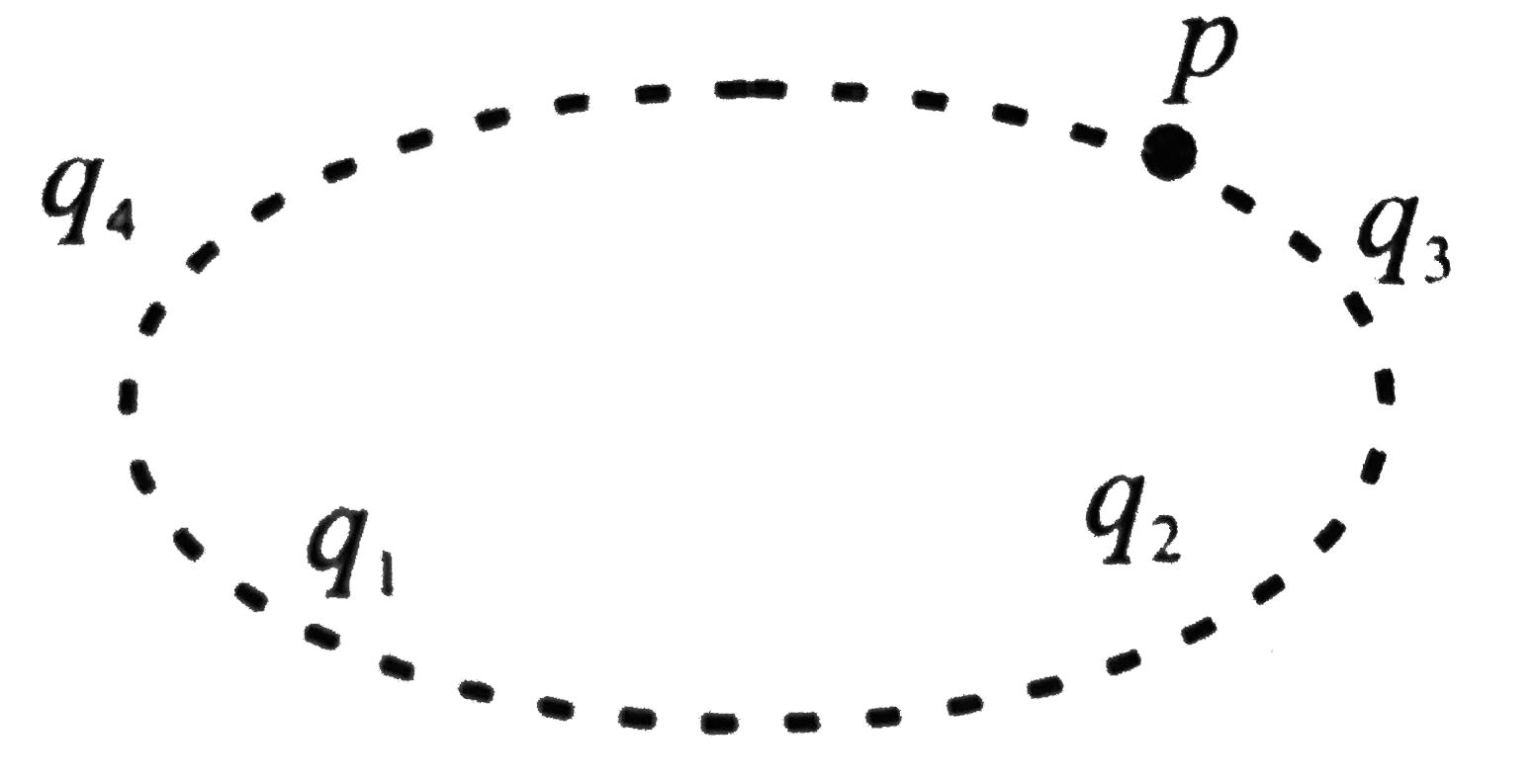
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is `epsilon_(0) phi = q_(encl)`,when `q(encl)` is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is `epsilon_(0) phi = q_(encl)`,when `q(encl)` is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to `q_(3)` and `q_(4)` is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is `epsilon_(0) phi = q_(encl)`,when `q(encl)` is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge `q_(3)` and `q_(4)` are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
`A`: Electric field at each point on the Gaussian surface will remain same .
`B`: The value of `oint vec(E ) .d vec(A)` for the Gaussian surface will remain same.
View SolutionA spherical conductor `A` contains two spherical cavities as shown in Fig. The total charge on conductor itself is zero . However , there is a point charge `q_(1)` at the center of one cavity and `q_(2)` at the center of the other cavity . Another charge `q_(3)` is placed at a large distance `r` from the center of the spherical conductor.

Which of the following statements are true ?
View SolutionA spherical conductor `A` contains two spherical cavities as shown in Fig.2.127. The total charge on conductor itself is zero . However , there is a point charge `q_(1)` at the center of one cavity and `q_(2)` at the center of the other cavity . Another charge `q_(3)` is placed at a large distance `r` from the center of the spherical conductor.

If `q_(1)` is displaced from its center slightly (being always inside the same cavity ), then the correct representation of field lines inside the same cavity is
View SolutionA spherical conductor `A` contains two spherical cavities as shown in Fig.2.127. The total charge on conductor itself is zero . However , there is a point charge `q_(1)` at the center of one cavity and `q_(2)` at the center of the other cavity . Another charge `q_(3)` is placed at a large distance `r` from the center of the spherical conductor.

The force acting on conductor `A` will be
View Solution
Comprehension questions and complete solutions for chapter ELECTRIC FLUX AND GAUSS LAW of CENGAGE PHYSICS (HINGLISH) of Class 12