Complete Solutions to Single Correct of chapter ELECTRIC FLUX AND GAUSS LAW of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC FLUX AND GAUSS LAW |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
A cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is `vecE = 200hati`. Find the flux through the left end of the cylinder.
View SolutionConsider the Gaussian surface that surrounds parts of the charge distribution shown in figure. Then the contribution to the electric field at point P arises from charges

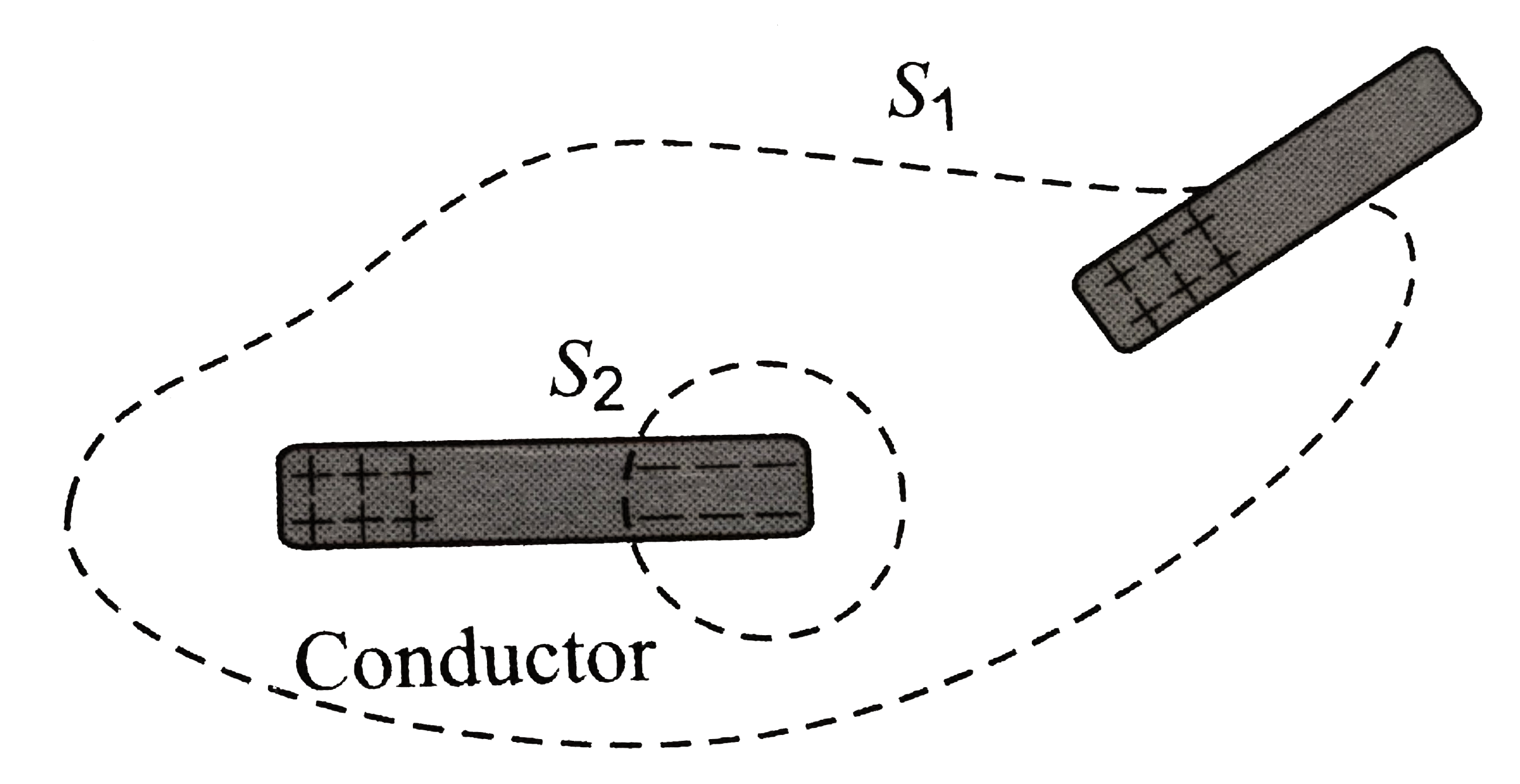
View SolutionCharge on an originally uncharged conductor is separated by holding a positively charged rod very closely nearby, as shown in figure. Assume that the induced negative charge on the conductor is equal to the positive charge q on the rod. Then the flux through surface `S_1` is
View SolutionA thin. Metallic spherical shell contains s charge Q on it. A point charge q is placed at the centre of the shell and another charge `q_1` is placed outside it as shown in figure (30-Q1). All the three charges are positive. The force on the charge at the centre is

View SolutionAn uncharged metal sphere is placed between two equal and oppositely charged metal plates. The nature of lines of force will be
View SolutionA hollow metallic sphere of radius 10 cm is given a charge of `3.2 xx 10^(-9) C.` The electric intensity at a point 4 cm from the center is
View SolutionThe surface density on a copper sphere is `sigma`. The electric field strength on the surface of the sphere is
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionA cube of side 10 cm encloses a charge of `0.1 muC` at its center. Calculate the number of lines of force through each face of the cube.
View SolutionThe electric flux from a cube of edge l is `phi`. If the edge of the cube is made `2l` and the charge enclosed is halved, its value will be
View SolutionIn a certain region of space, there exists a uniform electric field of value ` 2xx 10^2hatkVm^(-1)`. A rectangular coil of dimension `10 cm xx 20 cm ` is placed in the xy plane. The electric flux through the coil is
View SolutionConsider two concentric spherical surfaces `S_1` with radius a and `S_2` with radius 2a, both centered at the origin. There is a charge +q at the origin and there are no other charges. Compare the flux `phi_1` through `S_1` with the flux `phi_2` through `S_2`.
View SolutionUnder what conditions can the electric flux `phi_E` be found through a closed surface?
View SolutionFigure shows four charges `q_1,q_2,q_3,and q_4` fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is

View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionEight charges, 1muC, -7muC , -4muC, 10muC, 2muC, -5muC, -3muC, and 6muC`, are situated at the eight cornersof a cube of side 20 cm. A spherical surface of radius 80 cm encloses this cube. The center of the sphere coincides with the center of the cube. Then, the total outgoing flux from the spherical surface (in units of Vm) is
View SolutionThree charges `q_1 = 1 xx 10^(-6) C, q^2 = 2 xx 10^(-6)C, and q_3 = -3 xx 10^(-6) C ` have been placed as shown in figure. Then the net electric flux will be maximum for the surface

View SolutionIn a region of space, the electric field is given by `vecE = 8hati + 4hatj + 3hatk`. The electric flux through a surface of area 100 units in the xy plane is
View SolutionA spherical shell of radius `R = 1.5 cm` has a charge `q = 20muC` uniformly distributed over it. The force exerted by one half over the other half is
View SolutionA flat, square surface with sides of length L is described by the equations
`x = L, 0le y leL,0lezleL`
The electric flux through the square due to a positive point charge q located at the origin `(x = 0 , y = 0, z = 0)` is
View SolutionThe electric field `vecE_1` at one face of a parallelopiped is uniform over the entire face and is directed out of the face. At the opposite face, the electric field `vecE_2` is also uniform over the entire face and is directed into that face (as shown in figure). The two faces in question are inclined at `30^@` from the horizontal, `vecE_1 and vecE_2`(both horizontal) have magnitudes of `2.50 xx 10^(4) NC^(-1)` and `7.00 xx 10^(4)NC^(-1)`. respectively. Assuming that no other electric field lines cross the surfaces of the parallelopiped, the net charge contained with in is

View SolutionA dielectric in the form of a sphere is introduced into a homogeneous electric field. A, B, and C are three pointsas shown in figure. Then

View SolutionThe electric field on two sides of a large charged plate is shown in figure. The charge density on the plate in SI units is given by `(epsilon_0` is the permittivity of free space in SI units).
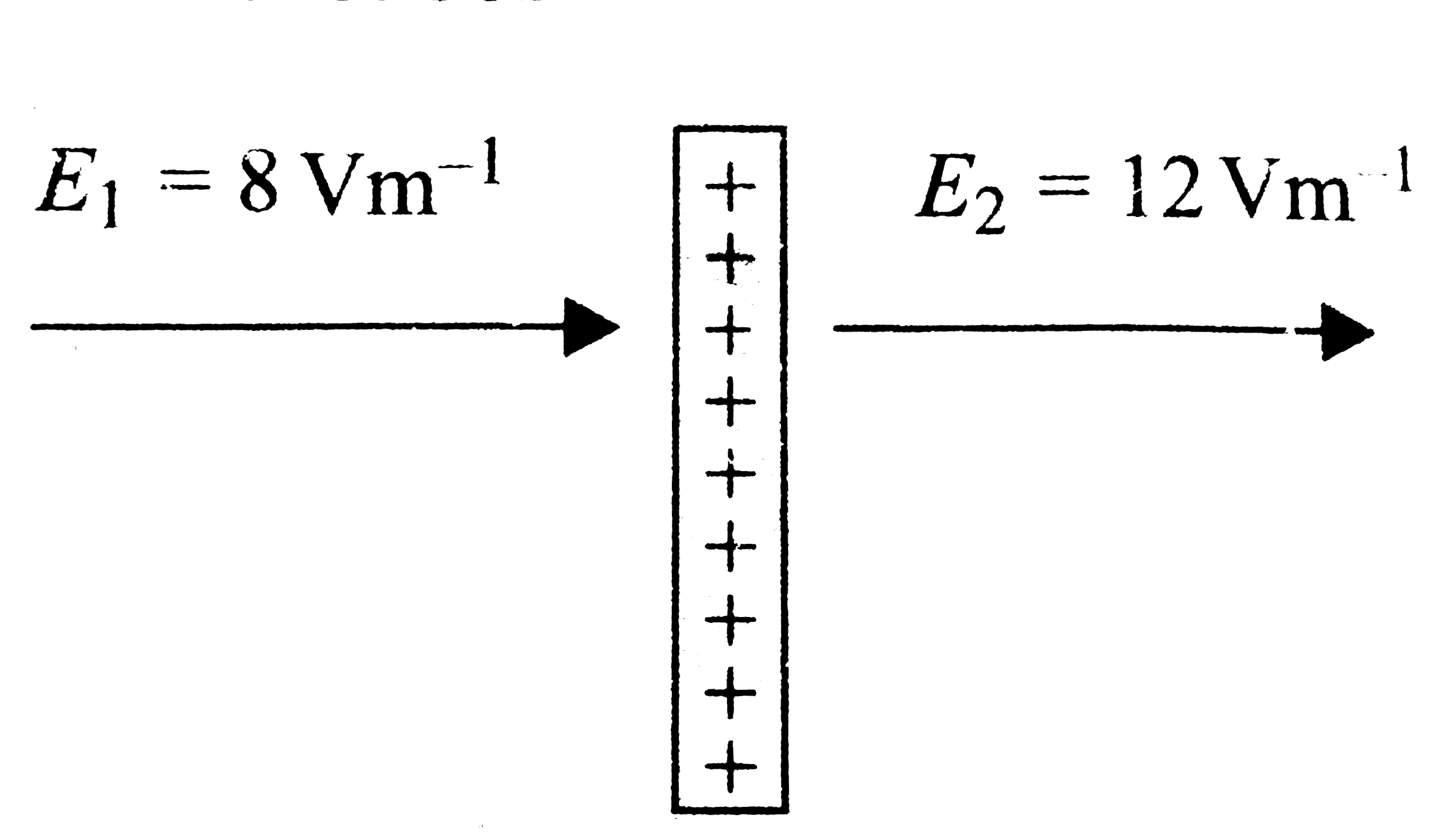
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of `R//2` from the centre?
View SolutionAn uncharged conducting large plate is placed as shown. Now an electric field E towards right is applied. Find the induced charge density on the right surface of the plate.

View SolutionAn uncharge aluminium block has a cavity within it. The block is placed in a region where a uniform electric field is directed upward. Which of the following is a correct statement descrining conditions in the interior of the block's cavity?
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density `rho`. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder is removed.

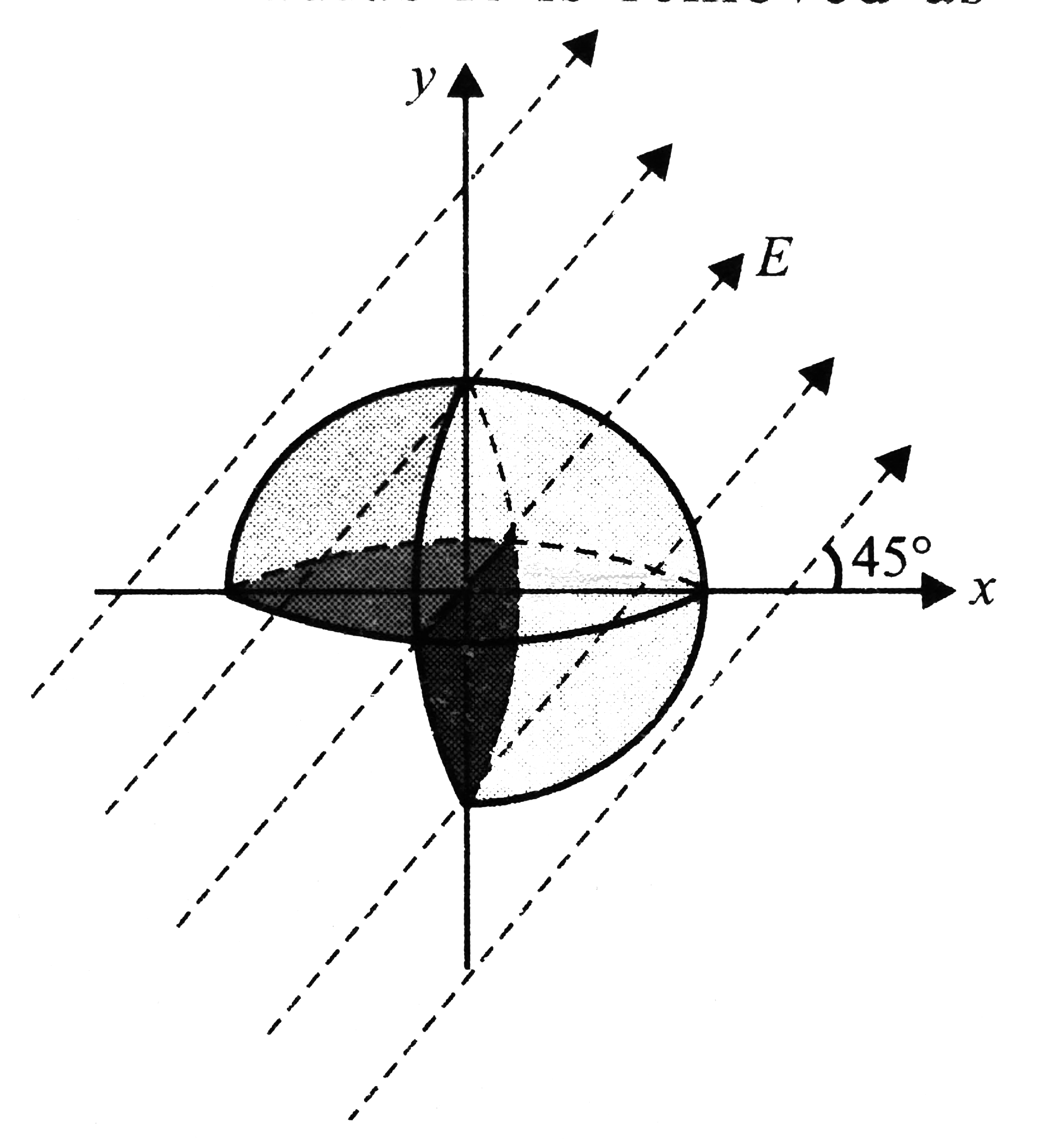
View SolutionOne-fourth of a sphere of radius R is removed as shown in figure. An electric field E exists parallel to the xy plane . Find the flux through the remaining curved part.
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density `-rho`. The center of this sphere is displaced from the origin by `vecd`. The electric field `vecE` at any point P having position vector inside the sphere is

View SolutionA large charged metal sheet is placed in a uniform electric field, perpendicular to the electric field lines. After placing the sheet into the field, the electric field on the left side of the sheet is `E_1 = 5 xx 10^5 Vm^(-1)` and on the right it is `E_2 = 3 xx 10^5 V m^(-1)`. The sheet experiences a net electric force of 0.08 N. Find the area of one face of the sheet. Assume the external field to remain constant after introducing the large sheet. Use
`(1/(4piepsilon_0)) = 9 xx 10^(9) Nm^(2)C^(-2)`

View SolutionA positively charge sphere of radius `r_0` carries a volume charge density `rho`. A spherical cavity of radius `r_0//2` is then scooped out and left empty. `C_1` is the center of the sphere and `C_2` that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionFour very large metal plates are given charges as shown in figure. The middle two are then connected through a wire. Find the charge that will flow through the wire.

View SolutionA conic surface is placed in a uniform electric field E as shown in figure. Such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is `theta`.

Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux `(thetalt45^@)`.
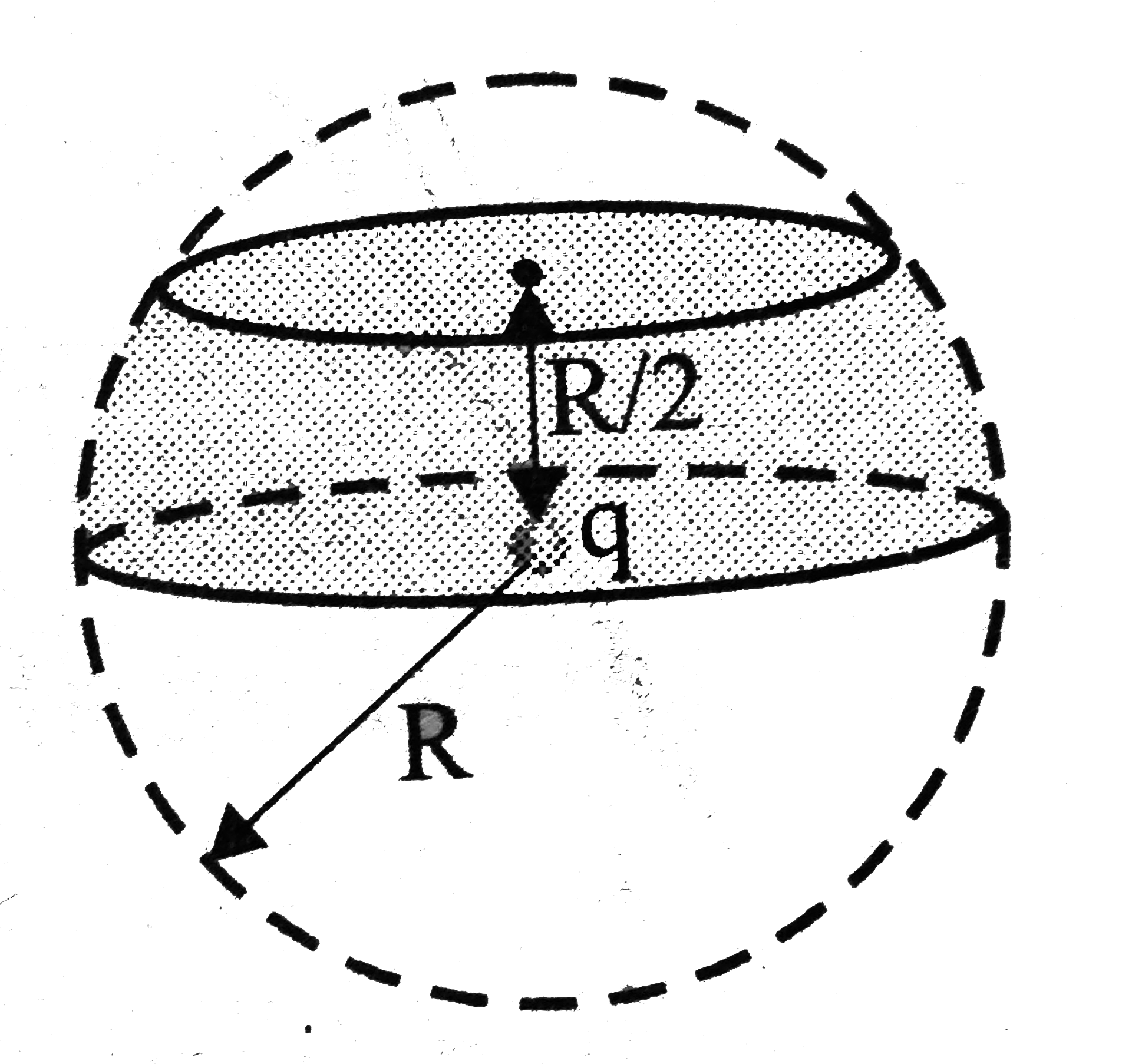
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
View SolutionAn infinitely long line charge having a uniform charge per unit length `lambda` lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where `Rltd` and `Rgtd`.

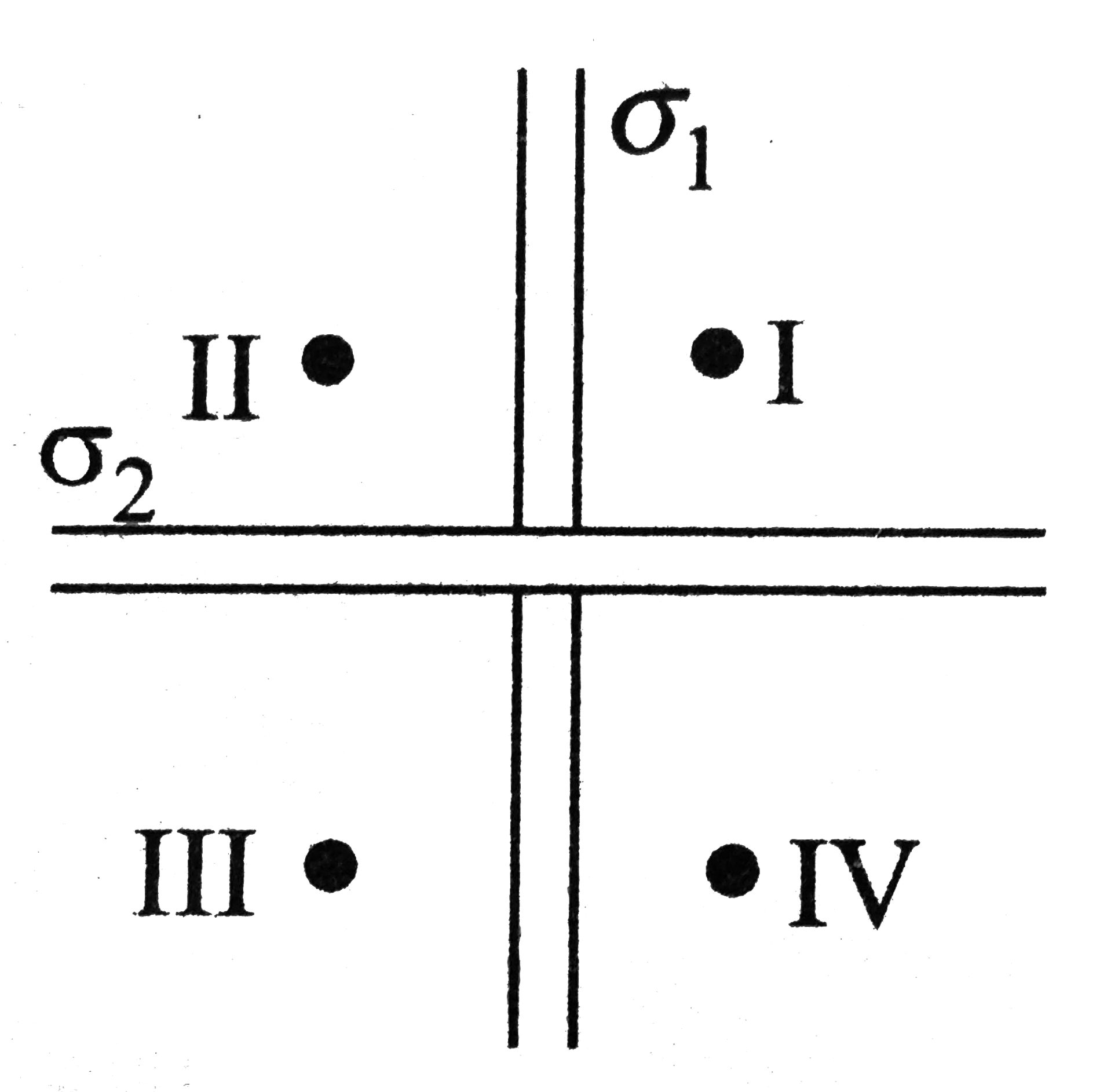
View SolutionTwo infinite sheets having charge densities `sigma_1` and `sigma_2` are placed in two perpendicular planes whose two-dimensional view is shown in figure. The charges are distributed uniformly on the sheets in electrostatic equilibrium condition. Four points are marked I, II, III and IV. The electric field intensities at these points are `vecE_1, vecE_2, vecE_3, and vecE_4`, respectively. The correct expression for the electric field intensities is
View SolutionTwo nonconducting infinite planes sheets having charges Q and 2Q are placed parallel to each other as shown in figure. The charge distribution on the four faces of the two plates is also shown. The electric field intensities at three points 1, 2, and 3 are `vecE_1, vecE_2, and vecE_3`, respectively. Then the magnitudes of `vecE_1 , vecE_2, and vecE_3` are, respectively (surface area of plates is `S` ) :

View SolutionThree large identical conducting parallel plates carrying charge `+Q , -Q, and +2Q`, respectively, are placed as shown in figure. If `E_A, E_b, and E_C` refer to the magnitudes of the electric field at points A, B, and C, respectively. Then
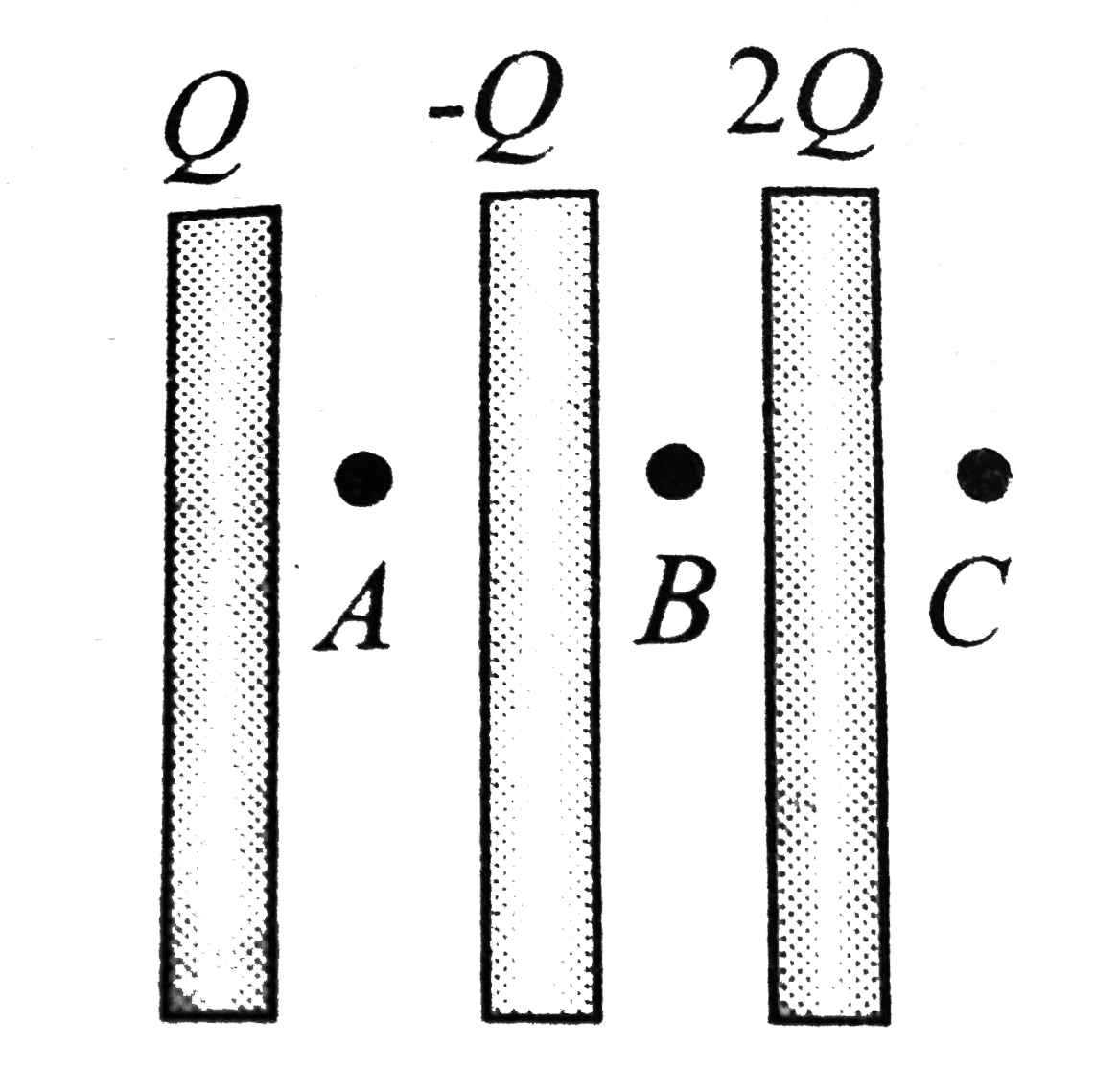
View SolutionThe number of electric field lines crossing an area `DeltaS is n_1 when Delta vecS||vecE`, while the number of field lines crossing the same area is `n_2` when `DeltavecE` makes an angles of `30^@` with `vecE`. Then
View Solution
Single Correct questions and complete solutions for chapter ELECTRIC FLUX AND GAUSS LAW of CENGAGE PHYSICS (HINGLISH) of Class 12