Complete Solutions to Integer of chapter MISCELLANEOUS VOLUME 5 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MISCELLANEOUS VOLUME 5 |
| CENGAGE PHYSICS | Integer |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
A charged particle enters a uniform magnetic field with velocity `v_(0) = 4 m//s` perpendicular to it, the length of magnetic field is `x = ((sqrt(3))/(2)) R`, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View SolutionA charged particle of mass m = 1 mg and charge `q = 1 (mu) C` enter along AB at point A in a uniform magnetic field B = 1.2 T existing in the rectangular region of size `a xx b`, where a = 4 m and b = 3 m. The particle leaves the region exactly at corner point C. What is the speed `v (in m s^(-1))` of the particle?
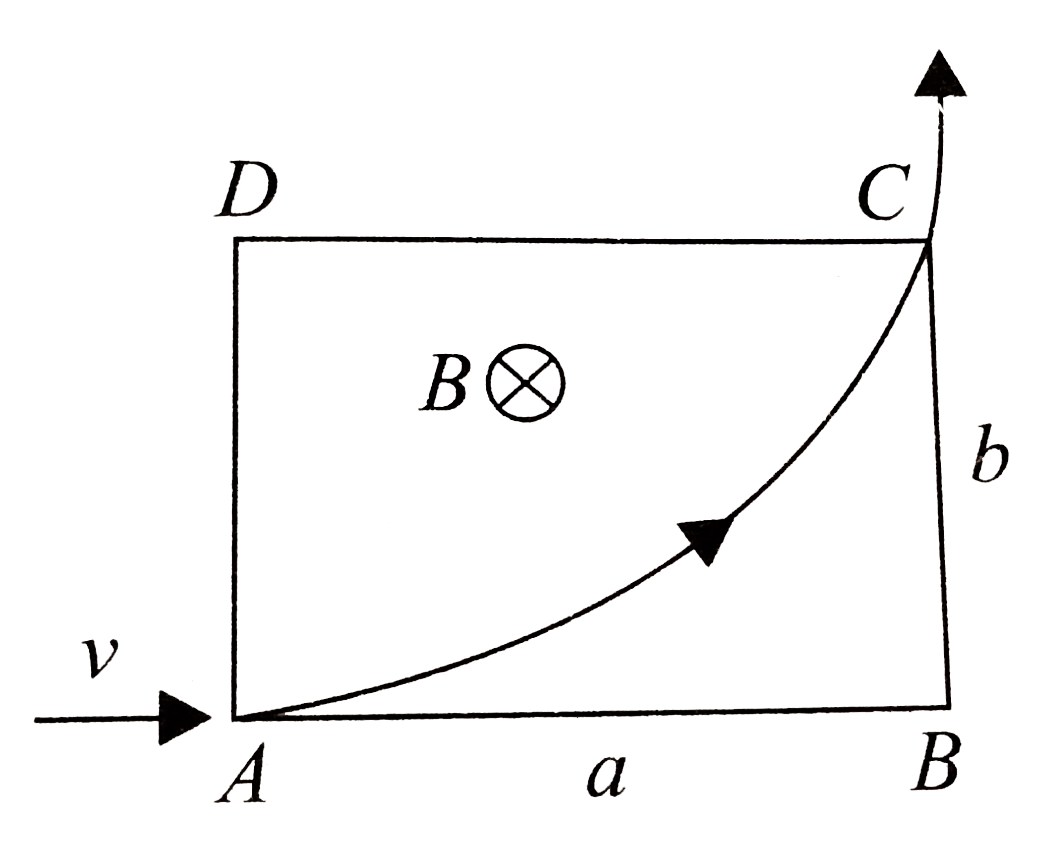
View SolutionTwo parallel wires carrying equal currents `i_(1)` and `i_(2)` with `i_(1)gti_(2)`. When the current are in the same direction, the `10 mT`. If the direction of `i_(2)` is reversed, the field becomes `30 mT`. The ratio `i_(1)//i_(2)` is
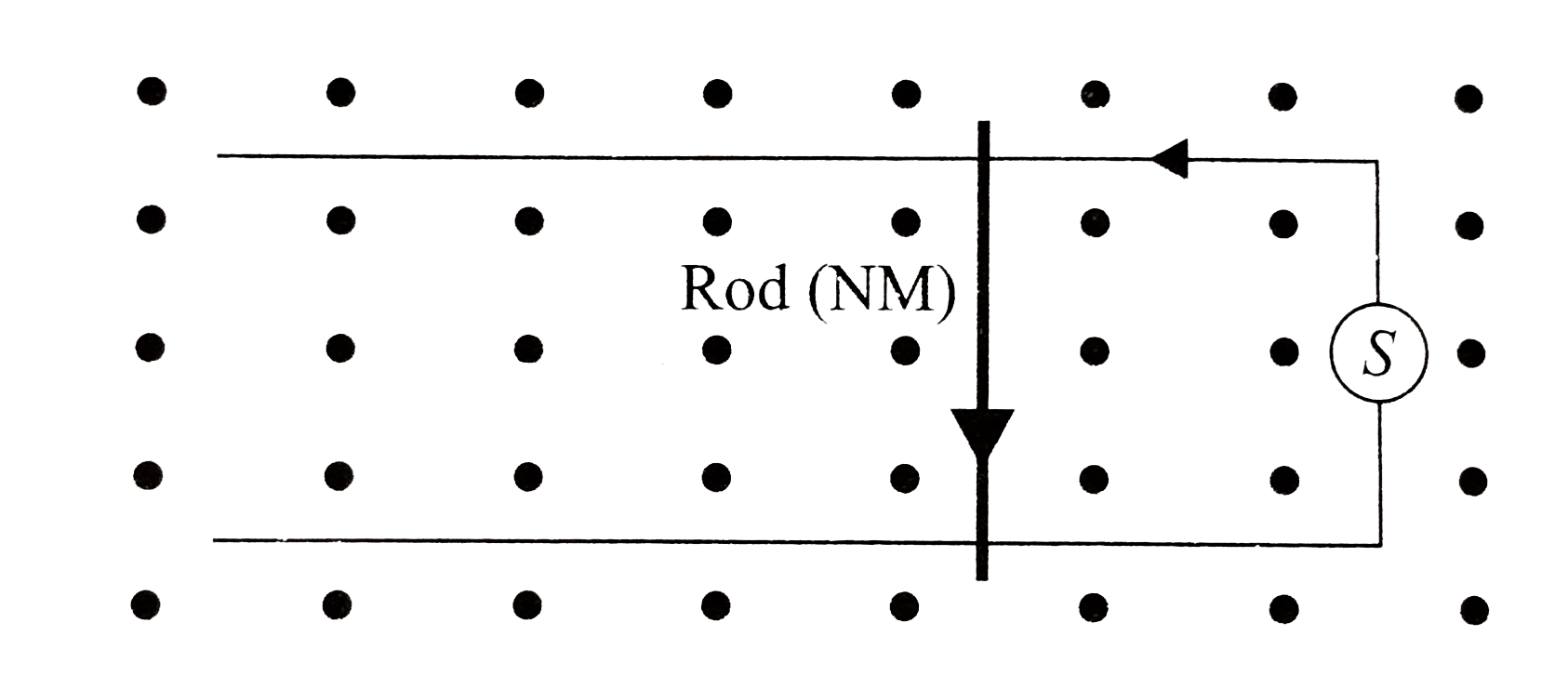
View SolutionA conducting rod of mass 200 gm and length 10 cm can slide without friction on two long, horizontal rails. A uniform magnetic field of magnitude 5 m T exists in the region as shown. A source S is used to maintain a constant current 2 A through the rod. If motion of the rod starts from the rest, find its speed (in cm/s) after 10 s from the start of the motion
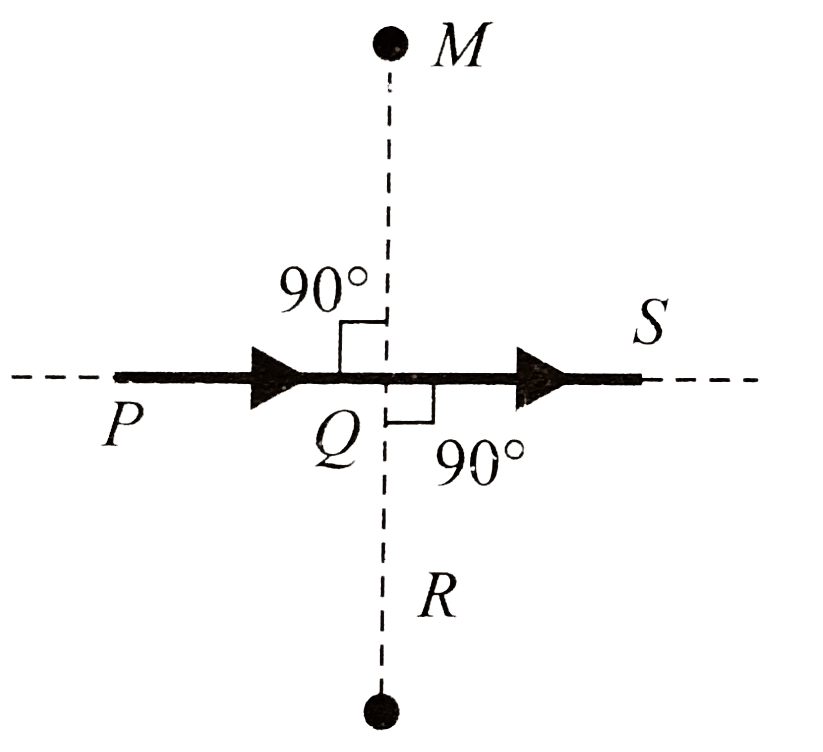
View SolutionAn infinitely long conductor PQR is bent to form a right angle as shown. A current I flows through PQR. The magnetic field due to this current at the point `M is B_(1)`. Now, another infinitely long straight conductor QS is connected at Q so that the current is `I//2` in QR as well as in QS, the current in PQ remaining unchanged. The magnetic field at M is now `B_(2) = 4 mT`. Find the value of `B_(1) ("in" mT)`.
View SolutionA magnetic field `vec(B)=-B_(0)hat(i)` exists within a sphere of radius `R=v_(0)Tsqrt(3)` where T is the time period of one revolution of a charged particle starting its motion form origin and moving with a velocity `vce(v)_(0) = (v_0)/(2) sqrt(3) hat(i) - v_(0)/(2) hat(j)`. Find the number of turns that the particle will take to come out of the magnetic field.
View SolutionIn the given circuit, what is the current I (in A) drawn from battery at time t = 0.
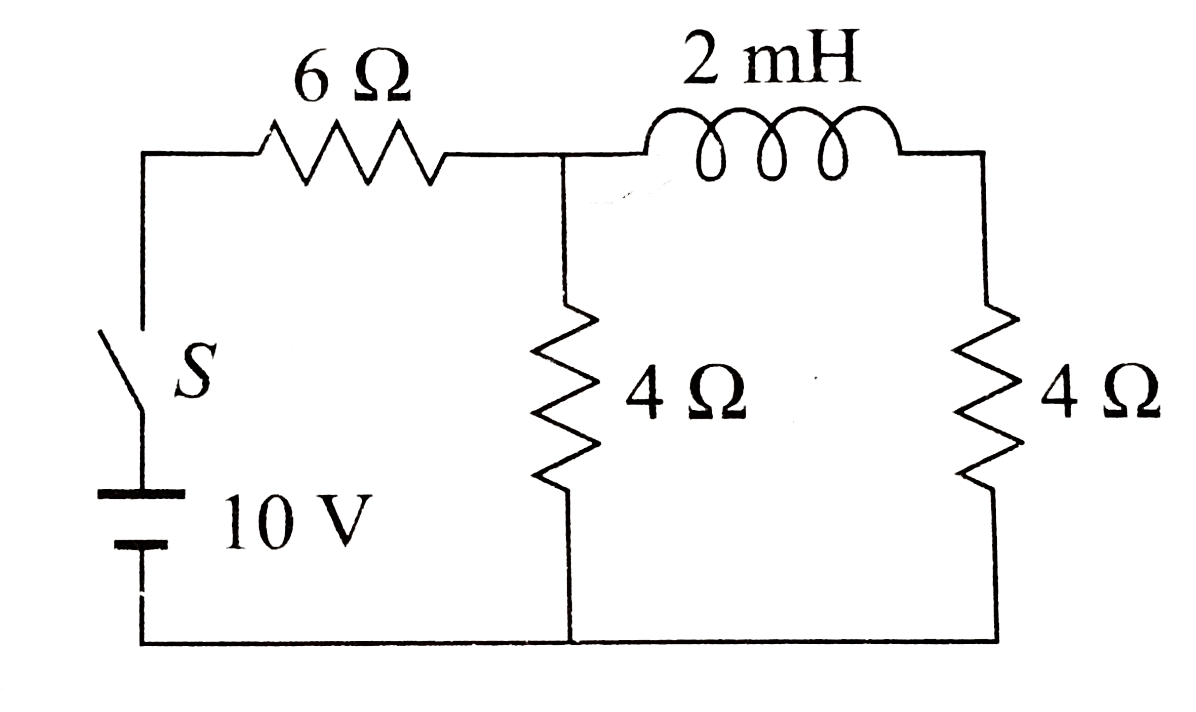
View SolutionA coil of inductance `L = 5//8 H` and of resistance `R = 62.8 (Omega)` is connected to the mains alternating voltage of frequency 50 Hz. What can be the capacitance of the capacitor `(in (mu)F)` connected in series with the coil if the power dissipated has to remain unchanged? Take `(pi)^(2) = 10`.
View SolutionIn the given LCR series circuit find the reading (in A) of the hot wire ammeter. (there all hot wire meters are ideal)
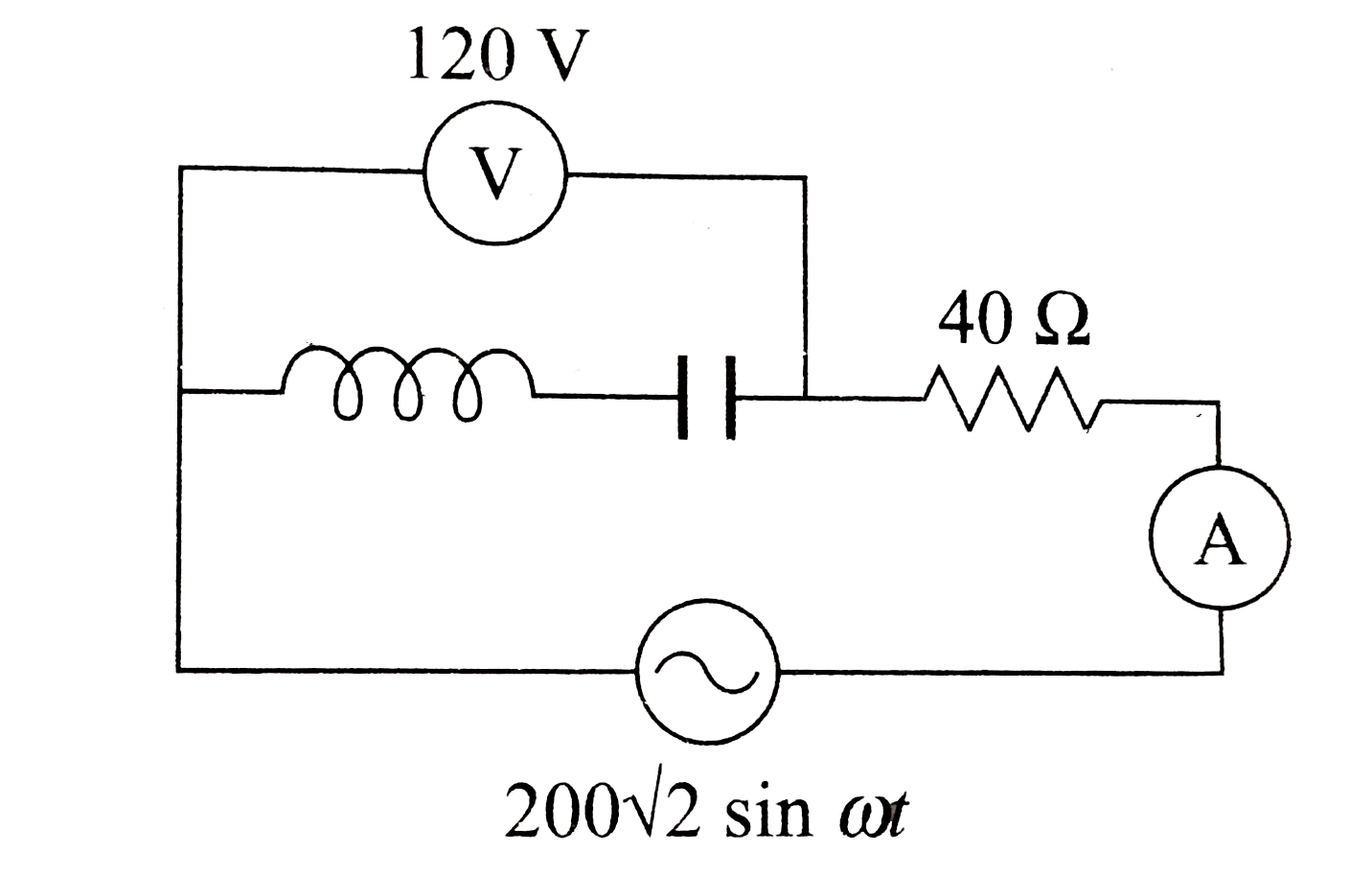
View SolutionAt any instant a current of 2 A is increasing at a rate of `1 A//s` through a coil of indcutance 2 H. Find the energy (in SI units) being stored in the inductor per unit time at that instant.
View SolutionThe diagram shows a circuit having a coil of resistance `R = 2.5 (Omega)` and inductance L connected to a conducting rod PQ which can slide on perfectly conducting circular ring of radius 10 cm with its centre at 'P'. Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exist as shown in Fig.
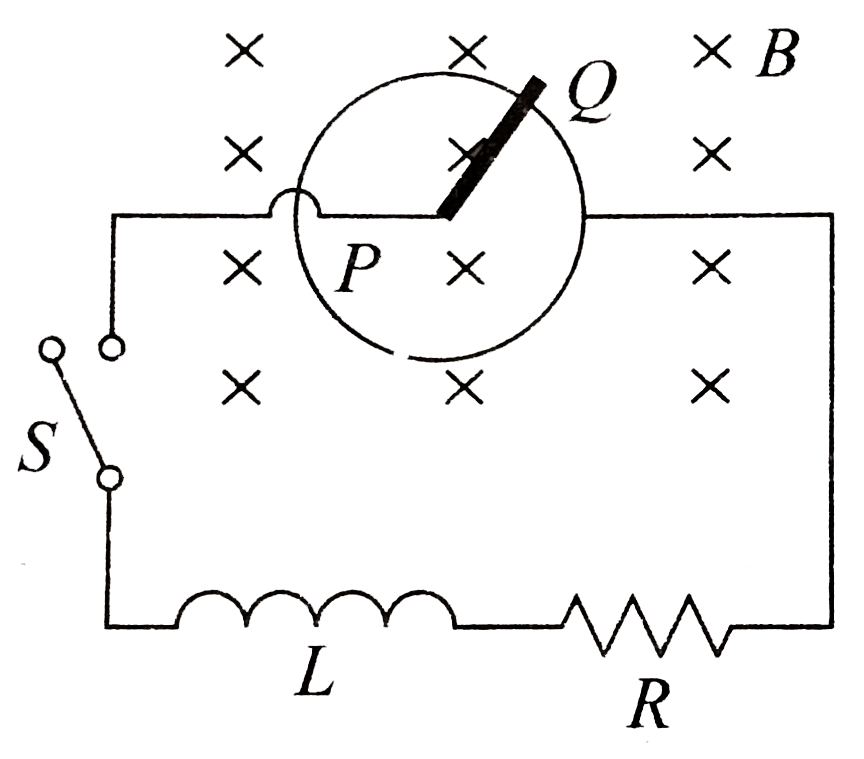
At t = 0, the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity `40 rad//s`. Find magnitude of this torque (in milli Nm) when current reaches half of its maximum value. Neglect the self-inductance of the loop formed by the circuit.
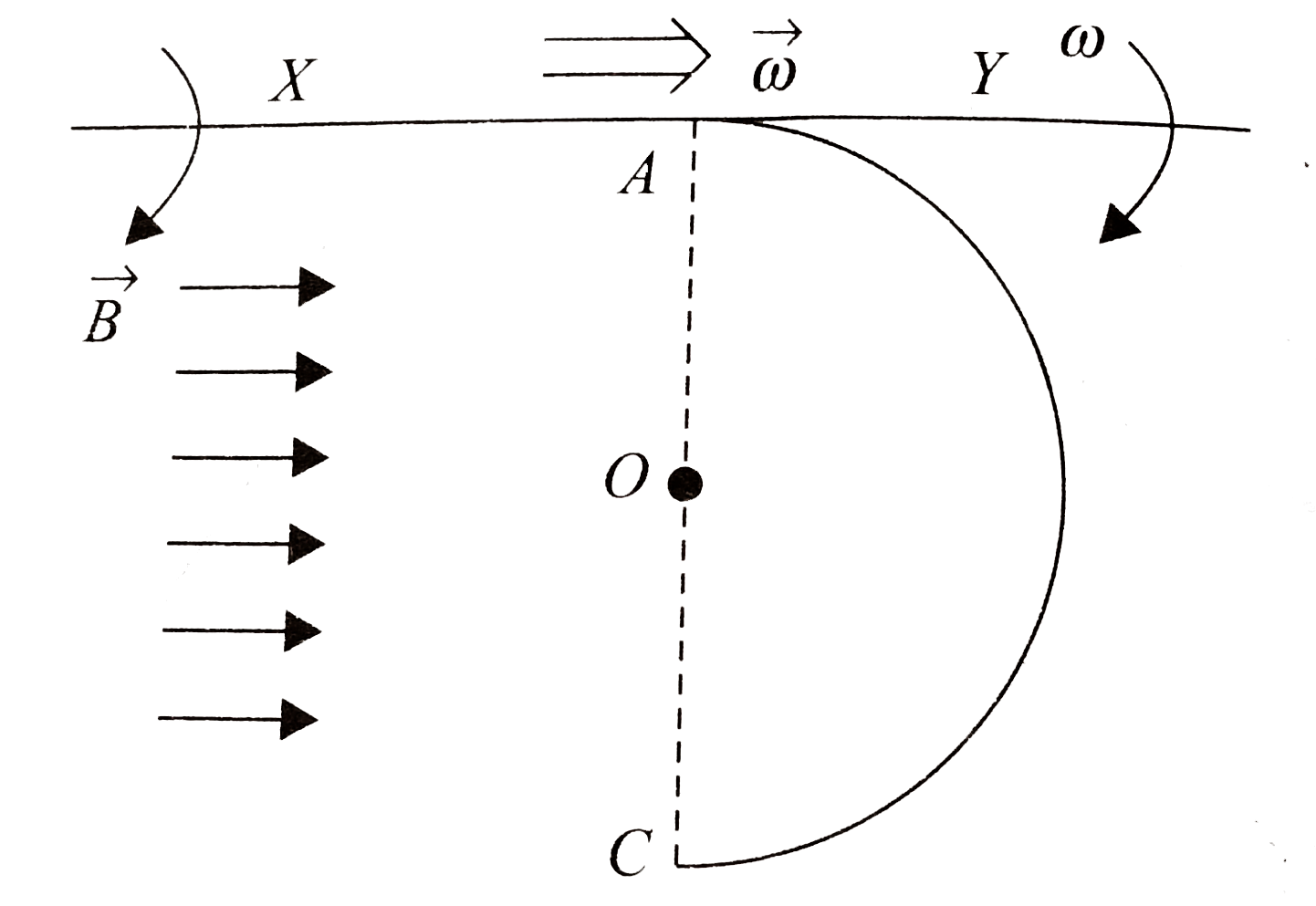
View SolutionA thin wire AC shaped as a semi-circle of diameter d rotates with a constant angular frequency `(omega)` in a uniform magnetic field of indcution `vec(B)`. The vector `vec(omega)` is parallel to `vec(B)` and the rotation axis XY passes through the end A of the wire and is perpendicular to the diameter AC (see Fig.). `vec(B)` is directed left to right in the plane of the paper. The value of the line intergral `I=int vec(E)* d vec(r)` taken along the wire form the point A to the point C will be `(omega Bd^(2))/(?)`. What interger should be inserted in place of question mark.
View Solution
Integer questions and complete solutions for chapter MISCELLANEOUS VOLUME 5 of CENGAGE PHYSICS (HINGLISH) of Class 12