Complete Solutions to EXAMINATION ARCHIVE (WBJEE) of chapter ELECTRIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC FIELD |
| CHHAYA PRAKASHINI | EXAMINATION ARCHIVE (WBJEE) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
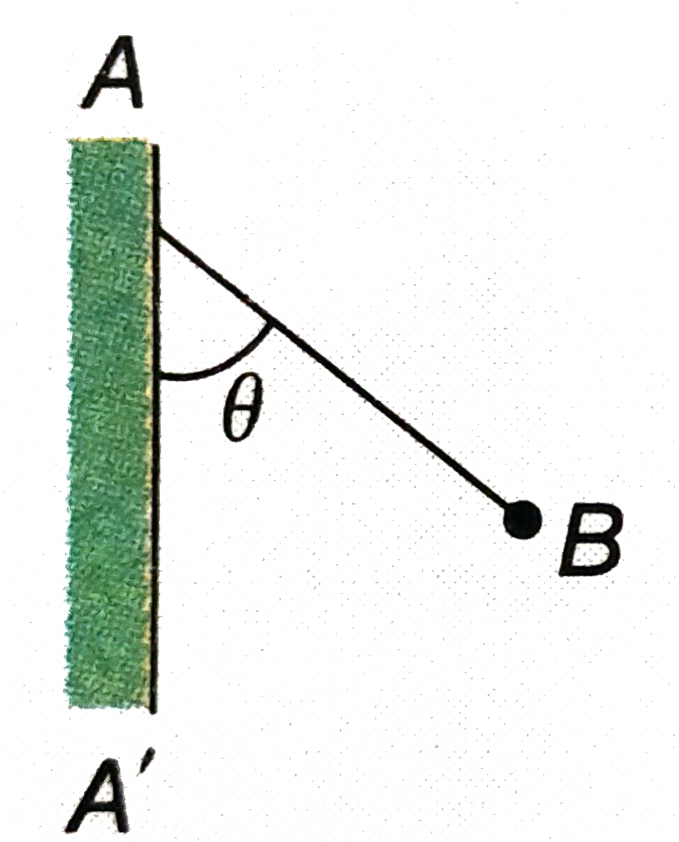
A line AA' is on a charged infinite conducting plane which is perpendicular to the plane of the paper. The plane has a surface density of charge `sigma` and B is a ball of mass m with a like charge of magnitude q.B is connected by a string from a point on the line AA'. The tangent of the angle `(theta)` formed between the line AA' and the string is
View SolutionA charge q is placed at one corner of cube. The elctric flux through any of the three faces adjacent of the charge is zero.
The flux through any one of the other three faces is
View SolutionTwo charges `+q and-q` are placed at a distance a in a uniform electric field. The dipole moment of the combination is `2aq(cos theta hati+ sin theta hatj)`, where `theta` is the angle between the direction of the field and the line joining the two charges. which of the following statement (s) is/are correct ?
View SolutionA charged particle of mass `m_(1) ` and charge `q_(1)` is revolving in a cricle of radius r. another charged particle of charge `q_(2)` and mass `m_(2)` is situated at the centre of the circle. If the velocity and time period of the revolving particle be v and T respectively, then,
View SolutionA Current `I= I_(0) e^(- lambdat)` is flowing in a circuit consisiting of a parallel combination of resistance R and capacitance C.
The total charge over the entire pulse period is
View SolutionA positive charge Q is situated at the centre of cube. The electric flux through any face of the cube is (in SI units)
View SolutionA charge of `0.8C` is divided into two charges `Q_(1) and Q_(2)`. These are kept at a separation of 30 cm. The force on `Q_(1)` is maximum when
View SolutionA particle with charge QC, tied at the end of an inextensible string of length R metre, revolves in a vertical plane. At the centre of the circular trajectory there is a fxied charge of magnitude QC. The mass of the moving charge M is such that `Mg=(Q^(2))/(4pi epsi_(0)R^(2))` . If at the highest position of the particle, the tenstion of the string just vanishes, the horizontal velocity at the lowest point has to be
View SolutionA particle with charge e and mass m, moving along the X-axis with a uniform speed u enters a region where a uniform electric field E is acting along the Y-axis. The particle starts to move in a parabola. Its focal length (neglecting any effect of gravity) is
View SolutionA unit negative charge with mass resides at the midpoint of the straight line of length 2a adjoining two fixed charges of magnitude `+Q` each. If it is given a very small displacement `x(x lt lt a)` in a direction perpendicular to the straight line, it will
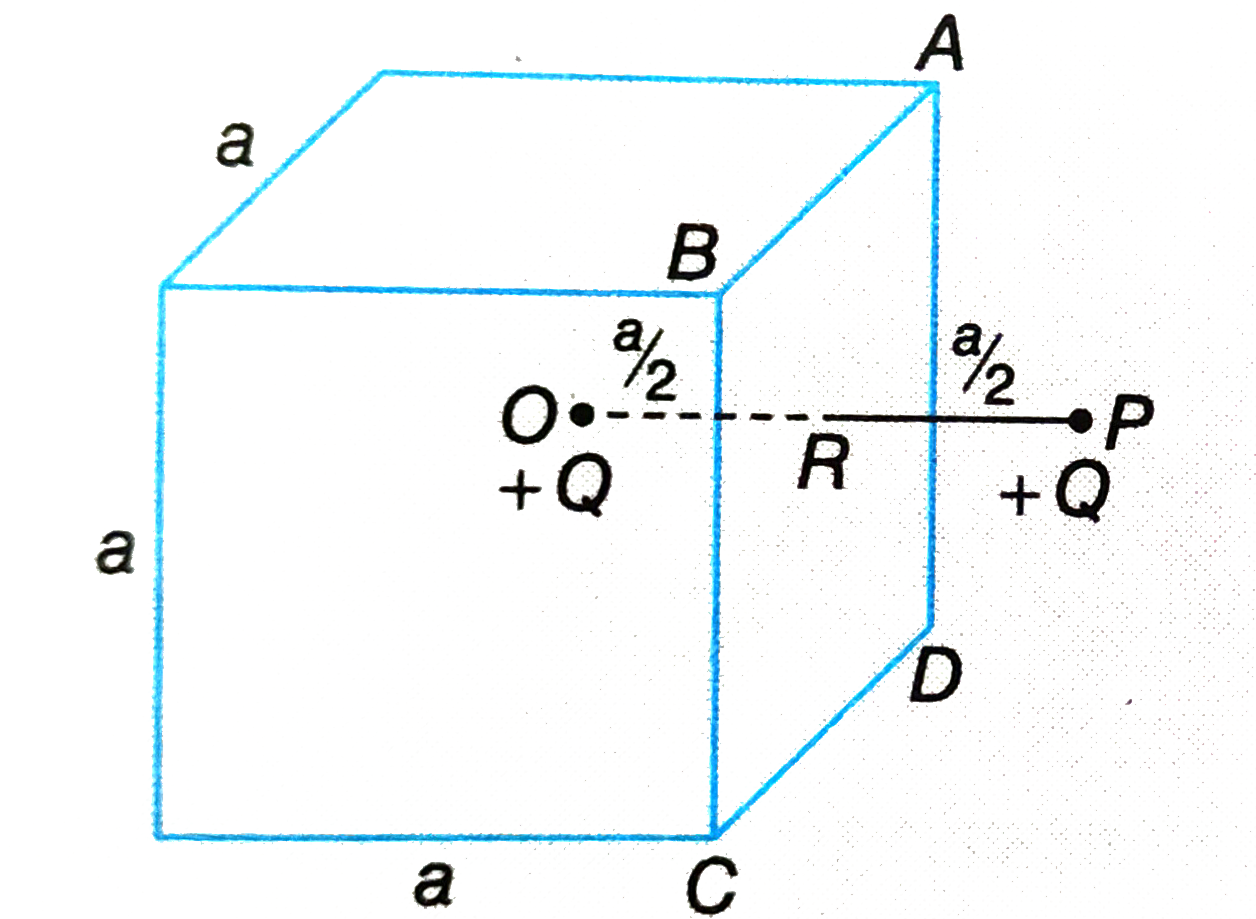
View SolutionConsider a region in free space bounded by the surfaces of an imaginary cube having sides of length a as shown in the diagram. A charge +Q is placed at the centre O of the cube. P is such a point outside the cube that the line OP perpendicularly intersects the surface ABCD at R and also `OR=RP=(a)/(2)`. A charge +Q is placed at point P also. What is the total electrie flux through the five faces of the cube other than ABCD?
View SolutionFour equal charges of value +Q are placed at any four vertices of a regular hexagon of side a. By suitably choosing the vertices, what can be the maximum possible magnitude of electric field at the centre of the hexagon?
(A) `(Q)/(4piin_(0)a^(2))`
(B) `(sqrt2Q)/(4piin_(0)a^(2))`
(C) `(sqrt3Q)/(4piin_(0)a^(2))`
(D) `(2Q)/(4piin_(0)a^(2))`
View SolutionThe bob of a pendulum of mass m, suspended by an inextensible string of length L as shown in the figure carries a small charge q. An infinite horizonatal plane conductor with uniform surface charge density `sigma` is placed below it. What will be the time period of the pendulum for small amplitude oscillations?

View Solution
EXAMINATION ARCHIVE (WBJEE) questions and complete solutions for chapter ELECTRIC FIELD of CHHAYA PHYSICS (BENGALI ENGLISH) of Class 12
All Exercises from CHHAYA PRAKASHINI Class 12 PHYSICS ELECTRIC FIELD
- CBSE SCANNER
- ENTRACNCE CORNER ( COMPREHENSION TYPE )
- ENTRACNCE CORNER ( INTEGER ANSWER TYPE )
- ENTRACNCE CORNER (ASSERTION-REASON TYPE )
- ENTRACNCE CORNER (MULTIPLE CORRECT ANSWER TYPE )
- EXAMINATION ARCHIVE ( AIPMT)
- EXAMINATION ARCHIVE ( JEE MAIN )
- EXAMINATION ARCHIVE ( NEET )
- EXAMINATION ARCHIVE (WBCHSE)
- EXAMINATION ARCHIVE (WBJEE)
- EXERCISE ( HOTS NUMERICAL PROBLEMS )
- EXERCISE ( MULTIPLE CHOICE QUESTION )
- EXERCISE ( VERY SHORT ANSWER TYPE QUESTIONS )
- EXERCISE (PROBLEM SET -I)
- EXERCISE (PROBLEM SET -II)
- EXERCISE (SHORT ANSWER TYPE QUESTIONS-I )
- EXERCISE (SHORT ANSWER TYPE QUESTIONS-II )
- HIGHER ORDER THINKING SKILL QUESTIONS
- NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT
- NCERT TEXTBOOK QUESTIONS WITH ANSWER HINT
- NUMERICAL EXAMPLES
- SECTION RELATION QUESTIONS